机器学习深度学习——自注意力和位置编码(数学推导+代码实现)
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er
🌌上期文章:机器学习&&深度学习——注意力分数(详细数学推导+代码实现)
📚订阅专栏:机器学习&&深度学习
希望文章对你们有所帮助
自注意力和位置编码
- 引入
- 自注意力
- 多头注意力
- 基于多头注意力实现自注意力
- 比较CNN、RNN和self-attention
- 结论
- 剖析——CNN
- 剖析——RNN
- 剖析——self-attention
- 总结
- 位置编码
- 绝对位置信息
- 相对位置信息
- 小结
引入
在深度学习中,经常使用CNN和RNN对序列进行编码。有了自注意力之后,我们将词元序列输入注意力池化中,以便同一组词元同时充当查询、键和值。具体来说,每个查询都会关注所有的键-值对并生成一个注意力输出。由于查询、键和值来自同一组输入,因此被称为自注意力(self-attention)。下面将使用自注意力进行序列编码。
import math
import torch
from torch import nn
from d2l import torch as d2l
自注意力
给定一个由词元组成的序列:
x 1 , . . . , x n 其中任意 x i ∈ R d x_1,...,x_n\\ 其中任意x_i∈R^d x1,...,xn其中任意xi∈Rd
该序列的自注意力输出为一个长度相同的序列:
y 1 , . . . , y n 其中 y i = f ( x i , ( x 1 , x 1 ) , . . . , ( x n , x n ) ) ∈ R d y_1,...,y_n\\ 其中y_i=f(x_i,(x_1,x_1),...,(x_n,x_n))∈R^d y1,...,yn其中yi=f(xi,(x1,x1),...,(xn,xn))∈Rd
自注意力就是这样,任意的xi都是既当key,又当value,还当query。
下面的代码片段是基于多头注意力对一个张量完成自注意力的计算,张量形状为(批量大小,时间步数目或词元序列长度,d)。输出与输入的张量形状相同。
而在此之前,简单讲解下多头注意力,接着基于多头注意力实现自注意力。
多头注意力
当给定相同的查询、键和值的集合时,我们希望模型可以基于相同的注意力机制学习到不同的行为,然后将不同的行为作为知识组合起来,捕获序列内各种范围的依赖关系。因此允许注意力机制组合使用查询、键和值的不同子空间表示是有益的。
因此,与其只使用一个注意力池化,我们可以独立学习得到h组不同的线性投影来变换查询、键和值。然后,这h组变换后的查询、键和值将并行地送到注意力池化中。最后将这h个注意力池化的输出拼接在一起,并通过另一可以学习的线性投影进行变换,来产生最终输出。这就是多头注意力(multihead attention),如下图所示:
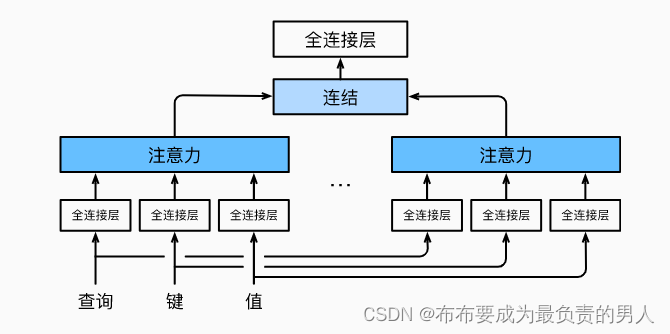
而多头注意力的实现过程通常使用的是缩放点积注意力来作为每一个注意力头,我们设定:
p q = p k = p v = p o / h p_q=p_k=p_v=p_o/h pq=pk=pv=po/h
值得注意的是,如果将查询、键和值的线性变化的输出数量设置为:
p q h = p k h = p v h = p o p_qh=p_kh=p_vh=p_o pqh=pkh=pvh=po
就可以并行计算h个头,下面代码中的po是通过num_hiddens指定的。
代码如下:
#@save
class MultiHeadAttention(nn.Module):"""多头注意力"""def __init__(self, key_size, query_size, value_size, num_hiddens,num_heads, dropout, bias=False, **kwargs):super(MultiHeadAttention, self).__init__(**kwargs)self.num_heads = num_headsself.attention = d2l.DotProductAttention(dropout)self.W_q = nn.Linear(query_size, num_hiddens, bias=bias)self.W_k = nn.Linear(key_size, num_hiddens, bias=bias)self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias)def forward(self, queries, keys, values, valid_lens):# queries,keys,values的形状:# (batch_size,查询或者“键-值”对的个数,num_hiddens)# valid_lens 的形状:# (batch_size,)或(batch_size,查询的个数)# 经过变换后,输出的queries,keys,values 的形状:# (batch_size*num_heads,查询或者“键-值”对的个数,# num_hiddens/num_heads)queries = transpose_qkv(self.W_q(queries), self.num_heads)keys = transpose_qkv(self.W_k(keys), self.num_heads)values = transpose_qkv(self.W_v(values), self.num_heads)if valid_lens is not None:# 在轴0,将第一项(标量或者矢量)复制num_heads次,# 然后如此复制第二项,然后诸如此类。valid_lens = torch.repeat_interleave(valid_lens, repeats=self.num_heads, dim=0)# output的形状:(batch_size*num_heads,查询的个数,# num_hiddens/num_heads)output = self.attention(queries, keys, values, valid_lens)# output_concat的形状:(batch_size,查询的个数,num_hiddens)output_concat = transpose_output(output, self.num_heads)return self.W_o(output_concat)#@save
def transpose_qkv(X, num_heads):"""为了多注意力头的并行计算而变换形状"""# 输入X的形状:(batch_size,查询或者“键-值”对的个数,num_hiddens)# 输出X的形状:(batch_size,查询或者“键-值”对的个数,num_heads,# num_hiddens/num_heads)X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)# 输出X的形状:(batch_size,num_heads,查询或者“键-值”对的个数,# num_hiddens/num_heads)X = X.permute(0, 2, 1, 3)# 最终输出的形状:(batch_size*num_heads,查询或者“键-值”对的个数,# num_hiddens/num_heads)return X.reshape(-1, X.shape[2], X.shape[3])#@save
def transpose_output(X, num_heads):"""逆转transpose_qkv函数的操作"""X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])X = X.permute(0, 2, 1, 3)return X.reshape(X.shape[0], X.shape[1], -1)
基于多头注意力实现自注意力
num_hiddens, num_heads = 100, 5
attention = d2l.MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens,num_hiddens, num_heads, 0.5)
attention.eval()
可以输出验证一下:
batch_size, num_queries, valid_lens = 2, 4, torch.tensor([3, 2])
X = torch.ones((batch_size, num_queries, num_hiddens))
print(attention(X, X, X, valid_lens).shape)
输出结果:
torch.Size([2, 4, 100])
比较CNN、RNN和self-attention
首先看这个图:
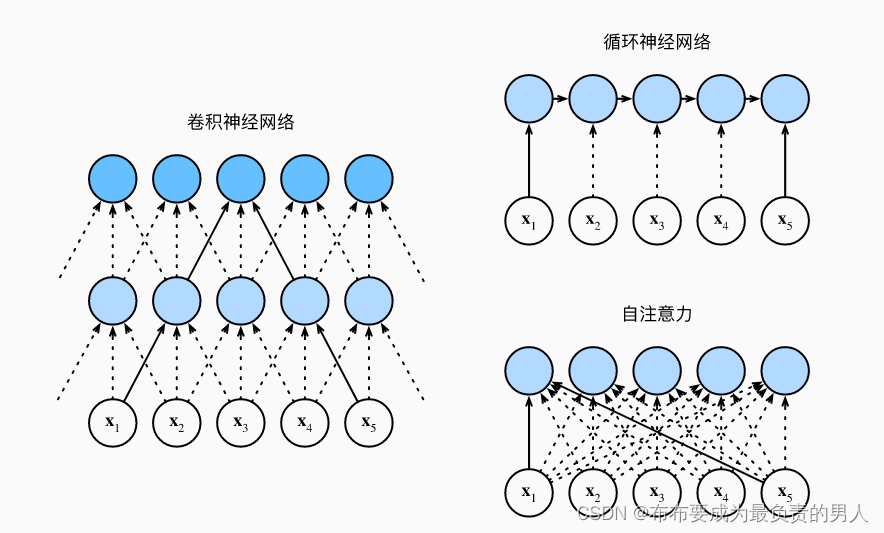
接下来进行CNN、RNN以及self-attention三个架构的比较,首先这三个架构目标都是要将n个词元组成的序列映射到另一个长度相同的序列,其中的每个输入词元或输出词元都由d维向量表示。我们的比较将基于计算的复杂性、顺序操作和最大路径长度,先给出结论再进行剖析解释。
我们首先要知道,顺序操作会妨碍并行计算,而任意的序列位置组合之间的路径越短,则能更轻松地学习序列中的远距离依赖关系。
结论
| 计算复杂度 | 并行度 | 最大路径长度 | |
|---|---|---|---|
| CNN | O(knd2) | O(n) | O(n/k) |
| RNN | O(nd2) | O(1) | O(n) |
| self-attention | O(n2d) | O(n) | O(1) |
剖析——CNN
考虑一个卷积核大小为k的卷积层,由于序列长度是n,输入和输出的通道数量都是d,所以卷积层的计算复杂度为O(knd2)。而如上图所示,可以看出CNN网络是分层的,因此会有O(1)个顺序操作,那么这代表着通道可以并行执行n个词元,那么并行度就是O(n)。
上图中可以看出k=3,因为这样刚好就使得x1和x5处于这个卷积核大小为3的双层卷积神经网络的感受野内。因此最大的路径长度一定是不会超过n/k的,下标为n的也会因为卷积核被限制到一个感受野内,因此可以知道最大路径长度为O(n/k)。
剖析——RNN
当更新RNN的隐状态时,d×d权重矩阵和d维隐状态的乘法计算复杂度为O(d2),再加上序列长度为n,因此RNN的计算复杂度为O(nd2),由上图也可以看出n个序列的顺序操作是没办法并行化的,则并行度为O(1),最大路径长度是O(n)(可以理解成当我们要组合y1和yn的时候,这时候长度为n)。
剖析——self-attention
查询、键、值都是n×d矩阵。计算过程为:n×d矩阵乘以d×n矩阵,之后得到的n×n矩阵再乘以n×d矩阵,因此自注意力有O(n2d)的计算复杂度。而上图展示了自注意力的强大,O(n)的并行度显而易见,同时最大路径长度是O(1),因为他们可以任意组合。
总结
总而言之,卷积神经网络和自注意力都拥有并行计算的优势,而且自注意力的最大路径长度最短。
但是因为其计算复杂度是关于序列长度的二次方,所以在很长的序列中计算会非常慢。
位置编码
在处理词元序列时,循环神经网络是逐个的重复地处理词元的,而自注意力则因为并行计算而放弃了顺序操作。为了使用序列的顺序信息,通过在输入表示中添加位置编码来注入绝对的或相对的位置信息。
位置编码可以通过学习得到也可以直接固定得到,下面讲解基于正弦函数和余弦函数的固定位置编码。
假设输入表示X∈Rn×d包含一个序列中n个词元的d维嵌入表示。位置编码使用相同形状的位置嵌入矩阵P∈Rn×d输出X+P,矩阵第[i,2j](偶数列)和[i,2j+1](奇数列)列上的元素为:
p i , 2 j = s i n ( i 1000 0 2 j / d ) , p i , 2 j + 1 = c o s ( i 1000 0 2 j / d ) p_{i,2j}=sin(\frac{i}{10000^{2j/d}}),\\ p_{i,2j+1}=cos(\frac{i}{10000^{2j/d}}) pi,2j=sin(100002j/di),pi,2j+1=cos(100002j/di)
看起来很奇怪,在后面讲解的时候就能看出来了,先定义一个类来实现它:
#@save
class PositionalEncoding(nn.Module):"""位置编码"""def __init__(self, num_hiddens, dropout, max_len=1000):super(PositionalEncoding, self).__init__()self.dropout = nn.Dropout(dropout)# 创建一个足够长的Pself.P = torch.zeros((1, max_len, num_hiddens))X = torch.arange(max_len, dtype=torch.float32).reshape(-1, 1) / torch.pow(10000, torch.arange(0, num_hiddens, 2, dtype=torch.float32) / num_hiddens)self.P[:, :, 0::2] = torch.sin(X)self.P[:, :, 1::2] = torch.cos(X)def forward(self, X):X = X + self.P[:, :X.shape[1], :].to(X.device)return self.dropout(X)
我们可以进行打印图像,可以清晰看到6、7列比8、9列频率高,而6与7(8与9同理)由于正余弦函数的相位交替,而导致偏移量不同。
encoding_dim, num_steps = 32, 60
pos_encoding = PositionalEncoding(encoding_dim, 0)
pos_encoding.eval()
X = pos_encoding(torch.zeros((1, num_steps, encoding_dim)))
P = pos_encoding.P[:, :X.shape[1], :]
d2l.plot(torch.arange(num_steps), P[0, :, 6:10].T, xlabel='Row (position)',figsize=(6, 2.5), legend=["Col %d" % d for d in torch.arange(6, 10)])
d2l.plt.show()
运行结果:
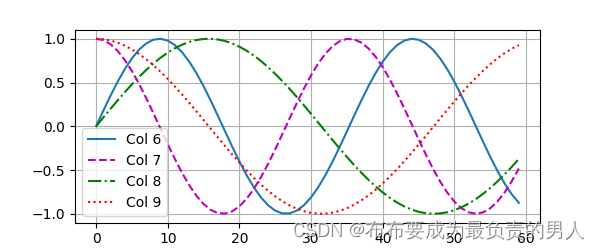
绝对位置信息
其实就是二进制了,想象一下0-7的二进制表示是各不相同的,而且容易知道:较高比特位的交替频率低于较低比特位(而使用三教函数的话输出的是浮点数,显然会更省空间)。
相对位置信息
除了捕获绝对位置信息之外,上述的位置编码还允许模型学习得到输入序列中相对位置信息。这是因为对于任何确定的位置偏移σ,位置i+σ处的位置编码可以线性投影位置i处的位置编码来表示。
用数学来表示:
令 w j = 1 / 1000 0 2 j / d ,对于任何确定的位置偏移 σ : [ c o s ( σ w j ) s i n ( σ w j ) − s i n ( σ w j ) c o s ( σ w j ) ] [ p i , 2 j p i , 2 j + 1 ] = [ c o s ( σ w j ) s i n ( i w j ) + s i n ( σ w j ) c o s ( i w j ) − s i n ( σ w j ) s i n ( i w j ) + c o s ( σ w j ) c o s ( i w j ) ] = [ s i n ( ( i + σ ) w j ) c o s ( ( i + σ ) w j ) ] ——积化和差 = [ p i + σ , 2 j p i + σ , 2 j + 1 ] 令w_j=1/10000^{2j/d},对于任何确定的位置偏移σ:\\ \begin{bmatrix} cos(σw_j)&sin(σw_j)\\ -sin(σw_j)&cos(σw_j) \end{bmatrix} \begin{bmatrix} p_{i,2j}\\ p_{i,2j+1} \end{bmatrix}\\ =\begin{bmatrix} cos(σw_j)sin(iw_j)+sin(σw_j)cos(iw_j)\\ -sin(σw_j)sin(iw_j)+cos(σw_j)cos(iw_j) \end{bmatrix}\\ =\begin{bmatrix} sin((i+σ)w_j)\\ cos((i+σ)w_j) \end{bmatrix}——积化和差\\ =\begin{bmatrix} p_{i+σ,2j}\\ p_{i+σ,2j+1} \end{bmatrix} 令wj=1/100002j/d,对于任何确定的位置偏移σ:[cos(σwj)−sin(σwj)sin(σwj)cos(σwj)][pi,2jpi,2j+1]=[cos(σwj)sin(iwj)+sin(σwj)cos(iwj)−sin(σwj)sin(iwj)+cos(σwj)cos(iwj)]=[sin((i+σ)wj)cos((i+σ)wj)]——积化和差=[pi+σ,2jpi+σ,2j+1]
2×2投影矩阵不依赖于任何位置的索引i。
小结
1、在自注意力中,查询、键和值都来自同一组输入。
2、卷积神经网络和自注意力都拥有并行计算的优势,而且自注意力的最大路径长度最短。但是因为其计算复杂度是关于序列长度的二次方,所以在很长的序列中计算会非常慢。
3、为了使用序列的顺序信息,可以通过在输入表示中添加位置编码,来注入绝对的或相对的位置信息。
相关文章:

机器学习深度学习——自注意力和位置编码(数学推导+代码实现)
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er 🌌上期文章:机器学习&&深度学习——注意力分数(详细数学推导代码实现) 📚订阅专栏:机器学习…...

02.案列项目Demo
1.创建项目 1. 创建项目 用pycharm 选择对应的编译器,输入对应的文件名,点击创建项目。删除默认外层生成的template和DIRS 配置项: 2. 创建App 创建appo1的命令: python manage.py startapp app01 如果使用pycharm>tool>…...

PDF校对:追求文档的精准与完美
随着数字化时代的到来,PDF已经成为了多数机构和个人首选的文件格式,原因在于它的稳定性、跨平台特性以及统一的显示效果。但是,对于任何需要公开或正式发布的文档,确保其内容的准确性是至关重要的,这就是PDF校对显得尤…...
低代码解放生产力,助力企业高效发展
近年来,随着数字化转型的推进,企业对于软件开发的需求日益显著。然而,传统的软件开发模式通常需要耗费大量时间和资源,限制了企业的快速响应能力。为了解决这一难题,低代码开发平台应运而生,成为企业和开发…...

【前端从0开始】CSS——9、浮动
1. 浮动(float) 1.1 定义 float 属性定义元素向哪个方向浮动。之前这个属性应用于图像,使文本围绕在图像周围,不过在 CSS 中,任何元素都可以浮动。浮动元素会生成一个块级框,不论它本身是何种元素。 取值…...
如何在Moonriver网络上向社区代表委托投票权利
我们之前介绍了「社区代表」这一概念,想必大家对社区代表在治理中扮演的角色和地位有了一定的了解。 本文将介绍如何将您的投票权利委托给社区代表。请注意,在委托Token给社区代表这一过程中,并非将您的Token转移给任何人,而且此…...
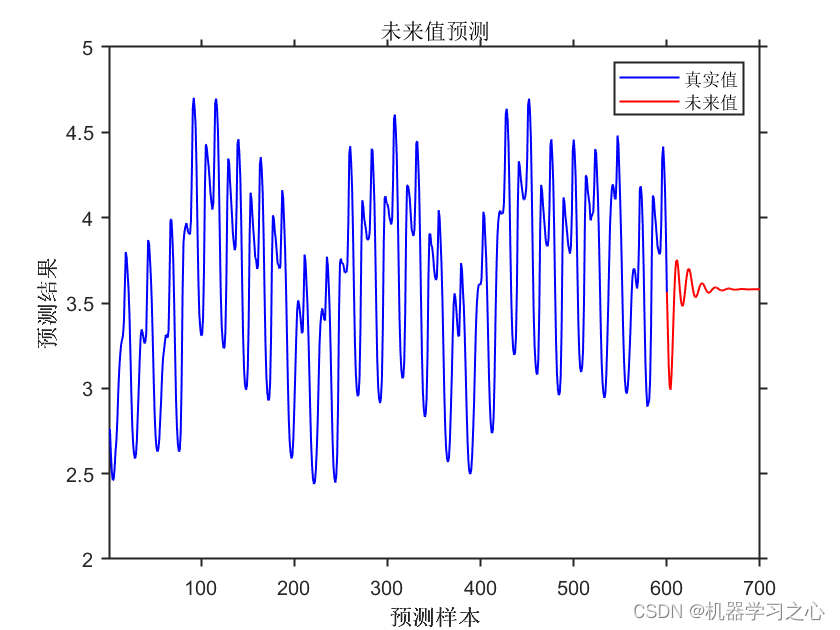
时序预测 | MATLAB实现基于CNN-GRU卷积门控循环单元的时间序列预测-递归预测未来(多指标评价)
时序预测 | MATLAB实现基于CNN-GRU卷积门控循环单元的时间序列预测-递归预测未来(多指标评价) 目录 时序预测 | MATLAB实现基于CNN-GRU卷积门控循环单元的时间序列预测-递归预测未来(多指标评价)预测结果基本介绍程序设计参考资料 预测结果 基本介绍 MATLAB实现基于CNN-GRU卷积…...

【李群李代数】李群控制器(lie-group-controllers)介绍——控制 SO(3) 空间中的系统的比例控制器Demo...
李群控制器SO(3)测试 测试代码是一个用于控制 SO(3) 空间中的系统的比例控制器。它通过计算控制策略来使当前状态逼近期望状态。该控制器使用比例增益 kp 进行参数化,然后进行一系列迭代以更新系统状态,最终检查状态误差是否小于给定的阈值。这个控制器用…...
PCI Express 总线)
DP读书:鲲鹏处理器 架构与编程(六)PCI Express 总线
处理器与服务器:PCI Express 总线 PCI Express 总线1. PCI Express 总线的特点a. 高速差分传输b. 串行传输c. 全双工端到端连接d. 基于多通道的数据传输方式e. 基于数据包的传输 2. PCI Express 总线的组成与拓扑结构a. 根复合体b. PCI Express桥c. 功能单元 3. PCI…...
Pyqt5-开源工具分解功能(文本拖拽)
开源第四篇:功能实现之拖拽功能与配置文件。 写这个功能的初衷,是因为,每次调试我都要手动敲命令,太麻烦了,想偷个懒,所以直接给这功能加上了,顺便衍生出了另一个想法,配置文件自动填写相关数据。 先看个简单的拖拽功能: 很明显吧,还是比较便捷的。所以我们本章,就在…...
Java版B/S架构 智慧工地源码,PC、移动、数据可视化智慧大屏端源码
智慧工地是什么?智慧工地主要围绕绿色施工、安全管控、劳务管理、智能管理、集成总控等方面,帮助工地解决运营、管理方面各个难点痛点。在互联网的加持下促进项目现场管理的创新与发展,实现工程管理人员与工程施工现场的整合,构建…...

无涯教程-PHP - Session选项
从PHP7 起, session_start()()函数接受一系列选项,以覆盖在 php.ini 中设置的会话配置指令。这些选项支持 session.lazy_write ,默认情况下此函数为on,如果会话数据已更改,则会导致PHP覆盖任何会话文件。 添加的另一个…...

The Age of Data and AI: Challenges and Opportunities
Simply put Abstract: This paper examines the impact of the “Age of Data” on the field of artificial intelligence (AI). With the proliferation of digital technologies and advancements in data collection, storage, and processing, organizations now have ac…...
WPF 项目中 MVVM模式 的简单例子说明
一、概述 MVVM 是 Model view viewModel 的简写。MVVM模式有助于将应用程序的业务和表示逻辑与用户界面清晰分离。 几个概念的说明: model :数据,界面中需要的数据,最好不要加逻辑代码view : 视图就是用户看到的UI结构 xaml 文件viewModel …...
基于nginx禁用访问ip
一、背景 网络安全防护时,禁用部分访问ip,基于nginx可快速简单实现禁用。 二、操作 1、创建 conf.d文件夹 在nginx conf 目录下创建conf.d文件夹 Nginx 扩展配置文件一般在conf.d mkdir conf.d 2、新建blocksip.conf文件 在conf.d目录新建禁用ip的扩展配置文…...

【第三阶段】kotlin语言的内置函数let
1.使用普通方法对集合的第一个元素相加 fun main() {//使用普通方法对集合的第一个元素相加var list listOf(1,2,3,4,5)var value1list.first()var resultvalue1value1println(result) }执行结果 2.使用let内置函数对集合的第一个元素相加 package Stage3fun main() {//使用…...

【C++入门到精通】C++入门 —— 模版(template)
阅读导航 前言一、模版的概念二、函数模版1. 函数模板概念2. 函数模板定义格式3. 函数模板的原理4. 函数模版的实例化🚩隐式实例化🚩显式实例化 5. 函数模板的匹配原则 三、类模板1. 类模板的定义格式2. 类模板的实例化 四、非类型模板参数1. 概念2. 定义…...

ARM汇编【3】:LOAD/STORE MULTIPLE PUSH AND POP
LOAD/STORE MULTIPLE 有时一次加载(或存储)多个值更有效。为此,我们使用LDM(加载多个)和STM(存储多个)。这些指令有一些变化,基本上只在访问初始地址的方式上有所不同。这是…...
Python之Qt输出UI
安装PySide2 输入pip install PySide2安装Qt for Python,如果安装过慢需要翻墙,则可以使用国内清华镜像下载,输入命令pip install --user -i https://pypi.tuna.tsinghua.edu.cn/simple PySide2,如下图, 示例Demo i…...

【1day】复现泛微OA某版本SQL注入漏洞
目录 一、漏洞描述 二、影响版本 三、资产测绘 四、漏洞复现 一、漏洞描述 泛微e-cology是一款由泛微网络科技开发的协同管理平台,支持人力资源、财务、行政等多功能管理和移动办公。泛微OA存在SQL注入漏洞,攻击者利用Web应用程序对用户输入验证上的疏忽,在输入的数据…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...
