你是真的“C”——C语言详解求两个正数最小公倍数的3种境界
C语言详解求两个正数最小公倍数的3种境界~😎
- 前言🙌
- 必备小知识~😘
- 求最小公倍数境界1~ 😊
- 求最小公倍数境界2~ 😊
- 求最小公倍数境界3~ 😊
- 总结撒花💞

博客昵称:博客小梦😊
最喜欢的座右铭:全神贯注的上吧!!!
作者简介:一名热爱C/C++,算法等技术、喜爱运动、热爱K歌、敢于追梦的小博主!
博主小留言:哈喽!😄各位CSDN的uu们,我是你的博客好友小梦,希望我的文章可以给您带来一定的帮助,话不多说,文章推上!欢迎大家在评论区唠嗑指正,觉得好的话别忘了一键三连哦!😘
前言🙌
哈喽各位友友们😊,我今天又学到了很多有趣的知识,现在迫不及待的想和大家分享一下!😘我仅已此文,手把手用C语言详解求两个正数最小公倍数的3种境界!这里举个求正数23 和正数 1782的最小公倍数为例。都是精华内容,可不要错过哟!!!😍😍😍
必备小知识~😘
什么是最小公倍数和最大公约数(最大公因数)?
- 最小公倍数就是可以整除这两个数的最小的数,例如:6和9的最小公倍数就是18,3和5的最小公倍数是15。==也可以说是两个数相乘除以他们的最大公约数==。
- 最大公约数的概念和最小公倍数正好相反,就是两个数都可以整除的最大的数,如3和5的最大公约数就是1,而6和9的最大公约数就是3。
求最小公倍数境界1~ 😊
境界1的算法求解过程分析:
- 这里的变量count 主要是求其循环比较的次数,通过这个可以比较看出三种境界算法的优劣性。
- 先定义一个count变量存储这两个数的最大值。
- 如果满足 max % a != 0 || max % b != 0,就让最大值加1,直到有一个能够被a和b同时整除的数就退出循环,这个数就是a和b的最小公倍数。
境界1源码: 😍
#include <stdio.h>
int main()
{int a = 0;int b = 0;scanf("%d %d", &a, &b);int count = 0;int max = a > b ? a : b;//先找到最大值while (max % a != 0 || max % b != 0){max++;count++;}printf("最小公倍数 = %d,比较运行的次数 = %d ", max,count);return 0;
}
代码结果运行图: 😍
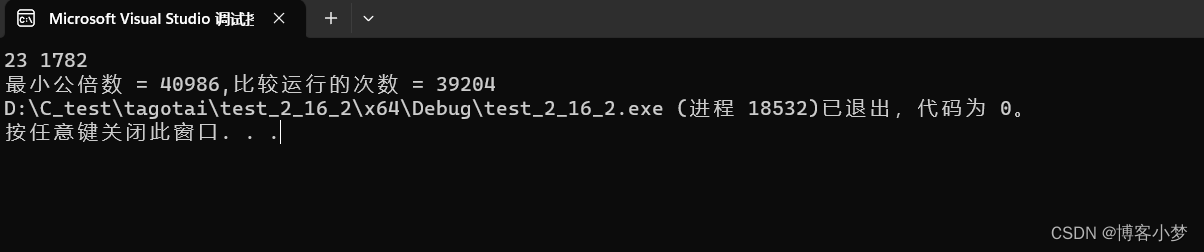 可见count = 39204 ,这个循环比较次数为39204,可见其算法效率非常低效。有没有更好的算法呢?请耐心看下文分析~
可见count = 39204 ,这个循环比较次数为39204,可见其算法效率非常低效。有没有更好的算法呢?请耐心看下文分析~
求最小公倍数境界2~ 😊
境界2的算法求解过程分析:
- 这里的变量count 主要是求其循环比较的次数,通过这个可以比较看出三种境界算法的优劣性。
- 定义一个变量i,让它从1开始,符合条件就自增。一个数的i倍,即乘以i其表达式结果就是这个数倍数,如果可以被另一个数整除,说明这个倍数就是这两个数的公倍数。因为i是从1开始自增的,所以第一个满足这个条件的一定是这两个数的最小公倍数啦。
境界2源码: 😍
#include <stdio.h>
int main()
{int a = 0;int b = 0;scanf("%d %d", &a, &b);int i = 1;int count = 0;while (i*a % b != 0){i++;count++;}printf("最小公倍数 = %d,比较运行的次数 = %d ",i*a,count);return 0;
}
代码结果运行图: 😍
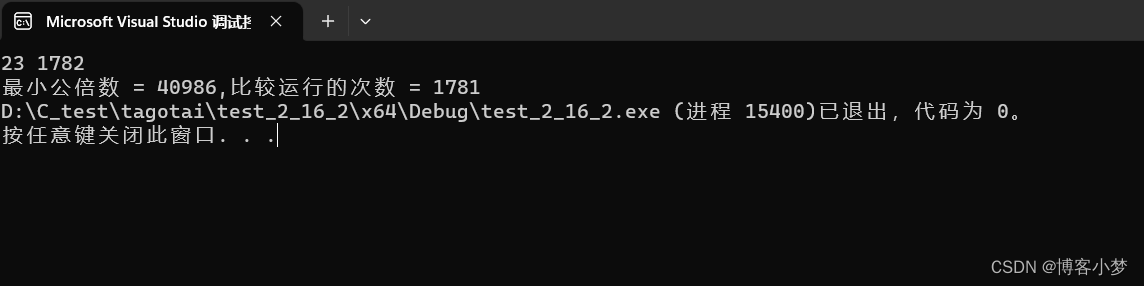
可见count = 1781 ,这个循环比较次数为1781,可见其算法效率比境界一有了明显的改善!那还有没有比这个更好的算法呢?请耐心看下文分析~
求最小公倍数境界3~ 😊
辗转相除法流程图解:
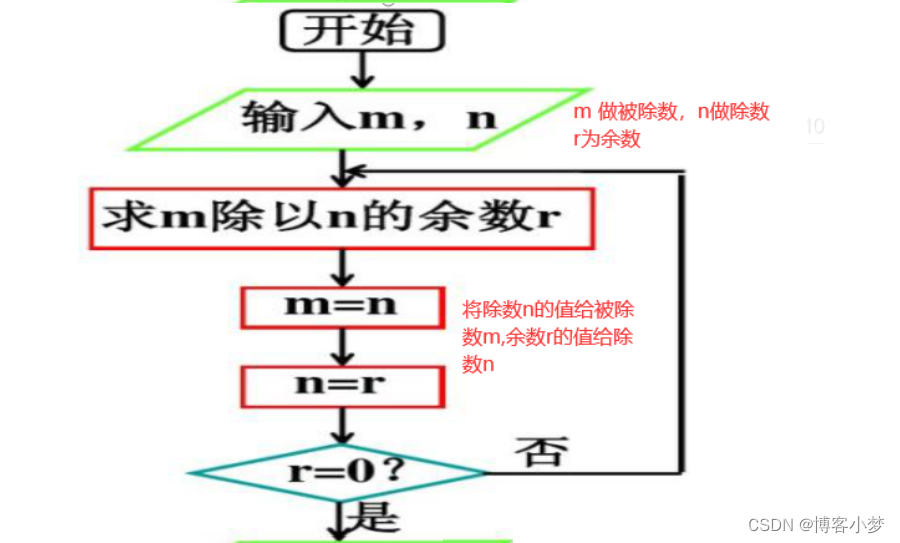
境界3源码: 😍
#include <stdio.h>
int main()
{int m = 0;int n = 0;scanf("%d %d", &m, &n);int a = m * n;int r = 0;int count = 0;while (r = m % n){m = n;n = r;count++;}printf("最小公倍数 = %d,比较运行的次数 = %d ", a / n, count);return 0;
}
代码结果运行图: 😍
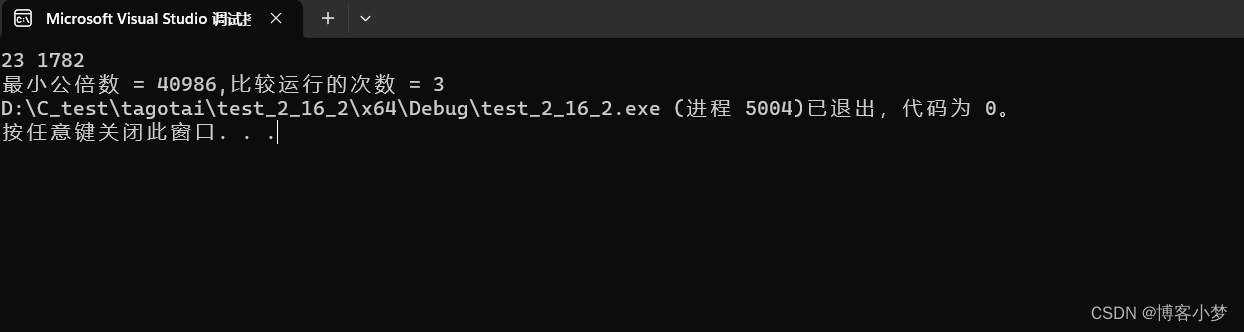
可见count = 3 ,这个循环比较次数为3,可见其算法效率真的是太惊人了!,但是这个算法还是有一个缺点,就是变量 a = m * n。如果这两个数很大,可能它们相乘的结果太大超出类型的最大数值。
总结撒花💞
本篇文章旨在带领大家利用C语言详解 - 求两个正数最小公倍数的3种境界。希望大家通过阅读此文有所收获!😘如果我写的有什么不好之处,请在文章下方给出你宝贵的意见😊。如果觉得我写的好的话请点个赞赞和关注哦~😘
相关文章:

你是真的“C”——C语言详解求两个正数最小公倍数的3种境界
C语言详解求两个正数最小公倍数的3种境界~😎前言🙌必备小知识~😘求最小公倍数境界1~ 😊求最小公倍数境界2~ 😊求最小公倍数境界3~ 😊总结撒花💞博客昵称:博客小梦😊 最喜…...

【java】Spring Cloud --Feign Client超时时间配置以及单独给某接口设置超时时间方法
文章目录feign配置(最常用)ribbon配置hystrix配置单独给某接口设置超时时间FeignClient面对服务级有三种超时时间配置feign配置(最常用) feign:sentinel:enabled: trueclient:config:default://全部服务配置connectTimeout: 5000…...

spark代码
RDD Tom,DataBase,80 Tom,Algorithm,50 Tom,DataStructure,60 Jim,DataBase,90 Jim,Algorithm,60 Jim,DataStructure,80 该系总共有多少学生; val lines sc.textFile("file:///usr/local/spark/sparksqldata/Data01.txt") val par lines.map(ro…...
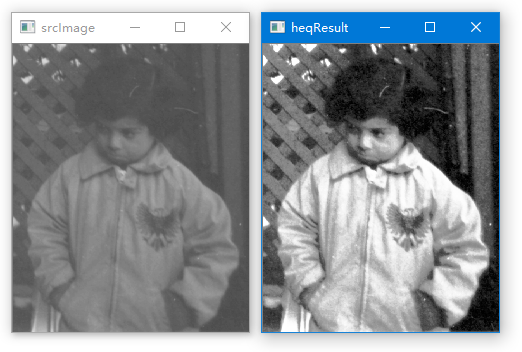
利用OpenCV的函数equalizeHist()对图像作直方图均衡化处理
如果一幅图像的灰度值集中在某个比较窄的区域,则图像的对比度会显得比较小,不便于对图像的分析和处理。 图像的直方图均衡化可以实现将原图像的灰度值范围扩大,这样图像的对比度就得到了提高,从而方便对图像进行后续的分析和处理…...

星河智联Android开发
背景:朋友内推,过了一周约面。本人 2019年毕业 20230208一面 1.自我介绍 2.为啥换工作 3.项目经历(中控面板、智能音箱、语音问的比较细) 4.问题 Handler机制原理?了解同步和异步消息吗?View事件分发…...

【C++】关联式容器——map和set的使用
文章目录一、关联式容器二、键值对三、树形结构的关联式容器1.set2.multiset3.map4.multimap四、题目练习一、关联式容器 序列式容器📕:已经接触过STL中的部分容器,比如:vector、list、deque、forward_list(C11)等,这些容器统称为…...

Promise的实现原理
作用:异步问题同步化解决方案,解决回调地狱、链式操作原理: 状态:pending、fufilled reject构造函数传入一个函数,resolve进入then,reject进入catch静态方法:resolve reject all any react ne…...
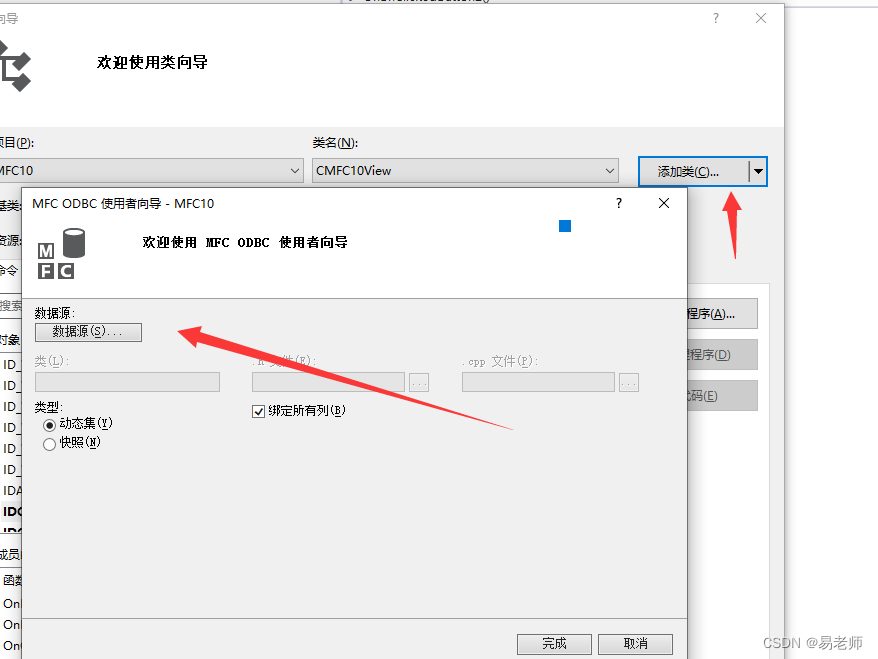
【MFC】数据库操作——ODBC(20)
ODBC:开放式数据库连接,是为解决异构数据库(不同数据库采用的数据存储方法不同)共享而产生的。ODBC API相对来说非常复杂,这里介绍MFC的ODBC类。 添加ODBC用户DSN 首先,在计算机中添加用户DSN:(WIN10下&a…...
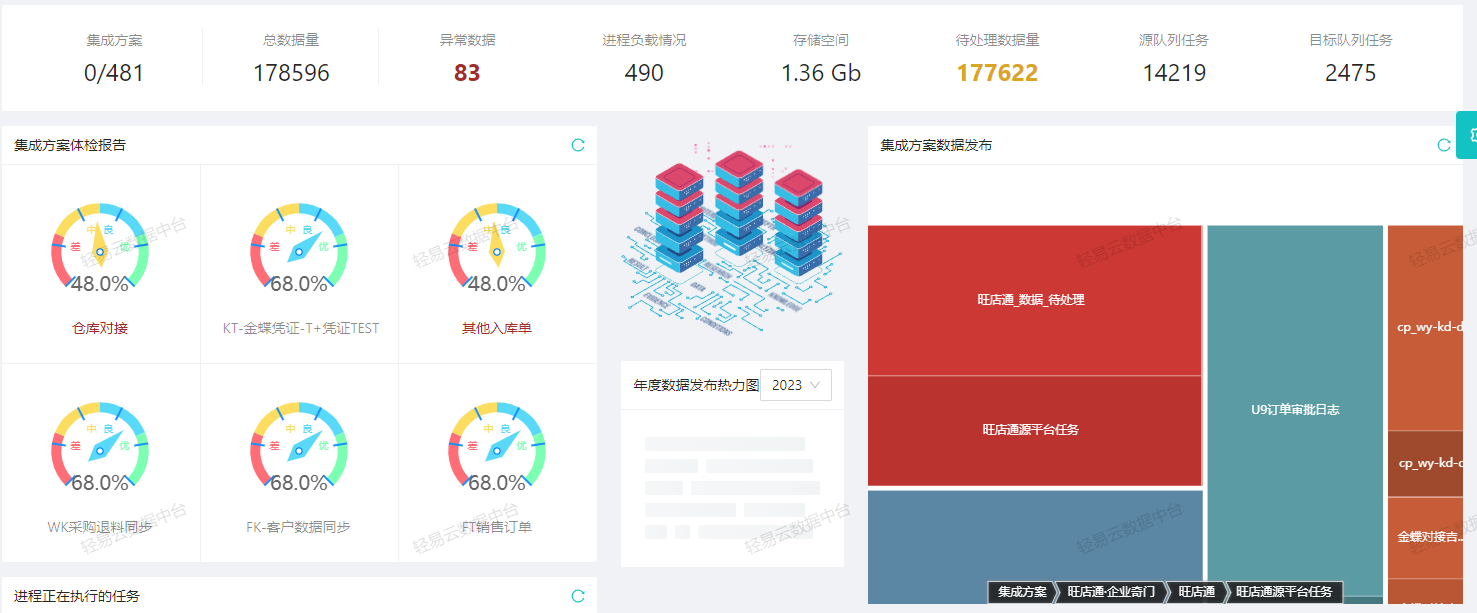
旺店通与金蝶云星空对接集成采购入库单接口
旺店通旗舰奇门与金蝶云星空对接集成采购入库单查询连通销售退货新增V1(12-采购入库单集成方案-P)数据源系统:旺店通旗舰奇门旺店通是北京掌上先机网络科技有限公司旗下品牌,国内的零售云服务提供商,基于云计算SaaS服务模式,以体系化解决方案…...
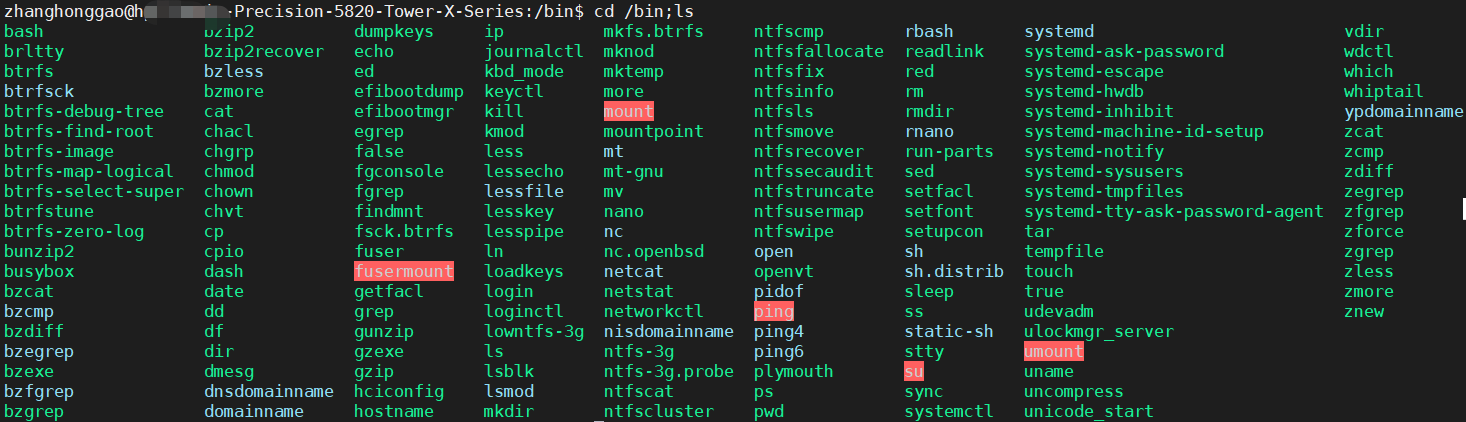
Linux基础-学会使用命令帮助
概述使用 whatis使用 man查看命令程序路径 which总结参考资料概述Linux 命令及其参数繁多,大多数人都是无法记住全部功能和具体参数意思的。在 linux 终端,面对命令不知道怎么用,或不记得命令的拼写及参数时,我们需要求助于系统的…...
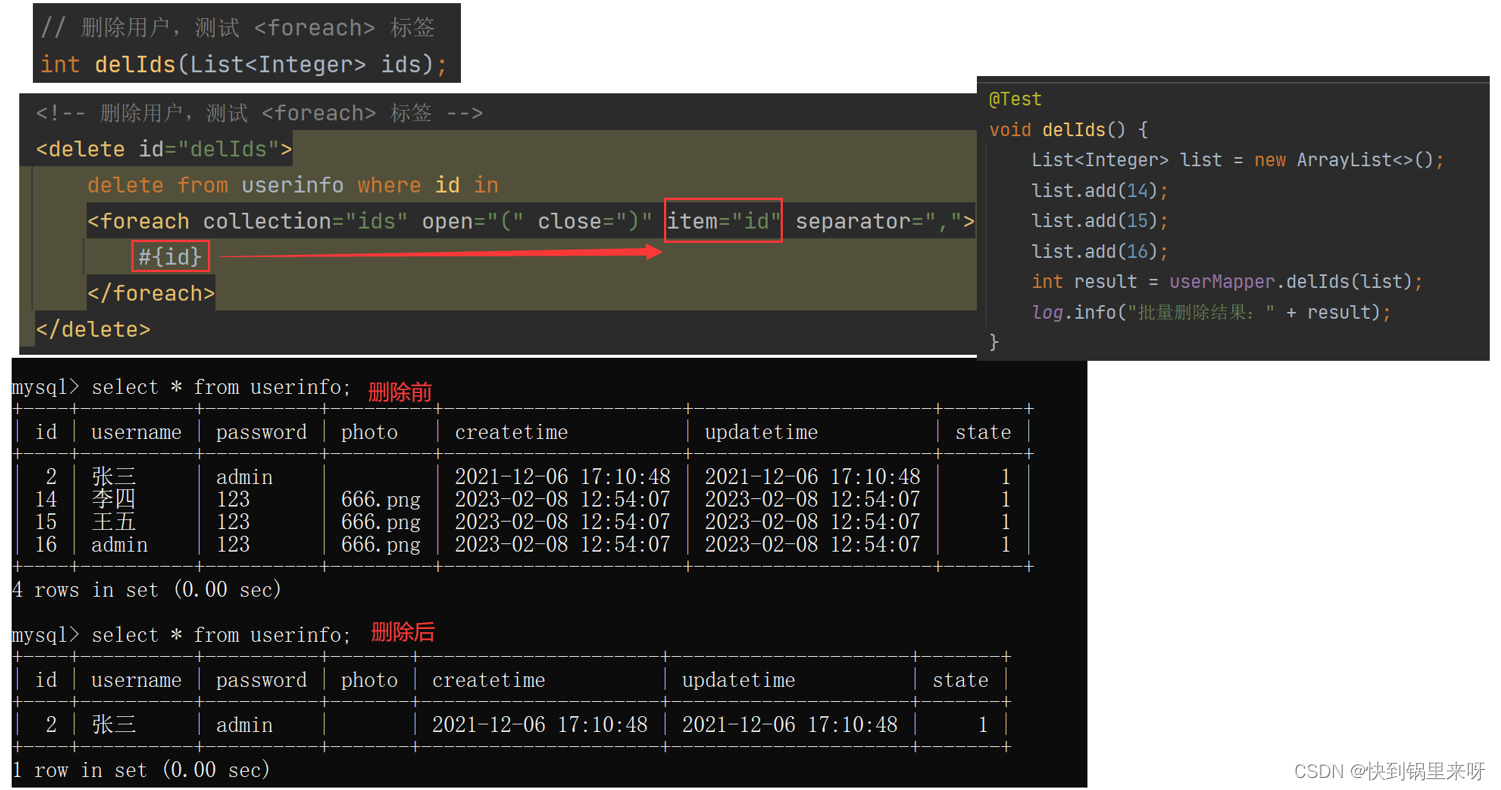
MyBatis 之四(动态SQL之 if、trim、where、set、foreach 标签)
文章目录动态 SQL1. if 标签2. trim 标签3. where 标签4. set 标签5. foreach 标签回顾一下,在上一篇 MyBatis 之三(查询操作 占位符#{} 与 ${}、like查询、resultMap、association、collection)中,学习了针对查询操作的相关知识点…...
 Practice 1006 Sign In and Sign Out)
PAT (Advanced Level) Practice 1006 Sign In and Sign Out
1006 Sign In and Sign Out题目翻译代码分数 25作者 CHEN, Yue单位 浙江大学At the beginning of every day, the first person who signs in the computer room will unlock the door, and the last one who signs out will lock the door. Given the records of signing in’…...

Android入门第64天-MVVM下瀑布流界面的完美实现-使用RecyclerView
前言 网上充满着不完善的基于RecyclerView的瀑布流实现,要么根本是错的、要么就是只知其一不知其二、要么就是一充诉了一堆无用代码、要么用的是古老的MVC设计模式。 一个真正的、用户体验类似于淘宝、抖音的瀑布流怎么实现目前基本为无解。因为本人正好自己空闲时也…...
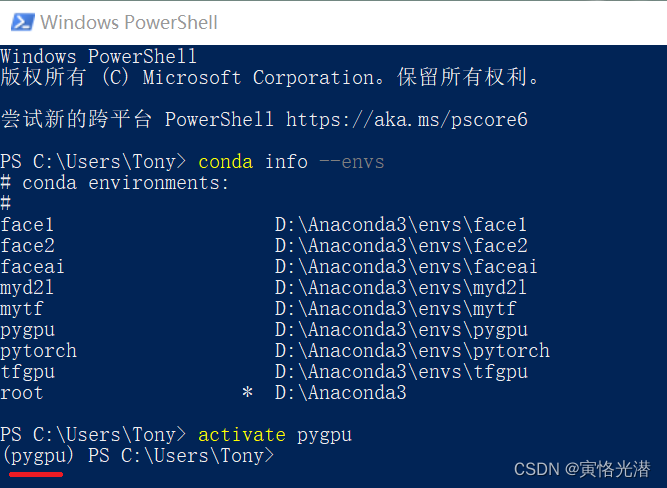
Windows PowerShell中成功进入conda虚拟环境
本人操作系统是Windows10(输入命令cmd或在运运行中输入winver查看)在cmd命令行中大家都很熟悉,很方便进入到指定创建了的虚拟环境中,那么在PowerShell中怎么进入呢?比如在VSCode中的TERMINAL使用的是PowerShell&#x…...

【C++】类与对象理解和学习(中)
专栏放在【C知识总结】,会持续更新,期待支持🌹六大默认成员函数前言每个类中都含有六大默认成员函数,也就是说,即使这个类是个空类,里面什么都没有写,但是编译器依然会自动生成六个默认成员函数…...
大英复习单词和翻译)
每日英语学习(11)大英复习单词和翻译
2023.2.20 单词 1.contemplate 思考、沉思 2.spark 激起 3.venture 冒险 4.stunning 极好的 5.dictate 影响 6.diplomatic 外交的 7.vicious 恶性的 8.premier 首要的 9.endeavor 努力 10.bypass 绕过 11.handicaps 不利因素 12.vulnerable 脆弱的 13.temperament 气质、性格…...

x79主板M.2无法识别固态硬盘
问题描述: 这几天在装电脑,买了块M.2接口固态硬盘。装上去始终无法读取到硬盘,一开始以为是寨板Bios问题不支持M.2的设备。更新了最新的BIOS然后还是没有识别出来,然而将日常用的电脑PM510硬盘装上发现可以识别,而且日常用电脑也…...

配置Tomcat性能优化
配置Tomcat性能优化 📒博客主页: 微笑的段嘉许博客主页 💻微信公众号:微笑的段嘉许 🎉欢迎关注🔎点赞👍收藏⭐留言📝 📌本文由微笑的段嘉许原创! Ǵ…...
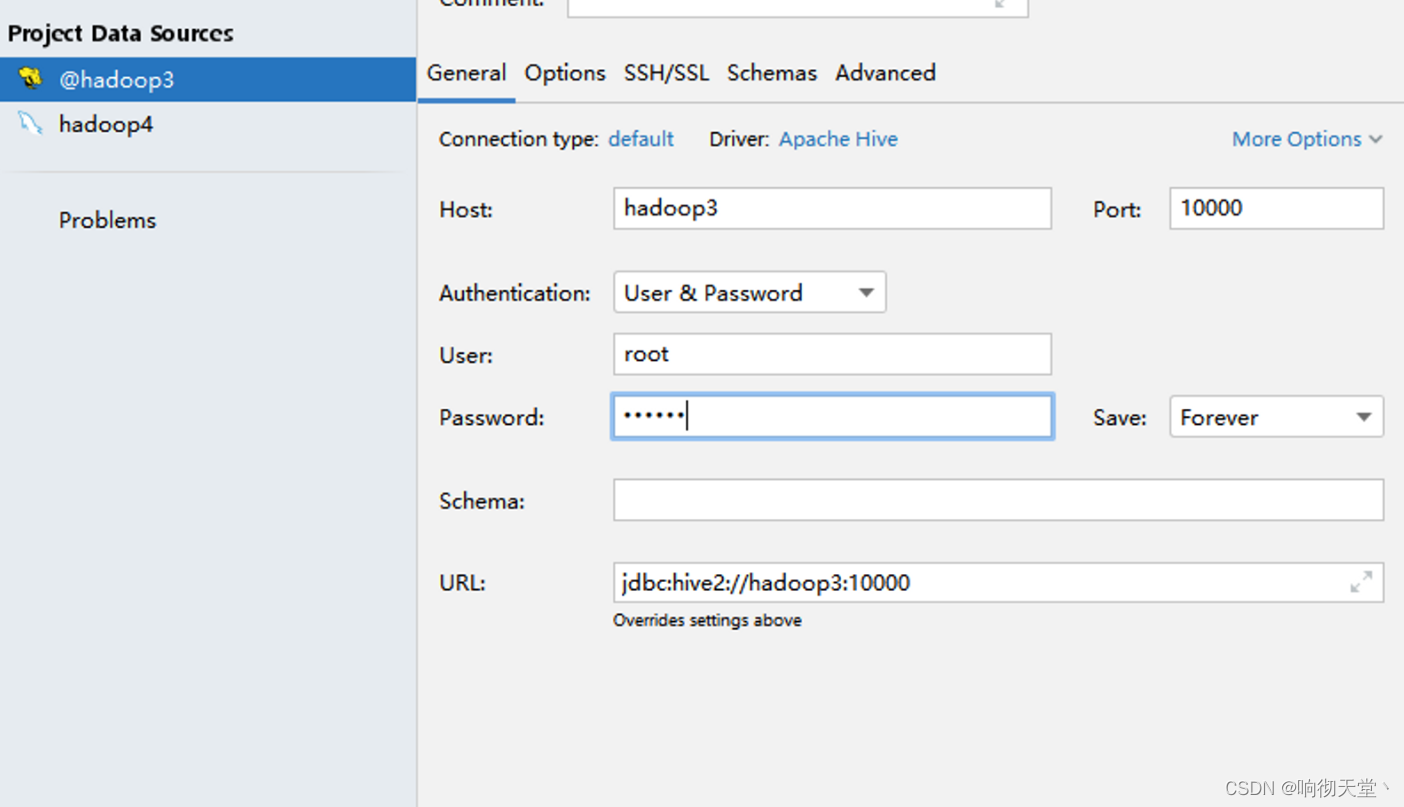
Hive3 安装方式详解,datagrid自定义驱动连接hive
1 Hive的安装方式 hive的安装一共有三种方式:内嵌模式、本地模式、远程模式。 元数据服务(metastore)作用是:客户端连接metastore服务,metastore再去连接MySQL数据库来存取元数据。有了metastore服务,就可以有多个客户端同时连接…...
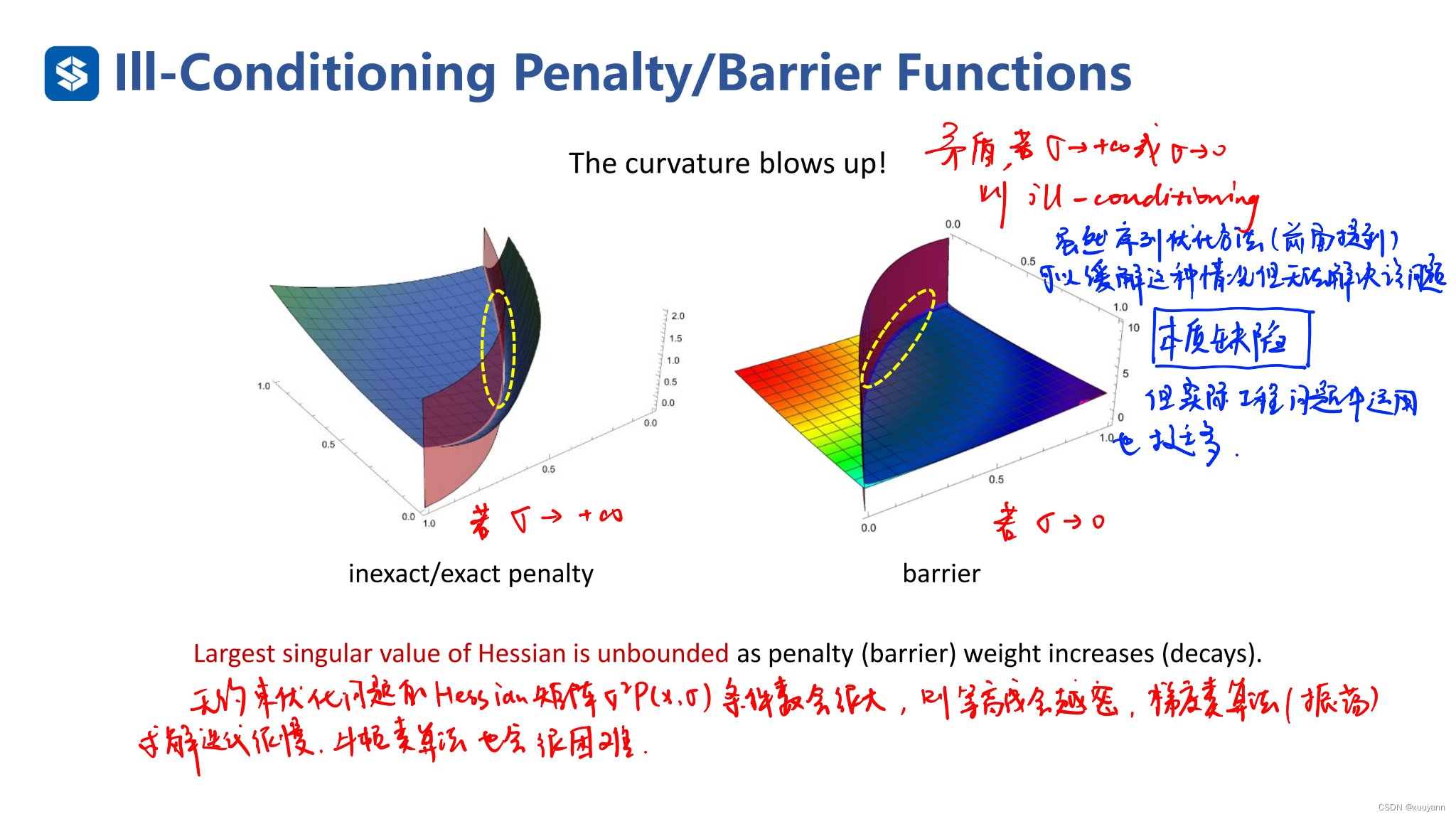
约束优化:约束优化的三种序列无约束优化方法(罚函数法)
文章目录约束优化:约束优化的三种序列无约束优化方法(罚函数法)外点罚函数法L2-罚函数法:非精确算法对于等式约束对于不等式约束L1-罚函数法:精确算法内点罚函数法:障碍函数法参考文献约束优化:…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

