【算法随记】在计算过程中模的情况
https://leetcode.cn/problems/power-of-heroes/

计算过程中,可以放心模的情况:
加减乘
先模再加再模和直接加再模一样
a m o d m + b m o d m ≡ a + b ( m o d m ) a\mod m+b\mod m ≡ a+b \ (\mod m) amodm+bmodm≡a+b (modm)
先模再减再模和直接减再模一样
a m o d m − b m o d m ≡ a − b ( m o d m ) a\mod m-b\mod m ≡ a-b \ (\mod m) amodm−bmodm≡a−b (modm)
先模再乘再模和直接乘再模一样
a m o d m × b m o d m ≡ a × b ( m o d m ) a\mod m \times b\mod m ≡ a \times b \ (\mod m) amodm×bmodm≡a×b (modm)
如果 a≡b(mod m) 且有 c≡d(mod m),那么下面的模运算律成立:
a+c≡b+d(mod m)
a−c≡b−d(mod m)
a×c≡b×d(mod m)
除法没有这个性质
相关文章:

【算法随记】在计算过程中模的情况
https://leetcode.cn/problems/power-of-heroes/ 计算过程中,可以放心模的情况: 加减乘 先模再加再模和直接加再模一样 a m o d m b m o d m ≡ a b ( m o d m ) a\mod mb\mod m ≡ ab \ (\mod m) amodmbmodm≡ab (modm) 先模再减再模和直接减再模…...
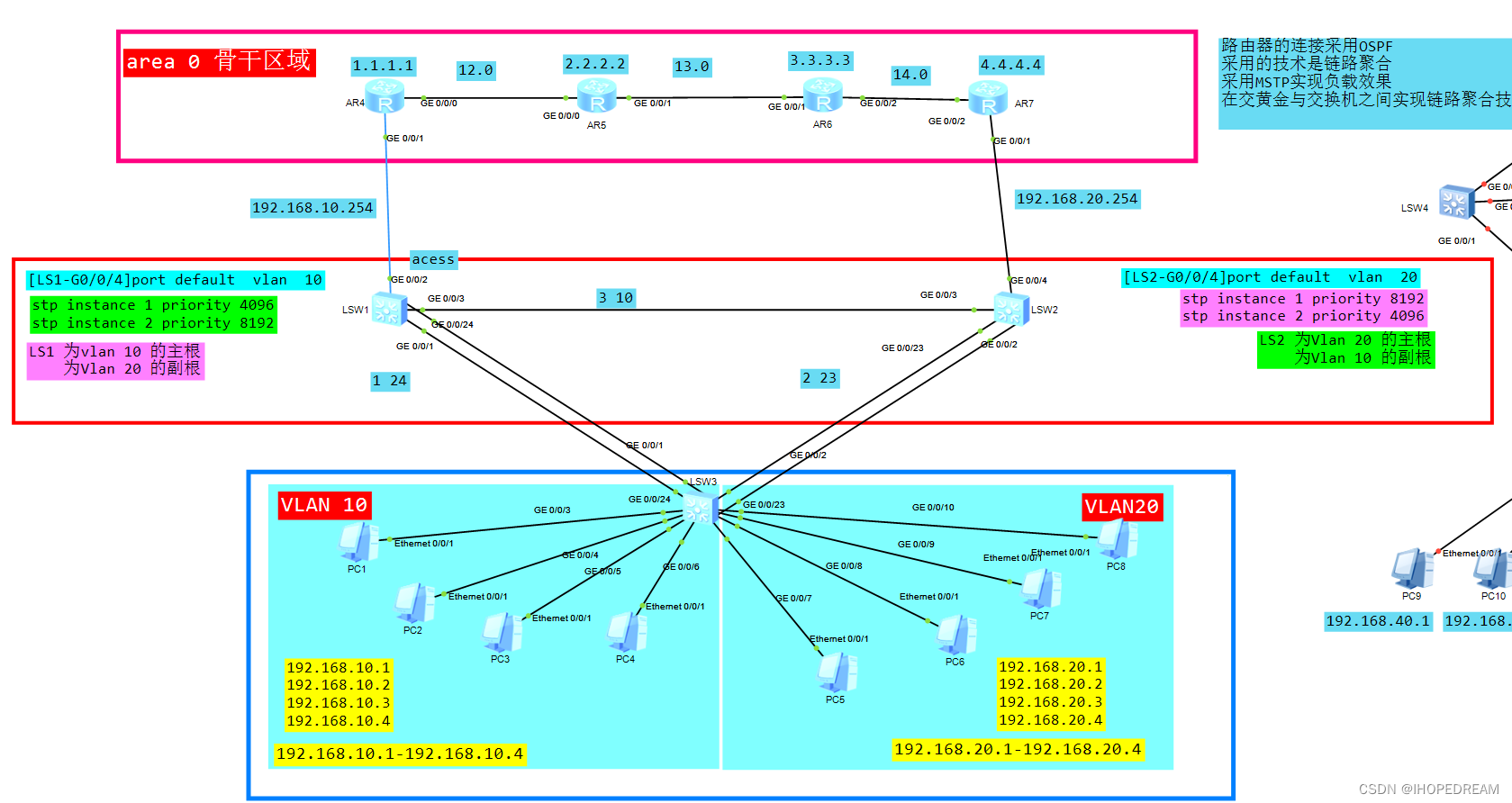
MSTP多生成树协议(第二课)
MSTP负载均衡 实验 需求 1)PC1属于 vlan 10 ,IP地址为 192.168.10.1/24, 网关为 192.168.10.2542)PC2属于 vlan 20 ,IP地址为 192.168.20.1/24, 网关为 192.168.20.254**3)确保PC1与PC2互通4…...

数组指针、函数指针、指针数组、函数 指针数组、指针函数详细总结
1.数组指针概念和应用 首先数组指针应该是一个数组,它的定义如下: 数组指针,指的是数组名的指针,即数组首元素地址的指针。即是指向数组的指针。例:int (*p)[10]; p即为指向数组的指针,又称数组指针。 数…...
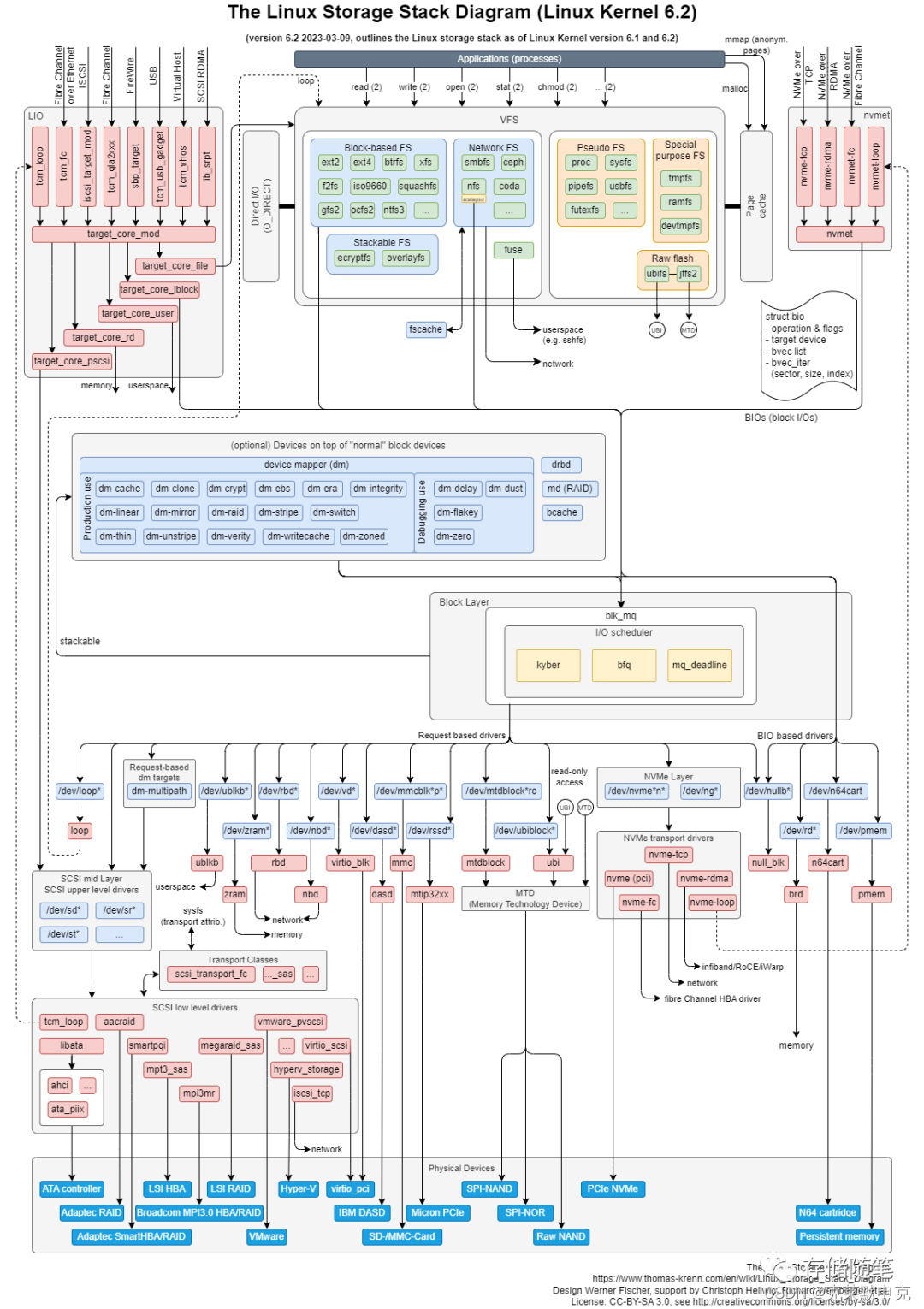
Linux存储学习笔记
相关文章 Linux 存储系列|请描述一下文件的 io 栈? - tcpisopen的文章 - 知乎 https://zhuanlan.zhihu.com/p/478443978 深入学习 Linux 操作系统的存储 IO 堆栈 - KaiwuDB的文章 - 知乎 https://zhuanlan.zhihu.com/p/636720297 linux存储栈概览 - st…...
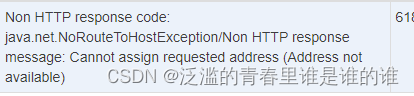
ubuntu执行jmeter端口不够用报错(Address not available)
ubuntu执行jmeter端口不够用报错(Address not available) 解决方案 // 增加本地端口范围 echo 1024 65000 > /proc/sys/net/ipv4/ip_local_port_range// 启用快速回收TIME_WAIT套接字 sudo sysctl -w net.ipv4.tcp_tw_recycle 1// 启用套接字的重用 sudo sysctl -w net.ipv4…...

MongoDB:简单的增删改查操作
一.概述 本篇文章介绍在Navicat中对MongoDB数据库进行增删改查操作,在后面会介绍在Spring Boot中使用MongoTemplate对MongoDB数据库进行相关操作.如有必要可以先看看前面几篇文章. MongoDB:MySQL,Redis,ES,MongoDB的应用场景 MongoDB:数据库初步应用 二.在Navicat进行增删改…...
)
网络编程(域套接字)
一、域套接字的概念 1.只能做一台主机内的进程间通信,协议族(地址族)指定为:AF_UNIX AF_LOCAL 2.bsp-lcd: s类型文件,就是域套接字 3.如果客户端不手动绑定,则操作系统不会创建一个套接字文件…...

探索短视频小程序/小年糕
短视频小程序的兴起,为创作者提供了一个全新的平台,让他们能够以更专业的方式展现自己的作品。这种创作形式不仅要求作品内容足够精彩还需要有深度的思考和逻辑性的呈现。本文将探索短视频小程序的专业与深度的创作之道,帮助创作者更好地发挥…...
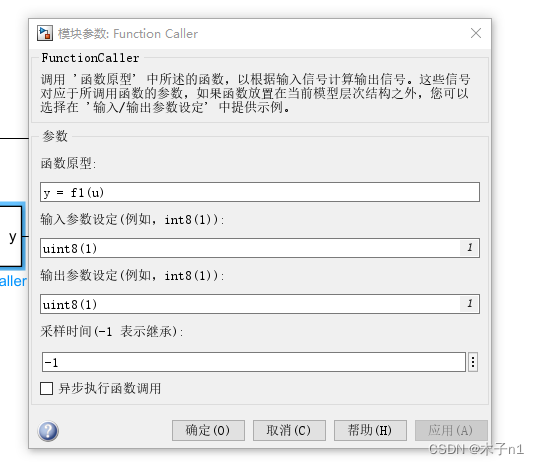
基于MATLAB开发AUTOSAR软件应用层Code mapping专题-part 7 Function callers标签页介绍
不知不觉这个code-mapping专题已经写了6篇文章了,今天是我们这个专题的最后一篇文章了介绍Function callers 这个其实很简单,以前的文章里也有提到CS接口实现两个SWC之间的CS调用,我们在从Code-mapping的角度在说下 首先还是看下模型 我们还记得在simulink里我们用function…...

ARM开发(cortex-A7核中断实验)
1.实验目的:实现KEY1/LEY2/KE3三个按键,中断触发打印一句话,并且灯的状态取反; key1 ----> LED3灯状态取反; key2 ----> LED2灯状态取反; key3 ----> LED1灯状态取反; 2.分析框图: …...
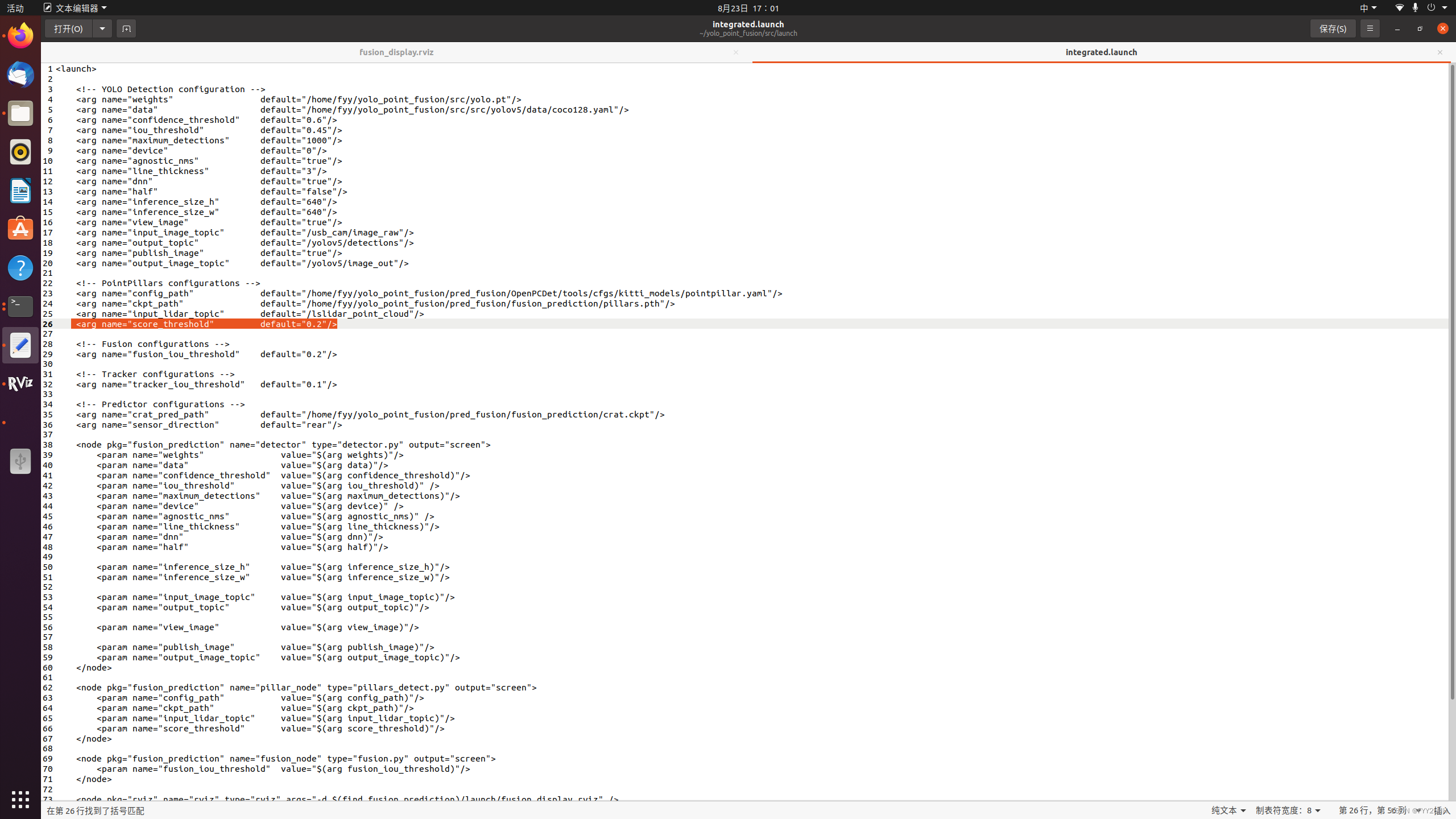
关于融合项目点云pointpillars检测不显示三维检测框问题的解决
这个问题主要还是launch文件中出现了一些偏差。 launch文件的第26行 这里原先是0.6,在检测kitti的时候是0.6,由于kitti是64线激光雷达,我个人用的是16线激光雷达,所以把0.6降到了0.2.出现了三维检测框,问题解决...
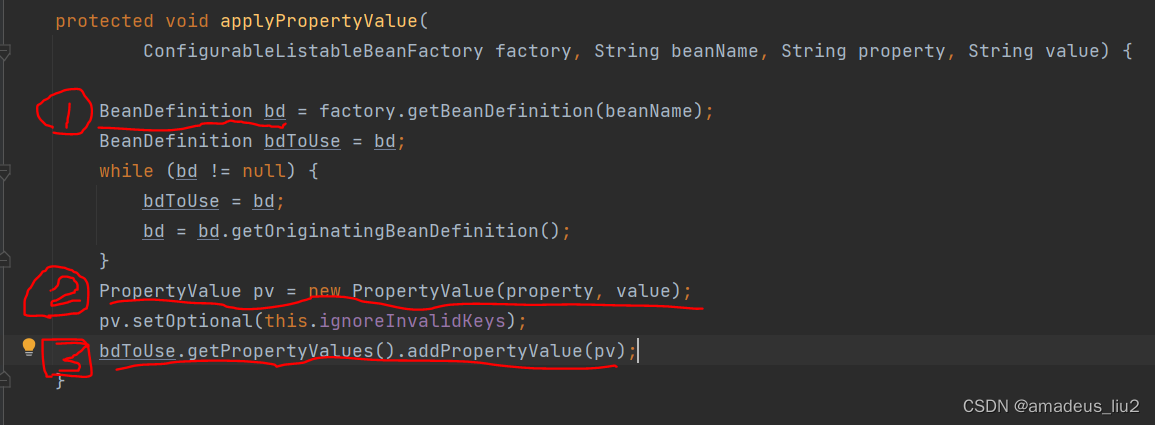
spring复习:(57)PropertyOverrideConfigurer用法及工作原理
一、属性配置文件 dataSource.urljdbc:mysql://xxx.xxx.xxx.xxx/test dataSource.usernameroot dataSource.passwordxxxxxx dataSource.driverClassNamecom.mysql.jdbc.Driver #dataSource.typecom.alibaba.druid.pool.DruidDataSource二、spring配置文件 <?xml version&…...

在axios中获取文件上传进度
1.在axios 全局配置的文件中加入一个postFile 方法在上传文件时调用。 export function postFile(url, params,config) {return new Promise((resolve, reject) > {axios.post(url, params,config).then(res > {resolve(res);}).catch(err > {reject(err);})}) } 2.…...

黑马头条-kafka配置
生产者配置 NAMEDESCRIPTIONTYPEDEFAULTVALID VALUESIMPORTANCEbootstrap.servershost/port列表,用于初始化建立和Kafka集群的连接。列表格式为host1:port1,host2:port2,…,无需添加所有的集群地址,kafka会根据提供的地址发现其他的地址&…...
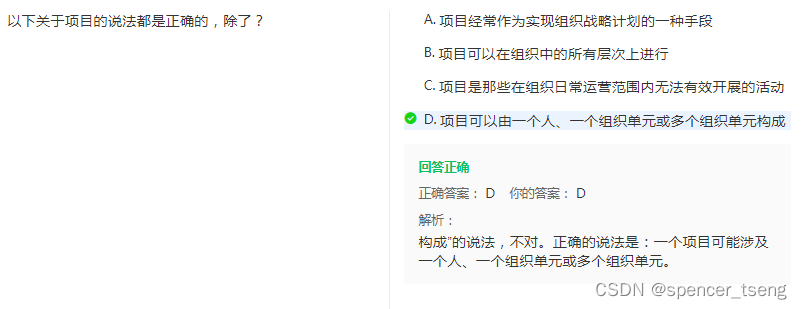
PMP P-01 Basic Knowledge
PMP基础知识...
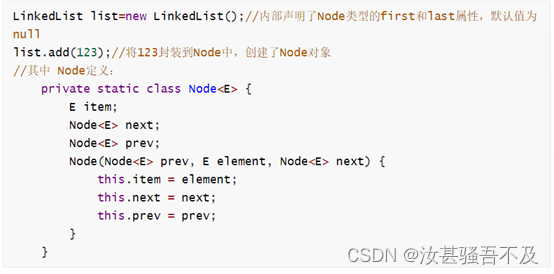
java八股文面试[数据结构]——ArrayList和LinkedList区别
ArrayList和LinkedList的异同 二者的线程都不安全,相对线程安全的Vector,执行效率高。此外,ArrayList时实现了基于动态数组的数据结构,LinkedList基于链表的数据结构,对于随机访问get和set,ArrayList觉得优于LinkedLis…...
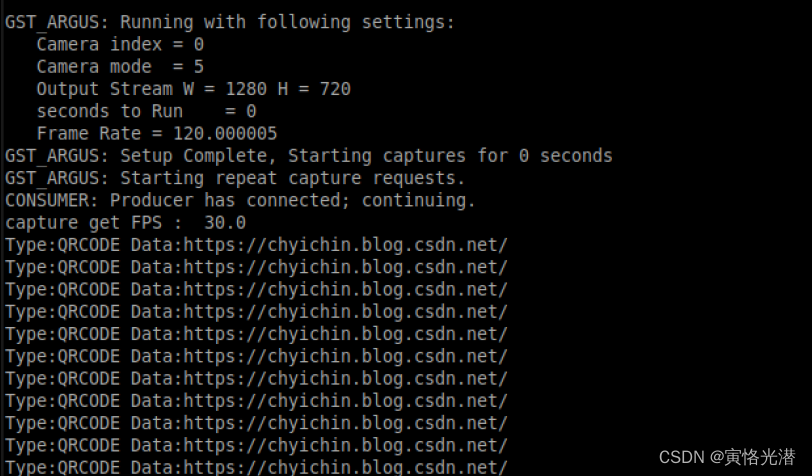
OpenCV中QR二维码的生成与识别(CIS摄像头解析)
1、QR概述 QR(Quick Response)属于二维条码的一种,意思是快速响应的意思。QR码不仅信息容量大、可靠性高、成本低,还可表示汉字及图像等多种文字信息、其保密防伪性强而且使用非常方便。更重要的是QR码这项技术是开源的,在移动支付、电影票、…...
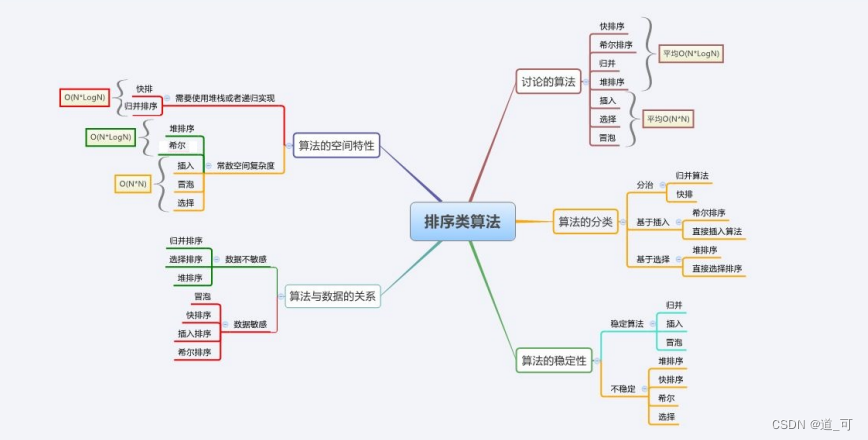
常见排序集锦-C语言实现数据结构
目录 排序的概念 常见排序集锦 1.直接插入排序 2.希尔排序 3.选择排序 4.堆排序 5.冒泡排序 6.快速排序 hoare 挖坑法 前后指针法 非递归 7.归并排序 非递归 排序实现接口 算法复杂度与稳定性分析 排序的概念 排序 :所谓排序,就是使一串记录&#…...

css 实现四角边框样式
效果如图 此图只实现 左下与右下边角样式 右上与左上同理 /* 容器 */ .card-mini {position: relative; } /* 左下*/ .card-mini::before {content: ;position: absolute;left: 0;bottom: 0;width: 20px;height: 20px;border-bottom: 2px solid #253d64;border-left: 2px so…...
机器学习深度学习——自注意力和位置编码(数学推导+代码实现)
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er 🌌上期文章:机器学习&&深度学习——注意力分数(详细数学推导代码实现) 📚订阅专栏:机器学习…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
