【期末复习】例题说明Prim算法与Kruskal算法
点睛
Prim与Kruskal算法是用来求图的最小生成树的算法。最小生成树有n个顶点,n-1条边,不能有回路。
Prim算法
Prim算法的特点是从个体到整体,随机选定一个顶点为起始点出发,然后找它的权值最小的边对应的另一个顶点,这两个顶点就构成了新的个体(连通图),然后在这两个顶点的所有边中找权值最小的边对应的另一个顶点(前提是加进来不能导致已有的顶点所在的连通图构成回路),就这样直到所有顶点都并入同一个连通图,算法结束。
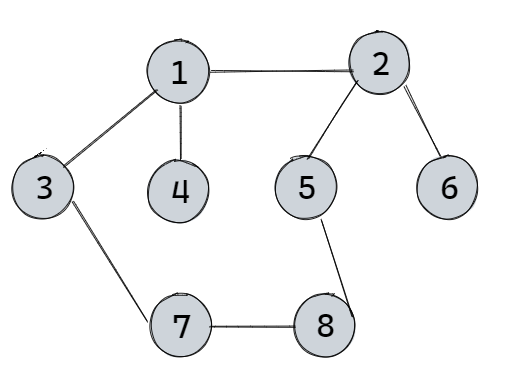
例1利用Prim算法求下图的一棵最小生成树,设顶点1为起始点,写出求解过程。

答案:
找到顶点1权值最小的边(1,3),则顶点1和3构成新的连通图
找到顶点1和3中权值最小的边(3,4),则顶点1,3,4构成新的连通图
找到顶点1,3,4中权值最小的边(4,7),则顶点1,3,4,7构成新的连通图
找到顶点1,3,4,7中权值最小的边(7,8),则顶点1,3,4,7,8构成新的连通图
找到顶点1,3,4,7,8中权值最小的边(8,6),则顶点1,3,4,7,8,6构成新的连通图
找到顶点1,3,4,7,8中权值最小的边(8,5),则顶点1,3,4,7,8,6,5构成新的连通图
找到顶点1,3,4,7,8,5中权值最小的边(1,2),则顶点1,3,4,7,8,6,5,2构成新的连通图
至此Prim算法结束,找到最小生成树如下图

Kruskal算法
Kruskal算法的特点是从整体到个体,它把整个图(默认是无向连通图)看做n个独立的顶点,然后把图的所有带权边根据权值大小升序排列存入一个序列中。最后依次从序列中取出这些边加入n个独立的顶点使它们成为同一个连通图的一部分,只要取出的边的数量不到n-1就一直取。在取的过程中如果有一条边的加入会造成回路,则跳过选下一个权值稍大的边。
例2利用Kruskal算法求下图的一棵最小生成树,写出求解过程。

答案:
将图中所有的边按照权值大小升序排列存入集合中,结果如下:
{(1,2), (1,3), (1,4), (2,5), (2,6), (3,4, (3,7), (4, 5), (4,7), (5,6), (5, 8), (6,8), (7,8)}
从集合中取出边(1,2),顶点1和2构成一个新的连通图
从集合中取出边(1,3),顶点1,2,3构成一个新的连通图
从集合中取出边(1,4),顶点1,2,3,4构成一个新的连通图
从集合中取出边(2,5),顶点1,2,3,4,5构成一个新的连通图
从集合中取出边(2,6),顶点1,2,3,4,5,6构成一个新的连通图
从集合中取出边(3,4),会在顶点1,3,4之间构成回路跳过
从集合中取出边(3,7),顶点1,2,3,4,5,6,7构成一个新的连通图
从集合中取出边(4,5),会在顶点1,2,4,5构成回路,跳过
从集合中取出边(4,7),顶点1,3,4,7构成回路,跳过
从集合中取出边(5,6),顶点2,5,6构成回路,跳过
从集合中取出边(5,8),顶点1,2,3,4,5,6,7,8构成一个新的连通图
边的个数达到n-1,结束,最小生成树如下图:
相关文章:

【期末复习】例题说明Prim算法与Kruskal算法
点睛Prim与Kruskal算法是用来求图的最小生成树的算法。最小生成树有n个顶点,n-1条边,不能有回路。Prim算法Prim算法的特点是从个体到整体,随机选定一个顶点为起始点出发,然后找它的权值最小的边对应的另一个顶点,这两个…...
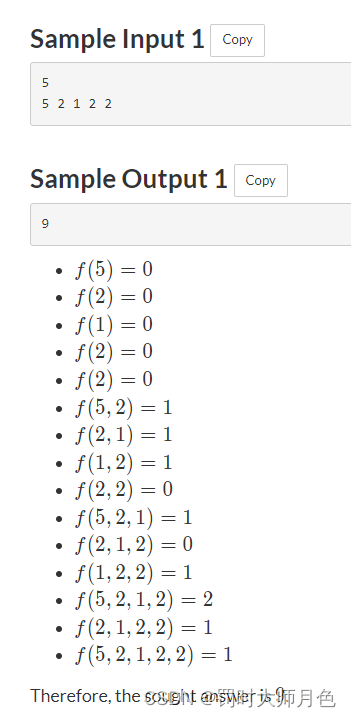
AtCoder Beginner Contest 290 A-E F只会n^2
ABC比较简单就不再复述 D - Marking 简要题意 :给你一个长度为nnn的数组,下标为0到n−10 到 n-10到n−1,最初指针位于0,重复执行n-1次操作,每次操作的定义为将当前指针加上ddd,如果该位置为空(未填数),否则我们向右找到第一个为空…...
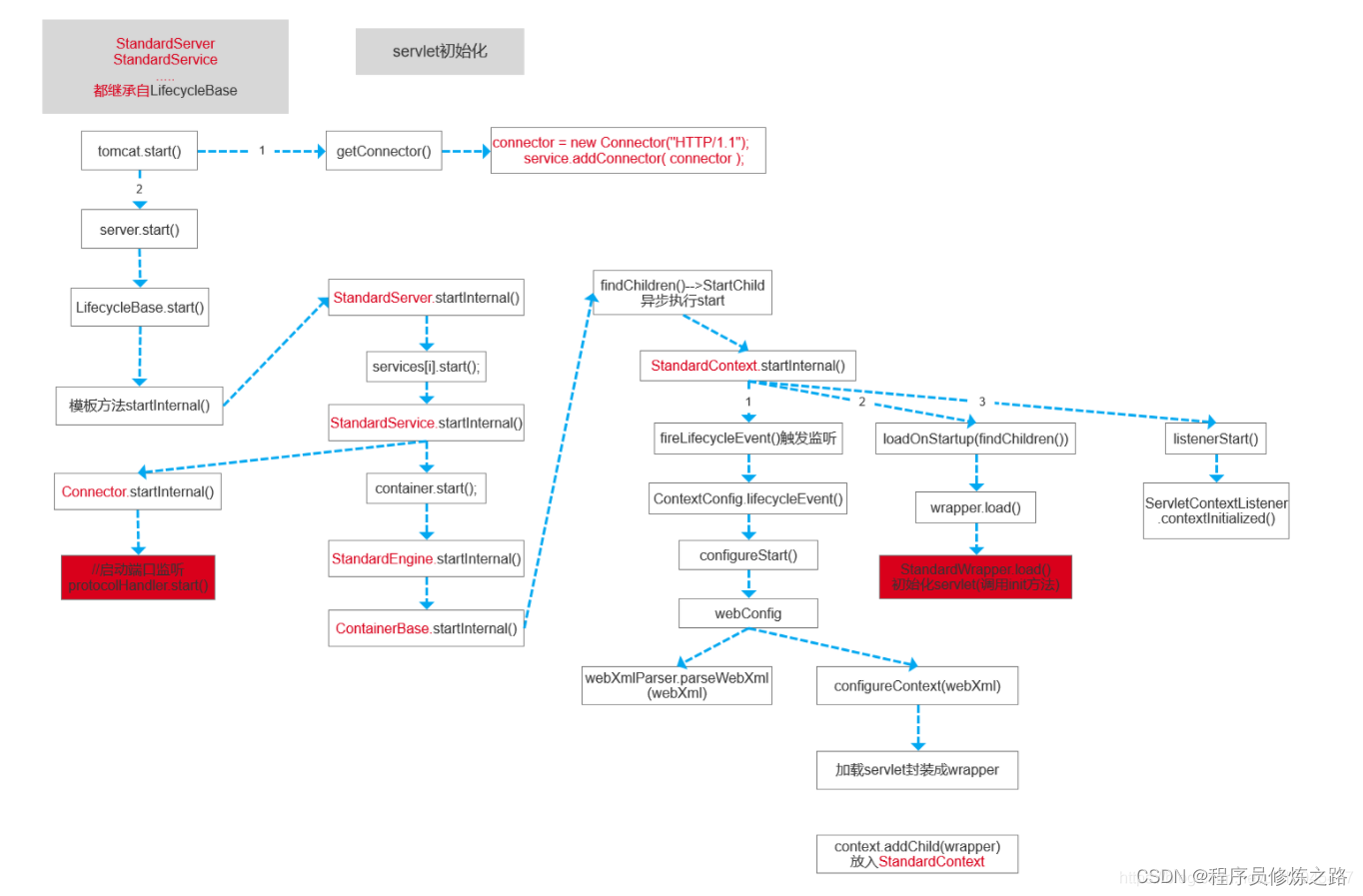
springMvc源码解析
入口:找到springboot的自动配置,将DispatcherServlet和DispatcherServletRegistrationBean注入spring容器(DispatcherServletRegistrationBean间接实现了ServletContextInitializer接口,最终ServletContextInitializer的onStartup…...
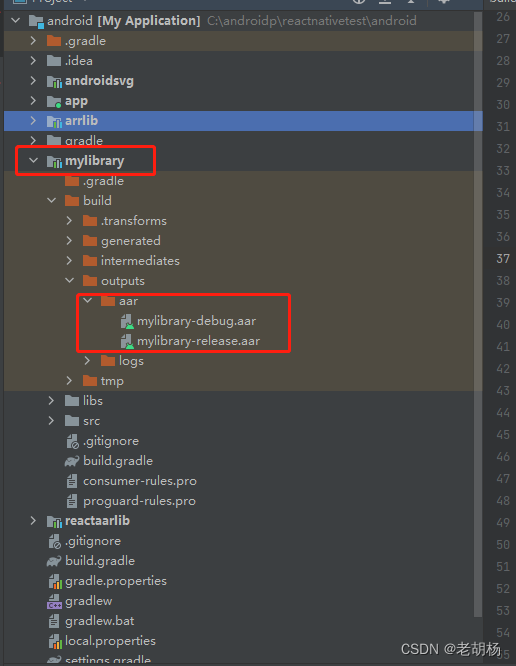
采用aar方式将react-native集成到已有安卓APP
关于react-native和android的开发环境搭建、环境变量配置等可以查看官方文档。 官方文档地址 文章中涉及的node、react等版本: node:v16.18.1 react:^18.1.0 react-native:^0.70.6 gradle:gradle-7.2开发工具:VSCode和android studio 关于react-native和…...
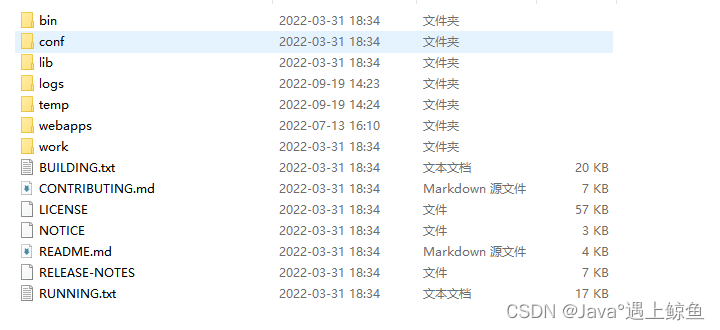
Tomcat目录介绍,结构目录有哪些?哪些常用?
bin 启动,关闭和其他脚本。这些 .sh文件(对于Unix系统)是这些.bat文件的功能副本(对于Windows系统)。由于Win32命令行缺少某些功能,因此此处包含一些其他文件。 比如说:windows下启动tomcat用的…...
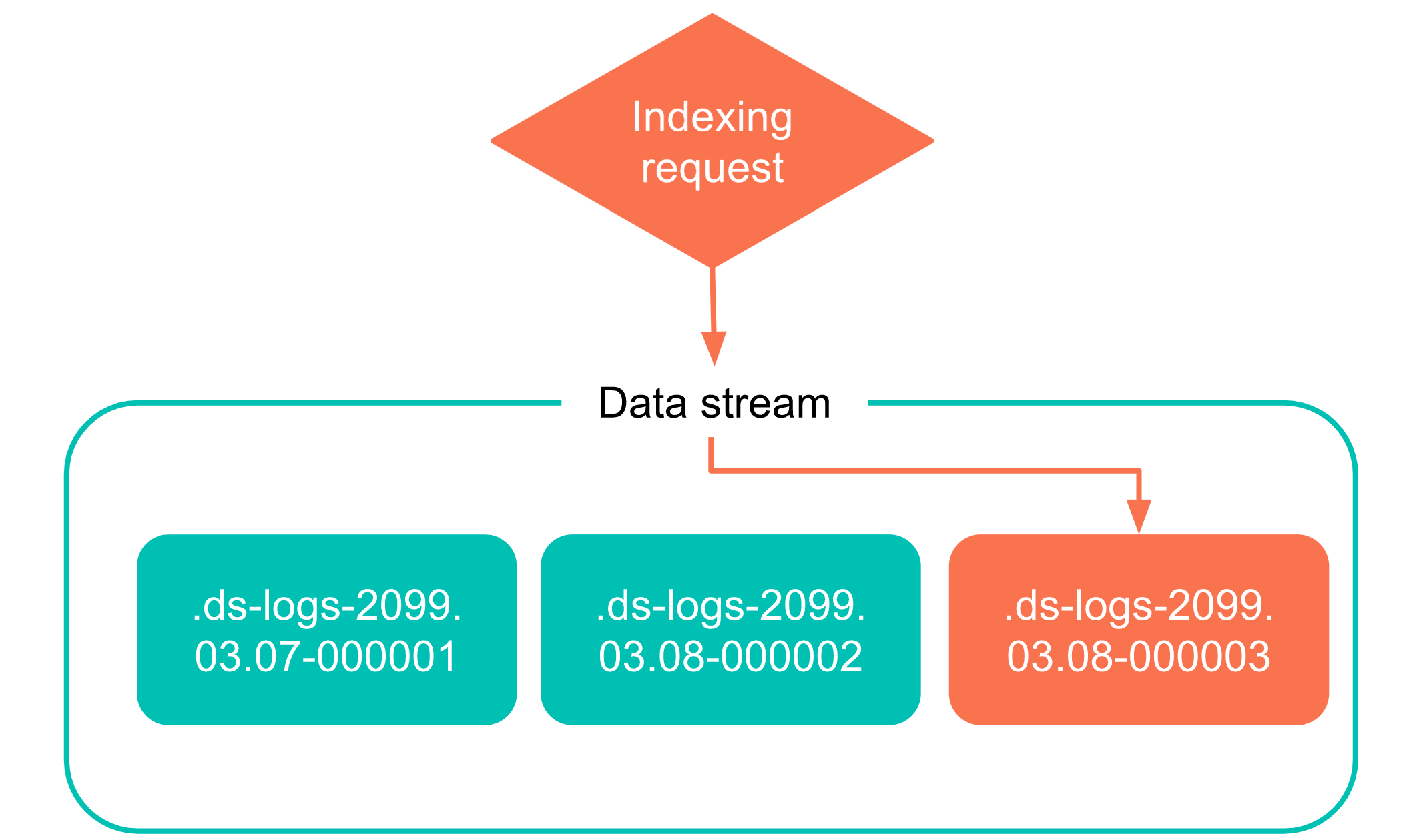
Elasticsearch也能“分库分表“,rollover实现自动分索引
一、自动创建新索引的方法 MySQL的分库分表大家是非常熟悉的,在Elasticserach中有存在类似的场景需求。为了不让单个索引太过于庞大,从而引发性能变差等问题,我们常常有根据索引大小、时间等创建新索引的需求,解决方案一般有两个…...

6 大经典机器学习数据集,3w+ 用户票选得出,建议收藏
内容一览:本期汇总了超神经下载排名众多的 6 个数据集,涵盖图像识别、机器翻译、遥感影像等领域。这些数据集质量高、数据量大,经历人气认证值得收藏码住。 关键词:数据集 机器翻译 机器视觉 数据集是机器学习模型训练的基础&…...

Logview下载
Logview下载 之前一直用的NotePad 后来偶尔的看到作者有发布不当言论 就卸载了又去下载了NotePad– 但是,其实不管是 还是 – 打开大一些的文件都会卡死 所以就搜了这个logview 用起来还不错,目前我这再大的文件 这个软件都是秒打开 但是也会有一点点小…...
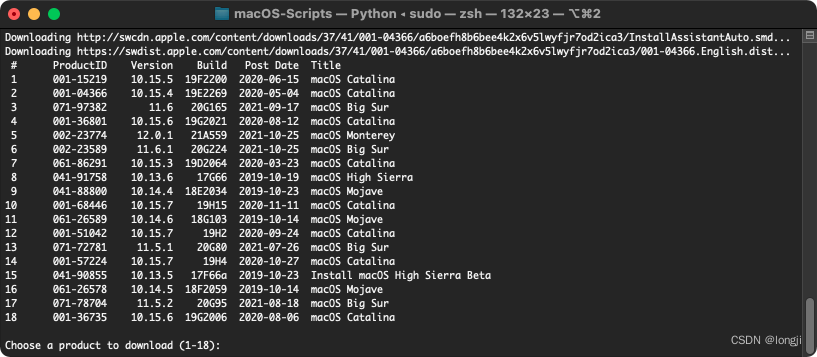
macos 下载 macOS 系统安装程序及安装U盘制作方法
01 下载 macOS 系统安装程序的方法 本文来自: https://discussionschinese.apple.com/docs/DOC-250004259 简介 Mac 用户时不时会需要下载 macOS 的安装程序,目的不同,或者升级或者降级,或者研究或者收藏。为了方便不同用户,除…...
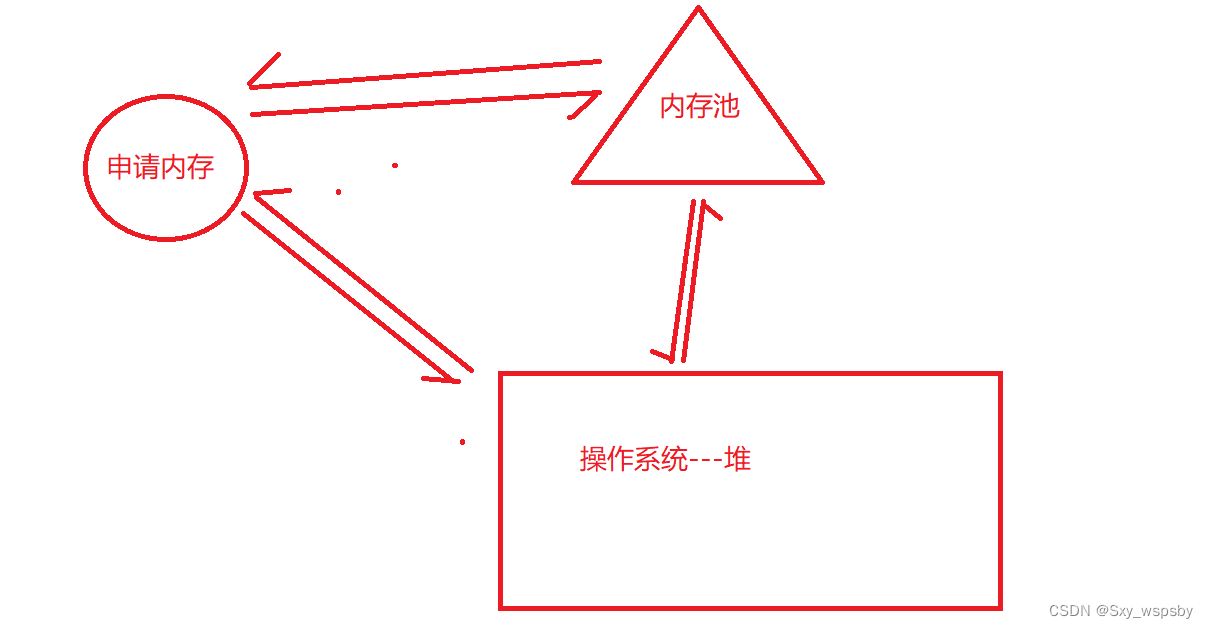
c++动态内存分布以及和C语言的比较
文章目录 前言一.c/c内存分布 C语言的动态内存管理方式 C内存管理方式 operator new和operator delete函数 malloc/free和new/delete的区别 定位new 内存泄漏的危害总结前言 c是在c的基础上开发出来的,所以关于内存管理这一方面是兼容c的&…...

软考高级信息系统项目管理师系列之三十一:项目变更管理
软考高级信息系统项目管理师系列之三十一:项目变更管理 一、项目变更管理内容二、项目变更管理基本概念1.项目变更管理定义2.项目变更产生的原因3.项目变更的分类三、项目变更管理的原则和工作流程1.项目变更管理的原则2.变更管理的组织机构3.变更管理的工作程序四、项目变更管…...
【Vue3源码】第二章 effect功能的完善补充
【Vue3源码】第二章 effect功能的完善补充 前言 上一章节我们实现了effect函数的功能stop和onstop,这次来优化下stop功能。 优化stop功能 之前我们的单元测试中,stop已经可以成功停止了响应式更新(清空了收集到的dep依赖) st…...
)
CHAPTER 2 Web Server - apache(httpd)
Web Server - httpd2.1 http2.1.1 协议版本2.1.2 http报文2.1.3 web资源(web resource)2.1.4 一次完整的http请求处理过程2.1.5 接收请求的模型2.2 httpd配置2.2.1 MPM(多进程处理模块)1. 工作模式2. 切换MPM3. MPM参数配置2.2.2 主配置文件1. 基本配置2. 站点访问控制常见机制…...
【Vagrant】下载安装与基本操作
文章目录概述软件安装安装VirtualBox安装Vagrant配置环境用Vagrant创建一个VMVagrantfile文件配置常用命令概述 Vagrant是一个创建虚拟机的技术,是用来创建和管理虚拟机的工具,本身自己并不能创建管理虚拟机。创建和管理虚拟机必须依赖于其他的虚拟化技…...
常用类(五)System类
(1)System类常见方法和案例: (1)exit:退出当前程序 我们设计的代码如下所示: package com.ypl.System_;public class System_ {public static void main(String[] args) {//exit: 退出当前程序System.out.println("ok1"…...

Navicat Premium 安装 注册
Navicat Premium 一.Navicat Premium的安装 1.暂时关闭windows的病毒与威胁防护弄完再开,之后安装打开过程中弹窗所有警告全部允许,不然会被拦住 2.下载安装包,解压 链接:https://pan.baidu.com/s/1X24VPC4xq586YdsnasE5JA?pwdu4vi 提取码…...
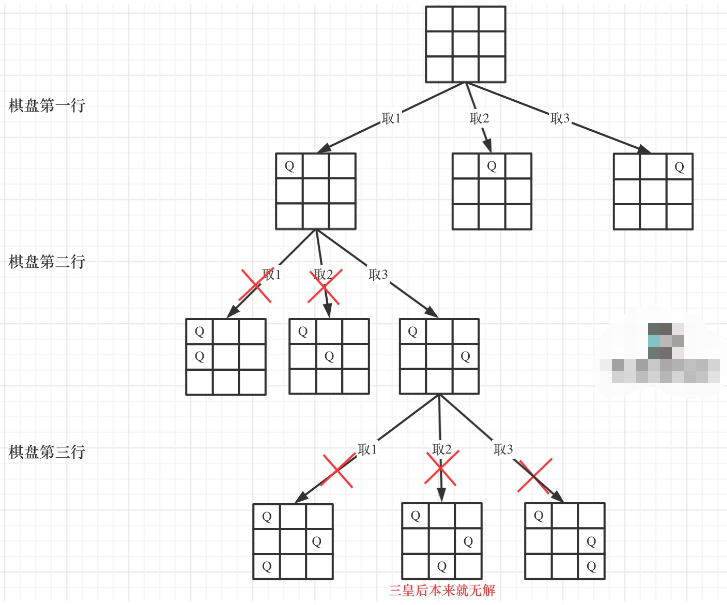
回溯算法总结
首先回溯算法本身还是一个纯暴力的算法,只是回溯过程可能比较抽象,导致大家总是感觉看到的相关题目做的不是很顺畅,回溯算法一般来说解决的题目有以下几类:组合问题:lq77、lq17、lq39、lq40、lq216、切割问题ÿ…...
ccc-pytorch-基础操作(2)
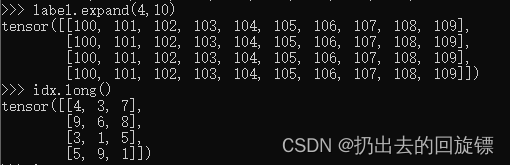
文章目录1.类型判断isinstance2.Dimension实例3.Tensor常用操作4.索引和切片5.Tensor维度变换6.Broadcast自动扩展7.合并与分割8.基本运算9.统计属性10.高阶OP大伙都这么聪明,注释就只写最关键的咯1.类型判断isinstance 常见类型如下: a torch.randn(…...

独居老人一键式报警器
盾王居家养老一键式报警系统,居家养老一键式报警设备 ,一键通紧急呼救设备,一键通紧急呼救系统,一键通紧急呼救器 ,一键通紧急呼救终端,一键通紧急呼救主机终端产品简介: 老人呼叫系统主要应用于…...

软考案例分析题精选
试题一:阅读下列说明,回答问题1至问题4,将解答填入答题纸的对应栏内。某公司中标了一个软件开发项目,项目经理根据以往的经验估算了开发过程中各项任务需要的工期及预算成本,如下表所示:任务紧前任务工期PV…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...
