C#设计模式之--六大原则 开闭原则
设计模式六大原则是单一职责原则、里氏替换原则、依赖倒置原则、接口隔离原则、迪米特法则、开闭原则。它们不是要我们刻板的遵守,而是根据实际需要灵活运用。只要对它们的遵守程度在一个合理的范围内,努为做到一个良好的设计。本文主要介绍一下.NET(C#) 开闭原则。
开闭原则(Open Closed Principle)
开闭原则(Open-Closed Principle,OCP)是指一个软件实体(如类、模块和函数)应该对扩展开放,对修改关闭。如当一个模块需要修改的时,不应该直接修改源代码,这样有可能对现有的工作造成影响。应该通过拓展来实现新需求。
例如,
1)一般的反面设计实现
using System;
namespace ConsoleApplication
{/// <summary>/// 矩形(Shape.cs)/// </summary>public class Shape{private double _width;private double _height;private double _radius;private string _name;public Shape(string name, double width, double height){this._width = width;this._height = height;_name = name;}public double AreaRectangle(){return _width * _height;}public void DisplayRectangle(){Console.WriteLine("{0} 长:{1},宽:{2},面积:{3}", _name, _width, _height, this.AreaRectangle());}public Shape(string name, double radius){this._radius = radius;this._name = name;}public double AreaCircle(){return Math.Round(Math.PI * _radius * _radius);}public void DisplayCircle(){Console.WriteLine("{0} 半径:{1},面积:{2}", _name, _radius, this.AreaCircle());}}class Program{static void Main(string[] args){Shape circle = new Shape("圆", 1);circle.DisplayCircle();Shape rectangle = new Shape("正方形", 100, 100);rectangle.DisplayRectangle();Console.ReadKey();}}
}2)开闭原则的实现
using System;
namespace ConsoleApplication
{//Shape.cspublic abstract class Shape{protected string _name;public Shape(string name){this._name = name;}/// <summary>/// 面积/// </summary>/// <returns></returns>public abstract double Area();/// <summary>/// 显示/// </summary>public abstract void Display();}/// <summary>/// 矩形(Rectangle.cs)/// </summary>public class Rectangle : Shape{private double _width;private double _height;public Rectangle(string name, double width, double height): base(name){this._width = width;this._height = height;}public override double Area(){return _width * _height;}public override void Display(){Console.WriteLine("{0} 长:{1},宽:{2},面积:{3}", _name, _width, _height, this.Area());}}/// <summary>/// 圆形(Circle.cs)/// </summary>public class Circle : Shape{private double _radius;public Circle(string name, double radius): base(name){this._radius = radius;}public override double Area(){return Math.Round(Math.PI * _radius * _radius);}public override void Display(){Console.WriteLine("{0} 半径:{1},面积:{2}", _name, _radius, this.Area());}}class Program{static void Main(string[] args){ Shape circle = new Circle("圆", 1);circle.Display();Shape rectangle = new Rectangle("正方形", 100, 100);rectangle.Display();Console.ReadKey();}}
}
相关文章:

C#设计模式之--六大原则 开闭原则
设计模式六大原则是单一职责原则、里氏替换原则、依赖倒置原则、接口隔离原则、迪米特法则、开闭原则。它们不是要我们刻板的遵守,而是根据实际需要灵活运用。只要对它们的遵守程度在一个合理的范围内,努为做到一个良好的设计。本文主要介绍一下.NET(C#)…...
编写Dockerfile制作自己的镜像并推送到私有仓库
说明:我将用到的私有仓库是Harbor,安装教程参考我的这一篇文章: 安装搭建私有仓库Harbor_Word_Smith_的博客-CSDN博客 一、案例1 1、要求 编写Dockerfile制作Web应用系统nginx镜像,生成镜像nginx:v1.1,并推送其到私…...

华为OD-分积木/分苹果
题目描述 哥哥弟弟分一堆积木,每块积木重量不同。弟弟要求平分两组,每组数量可以不同但总重量必须相等。 然而弟弟只会二进制并且加法不进位。例如三块积木 3,5,6 分成两组 [3] 和 [5,6] 弟弟认为 5(二进制1001)加上6(…...

Mysql的引擎有哪些?支持事物么?DB储存引擎有哪些?
Mysql的引擎有哪些?支持事物么?DB储存引擎有哪些? MySQL有多种存储引擎,每种存储引擎有各自的优缺点,可以择优选择使用: MyISAM、InnoDB、MERGE、MEMORY(HEAP)、BDB(BerkeleyDB)、EXAMPLE、FEDERATED、ARCH…...

【懒加载】js实现懒加载、vue实现图片懒加载指令
懒加载 延迟加载,对于一个很长的页面,优先加载可视区域的内容,其他部分等进入可视区域时再加载 懒加载作用 是一种网页性能优化的方式,它能极大的提升用户体验。比如一个页面中有很多图片,但是首屏只出现几张&#…...
)
微信小程序教学系列(7)
第七章:小程序安全和权限管理 第一节:小程序安全性保障 在开发小程序时,我们要时刻牢记小程序的安全性。毕竟,我们可不希望我们的小程序被黑客入侵或者用户的隐私被泄露。所以,让我们一起来了解一下如何保障小程序的…...

Android 9.0 kenel和frameworks中修改ram运行内存的功能实现
1.前言 在9.0的系统rom产品开发定制中,在对一些产品开发中的配置需求方面,在产品后续订单中,在某些机型中需要升级下系统内核配置,项目时间比较仓促,所以 来不及对硬件重新定制,就需要软件方面在ram运行内存的容量大小方面作假,修改ram真实的大小容量,所以就需要在ken…...

PHP实践:获取网络上图片的长宽以及图片类型
🏆作者简介,黑夜开发者,全栈领域新星创作者✌,CSDN博客专家,阿里云社区专家博主,2023年6月CSDN上海赛道top4。 🏆数年电商行业从业经验,历任核心研发工程师,项目技术负责…...

使用 DPO 微调 Llama 2
简介 基于人类反馈的强化学习 (Reinforcement Learning from Human Feedback,RLHF) 事实上已成为 GPT-4 或 Claude 等 LLM 训练的最后一步,它可以确保语言模型的输出符合人类在闲聊或安全性等方面的期望。然而,它也给 NLP 引入了一些 RL 相关…...
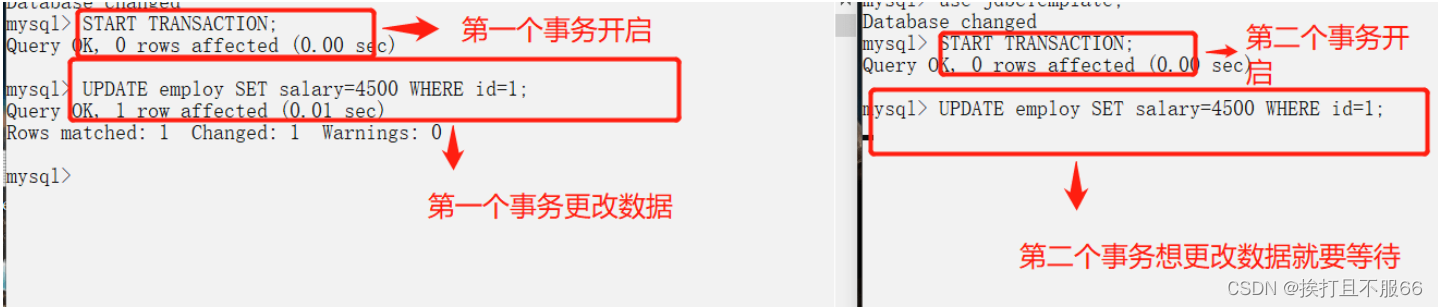
数据库——事务,事务隔离级别
文章目录 什么是事务?事务的特性(ACID)并发事务带来的问题事务隔离级别实际情况演示脏读(读未提交)避免脏读(读已提交)不可重复读可重复读防止幻读(可串行化) 什么是事务? 事务是逻辑上的一组操作,要么都执行,要么都不执行。 事务最经典也经常被拿出…...
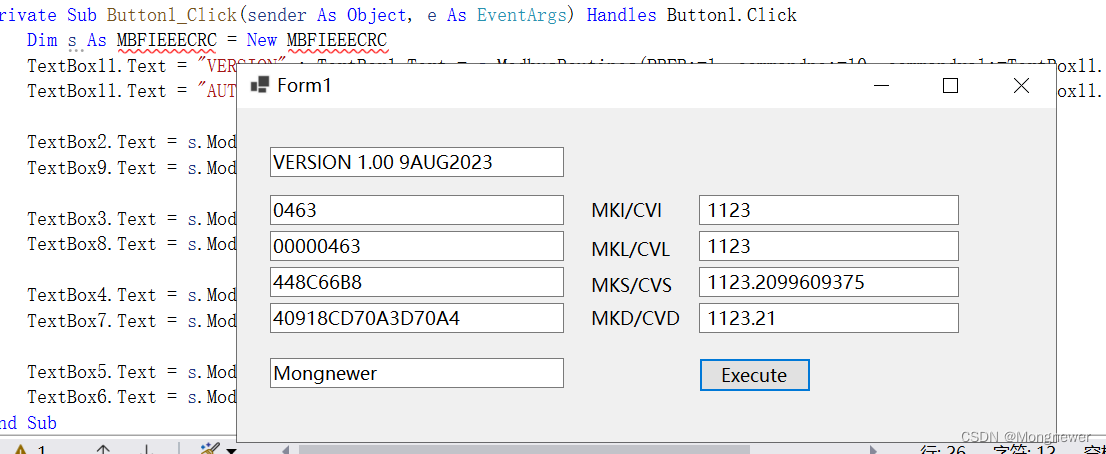
对《VB.NET通过VB6 ActiveX DLL调用PowerBasic及FreeBasic动态库》的改进
《VB.NET通过VB6 ActiveX DLL调用PowerBasic及FreeBasic动态库》使用的Activex DLL公共对象是需要先注册的。https://blog.csdn.net/weixin_45707491/article/details/132437502?spm1001.2014.3001.5501 Activex DLL事前注册,一次多用说起来也不是啥大问题&#x…...

【PHP】数据类型运算符位运算
文章目录 数据类型简单(基本)数据类型:4个小类复合数据类型:2个小类特殊数据类型:2个小类类型转换类型判断整数类型浮点类型布尔类型 运算符赋值运算符算术运算符比较运算符逻辑运算符连接运算符错误抑制符三目运算符自…...

使用 Nacos 作为 Spring Boot 配置中心
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...
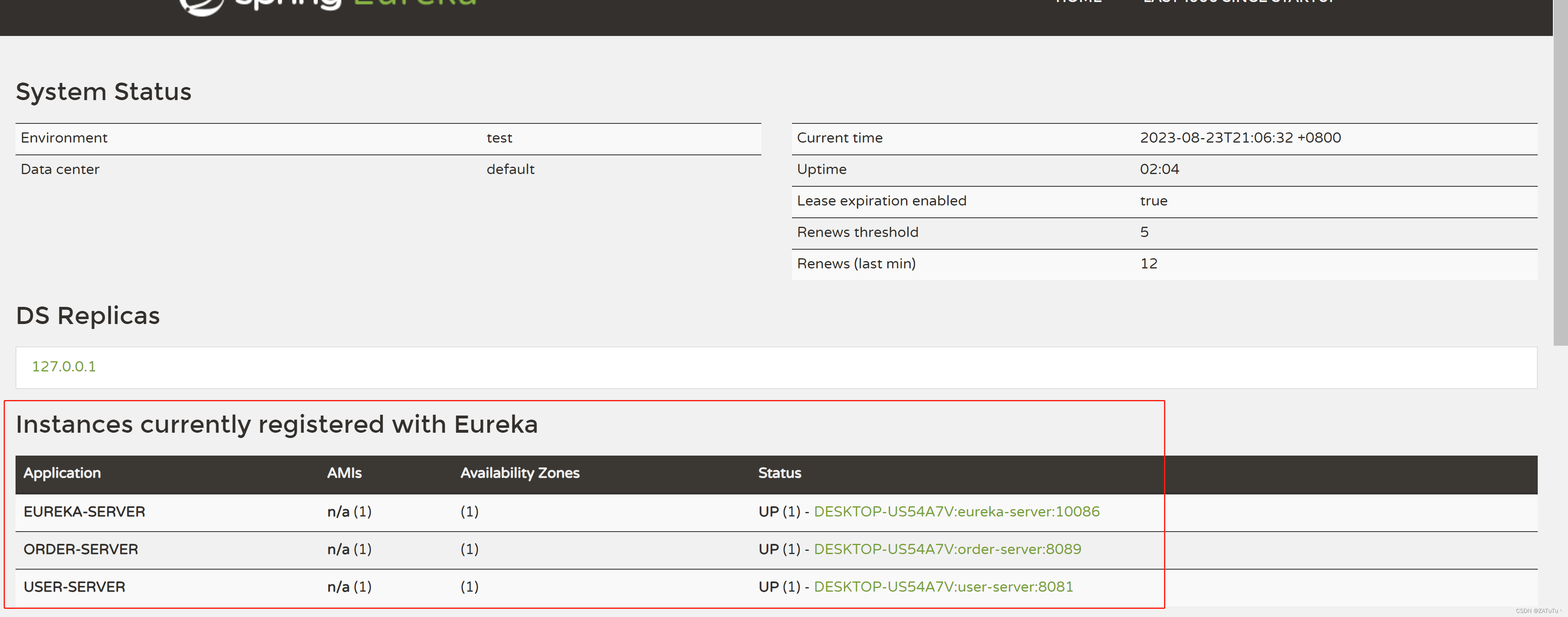
微服务 Eureka
Eureka Eureka是Netflix开源的一个用于构建基于微服务架构的服务发现和注册中心技术。在微服务架构中,系统被拆分成多个小型、自治的服务,每个服务负责特定的业务功能。这些服务需要能够相互发现和通信,这就是Eureka所提供的功能。 Eureka主…...

Spring Boot 事务和事务传播机制
1. 为什么需要事务? 事务定义 将一组操作封装成一个执行单元 (封装到一起),这一组的执行具备原子性, 那么就要么全部成功,要么全部失败. 为什么要用事务? 比如转账分为两个操作: 第一步操作:A 账户-100 元。 第二步操作:B账户 100 元。 如果没有事务&a…...

计算机组成原理(巨巨巨基础篇)
有关《计算机组成原理》课本中有关 内存计算换算(字,位,字节) 个人理解 前面知识点搭建框架,最后两道例题是直观理解体会 主存储器的基本概念 位:存储信息的最小单位,称为存储位或存储元。 背…...

C语言:选择+编程(每日一练Day7)
目录 选择题: 题一: 题二: 题三: 题四: 题五: 编程题: 题一:图片整理 思路一: 思路二: 题二:寻找数组的中心下标 思路一࿱…...

leetcode做题笔记93. 复原 IP 地址
有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 . 分隔。 例如:"0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址,但是 "0.011.255.2…...

HTTPS 中间人攻击
HTTPS 中间人攻击 中间人攻击过程 通讯过程 客户端——中间人——服务器 过程如下 服务器向客户端发送公钥攻击者截获公钥,保留在自己手上然后攻击者自己生成一个【伪造的】公钥,发给客户端客户端收到【伪造的】公钥后,利用【伪造的】公…...
MATLAB打开excel读取写入操作例程
本文使用素材含代码测试用例等 MATLAB读写excel文件历程含,内含有测试代码资源-CSDN文库 打开文件 使用uigetfile函数过滤非xlsx文件,找到需要读取的文件,首先判断文件是否存在,如果文件不存在,程序直接返回&#x…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...
