看见统计——第四章 统计推断:频率学派
看见统计——第四章 统计推断:频率学派
接下来三节的主题是中心极限定理的应用。在不了解随机变量序列 {Xi}\{X_i\}{Xi} 的潜在分布的情况下,对于大样本量,中心极限定理给出了关于样本均值的声明。例如,如果 YYY 是一个 N(0,1)N(0,1)N(0,1) 随机变量,并且{Xi}\{X_i\}{Xi}的独立同分布具有平均值 μμμ 和方差 σ2σ^2σ2,那么
P(X‾−μσ/n∈A)≈P(Y∈A)P(\frac{\overline{X}-\mu}{\sigma /\sqrt{n}}\in A)\approx P(Y\in A) P(σ/nX−μ∈A)≈P(Y∈A)
特别是,如果我们想要一个 YYY 以概率 0.950.950.95 落点的区间,我们可以在网上或书中查找 zzz 表,,对于 N(0,1)N(0,1)N(0,1) 随机变量 YYY ,
P(Y∈(−1.96,1.96))=P(−1.96≤Y≤1.96)=0.95P(Y\in(-1.96,1.96))=P(-1.96\le Y\le 1.96) = 0.95 P(Y∈(−1.96,1.96))=P(−1.96≤Y≤1.96)=0.95
由于X‾−μσ/n\frac{\overline{X}-\mu}{\sigma /\sqrt{n}}σ/nX−μ 接近于 N(0,1)N(0,1)N(0,1) ,这意味着
P(−1.96≤X‾−μσ/n≤1.96)=0.95P(-1.96\le \frac{\overline{X}-\mu}{\sigma /\sqrt{n}}\le 1.96) = 0.95 P(−1.96≤σ/nX−μ≤1.96)=0.95
从上述声明中,我们可以对实验进行陈述,以量化置信度,接受或拒绝假设。
置信区间Confidence Intervals
假设在美国总统选举期间,我们对倾向于支持希拉里而非特朗普的人所占的比例 ppp 感兴趣。我们可以打电话给这个国家的每个人,记录他们支持的人,这种做法显然不现实。相反,我们可以取一堆样本X1,⋯,XnX_1,\cdots,X_nX1,⋯,Xn,其中
Xi={1第i个人更支持希拉里0其它X_i=\begin{cases} 1& 第i个人更支持希拉里\\ 0& 其它 \end{cases} Xi={10第i个人更支持希拉里其它
那么样本均 X‾=1n∑i=1nXi\overline{X}=\frac{1}{n}\sum_{i=1}^{n}X_iX=n1∑i=1nXi 就是我们样本中偏爱希拉里的比例。假设 ppp 是更喜欢希拉里的真实比例( ppp 未知)。注意E(X‾)=pE(\overline{X})=pE(X)=p。然后通过 CLTCLTCLT(中心极限定理),
X‾−μσ/n∼N(0,1)\frac{\overline{X}-\mu}{\sigma /\sqrt{n}} \sim N(0,1) σ/nX−μ∼N(0,1)
由于我们不知道 σσσ 的真实值,我们使用样本方差来估计它,定义如下:
S2≐1n−1∑i=1n(Xi−X‾)2S^2\doteq \frac{1}{n-1}\sum_{i=1}^{n}(X_i-\overline{X})^2 S2≐n−11i=1∑n(Xi−X)2
这是 σ2σ^2σ2 的一致估计量,因此当 nnn 很大时,它与真方差 σ2σ^2σ2 相差很大的概率很小。因此,我们可以将表达式中的σσσ 替换为 S=1n−1∑i=1n(Xi−X‾)2S= \sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(X_i-\overline{X})^2}S=n−11∑i=1n(Xi−X)2。由于X‾−μS/n\frac{\overline{X}-\mu}{S /\sqrt{n}}S/nX−μ 接近于 N(0,1)N(0,1)N(0,1) ,这意味着
P(−1.96≤X‾−μS/n≤1.96)=0.95P(-1.96\le \frac{\overline{X}-\mu}{S /\sqrt{n}}\le 1.96) = 0.95 P(−1.96≤S/nX−μ≤1.96)=0.95
重新排列 ppp 的表达式,我们有
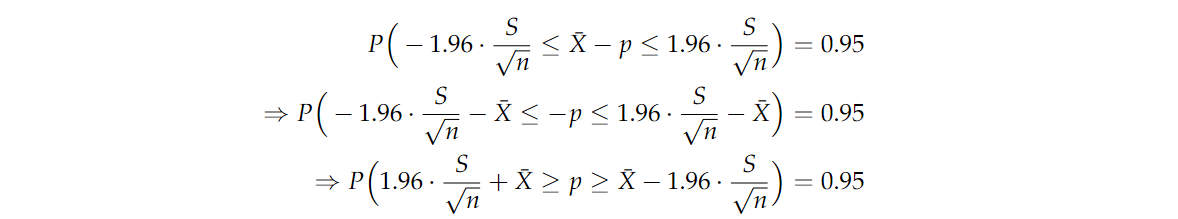
即使我们不知道 ppp 的真实值,我们可以从上面的表达式得出结论, ppp 有0.95的概率在如下区间中:
(X‾−1.96⋅Sn,X‾+1.96⋅Sn)(\overline{X}-1.96 \cdot \frac{S}{\sqrt{n}},\overline{X}+1.96 \cdot \frac{S}{\sqrt{n}}) (X−1.96⋅nS,X+1.96⋅nS)
这被称为参数 ppp 的95%的置信度区间。此近似适用于较大的 nnn 值,通常要确保 n>30n>30n>30 。可视化如下:

假设检验Hypothesis Testing
让我们回到2016年总统选举中决定选民偏好的例子。假设我们怀疑支持希拉里的选民比例大于1/21/21/2 ,并且我们从美国人口中抽取了标记为 {Xi}in=1\{X_i\}^n_i=1{Xi}in=1的样本。基于这些样本,我们能支持或否定希拉里更受欢迎的假设吗?我们对我们的结论有多大的信心?假设检验是帮助回答这些问题的完美工具。
构建一个测试
本文中的假设是关于感兴趣的参数的声明。在总统选举的例子中,感兴趣的参数是 ppp ,即支持希拉里的人所占的比。那么一个假设可能是 p>0.5p>0.5p>0.5 ,即超过一半的人支持希拉里。
假设检验有四个主要组成部分。
-
备择假设alternative hypothesis,表示为HaH_aHa ,是一个我们想要支持的主张。在前面的例子中,备择假设为 p>0.5p>0.5p>0.5 。
-
零假设null hypothesis,记为 H0H_0H0,与备择假设相反。在这种情况下,零假设是 p≤0.5p≤0.5p≤0.5 ,即只有不到一半的人支持希拉里。
-
检验统计量test statistic,是样本观测值的函数。基于检验统计量,我们将接受或拒绝零假设。在前面的例子中,检验统计量是样本均值 X‾\overline{X}X 。样本均值通常是许多假设检验的检验统计量。
-
拒绝域rejection region是样本空间 ΩΩΩ 的子集,它决定是否拒绝零假设。如果检验统计量落在拒绝域,那么我们拒绝原假设。否则,我们接受。在总统选举的例子中,拒绝区域为
RR:{(x1,x2,...,xn):X‾>k}RR:\{(x_1,x_2,...,x_n):\overline{X}>k\} RR:{(x1,x2,...,xn):X>k}
这种表示法意味着如果 X‾\overline{X}X 落在区间 (k,∞)(k,∞)(k,∞),我们将拒绝,其中 kkk 是我们必须确定的某个数字。kkk由Type I error决定,它在下一节中定义。一旦计算出 kkk ,我们根据检验统计量的值拒绝或接受零假设,检验完成。
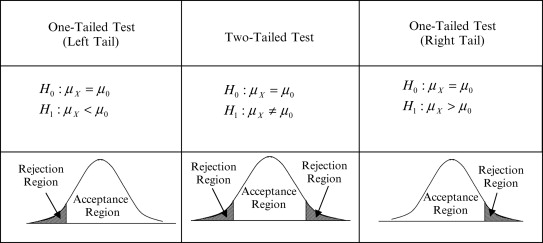
错误类型
在假设检验中有两种基本类型的错误。它们分别表示为 III 型和 IIIIII 型错误。
🔥 定义 :当 H0H_0H0 实际上为真,我们却拒绝它时,就犯了 III 型错误。Type I error的概率通常记为 ααα。
换句话说,ααα 是假阳性的概率。
🔥 定义 :当 H0H_0H0 实际上为假,我们却接受它时,就犯了 IIIIII 型错误。Type II error的概率通常记为 βββ。
换句话说, βββ 是假阴性的概率。
在假设检验的背景下, ααα 将决定拒绝域。如果我们将假阳性的概率限制在小于0.05,那么我们有
P(X‾∈RR∣H0)≤0.05P(\overline{X}\in RR|H_0)\le 0.05 P(X∈RR∣H0)≤0.05
即假设 H0H_0H0 为真,我们的检验统计量落在拒绝域(意味着我们拒绝 H0H_0H0 ),概率为0.05。继续我们的总统选举的例子,拒绝域的形式是 X‾>k\overline{X} > kX>k,零假设是 p≤0.5p≤0.5p≤0.5。我们上面的表达式就变成了
P(X‾>k∣p≤5)≤0.05P(\overline{X}>k|p\le 5)\le 0.05 P(X>k∣p≤5)≤0.05
如果 n>30n>30n>30 ,那我们可以应用中心极限定理
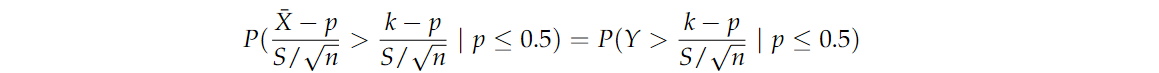
其中 YYY 是 N(0,1)N(0,1)N(0,1) 的随机变量。由于 p≤0.5p≤0.5p≤0.5 意味着 k−pS/n≥k−0.5S/n\frac{k-p}{S/\sqrt{n}} \ge \frac{k-0.5}{S/\sqrt{n}}S/nk−p≥S/nk−0.5,我们也必须有
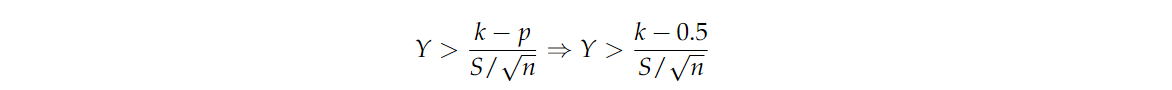
因此

因此,如果我们将不等式右侧的概率限定为0.05,那么我们也将不等式左侧的概率(I型误差 ααα )限定为0.05。由于 YYY 是 N(0,1)N(0,1)N(0,1) 的随机变量,我们可以查 zzz 表,找到 z0.05=−1.64z_{0.05} =−1.64z0.05=−1.64,因此
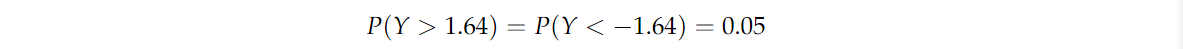
设k−0.5S/n=1.64\frac{k-0.5}{S/\sqrt{n}}=1.64S/nk−0.5=1.64,我们可以求解 kkk 来确定拒绝域:
k=0.5+1.64⋅Snk=0.5+1.64\cdot \frac{S}{\sqrt{n}} k=0.5+1.64⋅nS
由于我们的拒绝域形式为 X‾>k\overline{X} > kX>k,我们只需检查 X‾>0.5+1.64⋅Sn\overline{X} > 0.5+1.64\cdot \frac{S}{\sqrt{n}}X>0.5+1.64⋅nS。如果这是真的,那么我们拒绝零假设,并得出结论,超过一半的人口支持希拉里。因为我们设 α=0.05α = 0.05α=0.05 ,所以我们有 1−α=0.951−α = 0.951−α=0.95 的把握相信我们的结论是正确的。
在上面的例子中,我们通过为 ppp 代入0.5来确定拒绝域,即使零假设为 p≤0.5p≤0.5p≤0.5 。这就好像我们的零假设是H0:p=0.5H_0: p = 0.5H0:p=0.5,而不是H0:p≤0.5H_0: p≤0.5H0:p≤0.5。一般来说,当我们确定拒绝域时,可以简化 H0H_0H0 ,并假设边界情况(在这种情况下 p=0.5p = 0.5p=0.5)。
p-Values
正如我们在上一节中看到的,选定的 ααα 确定了拒绝域,因此假阳性的概率小于 ααα 。现在假设我们观察一些检验统计数据,比如说,支持希拉里的选民 X‾\overline{X}X 的样本比例。然后,我们提出以下问题。给定 X‾\overline{X}X,使我们仍然拒绝零假设的 ααα 的最小值是多少?这将引出以下定义。
p=min{α∈(0,1):Reject H0using an α level test}p =\min\{\alpha \in(0,1):\text{Reject}\ H_0\ \text{using an α level test}\} p=min{α∈(0,1):Reject H0 using an α level test}
ppp 值即我们仍然拒绝零假设的 ααα 的最小值。
下面我们通过一个例子来说明。
🍌 假设我们对 nnn 个人进行抽样,问他们更喜欢哪个候选人。就像我们之前做的那样,我们可以将每个人表示为一个指标函数,
Xi={1第i个人更支持希拉里0其它X_i=\begin{cases} 1& 第i个人更支持希拉里\\ 0& 其它 \end{cases} Xi={10第i个人更支持希拉里其它
那么 X‾\overline{X}X 是样本中倾向于希拉里的比例。在取了 nnn 个样本后,假设我们观察到 X‾=0.7\overline{X}=0.7X=0.7 。如果我们要建立一个假设检验,我们的假设,检验统计量和拒绝域将是
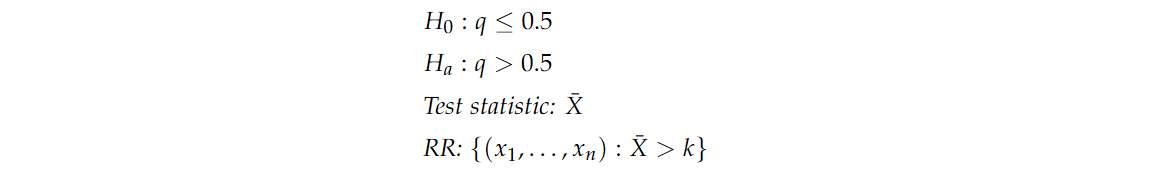
其中 qqq 是整个美国人口中支持希拉里的真实比例。使用直观的定义,ppp 值是我们观察到比 0.70.70.7 更极端的概率。由于零假设是 q≤0.5q≤0.5q≤0.5 ,在这种情况下,"更极端” 意味着 “大于0.7”。因此,ppp 值是指在给定一个新的样本时,我们观察到新 X‾\overline{X}X 大于0.7的概率,假设无效,即 q≤0.5q≤0.5q≤0.5。 X‾\overline{X}X 归一化有
P(X‾>0.7∣H0)=P(X‾−0.5S/n>0.7−0.5S/n)≈P(Y>0.7−0.5S/n)≐pP( \overline{X}>0.7|H_0 )=P(\frac{\overline{X}-0.5}{S/\sqrt{n}}>\frac{0.7-0.5}{S/\sqrt{n}})\approx P(Y>\frac{0.7-0.5}{S/\sqrt{n}})\doteq p P(X>0.7∣H0)=P(S/nX−0.5>S/n0.7−0.5)≈P(Y>S/n0.7−0.5)≐p
其中 Y∼N(0,1)Y\sim N(0,1)Y∼N(0,1)。然后,我们将计算值 zp≐0.7−0.5S/nz_p\doteq \frac{0.7-0.5}{S/\sqrt{n}}zp≐S/n0.7−0.5。然后,我们将查找 zzz 表并找到与 zpz_pzp 对应的概率,记为 ppp (就是我们的 ppp 值)。
Bootstrap
Bootstrap又称自展法、自举法、自助法、靴带法 , 是统计学习中一种重采样(Resampling)技术,用来估计标准误差、置信区间和偏差
Bootstrap是现代统计学较为流行的一种统计方法,在小样本时效果很好。机器学习中的Bagging,AdaBoost等方法其实都蕴含了Boostrap的思想,在集成学习的范畴里 Bootstrap直接派生出了Bagging模型.
子样本之于样本,可以类比样本之于总体

参考
- https://github.com/seeingtheory/Seeing-Theory
- 统计学中的Bootstrap方法(Bootstrap抽样)
相关文章:

看见统计——第四章 统计推断:频率学派
看见统计——第四章 统计推断:频率学派 接下来三节的主题是中心极限定理的应用。在不了解随机变量序列 {Xi}\{X_i\}{Xi} 的潜在分布的情况下,对于大样本量,中心极限定理给出了关于样本均值的声明。例如,如果 YYY 是一个 N(0&am…...
2023年2月访问学者博士后热门国家出入境政策变化汇总
近期关于出国的咨询量日益增多,出入境政策也是其中之一。所以本期知识人网小编汇总了最新访问学者和博士后关注的热门国家及地区入境政策变化,提供给大家。目前各国入境政策大致分为三种:一、 无法入境的国家如:摩洛哥、朝鲜等。二…...

“离开浪浪山”是假象,80%年轻人下班后还在学习,真实是想先上个山。
最近,又有一个关于年轻人与职场的新词横空出世—— 浪浪山。 什么是浪浪山? 每个人心中都有一座浪浪山。 浪浪山,其实是人生的一种状态,步入社会时满腔热血,然而很快就被现实给修理了一顿;想要辞职不干出去…...

Kotlin 33. CompileSdkVersion 和 targetSdkVersion 有什么区别?
CompileSdkVersion 和 targetSdkVersion 有什么区别? 在 build.gradle (Module) 文件中,我们通常会看到 CompileSdkVersion 和 targetSdkVersion 的使用,比如下面是一个完整的 build.gradle (Module) 文件: plugins {id com.and…...

实用调试技巧——“C”
各位CSDN的uu们你们好呀,今天小雅兰的内容是实用调试技巧,其实小雅兰一开始,也不知道调试到底是什么,一遇到问题,首先就是观察程序,改改这里改改那里,最后导致bug越修越多,或者是问别…...
JavaScript - 函数
文章目录一、箭头函数二、函数名三、理解参数3.1 箭头函数中的参数四、没有重载五、默认参数值5.1 默认参数作用域与暂时性死区六、参数扩展与收集6.1 扩展参数6.2 收集参数七、函数声明与函数表达式八、函数作为值九、函数内部9.1 arguments9.2 this9.3 caller9.4 new.target十…...
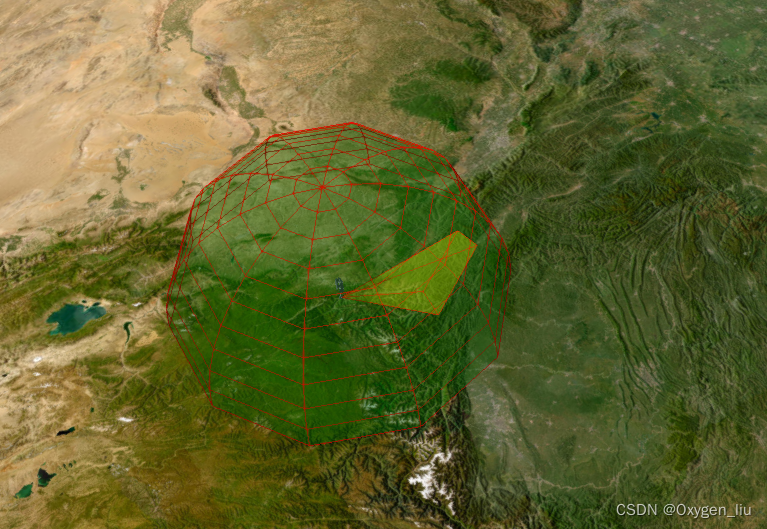
Cesium 卫星轨迹、卫星通信、卫星过境,模拟数据传输。
起因:看了cesium官网卫星通信示例发现只有cmzl版本的,决定自己动手写一个。欢迎大家一起探讨,评论留言。 效果 全部代码在最后 起步 寻找卫星轨迹数据,在网站space-track上找的,自己注册账号QQ邮箱即可。 卫星轨道类…...

2023年湖北中级职称(工程类建筑类)报名条件和要求是什么?
2023年湖北中级职称(工程类建筑类)报名条件和要求是什么? 中级职称分为计算机类、医药类、卫生类、教师类、工程类、经济类等各大类,今天主要就是跟大家说一下工程类中级职称评审的一个条件和要求,这也是评职称人员应该…...

socket编程复习
再次用到socket编程,将socket相关的知识点做了简单整理,根据网络上大家的整理,又做了一些调整和汇总。 API列表 sokect常见的API大致有列表里面这么多,不同平台的实现可能有些微的差别,下面对常用API的参数和用法做了…...
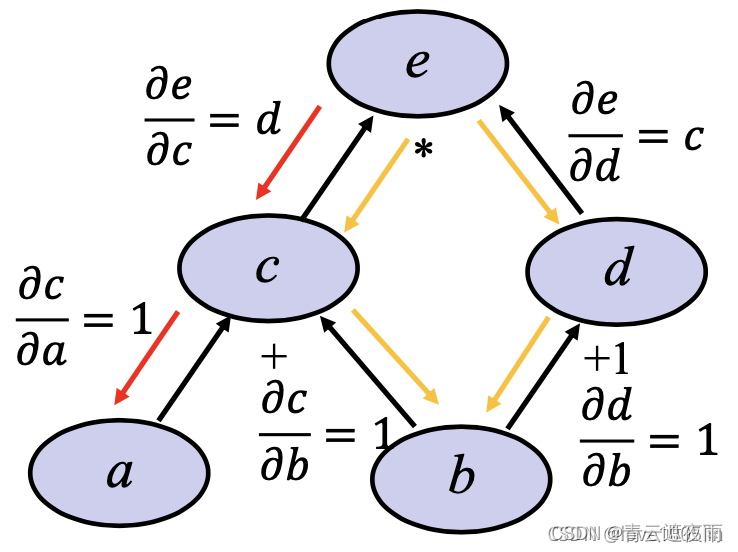
深度学习神经网络基础知识(三)前向传播,反向传播和计算图
专栏:神经网络复现目录 深度学习神经网络基础知识(三) 本文讲述神经网络基础知识,具体细节讲述前向传播,反向传播和计算图,同时讲解神经网络优化方法:权重衰减,Dropout等方法,最后进行Kaggle实…...
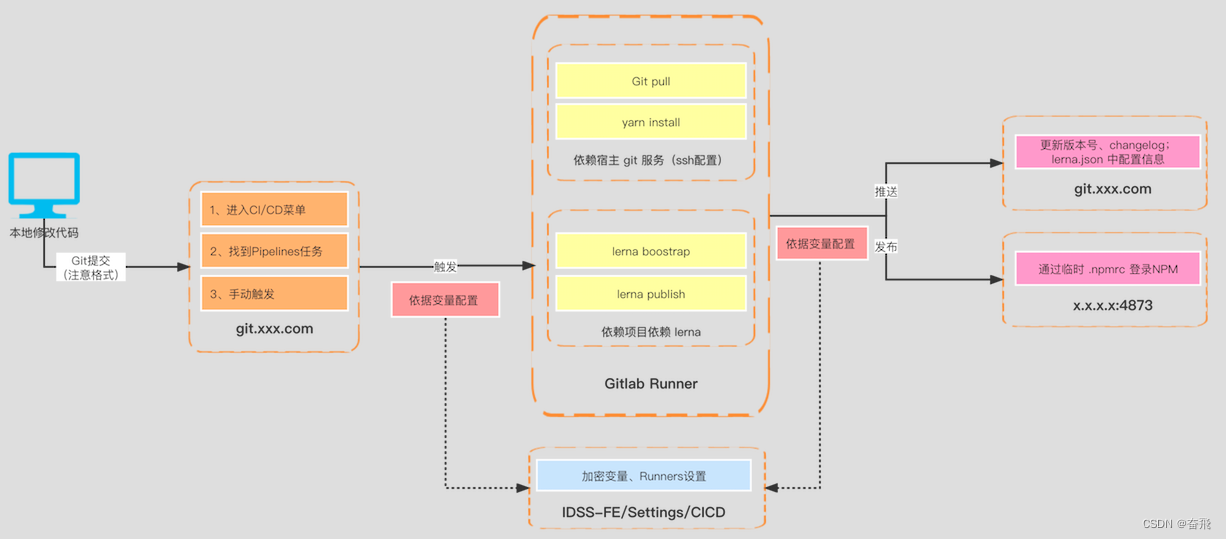
一图说明 monorepo 落地流程方案
关于 monorepo 初次讨论已有2年载,目前团队已经沉淀了成熟的技术方案且经受住了实战考验。所以特梳理相关如下: 也算是关于之前发起的 monorepo–依赖 的解答篇。 上图为目前团队贡献的主流程:① 本地开发 > ② 提交Git仓库 > ③ 触发…...

SAP ABAP WRITE语法大全
列表是ABAP/4报表程序数据的输出媒介。每个ABAP/4报表程序将其输出数据传递到直接与该程序连接的列表中。每个程序最多生成21个列表:1个基本列表和20个辅助列表。 将数据写入列表的基本ABAP/4语句是WRITE、SKIP和ULINE输出语句。 一、标准列表结构 (1&…...

微信小程序自定义全局组件showModal
开发过程中微信提供的showmodal样式不符合ui风格,又不想写成组件用的页面都引入,就考虑模拟showmodal写一个自定义的弹框组件 一,在components中新建一个navModal组件 navModal.wxml <view class="modal_mask" hidden={{hidden}}><view class="mo…...

4|无线传感器网络与应用|无线传感器网络原理及方法-许毅版|考试知识点
《无线传感器网络原理及方法》第1章无线传感器网络概述1.1无线传感器网络的基本概念1.2无线传感器网络的特征1.2.1与现有无线网络的区别1.2.2与现场总线的区别1.2.3传感器节点的限制1.2.4传感器组网的特点1.3无线传感器网络的关键性能指标1.4无线传感器网络的应用1.5无线传感器…...

startForegroundService与startService 使用浅析
一. 了解服务(Service)的概念 service是安卓开发中一个很重要组件,意为“服务”。与我们常见的activity不同,“服务”是默默的在背后进行工作的,通常,它用于在后台为我们执行一些耗时,或者需要…...
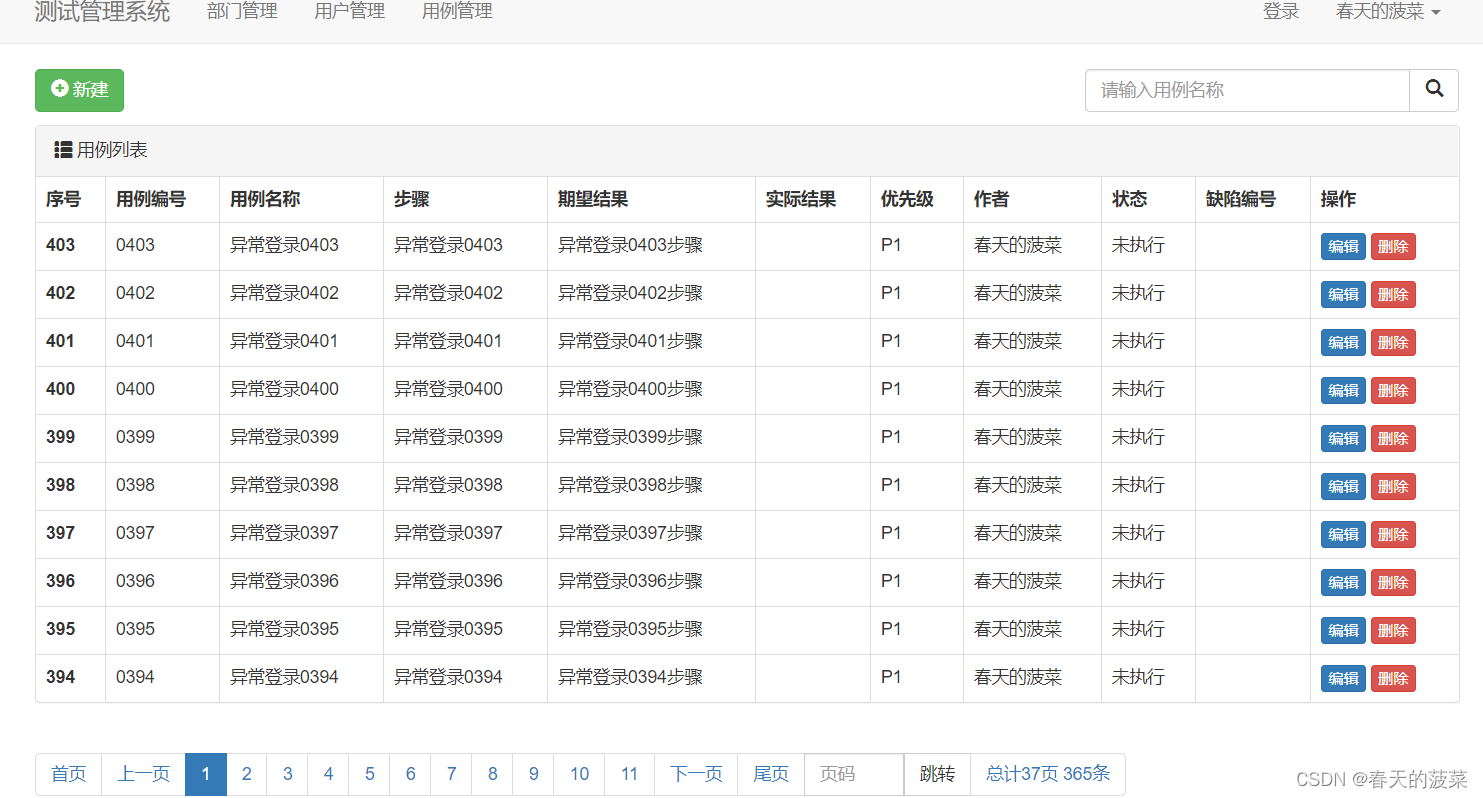
django项目实战三(django+bootstrap实现增删改查)进阶分页
目录 一、分页 1、修改case_list.html页面 2、修改views.py的case_list方法(分页未封装) 二、分页封装 1、新建类Pagination 2、修改views.py的case_list方法 三、再优化,实现搜索分页qing情况 四、优化其他查询页面实现分页和查询 五…...

Python 之 Pandas DataFrame 数据类型的简介、创建的列操作
文章目录一、DataFrame 结构简介二、DataFrame 对象创建1. 使用普通列表创建2. 使用嵌套列表创建3 指定数值元素的数据类型为 float4. 字典嵌套列表创建5. 添加自定义的行标签6. 列表嵌套字典创建 DataFrame 对象7. Series 创建 DataFrame 对象三、DataFrame 列操作1. 选取数据…...
)
华为OD机试真题Python实现【5键键盘的输出】真题+解题思路+代码(20222023)
🔥系列专栏 华为OD机试(Python)真题目录汇总华为OD机试(JAVA)真题目录汇总华为OD机试(C++)真题目录汇总华为OD机试(JavaScript)真题目录汇总文章目录 🔥系列专栏题目输入输出描述:示例1:示例2:解题思路代码实现运行结果:版权说明:题目...
IDEA全家桶式讲解 | IDEA安装、使用、断点调试、Git、插件 (第二篇)
目录 一:JavaEE阶段需要掌握的IDEA技能 1. 配置Tomcat 2. 配置Maven 3. IDEA连接数据库 4. 方便的特殊功能 5. 断点调试(重点) 6. IDEA中常用Git协同开发(重点) 7. 常用插件安装 一:JavaEE阶段需要…...
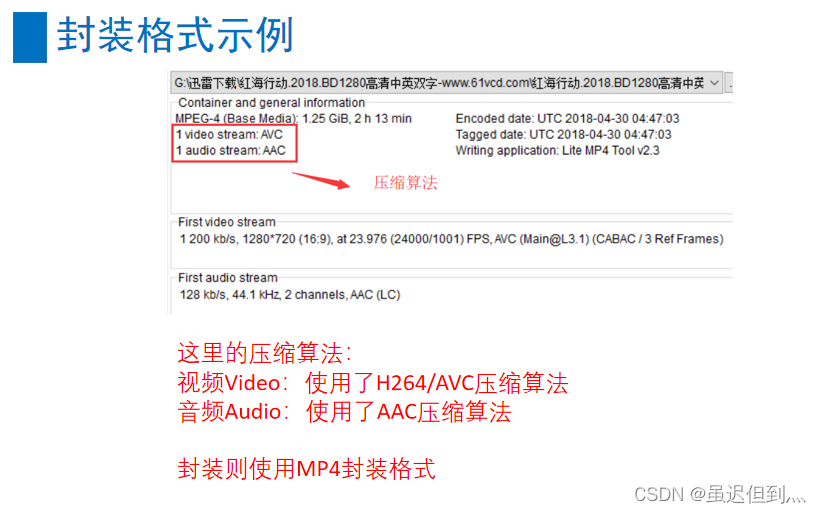
音视频基础之封装格式与音视频同步
封装格式的概念 封装格式(也叫容器)就是将已经编码压缩好的视频流、音频流及字幕按照一定的方案放到一个文件中,便于播放软件播放。 一般来说,视频文件的后缀名就是它的封装格式。 封装的格式不一样,后缀名也就不一样。 比如&a…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
