Ext JS 之Microloader(微加载器)
“Microloader”是 Sencha 数据驱动的 JavaScript 和 CSS 动态加载器的名称。
清单
app.json
用于应用的设置,Sencha Cmd 在构建的时候会读取这个文件。 Sencha Cmd 转换“app.json”的内容并将生成的清单传递给 Microloader 以在运行时使用。 最后,Ext JS 本身也会查阅运行时清单以获取配置选项。
app.json 的内容类似:
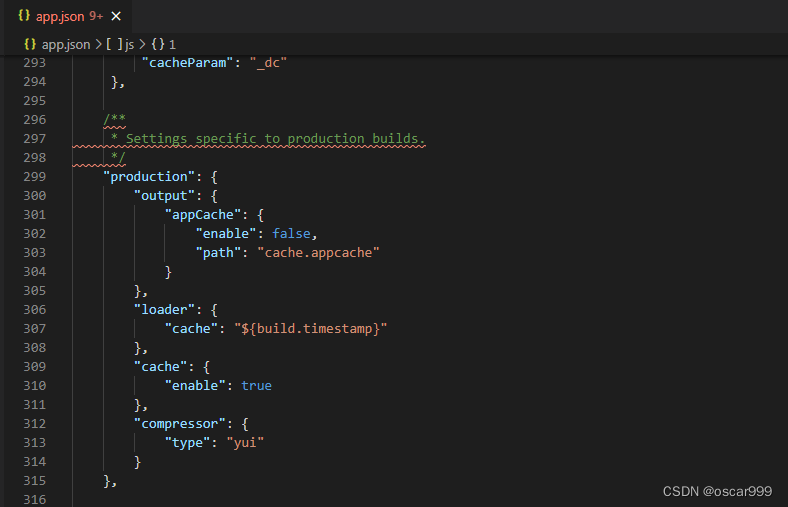
Ext.manifest
启动应用程序时,会发现“app.json”的处理内容加载为“Ext.manifest”。 Ext JS 6 使用指定的 Ext.manifest 属性来执行诸如启用兼容层之类的操作。
<script> 标签
微加载器的使用方式是在页面中加入如下代码:
<script id="microloader" data-app="12345" type="text/javascript" src="bootstrap.js"></script>
默认情况下,此脚本标记将被构建过程替换,但在开发期间用于加载应用程序。 数据应用程序属性应该已在应用程序脚手架期间为您生成。 这是本地存储中使用的唯一ID,用于防止数据冲突。
默认值和自定义
Sencha Cm
相关文章:

Ext JS 之Microloader(微加载器)
“Microloader”是 Sencha 数据驱动的 JavaScript 和 CSS 动态加载器的名称。 清单 app.json 用于应用的设置,Sencha Cmd 在构建的时候会读取这个文件。 Sencha Cmd 转换“app.json”的内容并将生成的清单传递给 Microloader 以在运行时使用。 最后,Ext JS 本身也会查阅运…...

【科研】-- 如何将Endnote中参考文献格式插入到Word?
文章目录 如何将Endnote中参考文献格式插入到Word? 如何将Endnote中参考文献格式插入到Word? 1、首先确保Endnote和Word安装正确,正常可以从学校官网中下载到正版软件,下载后在word栏目中会出现EndNote的标签; 2、可…...

Python爬虫实战案例——第二例
某某美剧剧集下载(从搜索片名开始) 本篇文章主要是为大家提供某些电影网站的较常规的下载电影的分析思路与代码思路(通过爬虫下载电影),我们会从搜索某部影片的关键字开始直到成功下载某一部电影。 地址:aHR0cHM6Ly93d3cuOTltZWlqdXR0LmNvbS9pbmRleC5od…...

深入理解Spring的ImportBeanDefinitionRegistrar接口及其应用
0 导言 ImportBeanDefinitionRegistrar接口在动态注册Bean定义方面发挥着重要作用。本篇博客将深入探讨ImportBeanDefinitionRegistrar接口的作用、用法以及实际应用场景。 1 简介 ImportBeanDefinitionRegistrar接口是Spring Framework中的一个关键接口,位于org…...

【面试题】你理解中JS难理解的基本概念是什么?
前端面试题库 (面试必备) 推荐:★★★★★ 地址:前端面试题库 作用域与闭包 作用域 作用域是当前的执行上下文,值和表达式在其中“可见”或可被访问。如果一个变量或表达式不在当前的作用域中࿰…...
微服务中间件--MQ服务异步通信
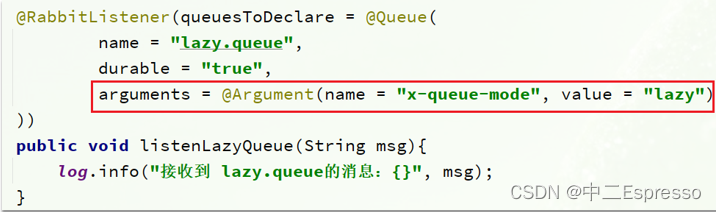
MQ服务异步通信 MQ服务异步通信a.消息可靠性1) 生产者消息确认2) 消息持久化3) 消费者消息确认4) 消费者失败重试4.a) 本地重试4.b) 失败策略 b.死信交换机1) 初识死信交换机2) TTL3) 延迟队列a) 安装延迟队列插件b) SpringAMQP使用延迟队列插件 c.惰性队列1) 消息堆积问题2) 惰…...

爆火「视频版ControlNet」开源了!靠提示词精准换画风,全华人团队出品
“视频版ControlNet”来了! 让蓝衣战神秒变迪士尼公举: 视频处理前后,除了画风以外,其他都不更改。 女孩说话的口型都保持一致。 正在插剑的姜文,也能“下一秒”变猩球崛起了。 这就是由全华人团队打造的最新视频处理…...

常用的数据可视化工具有哪些?要操作简单的
随着数据量的剧增,对分析效率和数据信息传递都带来了不小的挑战,于是数据可视化工具应运而生,通过直观形象的图表来展现、传递数据信息,提高数据分析报表的易读性。那么,常用的操作简单数据可视化工具有哪些࿱…...
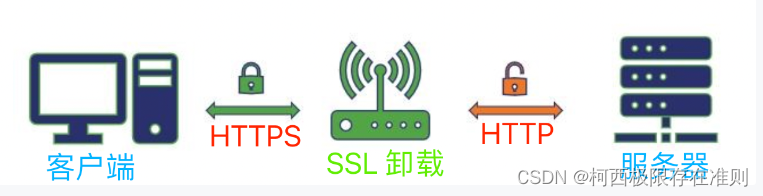
ssl卸载原理
SSL卸载,也称为SSL解密,是一种将SSL加密数据流卸成非加密的明文数据流的过程。SSL卸载通常在负载均衡器、代理服务器、WAF等设备中实现,可以提高传输效率和安全性。 SSL卸载的原理是将SSL数据流拦截下来,通过设备内置的证书进行解…...

【C语言】动态内存管理,详细!!!
文章目录 前言一、为什么存在动态内存分配二、动态内存开辟函数的介绍1.malloc2.calloc3.realloc4.free 三、动态内存开辟中的常见错误1.误对NULL进行解引用操作2.对于动态开辟的空间进行了越界访问3.对于非动态开辟的内存进行了free操作4.只free掉动态开辟内存的一部分5.多次f…...

2023年国赛 高教社杯数学建模思路 - 案例:退火算法
文章目录 1 退火算法原理1.1 物理背景1.2 背后的数学模型 2 退火算法实现2.1 算法流程2.2算法实现 建模资料 ## 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 退火算法原理 1.1 物理背景 在热力学上&a…...
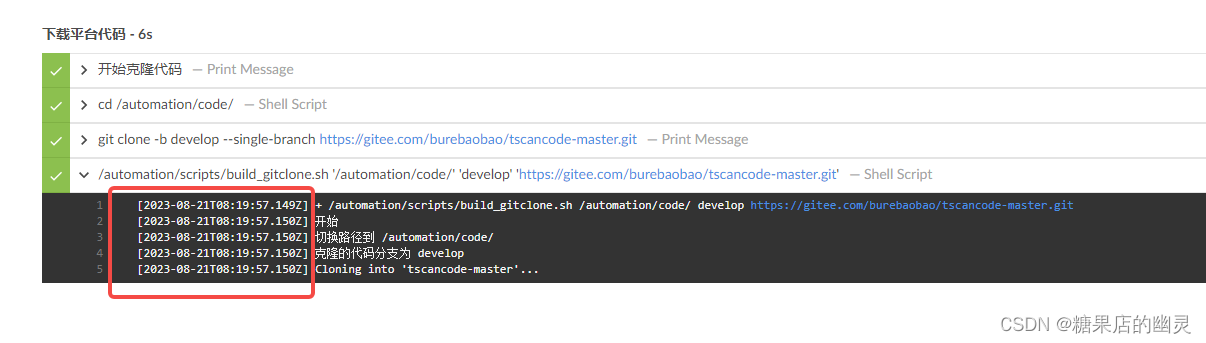
jenkins 日志输出显示时间戳的方式
网上很多方式比较片面,最新版插件直接使用即可无需更多操作。 使用方式如下: 1.安装插件 Timestamper 2.更新全局设置 系统设置-找到 Timestamper 勾选 Enabled for all Pipeline builds 也可修改时间戳格式。 帮助信息中显示 When checked, timesta…...
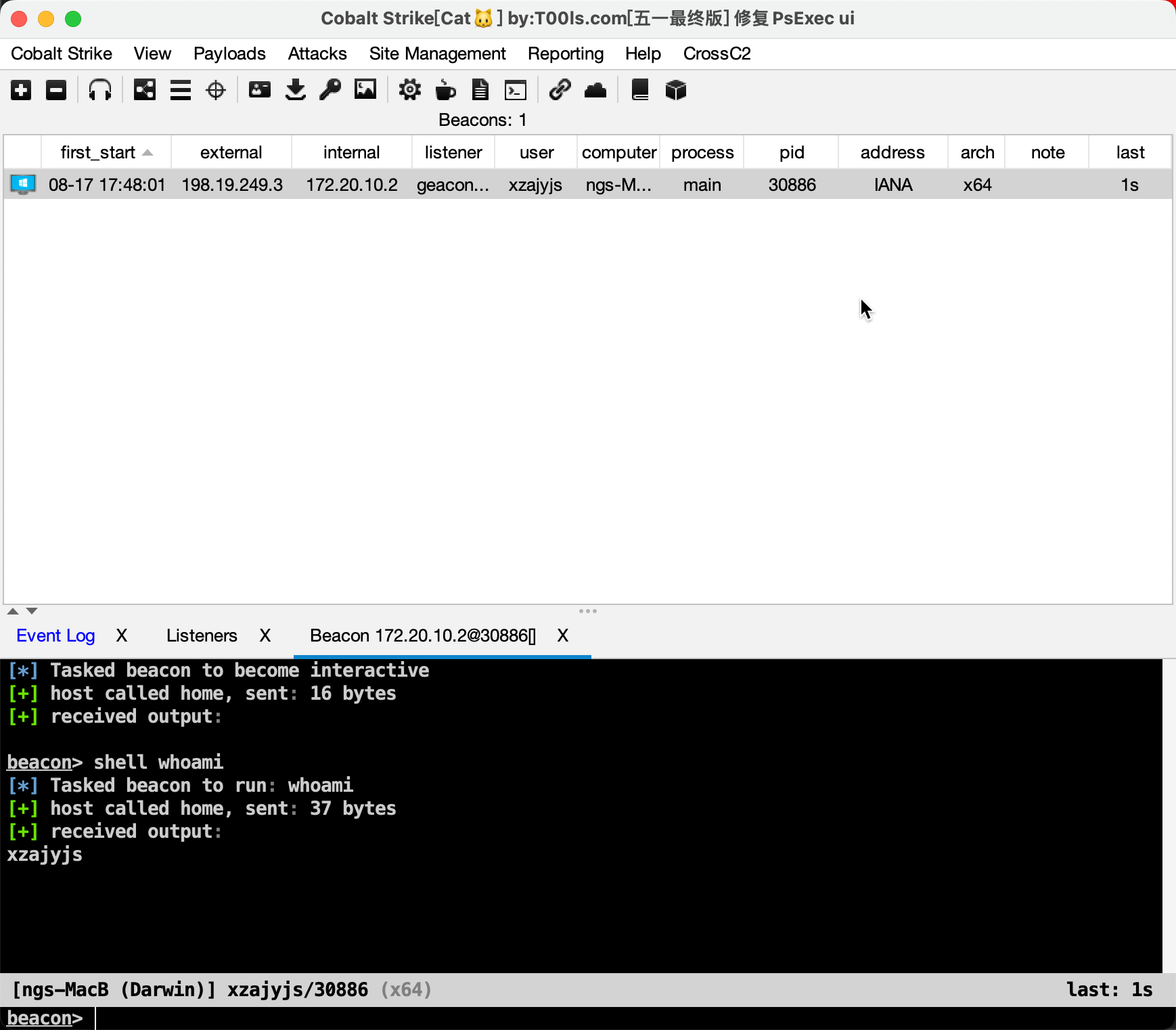
geacon_pro配合catcs4.5上线Mac、Linux
我的个人博客: xzajyjs.cn 一些链接 Try师傅的catcs4.5项目: https://github.com/TryGOTry/CobaltStrike_Cat_4.5,最新版解压密码见:https://www.nctry.com/2708.html geacon_pro: https://github.com/testxxxzzz/geacon_pro BeaconTool.jar: https:/…...
)
vue 实现腾讯地图搜索选点功能(附加搜索联想功能)
注意:开发环境、正式环境需在腾讯地图配置ip地址白名单、域名白名单 封装map组件: <template><iframe width"100%" style"border: none;width: 100%;height: 100%;" :src"map_src"></iframe> </t…...
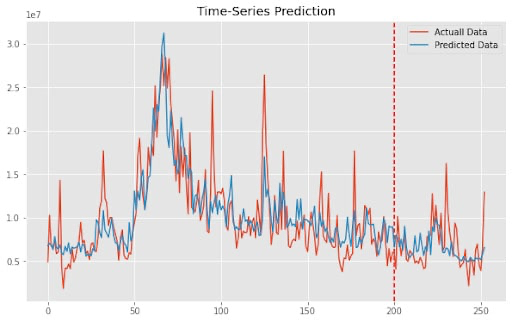
解密长短时记忆网络(LSTM):从理论到PyTorch实战演示
目录 1. LSTM的背景人工神经网络的进化循环神经网络(RNN)的局限性LSTM的提出背景 2. LSTM的基础理论2.1 LSTM的数学原理遗忘门(Forget Gate)输入门(Input Gate)记忆单元(Cell State)…...
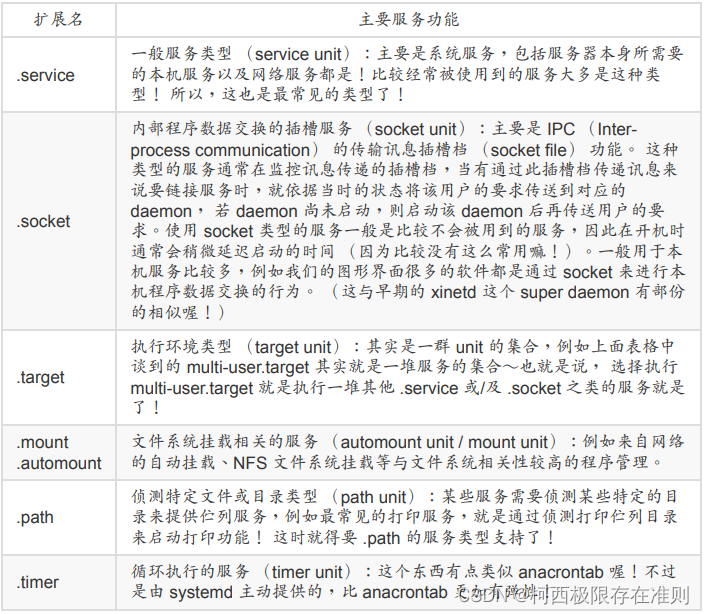
17.1.2 【Linux】systemd使用的unit分类
systemd 有什么好处? 平行处理所有服务,加速开机流程: 旧的 init 启动脚本是“一项一项任务依序启动”的模式,因此不相依的服务也是得要一个一个的等待。但目前我们的硬件主机系统与操作系统几乎都支持多核心架构了,s…...
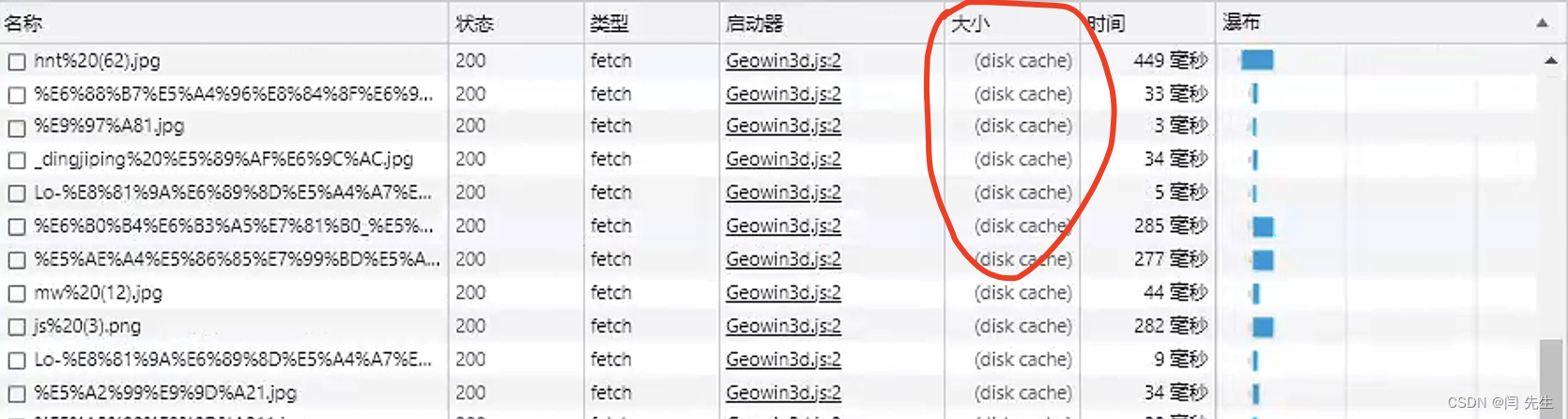
vue离线缓存资源文件
本文章主要是解决大文件,实时请求资源浪费网络资源的问题 从而有效的将解决用户体验的问题 话不多说上才艺 ⬇️⬇️⬇️⬇️⬇️⬇️⬇️ 找到项目中的 index.html 文件,并在 html 标签中加入 manifest"manifest.appcache" 安装 appcache-manifest 包 npm ins…...

2023华为杯研赛数学建模A题B题C题D题E题F题资料 华为杯
本次比赛我们将会全程更新华为杯研赛赛题思路模型及代码,大家查看文末名片获取 之前华为杯相关的资料和助攻可以查看 2022华为杯数学建模研赛选题建议和思路分析_方形件组批优化问题_UST数模社_的博客-CSDN博客 我们华为杯更新的流程如下: A题思路&a…...

星际争霸之小霸王之小蜜蜂(六)--让子弹飞
目录 前言 一、添加子弹设置 二、创建子弹 三、创建绘制和移动子弹函数 四、让子弹飞 五、效果 总结 前言 小蜜蜂的基本操作已经完成了,现在开始编写子弹的代码了。 一、添加子弹设置 在我的预想里,我们的小蜜蜂既然是一只猫,那么放出的子弹…...
opencv简单使用
cv2库安装, conda install opencv-python注意cv2使用时,路径不能有中文。(不然会一直’None’ _ update # 处理中文路径问题 def cv_imread(file_path): #使用之前需要导入numpy、cv2库,file_path为包含中文的路径return cv2.imd…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...
