机器学习十大算法之七——随机森林
0 引言
集成学习(ensemble learning)是时下非常流行的机器学习算法,它本身不是一个单独的机器学习算法,而是通过在数据上构建多个横型,集成所有模型的建模结果,基本上所有的机器学习领域都可以看到集成学习的身影,在现实中集成学习也有相当大的作用,它可以用来做市场营销模拟的建模,统计客户来源,保留和流失,也可用来预测疾病的风险和病患者的易感性。在现在的各种算法竞赛中,随机森林(入门级别容易上手),梯度提升树(GBDT) , Xgboost等集成算法的身影也随处可见,可见其效果之好,应用之广。(一些工业级的算法,比如GBDT、XGBOOST、LGBM都是以决策树为积木搭建出来的)
多个模型集成后的模型叫做集成评估器,集成评估器中的每一个模型叫做基评估器,通常来说有三类集成算法:Bagging、Boosting、Stacking。随机森林是Bagging的代表模型, 他所有的基评估器都是决策树。Bagging法中每一个基评估器是平行的,最后的结果采用平均值或者少数服从多数的原则。集成算法会考虑多个评估器的建模结果,汇总之后得到一个综合结果,以此来获取比单个模型更好的回归或分类表现。
1 随机森林(RF)简介
一棵棵决策树构成了整个随机森林,具体构建树的数量,在scikit-learn中,用“n_estimators”这个参数来控制。在训练某棵树的时候,也不是将样本的所有特征都用来训练,而是会随机选择一部分特征用来训练,目的就是让不同的树重点关注不同的特征。在scikit-learn中,用“max_features”这个参数来控制训练每棵树选取的样本数)。
只要了解决策树的算法,那么随机森林是相当容易理解的。随机森林的算法可以用如下几个步骤概括:
- 用有抽样放回的方法(bootstrap)从样本集中选取n个样本作为一个训练集
- 用抽样得到的样本集生成一棵决策树。在生成的每一个结点:
2.1. 随机不重复地选择d个特征。
2.2 利用这d个特征分别对样本集进行划分,找到最佳的划分特征(可用基尼系数、增益率或者信息增益判别)。 - 重复步骤1到步骤2共k次,k即为随机森林中决策树的个数。
- 用训练得到的随机森林对测试样本进行预测,并用票选法决定预测的结果。
下图比较直观地展示了随机森林算法(图片出自文献2):
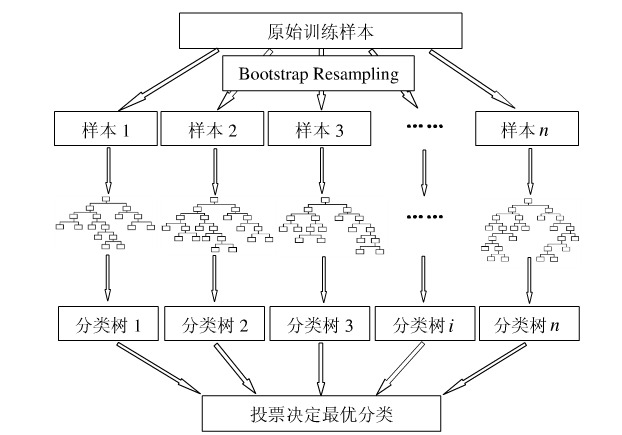
包外估计(Out-of-Bag Estimate)
在随机森林构造过程中进行有放回抽样,一部分样本选不到,这部分样本占整体样本的比重为:
lim N − > ∞ ( 1 − 1 N ) N = 1 e \lim_{N -> \infty}(1-\frac{1}{N})^N=\frac{1}{e} N−>∞lim(1−N1)N=e1
故有36.8%的数据作为包外数据,可用作验证集。包外估计是对集成分类器泛化误差的无偏估计。
3 特征重要性评估
现实情况下,一个数据集中往往有成百上前个特征,如何在其中选择比结果影响最大的那几个特征,以此来缩减建立模型时的特征数是我们比较关心的问题。这样的方法其实很多,比如主成分分析,lasso等等。不过,这里我们要介绍的是用随机森林来对进行特征筛选。
用随机森林进行特征重要性评估的思想其实很简单,说白了就是看看每个特征在随机森林中的每颗树上做了多大的贡献,然后取个平均值,最后比一比特征之间的贡献大小。
3 随机森林优缺点
3.1 优点
- 随机森林机制简单,泛化能力强,可以并行实现(sklearn中
n_jobs控制),因为训练时树与树之间是相互独立的; - 随机森林能处理很高维度的数据(也就是很多特征的数据),并且不用做特征选择。
- 在训练完之后,随机森林能给出哪些特征比较重要。
- 相比单一决策树,能学习到特征之间的相互影响,且不容易过拟合;
- 能直接特征很多的高维数据,因为在训练过程中依旧会从这些特征中随机选取部分特征用来训练;
- 相比SVM,不是很怕特征缺失,因为待选特征也是随机选取;
- 训练完成后可以给出特征重要性。当然,这个优点主要来源于决策树。因为决策树在训练过程中会计算熵或者是基尼系数,越往树的根部,特征越重要。
3.2 缺点
- 随机森林在解决回归问题时,并没有像它在分类中表现的那么好,这是因为它并不能给出一个连续的输出。当进行回归时,随机森林不能够做出超越训练集数据范围的预测,这可能导致在某些特定噪声的数据进行建模时出现过度拟合。(PS:随机森林已经被证明在某些噪音较大的分类或者回归问题上回过拟合)。
- 对于许多统计建模者来说,随机森林给人的感觉就像一个黑盒子,你无法控制模型内部的运行。只能在不同的参数和随机种子之间进行尝试。
- 可能有很多相似的决策树,掩盖了真实的结果。
- 对于小数据或者低维数据(特征较少的数据),可能不能产生很好的分类。(处理高维数据,处理特征遗失数据,处理不平衡数据是随机森林的长处)。
- 执行数据虽然比boosting等快(随机森林属于bagging),但比单只决策树慢多了。
机器学习超详细实践攻略(10):随机森林算法详解及小白都能看懂的调参指南
利用随机森林对特征重要性进行评估
4 Sklearn中随机森林应用
sklearn.ensemble.RandomForestClassifier(n_estimators=10,criterion='gini',max_depth=None,min_samples_split=2,min_samples_leaf=1,min_weight_fraction_leaf=0.0,max_features="auto",max_leaf_nodes=None,min_impurity_decrease=0.0,min_impurity_split=None,bootstrap=True,oob_score=False,n_jobs=1,random_state=None,verbose=0,warm_start=False,class_weight=None
)参数
-
n_estimators:对原始数据集进行有放回抽样生成的子数据集个数,即决策树的个数。若n_estimators太小容易欠拟合,太大不能显著的提升模型,所以n_estimators选择适中的数值,版本0.20的默认值是10,版本0.22的默认值是100。 -
criterion:分裂节点所用的标准,可选“gini”, “entropy”,默认“gini”。 -
max_depth:限制树的最大深度,超过深度的树枝将被全部剪掉。如果为None,则将节点展开,直到所有叶子都是纯净的(只有一个类),或者直到所有叶子都包含少于min_samples_split个样本。默认是None。 -
min_samples_split:拆分内部节点所需的最少样本数:如果为int,则将min_samples_split视为最小值。如果为float,则min_samples_split是一个分数,而ceil(min_samples_split * n_samples)是每个拆分的最小样本数。默认是2。 -
min_samples_leaf:在叶节点处需要的最小样本数。仅在任何深度的分割点在左分支和右分支中的每个分支上至少留下min_samples_leaf个训练样本时,才考虑。这可能具有平滑模型的效果,尤其是在回归中。如果为int,则将min_samples_leaf视为最小值。如果为float,则min_samples_leaf是分数,而ceil(min_samples_leaf * n_samples)是每个节点的最小样本数。默认是1。 -
min_weight_fraction_leaf:在所有叶节点处(所有输入样本)的权重总和中的最小加权分数。如果未提供sample_weight,则样本的权重相等。 -
max_features:寻找最佳分割时要考虑的特征数量:如果为int,则在每个拆分中考虑max_features个特征。如果为float,则max_features是一个分数,并在每次拆分时考虑int(max_features * n_features)个特征。如果为“auto”,则max_features = sqrt(n_features)。如果为“ sqrt”,则max_features = sqrt(n_features)。如果为“ log2”,则max_features = log2(n_features)。如果为None,则max_features = n_features。注意:在找到至少一个有效的节点样本分区之前,分割的搜索不会停止,即使它需要有效检查多个max_features功能也是如此。 -
max_leaf_nodes:最大叶子节点数,整数,默认为None -
min_impurity_decrease:如果分裂指标的减少量大于该值,则进行分裂。 -
min_impurity_split:决策树生长的最小纯净度。默认是0。自版本0.19起不推荐使用:不推荐使用min_impurity_split,而建议使用0.19中的min_impurity_decrease。min_impurity_split的默认值在0.23中已从1e-7更改为0,并将在0.25中删除。 -
bootstrap:是否进行bootstrap操作,bool。默认True。如果bootstrap==True,将每次有放回地随机选取样本,只有在extra-trees中,bootstrap=False -
oob_score:是否使用袋外样本来估计泛化精度。默认False。 -
n_jobs:并行计算数。默认是None。等于-1的时候,表示cpu里的所有core进行工作。 -
random_state:控制bootstrap的随机性以及选择样本的随机性。
verbose:在拟合和预测时控制详细程度。默认是0。 -
class_weight:每个类的权重,可以用字典的形式传入{class_label: weight}。如果选择了“balanced”,则输入的权重为n_samples / (n_classes * np.bincount(y))。 -
ccp_alpha:将选择成本复杂度最大且小于ccp_alpha的子树。默认情况下,不执行修剪。 -
max_samples:如果bootstrap为True,则从X抽取以训练每个基本分类器的样本数。如果为None(默认),则抽取X.shape [0]样本。如果为int,则抽取max_samples样本。如果为float,则抽取max_samples * X.shape [0]个样本。因此,max_samples应该在(0,1)中。是0.22版中的新功能。
面试题
1、为什么要随机抽样训练集?
如果不进行随机抽象,每棵树的训练结果都一样,最终训练出的树的分类结果也是完全一样的
2、为什么要有放回抽样?
每棵树的训练样本都是不同的,不能保证无偏估计。
相关文章:

机器学习十大算法之七——随机森林
0 引言 集成学习(ensemble learning)是时下非常流行的机器学习算法,它本身不是一个单独的机器学习算法,而是通过在数据上构建多个横型,集成所有模型的建模结果,基本上所有的机器学习领域都可以看到集成学习…...
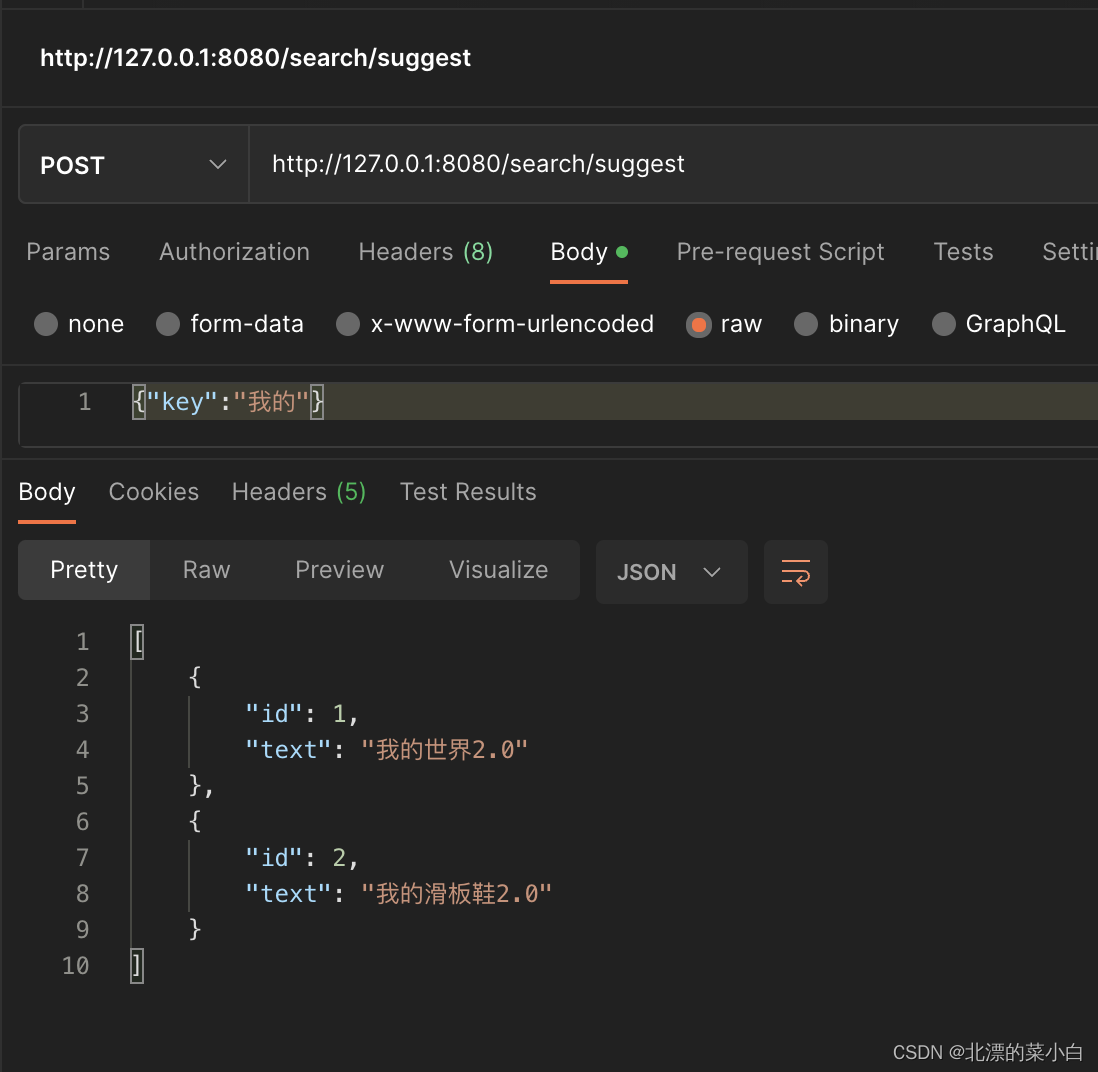
spring boot 3使用 elasticsearch 提供搜索建议
业务场景 用户输入内容,快速返回建议,示例效果如下 技术选型 spring boot 3elasticsearch server 7.17.4spring data elasticsearch 5.0.1elasticsearch-java-api 8.5.3 pom.xml <dependency><groupId>org.springframework.boot</gr…...

住宅IP:解锁更快速、稳定的互联网,你准备好了吗?
随着互联网的广泛普及,我们对网络的需求也越来越高。无论是工作、学习还是娱乐,我们都希望能够享受到更快速、稳定的互联网连接。而在实现这一目标的过程中,住宅IP正逐渐崭露头角,成为了一种备受关注的解决方案。那么,…...

支持dolby vision的盒子接支持dolby vision的电视,在adaptive hdr时,播放非dv的hdr视频,输出sdr
支持dolby vision的盒子接支持dolby vision的电视,setting选择adaptive hdr,按照这个配置在播放非dv的hdr视频时,会输出sdr。 看起来是很不合理的,高级的产品播放高级的片源,却输出低级的画质。 想要搞清楚这个问题&am…...
使用ffmpeg将WebM文件转换为MP4文件的简单应用程序
tiktok网上下载的short视频是webm格式的,有些程序无法处理该程序,比如roop程序,本文介绍了如何使用wxPython库创建一个简单的GUI应用程序,用于将WebM文件转换为MP4文件。这个应用程序使用Python编写,通过调用FFmpeg命令…...

Prompt-“设计提示模板:用更少数据实现预训练模型的卓越表现,助力Few-Shot和Zero-Shot任务”
Prompt任务(Prompt Tasks) 通过设计提示(prompt)模板,实现使用更少量的数据在预训练模型(Pretrained Model)上得到更好的效果,多用于:Few-Shot,Zero-Shot 等…...

玩转Mysql系列 - 第6篇:select查询基础篇
这是Mysql系列第6篇。 环境:mysql5.7.25,cmd命令中进行演示。 DQL(Data QueryLanguage):数据查询语言,通俗点讲就是从数据库获取数据的,按照DQL的语法给数据库发送一条指令,数据库将按需求返回数据。 DQ…...
【SpringCloud技术专题】「Gateway网关系列」(1)微服务网关服务的Gateway组件的原理介绍分析
为什么要有服务网关? 我们都知道在微服务架构中,系统会被拆分为很多个微服务。那么作为客户端要如何去调用这么多的微服务呢?难道要一个个的去调用吗?很显然这是不太实际的,我们需要有一个统一的接口与这些微服务打交道…...

【面试刷题】————STL中的vector是如何实现的?
STL(Standard Template Library)是C标准库中的一部分,它提供了许多常用的数据结构和算法,其中包括了动态数组 vector。 vector std::vector 是一个动态数组,它能够自动调整自己的大小,以适应存储元素的需…...
)
使用钉钉的扫码会出现多个回调(DTFrameLogin)
官方:地址 标题 出现的问题解决后效果正常使用(按照官网的流程进行使用)自己的理解(路人可忽略该内容!) 出现的问题 1692861955468 解决后效果 1692861665687 正常使用(按照官网的流程进行使用) fn.js 该文件就是钉钉官网的js文件,我下载到了…...

Android | 关于 OOM 的那些事儿
作者:345丶 前言 Android 系统对每个app都会有一个最大的内存限制,如果超出这个限制,就会抛出 OOM,也就是Out Of Memory 。本质上是抛出的一个异常,一般是在内存超出限制之后抛出的。最为常见的 OOM 就是内存泄露(大量…...

珠玑妙算游戏
珠玑妙算游戏,OJ练习 一、描述二、方法一三、方法二 一、描述 珠玑妙算游戏(the game of master mind)的玩法如下: 计算机有4个槽,每个槽放一个球,颜色可能是红色(R)、黄色…...

【rust语言】rust多态实现方式
文章目录 前言一、多态二、rust实现多态trait的静态方式还有一种方式可以通过动态分发,还以上面那段代码,比如dyn关键字 泛型方式枚举方式优点:缺点: 总结 前言 学习rust当中遇到了这个问题,记录一下,不对…...

两年半机场,告诉我如何飞翔
为说明如何坐飞机离港,故此记录一篇。何为离港,顾名思义,离开港湾,那何为港湾,便是机场。 机场,一个你可能经常去,亦或不曾去之地。我想,管你去没去过,先说下怎么去&…...
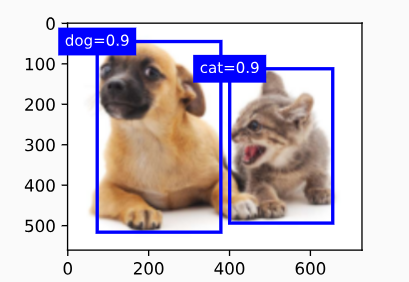
【动手学深度学习】--21.锚框
锚框 学习视频:锚框【动手学深度学习v2】 官方笔记:锚框 1.锚框 目标检测算法通常会在输入图像中采样大量的区域,然后判断这些区域中是否包含我们感兴趣的目标,并调整区域边界从而更准确地预测目标的真实边界框(gro…...
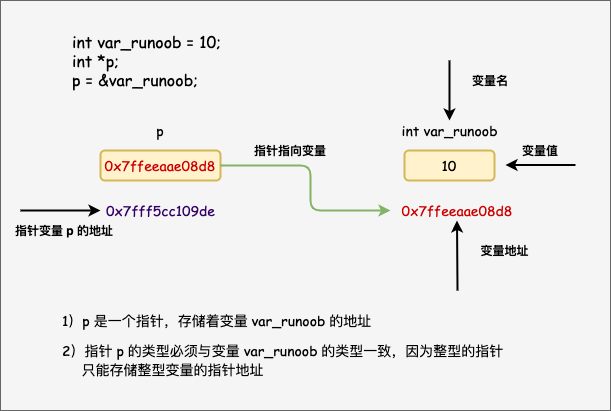
C语言学习笔记(完整版)
文章目录 算法算法的基本概念算法的特征算法的优劣 描述算法三种基本结构流程图N-S流程图伪代码 常量和变量了解数据类型常量整形常量实型常量字符型常量转义字符符号常量 变量整形变量实型变量字符型变量 表达式与运算符赋值运算符和赋值表达式变量赋初值强制类型转换 算术运算…...

【Unity3D赛车游戏】【四】在Unity中添加阿克曼转向,下压力,质心会让汽车更稳定
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:Uni…...

Python爬虫requests判断请求超时并重新post/get发送请求
在使用Python爬虫中,你可以使用requestsimport requests #Python爬虫requests判断请求超时并重新post发送请求,proxies为代理 def send_request_post(url, data, headers , proxies , max_retries3, timeout5):retries 0while retries < max_retries…...

CSS中如何实现多列布局?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 多列布局(Multi-column Layout)⭐ column-count⭐ column-width⭐ column-gap⭐ column-rule⭐ column-span⭐ 示例⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧…...

【C++】string简单实用详解
本片要分享的内容是有关于string的知识,在这之前得介绍一下什么是STL; 目录 1.STL简单介绍 2. string简单介绍 3.string简单使用 3.1.string的定义 3.2.字符串的拼接 3.3.string的遍历 3.3.1.循环遍历 3.3.2.迭代器遍历 4.string的函数构造 1.…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
