05有监督学习——神经网络
-
线性模型
给定n维输入: x = [ x 1 , x 1 , … , x n ] T x = {[{x_1},{x_1}, \ldots ,{x_n}]^T} x=[x1,x1,…,xn]T
线性模型有一个n维权重和一个标量偏差: w = [ w 1 , w 1 , … , w n ] T , b w = {[{w_1},{w_1}, \ldots ,{w_n}]^T},b w=[w1,w1,…,wn]T,b
输出是输入的加权和: y = w 1 x 1 + w 2 x 2 + … + w n x n + b y = {w_1}{x_1} + {w_2}{x_2} + \ldots + {w_n}{x_n} + b y=w1x1+w2x2+…+wnxn+b,向量表示: y = < w , x > + b y = < w,x > + b y=<w,x>+b
1.1 广义线性模型
除了直接让模型预测值逼近实值标记y,我们还可以让它逼近y的衍生物,这就是广义线性模型(generalized linear model)
y = g − 1 ( w T x + b ) y = {g^{ - 1}}({w^T}x + b) y=g−1(wTx+b)
其中 g(.)称为联系函数(link function),要求单调可微。使用广义线性模型我们可以实现强大的非线性函数映射功能。比方说对数线性回归(log-linear regression),令g(.) = In(.),此时模型预测值对应的是真实值标记在指数尺度上的变化。
1.2 Sigmoid函数
σ ( z ) \sigma (z) σ(z) 代表一个常用的逻辑函数(logistic function)为S形函数(Sigmoid function),则:
σ ( z ) = g ( z ) = 1 1 + e − z , z = w T x + b \sigma (z) = g(z) = {1 \over {1 + {e^{ - z}}}},z = {w^T}x + b σ(z)=g(z)=1+e−z1,z=wTx+b
合起来,我们得到的逻辑回归模型的假设函数:
L ( y ^ , y ) = − y log ( y ^ ) − ( 1 − y ) log ( 1 − y ^ ) \mathrm{L}(\hat{y}, y)=-y \log (\hat{y})-(1-y) \log (1-\hat{y}) L(y^,y)=−ylog(y^)−(1−y)log(1−y^) -
分类与回归
-
感知机模型
单层感知机数学模型: y = f ( ∑ i = 1 N w i x i + b ) y = f(\sum\limits_{i = 1}^N {{w_i}{x_i}} + b) y=f(i=1∑Nwixi+b)
其中,f称为激活函数
1986年,Rumelhart和McClIelland为首的科学家提出了BP( Back Propagation )神经网络的概念,是一种按照误差逆向传播算法训练的多层前馈神经网络,目前是应用最广泛的神经网络。
3.1 训练数据
-
收集一些数据点来决定参数值(权重和偏差),例如过去6个月卖的房子。这被称之为训练数据·通常越多越好假设我们有n个样本,记
x = [ x 1 , x 1 , … , x n ] T x = {[{x_1},{x_1}, \ldots ,{x_n}]^T} x=[x1,x1,…,xn]T, y = [ y 1 , y 1 , … , y n ] T y = {[{y_1},{y_1}, \ldots ,{y_n}]^T} y=[y1,y1,…,yn]T3.2衡量预估质量
比较真实值和预估值,例如房屋售价和估价
假设y是真实值, y ^ \hat y y^是估计值,我们可以比较:
ℓ ( y , y ^ ) = 1 2 ( y − y ^ ) 2 \ell(y, \hat{y})=\frac{1}{2}(y-\hat{y})^2 ℓ(y,y^)=21(y−y^)2
这个叫做平方损失
训练损失:
ℓ ( X , y , w , b ) = 1 2 n ∑ i = 1 n ( y i − ⟨ x i , w ⟩ − b ) 2 = 1 2 n ∥ y − X w − b ∥ 2 \ell(\mathbf{X}, \mathbf{y}, \mathbf{w}, b)=\frac{1}{2 n} \sum_{i=1}^n\left(y_i-\left\langle\mathbf{x}_i, \mathbf{w}\right\rangle-b\right)^2=\frac{1}{2 n}\|\mathbf{y}-\mathbf{X} \mathbf{w}-b\|^2 ℓ(X,y,w,b)=2n1i=1∑n(yi−⟨xi,w⟩−b)2=2n1∥y−Xw−b∥2
最小化损失来学习参数:
w ∗ , b ∗ = arg min w , b ℓ ( X , y , w , b ) \mathbf{w}^*, \mathbf{b}^*=\arg \min _{\mathbf{w}, b} \ell(\mathbf{X}, \mathbf{y}, \mathbf{w}, b) w∗,b∗=argw,bminℓ(X,y,w,b)3.3 梯度下降
- 挑选一个初始值 w 0 {w_0} w0
- 重复迭代参数t=1,2,3
w t = w t − 1 − η ∂ ℓ ∂ w t − 1 {w_t} = {w_{t - 1}} - \eta {{\partial \ell } \over {\partial {w_{t - 1}}}} wt=wt−1−η∂wt−1∂ℓ - 沿梯度方向将增加损失函数值
- 学习率:步长的超参数
优点:
1.能够自适应、自主学习。BP可以根据预设参数更新规则,通过不断调整神经网络中的参数,已达到最符合期望的输出。
2.拥有很强的非线性映射能力。
3.误差的反向传播采用的是成熟的链式法则,推导过程严谨且科学。
4.算法泛化能力很强。
缺点:
1.BP神经网络参数众多,每次迭代需要更新较多数量的阈值和权值,故收敛速度比较慢。
2.网络中隐层含有的节点数目没有明确的准则,需要不断设置节点数字试凑,根据网络误差
结果最终确定隐层节点个数
3.BP算法是一种速度较快的梯度下降算法,容易陷入局部极小值的问题。
在深度学习模型中,我们一般习惯在每层神经网络的计算结果送入下一层神经网络之前先经过一个激活函数。
(1)Sigmod函数: f ( x ) = 1 1 + e − x f(x) = {1 \over {1 + {{\rm{e}}^{ - x}}}} f(x)=1+e−x1

(2)Tanh函数: tanh ( x ) = e x − e − x ( e x + e − x ) = 2 ∗ s i g m o d ( 2 x ) − 1 \tanh (x) = {{{e^x} - {e^{ - x}}} \over {({e^x} + {e^{ - x}})}} = 2*sig\bmod (2x) - 1 tanh(x)=(ex+e−x)ex−e−x=2∗sigmod(2x)−1

(3)relu函数: f ( x ) = max ( 0 , x ) f(x) = \max (0,x) f(x)=max(0,x)

神经网络模型可以非常方便地对数据进行升降维,随着特征数量的增多,样本的密度就下降了,继续升维度,就会过拟合,不适用于真实情况
-
欠拟合与过拟合
过拟合和欠拟合可以通过训练误差和泛化误差来定义:
训练误差:模型在训练集上 计算得到的误差泛化误差:模型应用在同样从原始样本的分布中抽取的无限多数据样本时,模型误差的期望。过拟合:模型的训练误差小,泛化误差大欠拟合:模型的训练误差和泛化误差都大过拟合的处理方法:
(1) 正则化:正则化的,但是减少参数的大小,它可以改善或者减少过拟合问题
(2) 数据增强: 数据的质量、数量和难度等进行增强
(3)降维: 即丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征,也可以使用一些模型选择的算法来帮忙。
(4)集成学习方法: 集成学习是把多个模型集成在一起,来降低单一模型的过拟合风险。过拟合的处理方法:
(1)添加新特征
(2)增加模型复杂度
(3)减小正则化系数 -
正则
深度学习中的正则可以看作通过约束模型复杂度来防止过拟合现象的一些手段。首先,模型复杂度是由模型的参数量大小和参数的可取值范围一起决定的。因此正则方法也大致分为两个方向:
一个方向致力于约束模型参数量,例如Dropout;
一个方向致力于约束模型参数的取值范围,例如weight decay。
权重衰减方法:
(1)使用均方范数作为硬性限制
通过限制参数值的选择范围来控制模型容量:
min ℓ ( w , b ) \min \ell (w,b) minℓ(w,b)subject to ∥ w ∥ 2 ≤ θ {\left\| {\rm{w}} \right\|^2} \le \theta ∥w∥2≤θ
通常不限制b
(2)使用均方范数作为柔性限制
对于每个 θ \theta θ,都可以找到 λ \lambda λ,使得之前的目标函数等价于下面式子:
min ℓ ( w , b ) + λ 2 ∥ w ∥ 2 \min \ell (w,b) + {\lambda \over 2}{\left\| w \right\|^2} minℓ(w,b)+2λ∥w∥2
超参数 λ \lambda λ控制了正则项的重要程度:
- λ \lambda λ = 0 无作用
- λ → ∞ , w ∗ → 0 \lambda \to \infty ,w* \to 0 λ→∞,w∗→0
-
数据增强
-
数值稳定性
这种数值不稳定性问题再深度学习训练过程中被称作梯度消失和梯度爆炸。
梯度消失:由于累乘导致的梯度接近0的现象,此时训练没有进展。
梯度爆炸:由于累乘导致计算结果超出数据类型能记录的数据范围,导致报错。防止出现数值不稳定原因的方法是进行数据归一化处理。
数据归一化处理:
(1)归一化(最大-最小规范化)——将数据映射到【0,1】区间
x ∗ = x − x min x max − x min x* = {{x - {x_{\min }}} \over {{x_{\max }} - {x_{\min }}}} x∗=xmax−xminx−xmin
数据归一化的目的是使得各特征对目标变量的影响一致,会将特征数据进行伸缩变化,所以数据归一化是会改变特征数据分布的。
(2)Z-Score标准化——处理后的数据均 值为0,方差为1
x ∗ = x − μ σ x* = {{x - \mu } \over \sigma } x∗=σx−μ
数据标准化为了不同特征之间具备可比性,经过标准化变换之后的特征数据分布没有发生改变。
就是当数据特征取值范围或单位差异较大时,最好是做一下标准化处理。
相关文章:

05有监督学习——神经网络
线性模型 给定n维输入: x [ x 1 , x 1 , … , x n ] T x {[{x_1},{x_1}, \ldots ,{x_n}]^T} x[x1,x1,…,xn]T 线性模型有一个n维权重和一个标量偏差: w [ w 1 , w 1 , … , w n ] T , b w {[{w_1},{w_1}, \ldots ,{w_n}]^T},b w[w1,w1,…,wn]T,b 输…...
JavaWeb_LeadNews_Day7-ElasticSearch, Mongodb
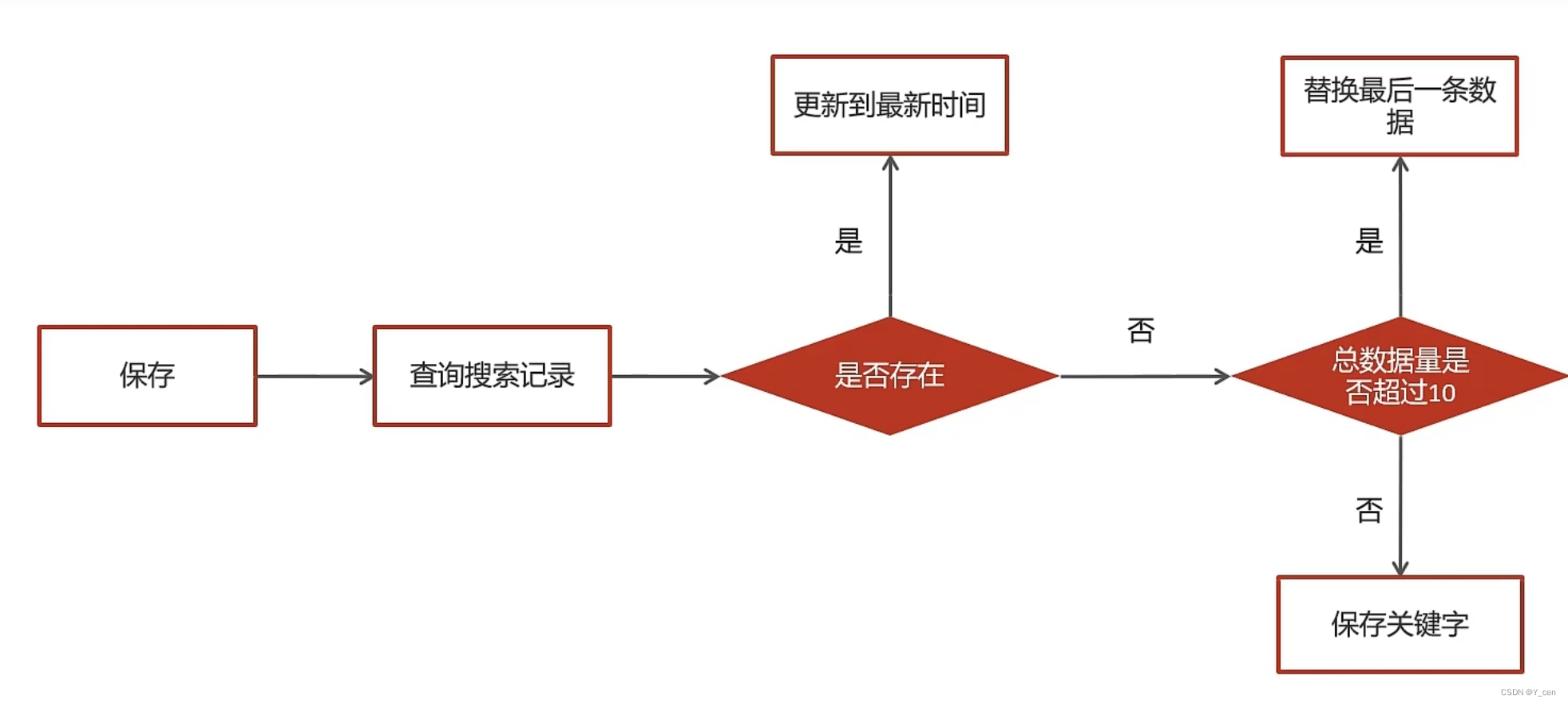
JavaWeb_LeadNews_Day7-ElasticSearch, Mongodb elasticsearch安装配置 app文章搜索创建索引库app文章搜索思路分析具体实现 新增文章创建索引思路分析具体实现 MongoDB安装配置SpringBoot集成MongoDB app文章搜索记录保存搜索记录思路分析具体实现 查询搜索历史删除搜索历史 搜…...

redux中间件理解,常见的中间件,实现原理。
文章目录 一、Redux中间件介绍1、什么是Redux中间件2、使用redux中间件 一、Redux中间件介绍 1、什么是Redux中间件 redux 提供了类似后端 Express 的中间件概念,本质的目的是提供第三方插件的模式,自定义拦截 action -> reducer 的过程。变为 actio…...
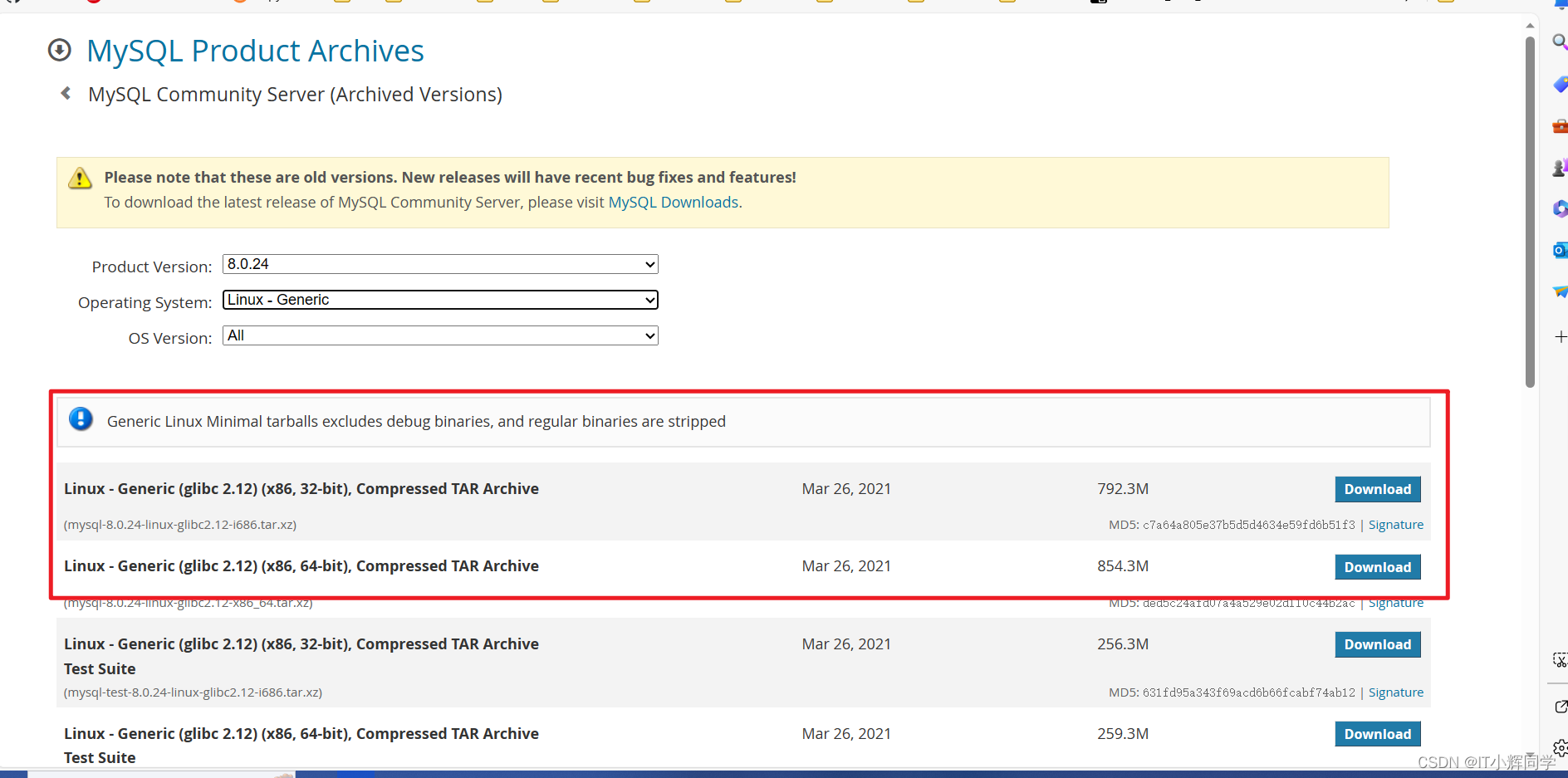
麒麟系统上安装 MySQL 8.0.24
我介绍一下在麒麟系统上安装 MySQL 8.0.24 的详细步骤,前提是您已经下载了 mysql-8.0.24-linux-glibc2.12-x86_64.tar.xz 安装包。其实安装很简单,但是有坑,而且问题非常严重!由于麒麟系统相关文章博客较少,导致遇到了…...
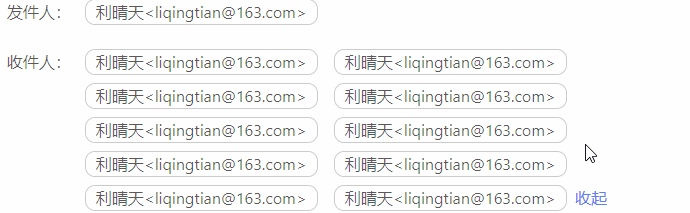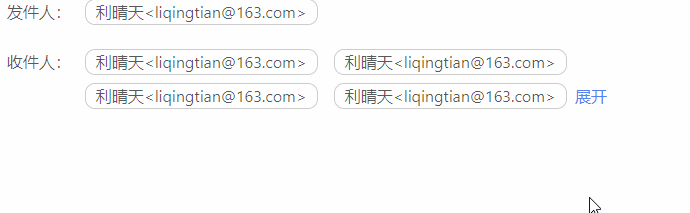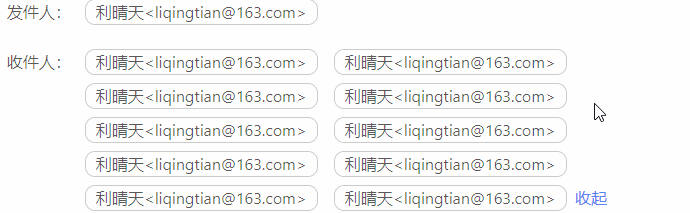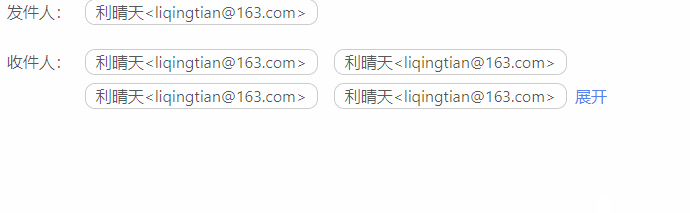
vue 展开和收起
效果图 代码块 <div><span v-for"(item,index) in showHandleList" :key"item.index"><span>{{item.emailFrom}}</span></span><span v-if"this.list.length > 4" click"showAll !showAll">{…...
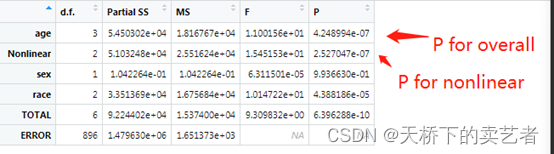
限制立方样条(RCS)中的P for overall和P for nonlinear的计算
最近不少人私信我,说有些SCI文章报了两个P值一个是P for overall,一个是P for nonlinear,就像下图这样,问我P for overall怎么计算。 P for overall我也不清楚是什么,有些博主说这个是总效应的P值,但是我没有找到相关出处。但是怎…...

vue3+ts引入echarts并实现自动缩放
第一种写法(不支持随页面大小变化而缩放) 统一的HTML页面 <div class"content_box" ref"barChart" id"content_box"></div>TS语法 <script setup lang"ts">import * as echarts from echar…...
Compressor For Mac强大视频编辑工具 v4.6.5中文版
Compressor for Mac是苹果公司推出的一款视频压缩工具,可以将高清视频、4K视频、甚至是8K视频压缩成适合网络传输或存储的小文件。Compressor支持多种视频格式,包括H.264、HEVC、ProRes和AVC-Intra等,用户可以根据需要选择不同的压缩格式。 …...

maven工程的目录结构
https://maven.apache.org/guides/introduction/introduction-to-the-standard-directory-layout.html maven工程的目录结构: 在maven工程的根目录下面,是pom.xml文件。此外,还有README.txt、LICENSE.txt等文本文件,便于用户能够…...

5.1 webrtc线程模型
那从今天开始呢?我们来了解一下y8 tc线程相关的内容,那在开始之前呢?我们先来看一下,我们本章都要讲解哪些知识? 那第一个呢?是线程的基础知识,这块内容呢?主要是为大家做一下回顾&a…...

【Linux网络】Cookie和session的关系
目录 一、Cookie 和 session 共同之处 二、Cookie 和 session 区别 2.1、cookie 2.2、session 三、cookie的工作原理 四、session的工作原理 一、Cookie 和 session 共同之处 Cookie 和 Session 都是用来跟踪浏览器用户身份的会话方式。 二、Cookie 和 session 区别 2.…...

android 硬编码保存mp4
目录 java imagereader编码保存 java NV21toYUV420SemiPlanar 编码保存视频用: imageReader获取nv21 代码来自博客: 【Android Camera2】彻底弄清图像数据YUV420_888转NV21问题/良心教学/避坑必读!_yuv420888转nv21_奔跑的鲁班七号的博客-CSDN博客 …...

gitlab合并分支
我的分支为 cheng 第一步: 增加新的代码 第二步:提交并推送 第三步:打开gitlab,找到对应项目 这样就成功把cheng分支合并到dev-test分支了...
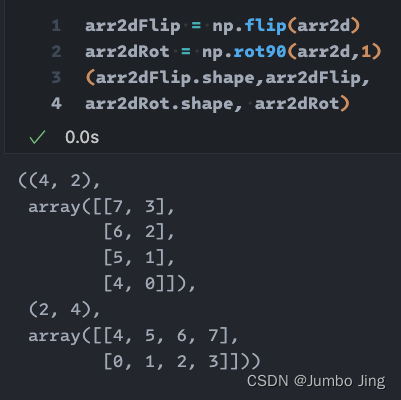
手撕 `np.transpose` : 三维数组的循环转置
手撕 np.transpose : 三维数组的循环转置 手撕 np.transpose 2D 何为transpose ? 如上图: 二维的例子, 直观地理解就是沿着对角线拉平(对角关系左上右下依旧), 其他位置依次填充. 2. 2D数组中0,1 为原始参, 1,0 为转置参 - 原始参即数组的原始形态: 比如👆&#x…...
计算机竞赛 基于Django与深度学习的股票预测系统
文章目录 0 前言1 课题背景2 实现效果3 Django框架4 数据整理5 模型准备和训练6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 **基于Django与深度学习的股票预测系统 ** 该项目较为新颖,适合作为竞赛课题方向ÿ…...

CSS 小技能(一):HTML 两个图片竖着平铺、设置图片点击、设置滚动条颜色
下面的代码没有考虑响应式的效果,如果考虑的话还需要一些代码进行处理。 【注】当时写的时候仅考虑了 webkit 内核的浏览器,如果是 IE 或者其他浏览器,请增加额外的 CSS 样式进行控制。 <!DOCTYPE html> <html> <head>&l…...
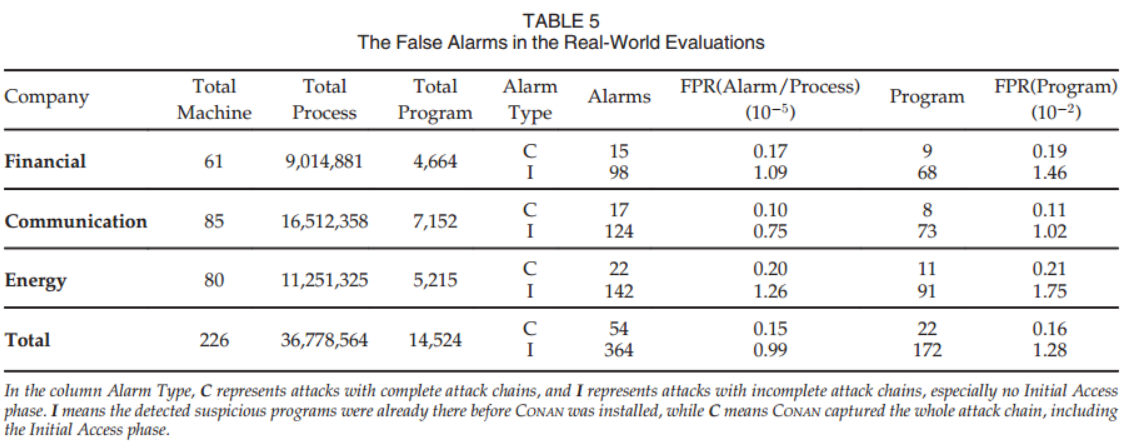
【论文阅读】CONAN:一种实用的、高精度、高效的APT实时检测系统(TDSC-2020)
CONAN:A Practical Real-Time APT Detection System With High Accuracy and Efficiency TDSC-2020 浙江大学 Xiong C, Zhu T, Dong W, et al. CONAN: A practical real-time APT detection system with high accuracy and efficiency[J]. IEEE Transactions on Dep…...
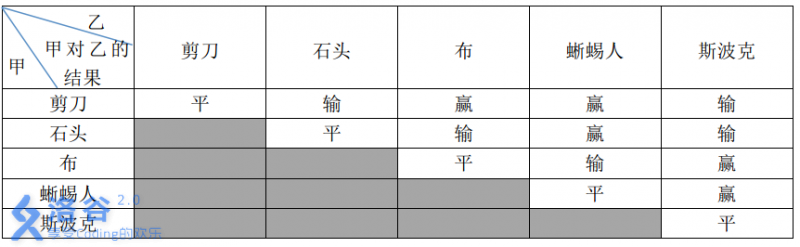
P1328 [NOIP2014 提高组] 生活大爆炸版石头剪刀布
题目描述 石头剪刀布是常见的猜拳游戏:石头胜剪刀,剪刀胜布,布胜石头。如果两个人出拳一样,则不分胜负。在《生活大爆炸》第二季第 8 集中出现了一种石头剪刀布的升级版游戏。 升级版游戏在传统的石头剪刀布游戏的基础上,增加了两个新手势: 斯波克:《星际迷航》主…...
基于Android水果蔬菜果蔬到家商城系统 微信小程序uniAPP的开发与实现
果蔬到家是商家针对用户必不可少的一个部分。在商铺发展的整个过程中,果蔬到家担负着最重要的角色。为满足如今日益复杂的管理需求,各类果蔬到家程序也在不断改进。本课题所设计的springboot基于HBuilder X的果蔬到家APP,使用SpringBoot框架&…...
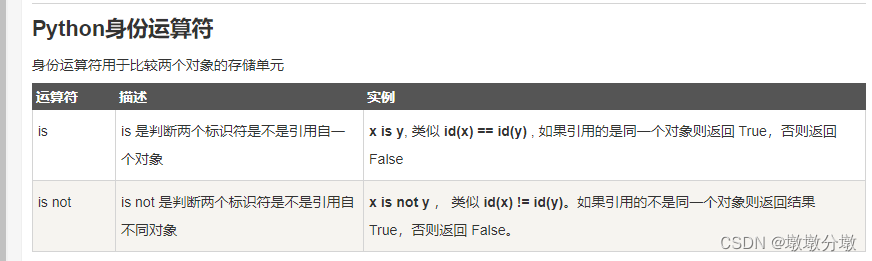
【Python】从入门到上头—Python基础(2)
文章目录 一.基础语法1.编码2.标识符3.保留字4.注释5.行与缩进6.多行语句7.数字(Number)类型8.字符串(String)9.空行10.等待用户输入11.同一行显示多条语句12.多个语句构成代码组13.print 输出14.import 与 from...import 二.基本数据类型1.变量和赋值2.多个变量赋值3.标准数据…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...
