CSDN编程题-每日一练(2023-08-25)
CSDN编程题-每日一练(2023-08-25)
- 一、题目名称:影分身
- 二、题目名称:小鱼的航程(改进版)
- 三、题目名称:排查网络故障
一、题目名称:影分身
时间限制:1000ms内存限制:256M
题目描述:
已知字符串str。字符串str包含字符’x’,’y’。 如果相邻的两个字符不同,消除两个字符,优先从左边进行消除。 xyyx - > yx ->
输入描述:
输入多个字符。(1<=len<=1e5)
输出描述:
输出最后的分身
🚩 示例:
✔️ 示例1:
输入
xyyyy
输出
yyy
🔔 解题思路:
根据题目描述,我们需要对输入的字符串进行处理,消除相邻的不同字符。优先从左边开始消除。可以使用栈(Stack)数据结构来实现。
代码1如下:
s = input().strip() # 输入字符串##函数 calc 接受一个字符串参数 s,返回一个字符串作为最后的分身
def calc(s: str) -> str:stack = [] # 初始化一个空栈 stack,用于存储字符for ch in s: # 遍历输入的字符串s,依次处理每个字符if not stack or ch == stack[-1]: # 栈为空(not stack)或者当前字符 ch 与栈顶字符相同 (ch == stack[-1])##将当前字符 ch 入栈 (stack.append(ch))stack.append(ch)else: ## 如果栈不为空,并且当前字符 ch 与栈顶字符不同,说明找到了一对相邻不同的字符,将栈顶字符出栈 (stack.pop())stack.pop()##遍历完整个字符串后,栈中剩余的字符即为最后的分身
##使用 join 函数将栈中的字符按照出栈顺序组合起来,返回结果return ''.join(stack) result = calc(s) # 消除相邻的不同字符
print(result) # 输出最后的分身
代码2如下:
#include <iostream>
#include <stack>
#include <string>##定义一个名为 calc的函数,接受一个常量引用字符串作为参数,并返回一个字符串。
std::string calc(const std::string& s) {std::stack<char> stack; #声明一个字符栈 stack,用于模拟栈结构#使用 for 循环遍历输入字符串 s,依次处理每个字符for (char ch : s) {##对于每个字符 ch 进行判断:
##1、如果栈为空(stack.empty())或者当前字符 ch 与栈顶字符相同(ch == stack.top()),将当前字符 ch 入栈(stack.push(ch))。
##2、如果栈不为空,并且当前字符 ch 与栈顶字符不同,说明找到了一对相邻不同的字符,将栈顶元素出栈(stack.pop())if (stack.empty() || ch == stack.top()) {stack.push(ch);} else {stack.pop();}}##使用 for 循环遍历输入字符串 s 中的每个字符 ch。对于每个字符,如果栈为空或者当前字符与栈顶字符相同,将当前字符入栈;否则,说明找到了一对相邻不同的字符,将栈顶元素出栈std::string result; #创建一个空字符串 result,用于保存最后的分身while (!stack.empty()) { ##使用 while 循环将栈中的字符依次出栈,并将出栈的字符加到 result 的前面result = stack.top() + result;stack.pop();}##最后返回保存最后的分身的字符串 resultreturn result;
}int main() {##声明一个字符串 s,用于存储输入的字符串std::string s;##使用 std::getline 函数从标准输入中获取一行字符串std::getline(std::cin, s);##调用 calc函数处理输入字符串,得到最后的分身,将其赋给字符串变量 resultstd::string result = calc(s);##使用 std::cout 将结果输出到标准输出流,并在末尾添加换行符std::cout << result << std::endl;##程序正常结束return 0;
}
二、题目名称:小鱼的航程(改进版)
时间限制:1000ms内存限制:256M
题目描述:
有一只小鱼,它上午游泳150公里,下午游泳100公里,晚上和周末都休息(实行双休日),假设从周x(1<=x<=7)开始算起,请问这样过了n天以后,小鱼一共累计游泳了多少公里呢?
输入描述:
输入两个整数x,n(表示从周x算起,经过n天,n在long int范围内)。
输出描述:
输出一个整数,表示小鱼累计游泳了多少公里。
🚩示例:
✔️示例1
输入
3 10
输出
2000
🔔 解题思路:
根据输入的起始天数x和总天数n,计算一定天数内(包括起始天数)游泳的总公里数。
代码1如下:
# 读取输入,起始天数x和经过的天数n
x, n = map(int, input().split())def solution(x, n):#计算出从起始天数开始经过n天后的总天数total_days :total_days = n + x - 1total_days = n + x - 1#计算完整周期(一周)的游泳公里数total_kmtotal_km = total_days // 7 * 250 * 5##计算额外的天数excess_days ,即不足一周的天数excess_days = total_days % 7##循环遍历range(excess_days)来判断每一天是否是工作日(小于5),如果是则将游泳公里数增加250米for i in range(excess_days):if i < 5:total_km += 250
##循环遍历从周一到前一天(range(1, x))的天数,在工作日(小于6)中减去250米的游泳公里数for i in range(1, x):if i < 6:total_km -= 250###计算得到的游泳公里数total_km作为函数的返回值return total_km###调用solution(x, n)
total_km=solution(x, n)
print(total_km)
代码2如下:
#include <stdio.h>
#include <stdlib.h>#define MAX_SIZE 100## 注意:n在long int范围内
long int solution(long int x, long int n) {long int total_days = n + x - 1;long int total_km = total_days / 7 * 250 * 5;long int excess_days = total_days % 7;for (long int i = 0; i < excess_days; i++) {if (i < 5) {total_km += 250;}}for (long int i = 1; i < x; i++) {if (i < 6) {total_km -= 250;}}return total_km;
}int main() {long int x, n;scanf("%ld %ld", &x, &n);long int total_km = solution(x, n);printf("%ld\n", total_km);return 0;
}
三、题目名称:排查网络故障
时间限制:1000ms内存限制:256M
题目描述:
A地跟B地的网络中间有n个节点(不包括A地和B地),相邻的两个节点是通过网线连接。正常的情况下,A地和B地是可以连通的,有一天,A地和B地突然不连通了,已知只有一段网线出问题(两个相邻的节点)小明需要排查哪段网线出问题。他的排查步骤是: 1。 选择某个中间节点 2。 在这个节点上判断跟A地B地是否连通,用来判断那一边出问题 请问小明最少要排查多少次,才能保证一定可以找到故障网线。
输入描述:
一个正整数 n (n <= 10^18),表示A地和B地之间的节点数。
输出描述:
输出一个数字,代表保证一定可以找到故障网线的前提下,小明最少要排查多少次?
🚩示例:
✔️示例1
输入
2
输出
2
🔔 解题思路:
假设节点数为n,我们可以将整个网络划分为两半,即左边的节点和右边的节点。如果某个节点被选为判断节点,那么它所在的位置就决定了是哪一半出了问题。
对于一个给定的节点数n,首先找到最接近n的2的幂次方m,使得m <= n。然后,排查的次数就是最接近n的2的幂次方的对数log2(m)。
首先观察题目中的连接方式,可以发现节点数n与排查次数node_number之间存在一定的关系。
1、假设排查次数为x,那么排查的节点个数应为2^x - 1。
2、当排查的节点个数超过了n时,即2^x - 1 > n,说明排查次数为x-1时已经可以确定故障网线的位置。
3、根据以上思路,可以用循环不断将n除以2,直到n小于等于0为止,每次循环时check_number 加1。
4、最后输出check_number 即为所求的最少排查次数。
代码1如下:*
##A地和B地之间的节点数n
n = int(input())
##计数器check_number , 排查次数
check_number = 0
##当n大于0时,执行循环体
while n > 0:
##将n除以2,结果赋值给n,相当于将节点数减半,直到n小于等于0为止n = n // 2
###每次循环时,将check_number 加1check_number += 1
###输出check_number即为所求的最少排查次数
print(check_number)
代码2如下:*
🔔 解题思路:
首先,我们需要找到一个节点,通过判断这个节点是否与A地和B地连通,来确定故障网线是在节点的哪一边。
假设A地和B地之间有n个节点,我们可以将节点数n表示成二进制形式。例如,n=2时,二进制为10,表示有两个节点。
我们观察一下,当节点数为2的幂次方时,排查次数最少。例如,n=2时,只有节点2需要排查;n=4时,只有节点4需要排查;n=8时,只有节点8需要排查,以此类推。
因此,我们可以先找到节点数n的二进制表示中最高位的1的位置,记为highest_bit_pos。然后,我们构造一个掩码mask,将最高位1右边的所有位都置为1。再将节点数n与掩码mask进行或运算,得到masked_n。
最后,我们统计masked_n中1的个数,即为小明最少要排查的次数。
n = int(input())# 1、找到最高位1的位置,即二进制字符串的长度减去3,
### 如: bin(2)的结果是字符串'0b10'。长度为4,这表示二进制数2的二进制表示形式为10。前缀0b表示这是一个二进制数,最高位为1
highest_bit_pos = len(bin(n)) - 3# 2、将最高位1右边的所有位都置为1
##使用左移运算符<<将1左移highest_bit_pos个位数,然后减去1,生成一个二进制数,其中最高位1的右边都是1,其余位为0。这个二进制数被赋值给变量mask
mask = (1 << highest_bit_pos) - 1##3、按位或运算符|将n与mask进行按位或操作
###将masked_n的最高位1右边的所有位都置为1,而其余位与n保持相同
masked_n = n | mask# 4、计算1的个数
##将masked_n转换为二进制字符串,然后使用count()函数计算其中字符'1'的个数
count = bin(masked_n).count('1')#5、输出count,即masked_n中1的个数
print(count)🔔 示例输入解释:
例如,当输入为2时,输出为2。解释:
1、节点数n为2,二进制表示为10。
2、找到最高位1的位置为1,即highest_bit_pos=1。
3、构造掩码mask,将最高位1右边的所有位都置为1,即mask=1。
4、将节点数n与掩码mask进行或运算,得到masked_n=3。
5、统计masked_n中1的个数,即为小明最少要排查的次数,即count=2。
相关文章:

CSDN编程题-每日一练(2023-08-25)
CSDN编程题-每日一练(2023-08-25) 一、题目名称:影分身二、题目名称:小鱼的航程(改进版)三、题目名称:排查网络故障 一、题目名称:影分身 时间限制:1000ms内存限制:256M 题目描述&am…...

前端面试:【前端工程化】构建工具Webpack、Parcel和Rollup
嗨,亲爱的前端开发者!在现代Web开发中,前端工程化变得愈发重要。构建工具如Webpack、Parcel和Rollup帮助我们自动化任务、管理依赖、优化性能等。本文将深入探讨这三个前端构建工具,帮助你了解它们的优点和用途。 1. Webpack&…...

大型企业是否有必要进行数字化转型?
在数字化、信息化、智能化蓬勃发展的今天,初创公司可以很轻易的布局规划数字化发展的路径。而对于大型企业而言,其已经形成了较为成熟稳固的业务及组织架构,是否还有必要根据自身行业发展特点寻求数字化转型?(比如制造…...

05有监督学习——神经网络
线性模型 给定n维输入: x [ x 1 , x 1 , … , x n ] T x {[{x_1},{x_1}, \ldots ,{x_n}]^T} x[x1,x1,…,xn]T 线性模型有一个n维权重和一个标量偏差: w [ w 1 , w 1 , … , w n ] T , b w {[{w_1},{w_1}, \ldots ,{w_n}]^T},b w[w1,w1,…,wn]T,b 输…...
JavaWeb_LeadNews_Day7-ElasticSearch, Mongodb
JavaWeb_LeadNews_Day7-ElasticSearch, Mongodb elasticsearch安装配置 app文章搜索创建索引库app文章搜索思路分析具体实现 新增文章创建索引思路分析具体实现 MongoDB安装配置SpringBoot集成MongoDB app文章搜索记录保存搜索记录思路分析具体实现 查询搜索历史删除搜索历史 搜…...

redux中间件理解,常见的中间件,实现原理。
文章目录 一、Redux中间件介绍1、什么是Redux中间件2、使用redux中间件 一、Redux中间件介绍 1、什么是Redux中间件 redux 提供了类似后端 Express 的中间件概念,本质的目的是提供第三方插件的模式,自定义拦截 action -> reducer 的过程。变为 actio…...
麒麟系统上安装 MySQL 8.0.24
我介绍一下在麒麟系统上安装 MySQL 8.0.24 的详细步骤,前提是您已经下载了 mysql-8.0.24-linux-glibc2.12-x86_64.tar.xz 安装包。其实安装很简单,但是有坑,而且问题非常严重!由于麒麟系统相关文章博客较少,导致遇到了…...
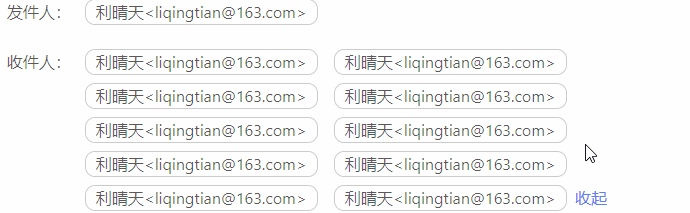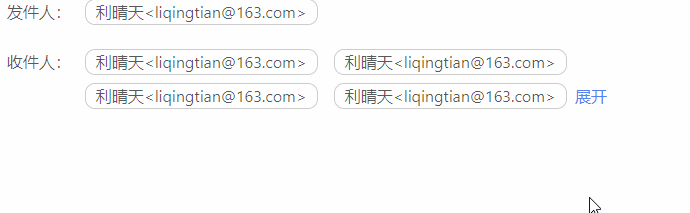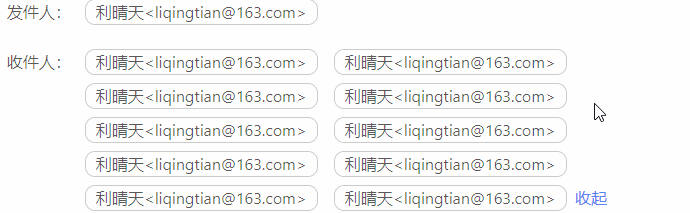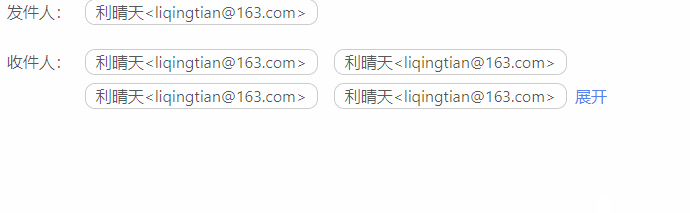
vue 展开和收起
效果图 代码块 <div><span v-for"(item,index) in showHandleList" :key"item.index"><span>{{item.emailFrom}}</span></span><span v-if"this.list.length > 4" click"showAll !showAll">{…...
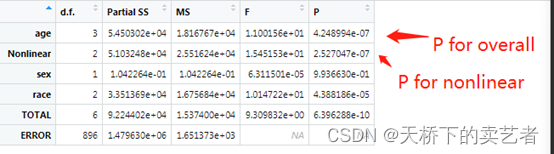
限制立方样条(RCS)中的P for overall和P for nonlinear的计算
最近不少人私信我,说有些SCI文章报了两个P值一个是P for overall,一个是P for nonlinear,就像下图这样,问我P for overall怎么计算。 P for overall我也不清楚是什么,有些博主说这个是总效应的P值,但是我没有找到相关出处。但是怎…...

vue3+ts引入echarts并实现自动缩放
第一种写法(不支持随页面大小变化而缩放) 统一的HTML页面 <div class"content_box" ref"barChart" id"content_box"></div>TS语法 <script setup lang"ts">import * as echarts from echar…...
Compressor For Mac强大视频编辑工具 v4.6.5中文版
Compressor for Mac是苹果公司推出的一款视频压缩工具,可以将高清视频、4K视频、甚至是8K视频压缩成适合网络传输或存储的小文件。Compressor支持多种视频格式,包括H.264、HEVC、ProRes和AVC-Intra等,用户可以根据需要选择不同的压缩格式。 …...

maven工程的目录结构
https://maven.apache.org/guides/introduction/introduction-to-the-standard-directory-layout.html maven工程的目录结构: 在maven工程的根目录下面,是pom.xml文件。此外,还有README.txt、LICENSE.txt等文本文件,便于用户能够…...

5.1 webrtc线程模型
那从今天开始呢?我们来了解一下y8 tc线程相关的内容,那在开始之前呢?我们先来看一下,我们本章都要讲解哪些知识? 那第一个呢?是线程的基础知识,这块内容呢?主要是为大家做一下回顾&a…...

【Linux网络】Cookie和session的关系
目录 一、Cookie 和 session 共同之处 二、Cookie 和 session 区别 2.1、cookie 2.2、session 三、cookie的工作原理 四、session的工作原理 一、Cookie 和 session 共同之处 Cookie 和 Session 都是用来跟踪浏览器用户身份的会话方式。 二、Cookie 和 session 区别 2.…...

android 硬编码保存mp4
目录 java imagereader编码保存 java NV21toYUV420SemiPlanar 编码保存视频用: imageReader获取nv21 代码来自博客: 【Android Camera2】彻底弄清图像数据YUV420_888转NV21问题/良心教学/避坑必读!_yuv420888转nv21_奔跑的鲁班七号的博客-CSDN博客 …...

gitlab合并分支
我的分支为 cheng 第一步: 增加新的代码 第二步:提交并推送 第三步:打开gitlab,找到对应项目 这样就成功把cheng分支合并到dev-test分支了...
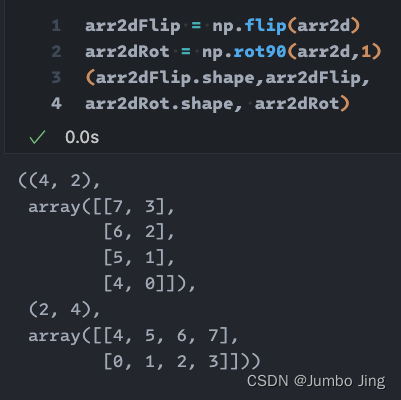
手撕 `np.transpose` : 三维数组的循环转置
手撕 np.transpose : 三维数组的循环转置 手撕 np.transpose 2D 何为transpose ? 如上图: 二维的例子, 直观地理解就是沿着对角线拉平(对角关系左上右下依旧), 其他位置依次填充. 2. 2D数组中0,1 为原始参, 1,0 为转置参 - 原始参即数组的原始形态: 比如👆&#x…...
计算机竞赛 基于Django与深度学习的股票预测系统
文章目录 0 前言1 课题背景2 实现效果3 Django框架4 数据整理5 模型准备和训练6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 **基于Django与深度学习的股票预测系统 ** 该项目较为新颖,适合作为竞赛课题方向ÿ…...

CSS 小技能(一):HTML 两个图片竖着平铺、设置图片点击、设置滚动条颜色
下面的代码没有考虑响应式的效果,如果考虑的话还需要一些代码进行处理。 【注】当时写的时候仅考虑了 webkit 内核的浏览器,如果是 IE 或者其他浏览器,请增加额外的 CSS 样式进行控制。 <!DOCTYPE html> <html> <head>&l…...
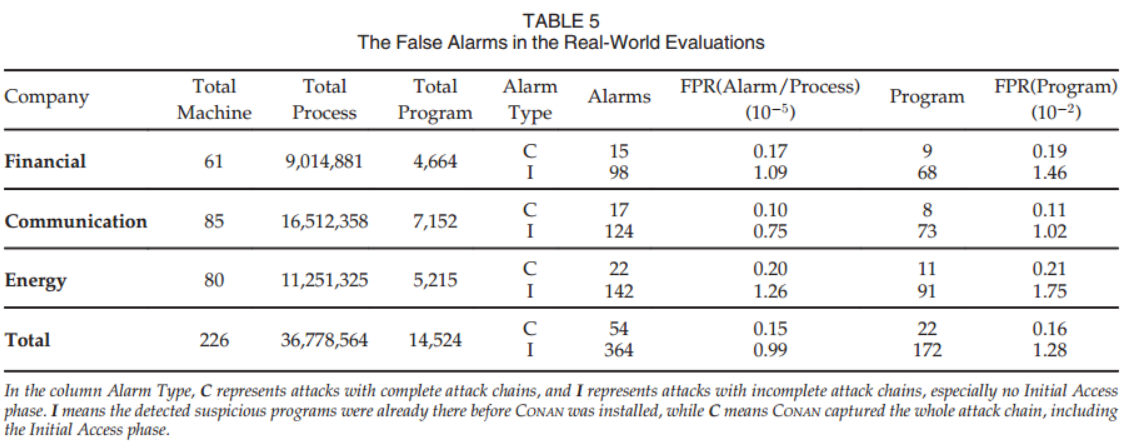
【论文阅读】CONAN:一种实用的、高精度、高效的APT实时检测系统(TDSC-2020)
CONAN:A Practical Real-Time APT Detection System With High Accuracy and Efficiency TDSC-2020 浙江大学 Xiong C, Zhu T, Dong W, et al. CONAN: A practical real-time APT detection system with high accuracy and efficiency[J]. IEEE Transactions on Dep…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...
