每日两题 111二叉树的最小深度 112路径总和(递归)
111
题目
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例 1:
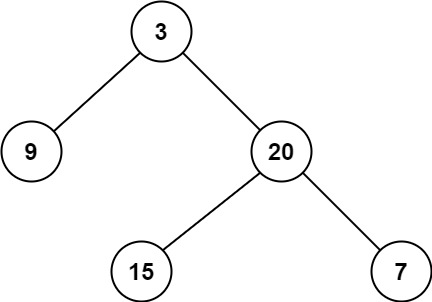
输入:root = [3,9,20,null,null,15,7] 输出:2
示例 2:
输入:root = [2,null,3,null,4,null,5,null,6] 输出:5
题解
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int minDepth(TreeNode root) {if (root == null) {return 0;}if (root.left == null && root.right == null) {return 1;}int ans = Integer.MAX_VALUE;if (root.left != null) {ans = Math.min(minDepth(root.left),ans);}if (root.right != null) {ans = Math.min(minDepth(root.right),ans);}return ans + 1;}
}112
题目
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
示例 1:

输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22 输出:true 解释:等于目标和的根节点到叶节点路径如上图所示。
示例 2:
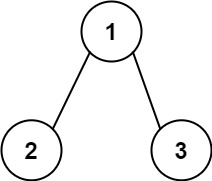
输入:root = [1,2,3], targetSum = 5 输出:false 解释:树中存在两条根节点到叶子节点的路径: (1 --> 2): 和为 3 (1 --> 3): 和为 4 不存在 sum = 5 的根节点到叶子节点的路径。
示例 3:
输入:root = [], targetSum = 0 输出:false 解释:由于树是空的,所以不存在根节点到叶子节点的路径。
题解
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean hasPathSum(TreeNode root, int targetSum) {if (root == null) {return false;}if (root.left == null && root.right == null) {return targetSum == root.val;} return hasPathSum(root.left,targetSum - root.val) || hasPathSum(root.right,targetSum - root.val);}
}相关文章:

每日两题 111二叉树的最小深度 112路径总和(递归)
111 题目 给定一个二叉树,找出其最小深度。 最小深度是从根节点到最近叶子节点的最短路径上的节点数量。 说明:叶子节点是指没有子节点的节点。 示例 1: 输入:root [3,9,20,null,null,15,7] 输出:2示例 2&#x…...
实训笔记8.24
实训笔记8.24 8.24笔记一、Sqoop数据迁移工具1.1 Sqoop的基本概念1.2 Sqoop的基本操作1.2.1 命令语法1.2.2 list-databases1.2.3 list-tables1.2.3 eval1.2.4 import1.2.5 export1.2.6 导入 二、Flume日志采集工具2.1 数据采集的问题2.2 数据采集一般使用的技术2.3 扩展&#x…...
Linux下的系统编程——系统调用(五)
前言: 由操作系统实现并提供给外部应用程序的编程接口。(Application Programming Interface,API)。系统调用就是应用程序同系统之间数据交互的桥梁。 open/close函数 1.open函数: (1)int open(char *pathname, int flags) …...

动物体外受精手术VR模拟仿真培训系统保证学生及标本的安全
奶牛是养殖业主要的资源,因此保证奶牛的健康对养殖业的成功和可持续发展具有重要已用,奶牛有一些常见易发病,一旦处理不当,对奶牛业都会造成较大的经济损失,传统的奶牛手术培训实操难度大、风险高且花费大,…...
微信小程序|步骤条
步骤条是现代用户界面设计中常见的元素之一,它能够引导用户按照预定顺序完成一系列任务或步骤。在小程序中,实现步骤条可以为用户提供更好的导航和引导,使用户体验更加流畅和直观。本文将介绍如何在小程序中实现步骤条,并逐步展示实现的过程和关键技巧 目录 步骤条的作用及…...

如何才能设计出“好的”测试用例?
软件测试用例的设计质量直接影响到测试的完整性、有效性以及自动化测试的实施效果,是软件测试成功的重要保证,良好的软件测试用例对于提高测试的有效性和效率至关重要。那大家知道好的测试用例该怎么写吗?应该从哪几个方面来撰写呢࿱…...
DirectExchange直连交换机
目录 一、简介 二、使用步骤 三、demo 父pom文件 pom文件 配置文件 config 消费者 生产者 测试 一、简介 直连型交换机,根据消息携带的路由键将消息投递给对应队列。 大致流程,有一个队列绑定到一个直连交换机上,同时赋予一个路由…...

Shell 编程:探索 Shell 的基本概念与用法
目录 Shell 简介 Shell 脚本 Shell 脚本运行 Shell 变量 1、创建变量和赋值 2、引用变量 3、修改变量的值 4、只读变量 5、删除变量 6、环境变量 Shell 字符串操作 1、拼接字符串 2、字符串长度 3、字符串截取 Shell 数组 1、创建数组 2、访问数组元素 shell …...
【Git分支操作---讲解二】
Git分支操作---讲解二 查看分支创建分支切换分支修改分支切换分支合并分支合并分支【冲突】(只会修改主分支不会修改其他分支)什么时候会有冲突? 查看分支 创建分支 切换分支 修改分支 切换分支 合并分支 合并分支【冲突】(只会修改主分支不会修改其他分支) 什么时…...

vue2+qrcodejs2+clipboard——实现二维码展示+下载+复制到剪切板——基础积累
最近在写后台管理系统时,遇到一个需求就是要实现二维码的展示下载复制到剪切板。 效果图如下: 1.二维码展示下载功能——qrcodejs20.0.2 我是安装的qrcodejs20.0.2,指定了具体的版本号,也可以安装默认的当前稳定版本࿰…...

【PHP】echo 输出数组报Array to string conversion解决办法
代码: <?PHP echo "Hello World!";$demoName array("kexuexiong","xiong");echo "<pre>";var_dump($demoName);echo $demoName; print_r($demoName);echo "</pre>"; ?>输出结果࿱…...
)
Arduino驱动MiCS-4514气体传感器(气体传感器篇)
目录 1、传感器特性 2、控制器和传感器连线图 3、驱动程序...

marked在vue项目中改变超链接跳转方式和图片放大预览
marked在vue项目中改变超链接跳转方式和图片放大预览 这里我是另起一个js文件对marked的配置做了修改,参考如下 import marked from marked let renderer new marked.Renderer() const linkRenderer renderer.link const imgRenderer renderer.image // 超链接…...
leetcode485. 最大连续 1 的个数
思路:【双指针】 left左边界,right往右跑遇到0,则计算该长度。并更新cnt(最大连续1个数)。 class Solution { public:int findMaxConsecutiveOnes(vector<int>& nums) {int left 0, right 0;int cnt 0;…...

linux 源代码编译
源代码编译 有时候会在linux上下载源码包,然后进行编译成可执行的文件,这个过程需要经过configure、make、make install、make clean四个步骤 configure 为这个程序在当前的操作系统环境下选择合适的编译器和环境参数来编译该代码 make 对程序代码进行编…...

C语言日常刷题 1
文章目录 题目答案与解析1234.5.6. 题目 1、执行下面程序,正确的输出是( ) int x5,y7; void swap() { int z; zx; xy; yz; } int main() { int x3,y8; swap(); printf(“%d,%d\n”,x, y); return 0; } A: 5,7 B: 7,5 C: 3,8 D: 8…...
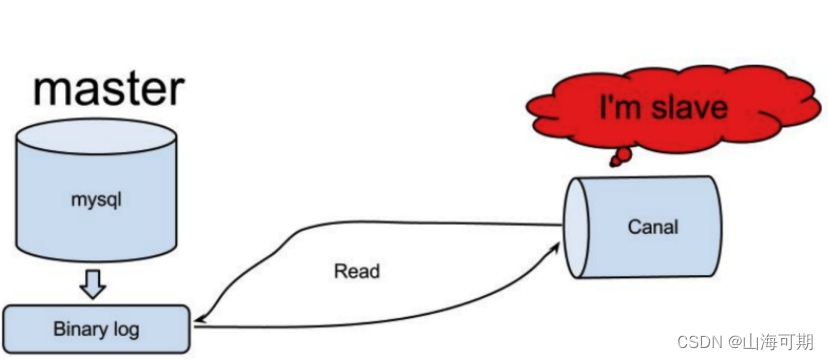
es和数据库同步方案
5.5 课程信息索引同步 5.5.1 技术方案 通过向索引中添加课程信息最终实现了课程的搜索,我们发现课程信息是先保存在关系数据库中,而后再写入索引,这个过程是将关系数据中的数据同步到elasticsearch索引中的过程,可以简单成为索引…...

手机NFC功能是什么?
手机NFC功能是什么? 随着智能手机的不断发展和普及,NFC(近场通讯)功能已经成为了我们生活中不可或缺的一部分。NFC是一种无线通信技术,可以让手机和其他设备之间进行快速的数据交换和支付操作。那么,手机NFC功能是什么࿱…...
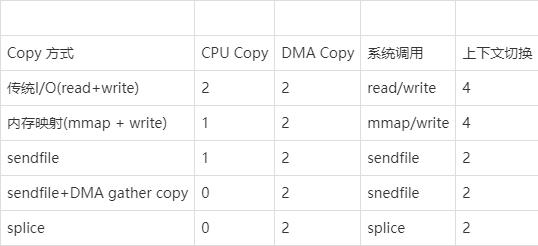
零拷贝技术详解
当涉及到网络编程和IO操作时,数据拷贝是一个常见的性能瓶颈。传统的数据拷贝过程中,数据需要从内核缓冲区复制到用户空间缓冲区,然后再从用户空间缓冲区复制到内核缓冲区,这个过程会耗费大量的CPU时间和内存带宽,降低系…...

【VS Code插件开发】消息通信(四)
🐱 个人主页:不叫猫先生,公众号:前端舵手 🙋♂️ 作者简介:前端领域优质作者、阿里云专家博主,共同学习共同进步,一起加油呀! 📢 资料领取:前端…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
