数据结构--算法的时间复杂度和空间复杂度
文章目录
- 算法效率
- 时间复杂度
- 时间复杂度的概念
- 大O的渐进表示法
- 计算实例
- 时间复杂度
- 实例
- 常见复杂度对比
- 例题
算法效率
算法效率是指算法在计算机上运行时所消耗的时间和资源。这是衡量算法执行速度和资源利用情况的重要指标。
例子:
long long Fib(int N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}
这是一个斐波那契函数,用的是递归的计算方法,每次创建函数就会在栈区开辟一块空间,递归次数越多,开辟空间越多;
所以,代码的简洁说明不了算法的效率;
算法效率的评估主要包括时间复杂度和空间复杂度:
-
时间复杂度:时间复杂度描述了算法执行所需的时间随输入规模增加而增长的趋势。常见的时间复杂度包括常数时间O(1)、线性时间O(n)、对数时间O(log n)、平方时间O(n²)等。通过分析算法中关键操作的执行次数来确定时间复杂度,通常使用大O符号表示。
-
空间复杂度:空间复杂度描述了算法在执行过程中所需的额外存储空间随输入规模增加而增长的趋势。常见的空间复杂度包括常数空间O(1)、线性空间O(n)、对数空间O(log n)等。通过分析算法中使用的数据结构和辅助空间来确定空间复杂度。
评估算法效率时,我们希望选择具有更低时间复杂度和空间复杂度的算法,以提高程序的执行速度和资源利用率。但需要注意的是,时间复杂度和空间复杂度通常存在着一定的取舍关系,有时需要在时间和空间之间做出权衡。
除了时间复杂度和空间复杂度,还可以考虑一些实际情况下的算法效率问题,如最坏情况、平均情况和最好情况下的执行时间,以及算法在特定硬件环境下的性能等。综合考虑这些因素可以更全面地评估算法的效率。
为了提高算法效率,我们可以采用一些常见的优化方法,如减少循环次数、使用合适的数据结构和算法、剪枝和缓存等。同时,也可以借助工具和框架来提升算法效率,如并行计算、GPU加速、分布式计算等。
时间复杂度
时间复杂度的概念
在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
例子:计算Func1中的++count语句执行了多少次?
void Func1(int N)
{int count = 0;for (int i = 0; i < N ; ++ i){for (int j = 0; j < N ; ++ j){++count;}}for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
两个循环嵌套就是N^2,再一个单独的循环2*N,加上10;
那么
F(N)=N^2+2*N+10;
N=10时,F(N)=130
N=100时,F(N)=10210
N=1000时,F(N)=1002010
会发现N越大,F(N)越接近N^2;
在实际计算时间复杂度中,我们其实不一定要精准的计算出执行的次数,只需要大概的执行次数,那么这里我们使用大O的渐进表示法;
大O的渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。是一种用于衡量算法时间复杂度的渐进表示方法;
推导大O阶方法:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
用大O的渐进表示法,Func1的时间复杂度为:O(N^2)
N=10时,F(N)=100
N=100时,F(N)=10000
N=1000时,F(N)=1000000
通过计算我们发现,这样的表示方法去掉那些对结果影响不大的项,简明了洁表示出执行次数;
对于一些算法,会有好坏的情况,对于这种情况我们取最坏的情况;
例如:在一个长度为N数组中搜索一个数据x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
时间复杂度O(N);
计算实例
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
在这里M是一个常数项,N是一个未知数,所以我们可以先把常数项略去;然后就只剩下2N,通过计算规则,省去最高项的常数;那么这个函数的时间复杂度为O(N);
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++ k){++count;}for (int k = 0; k < N ; ++ k){++count;}printf("%d\n", count);
}
在这里,M与N都是未知数,且它们是同阶的,所以对于这种情况就要分类讨论:
M与N差不多大,那么时间复杂度:O(M)或O(N)
M远大于N,时间复杂度:O(M)
N远大于M,时间复杂度:O(N)
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++ k){++count;}printf("%d\n", count);
}
这里给出了明确的次数,所以时间复杂度为O(1);
const char * strchr ( const char * str, int character );
查找字符串中第一个出现的字符返回指向 C 字符串
str 中第一个出现的字符的指针。
终止空字符被视为 C 字符串的一部分。因此,也可以定位它以检索指向字符串末尾的指针。
这个就是在字符串中寻找一个字符,对于这种就要分好坏情况;
最好1次,最坏N次,时间复杂度一般看最坏,时间复杂度为 O(N)。
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
这是一个冒泡排序,很明显这个两个循环在嵌套;外循环执行1次,内循环就得执行N次;那么外循环执行N次,总共就执行N^2次
时间复杂度O(N^2);
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n-1;// [begin, end]:begin和end是左闭右闭区间,因此有=号while (begin <= end){int mid = begin + ((end-begin)>>1);if (a[mid] < x)begin = mid+1;else if (a[mid] > x)end = mid-1;elsereturn mid;}return -1;
}
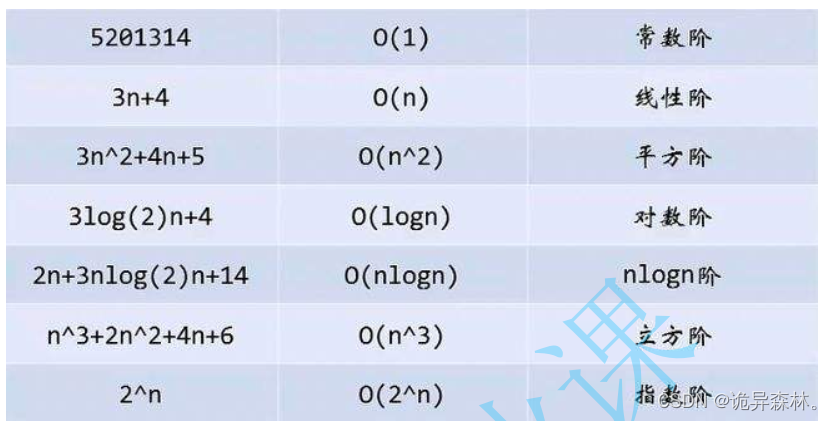
这是一个二分查找函数,也叫折半查找;我们以最坏的情况去看,每循环一次这个数组的长度就会减半,假设以N表示数组的长度,我们要在数组中寻找一个数,那么假设寻找了x次,那么通过计算2^x=N;再通过换算就是x=log2 N;2是对数的底数,由于底数不好表示,所以对于这个函数的时间复杂度就是为O(logN);
long long Fac(size_t N)
{
if(0 == N)
return 1;
return Fac(N-1)*N;
}
这是一个阶乘递归函数,每递归一次N减1,直至为0,才返回;
那么时间复杂度为O(N)
long long Fib(size_t N)
{
if(N < 3)
return 1;
return Fib(N-1) + Fib(N-2);
}
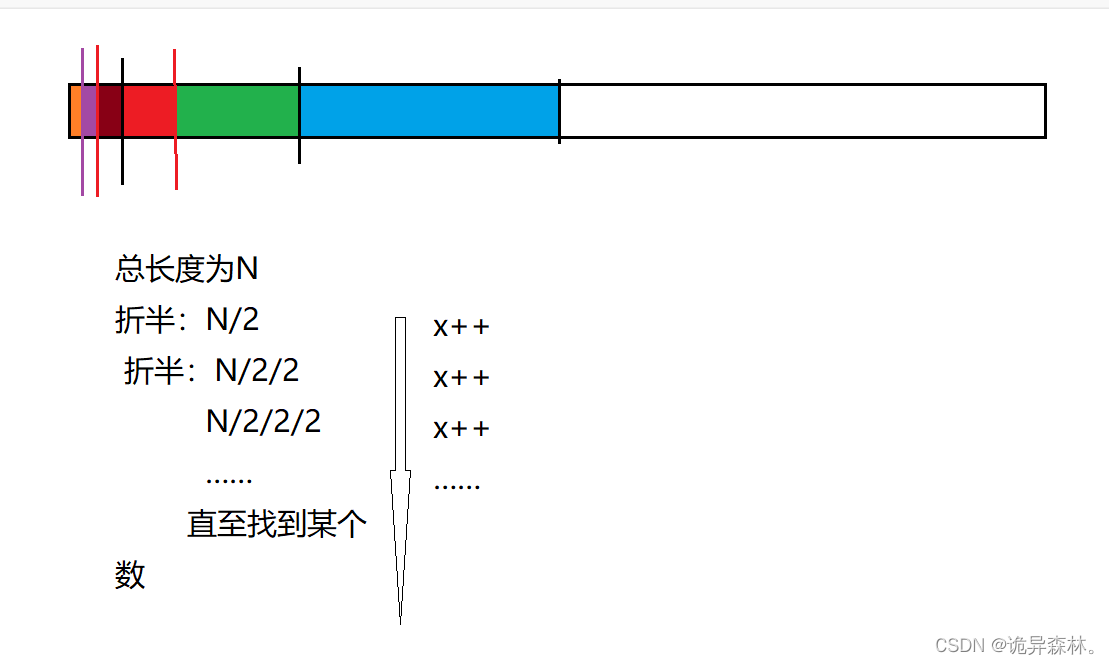
这是开头的例子,斐波那契递归函数,每次在函数中就会递归到两个函数中去;
递归到最后,会发现像个金字塔一样,全部加起来F(N)=1+2+4+8+……+2(N-1),由数学的等比求和公式得F(N)=2^N-1;
那么时间复杂度为F(N)=2^N;
时间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
实例
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
在这里函数所开辟的空间都是局部变量在栈区开辟的,是已经确定下来的;
所以,空间复杂度为O(1)
long long* Fibonacci(size_t n)
{if(n==0)return NULL;long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; ++i){fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray;
}
这里用了malloc函数在堆区开辟了N个额外空间,所以
空间复杂度为O(N)
long long Fac(size_t N)
{if(N == 0)return 1;return Fac(N-1)*N;
}
这里用了递归的方法,每递归一次就会在栈帧中开辟一次空间,总共开辟N次,每次空间内为常数次大,所以
空间复杂度O(N);
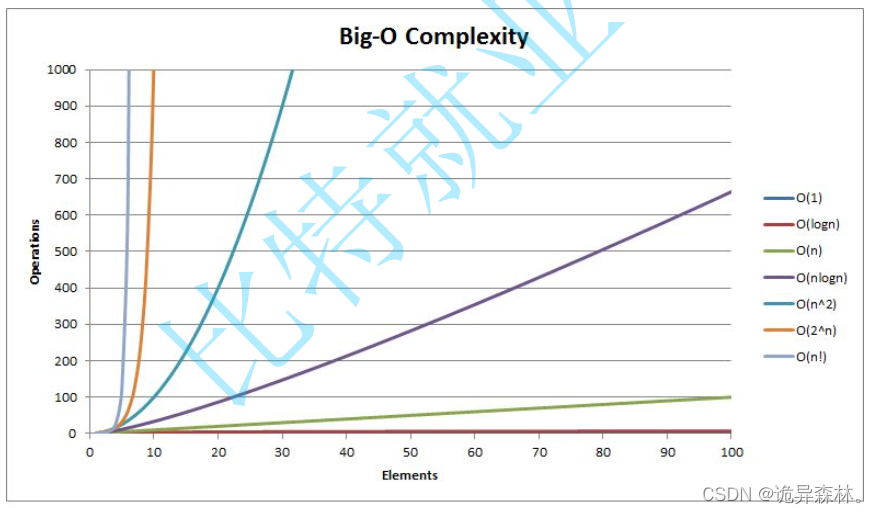
常见复杂度对比
例题
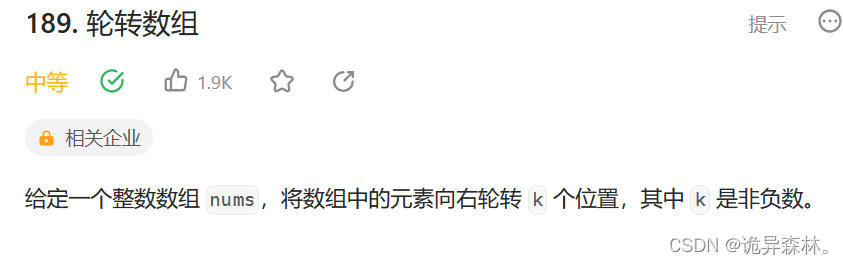

这里用三种办法来解答:
第一种:

时间复杂度:O(N^2)
空间复杂度:O(1)
这里利用这种方法,就是用两个循环嵌套,最终就得出了复杂度;
第二种:

通过开辟额外空间,将对应位置的数字进行放入新数组中,最后再返回到原数组中;
时间复杂度:O(N)
空间复杂度:O(N)
void rotate(int* nums, int numsSize, int k){//开辟额外空间int* new=(int*)malloc(sizeof(int)*numsSize);//当k长度超过数组长度时k%=numsSize;memcpy(new,nums+numsSize-k,sizeof(int)*k);memcpy(new,nums,sizeof(int)*(numsSize-k));memcpy(nums,new,sizeof(int)*numsSize);free(new);}
第三种:

利用倒置再倒置的方法就将数组右旋;
时间复杂度:O(N)
空间复杂度:O(1)
//将数组进行倒置
void reserve(int* sem,int left,int right)
{while(left<right){int tmp=sem[left];sem[left]=sem[right];sem[right]=tmp;left++;right--;}}
void rotate(int* nums, int numsSize, int k){k%=numsSize;//如果k的长度大于numsize,需要取余//利用部分数组倒置,在全数组倒置的方法进行轮转reserve(nums,0,numsSize-k-1);reserve(nums,numsSize-k,numsSize-1);reserve(nums,0,numsSize-1);}相关文章:

数据结构--算法的时间复杂度和空间复杂度
文章目录 算法效率时间复杂度时间复杂度的概念大O的渐进表示法计算实例 时间复杂度实例 常见复杂度对比例题 算法效率 算法效率是指算法在计算机上运行时所消耗的时间和资源。这是衡量算法执行速度和资源利用情况的重要指标。 例子: long long Fib(int N) {if(N …...
Vue中使用element-plus中的el-dialog定义弹窗-内部样式修改-v-model实现-demo
效果图 实现代码 <template><el-dialog class"no-code-dialog" v-model"isShow" title"没有收到验证码?"><div class"nocode-body"><div class"tips">请尝试一下操作</div><d…...
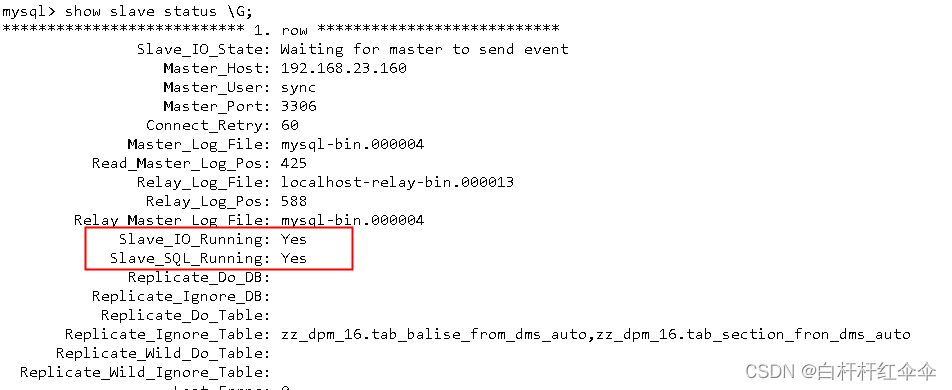
MySQL 主从配置
环境 centos6.7 虚拟机两台 主:192.168.23.160 从:192.168.23.163 准备 在两台机器上分别安装mysql5.6.23,安装完成后利用临时密码登录mysql数据修改root的密码;将my.cnf配置文件放至/etc/my.cnf,重启mysql服务进…...

上海亚商投顾:创业板指反弹大涨1.26% 核污染概念股午后全线走强
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。 市场情绪 三大指数今日集体反弹,沪指午后冲高回落,创业板指盘中涨超2%,尾盘涨幅也有所收…...

Mysql数据库管理
一、数据库基本概念 数据 使用一些介质进行存储,例如文字存在文档中 数据库可以完成数据持久化保存快速提取 那么想要实现以上功能,需要编写一系列的规则--》SQL语句 SQL语句 按功能分类: 增删改查 数据库类型:关系型数据库、非关系型数据库…...
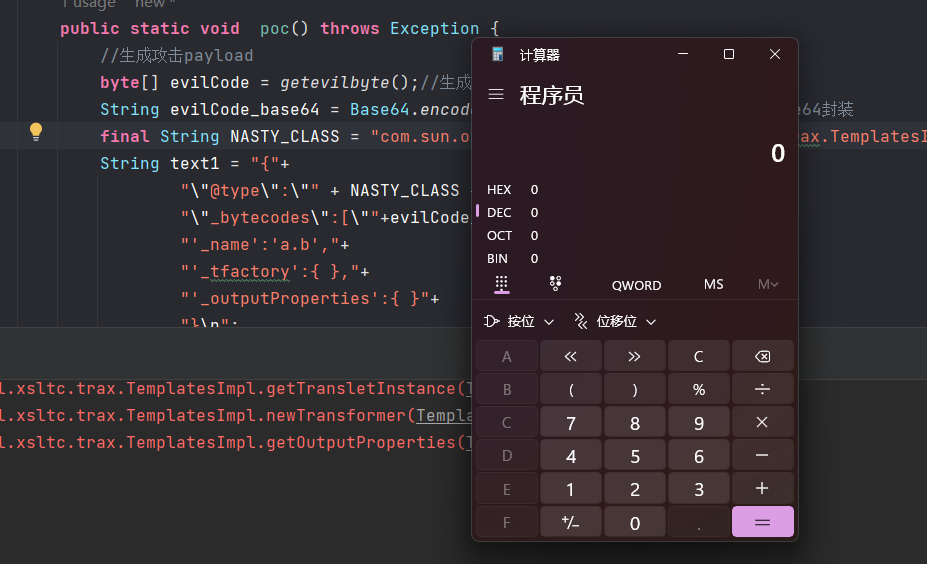
【java安全】FastJson反序列化漏洞浅析
文章目录 【java安全】FastJson反序列化漏洞浅析0x00.前言0x01.FastJson概述0x02.FastJson使用序列化与反序列化 0x03.反序列化漏洞0x04.漏洞触发条件0x05.漏洞攻击方式JdbcRowSetImpl利用链TemplatesImpl利用链**漏洞版本**POC漏洞分析 【java安全】FastJson反序列化漏洞浅析 …...
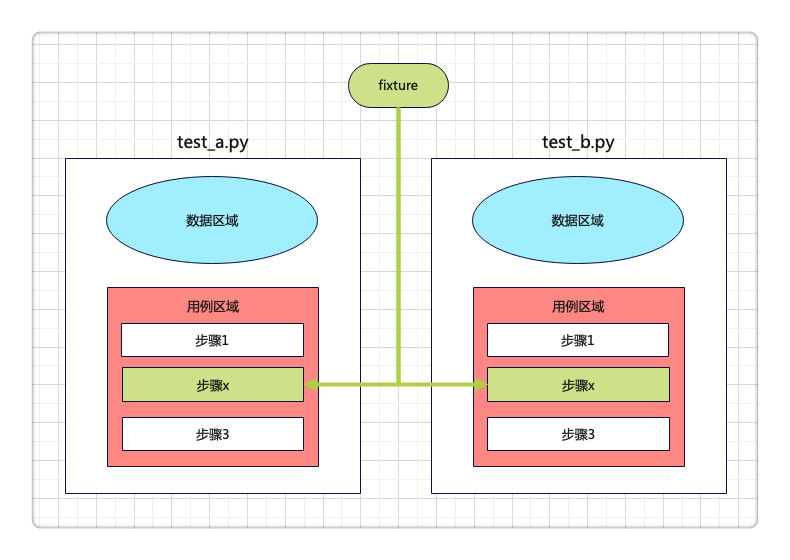
pytestx重新定义接口框架设计
概览 脚手架: 目录: 用例代码: """ 测试登录到下单流程,需要先启动后端服务 """test_data {"查询SKU": {"skuName": "电子书"},"添加购物车": {"sk…...

【文生图系列】Stable Diffusion原理篇
文章目录 Stable Diffusion的组成什么是扩散扩散是如何工作的去噪声绘制图像将文本信息添加到图像生成器中参考 “文生图”,或者AI绘画,最近异常火爆,输入一些描述性的语句,AI就能够生成相应的画作。甚至引发了一个问题࿱…...
ARM-汇编指令
一,map.lds文件 链接脚本文件 作用:给编译器进行使用,告诉编译器各个段,如何进行分布 /*输出格式:32位可执行程序,小端对齐*/ OUTPUT_FORMAT("elf32-littlearm", "elf32-littlearm",…...

Java相关知识对应leetcode
力扣账号:华为邮箱 类知识点力扣链接Integer转为String Character 判断字符是否是字母或者数字转为小写字母 不可修改 String 转为字符串数组 是否包含某个字符或者字符位置 可修改 StringBuffer 单个字符获取 string转为StringBufferStringBuffer转为String字符…...

js中?.、??、??=的用法及使用场景
上面这个错误,相信前端开发工程师应该经常遇到吧,要么是自己考虑不全造成的,要么是后端开发人员丢失数据或者传输错误数据类型造成的。因此对数据访问时的非空判断就变成了一件很繁琐且重要的事情,下面就介绍ES6一些新的语法来方便…...

每日一题:leetcode 1109 航班预订统计
这里有 n 个航班,它们分别从 1 到 n 进行编号。 有一份航班预订表 bookings ,表中第 i 条预订记录 bookings[i] [firsti, lasti, seatsi] 意味着在从 firsti 到 lasti (包含 firsti 和 lasti )的 每个航班 上预订了 seatsi 个座…...
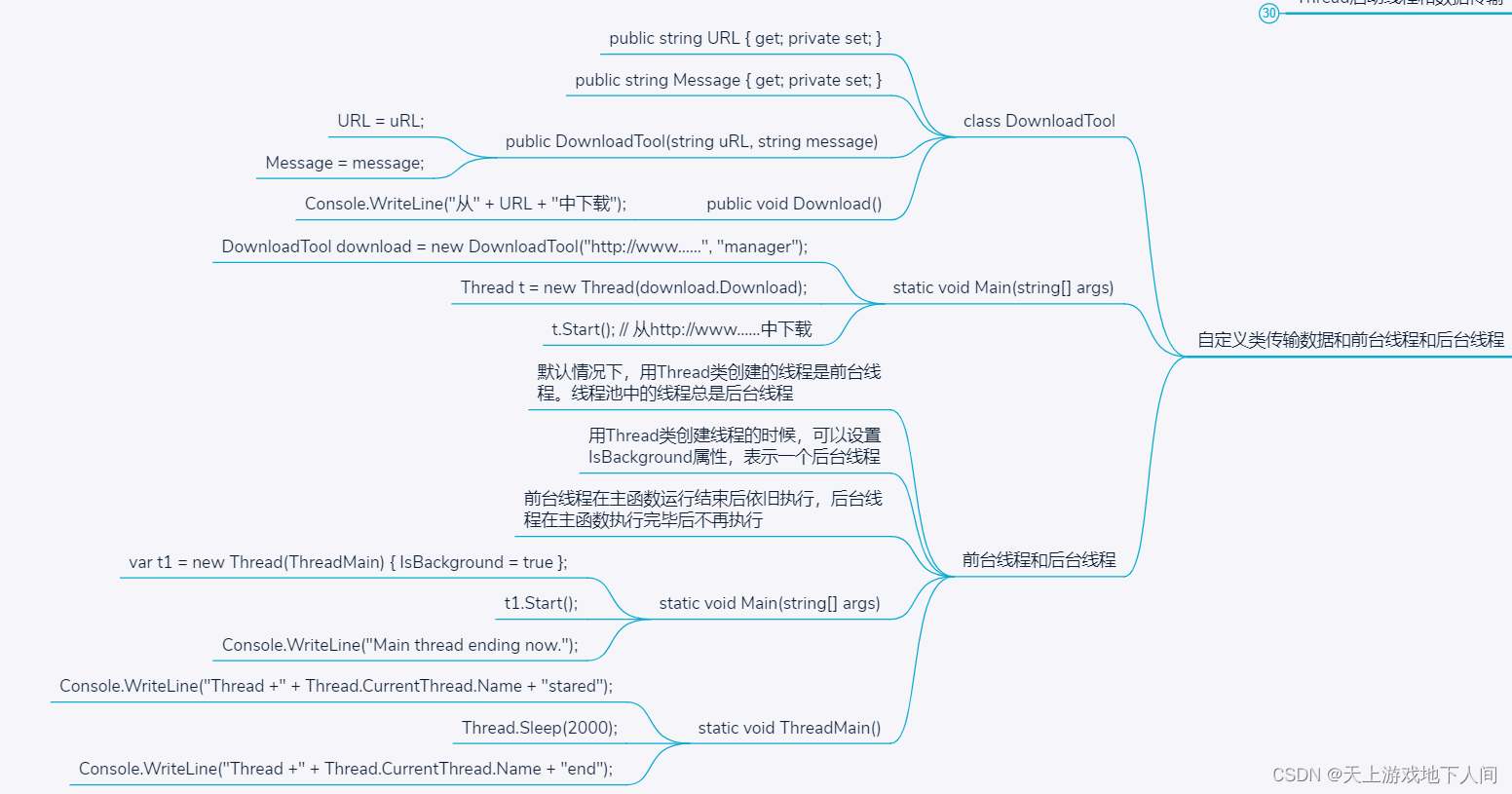
C#__自定义类传输数据和前台线程和后台线程
// 前台线程和后台线程 // 默认情况下,用Thread类创建的线程是前台线程。线程池中的线程总是后台线程。 // 用Thread类创建线程的时候,可以设置IsBackground属性,表示一个后台线程。 // 前台线程在主函数运行结束后依旧执行,后台线…...
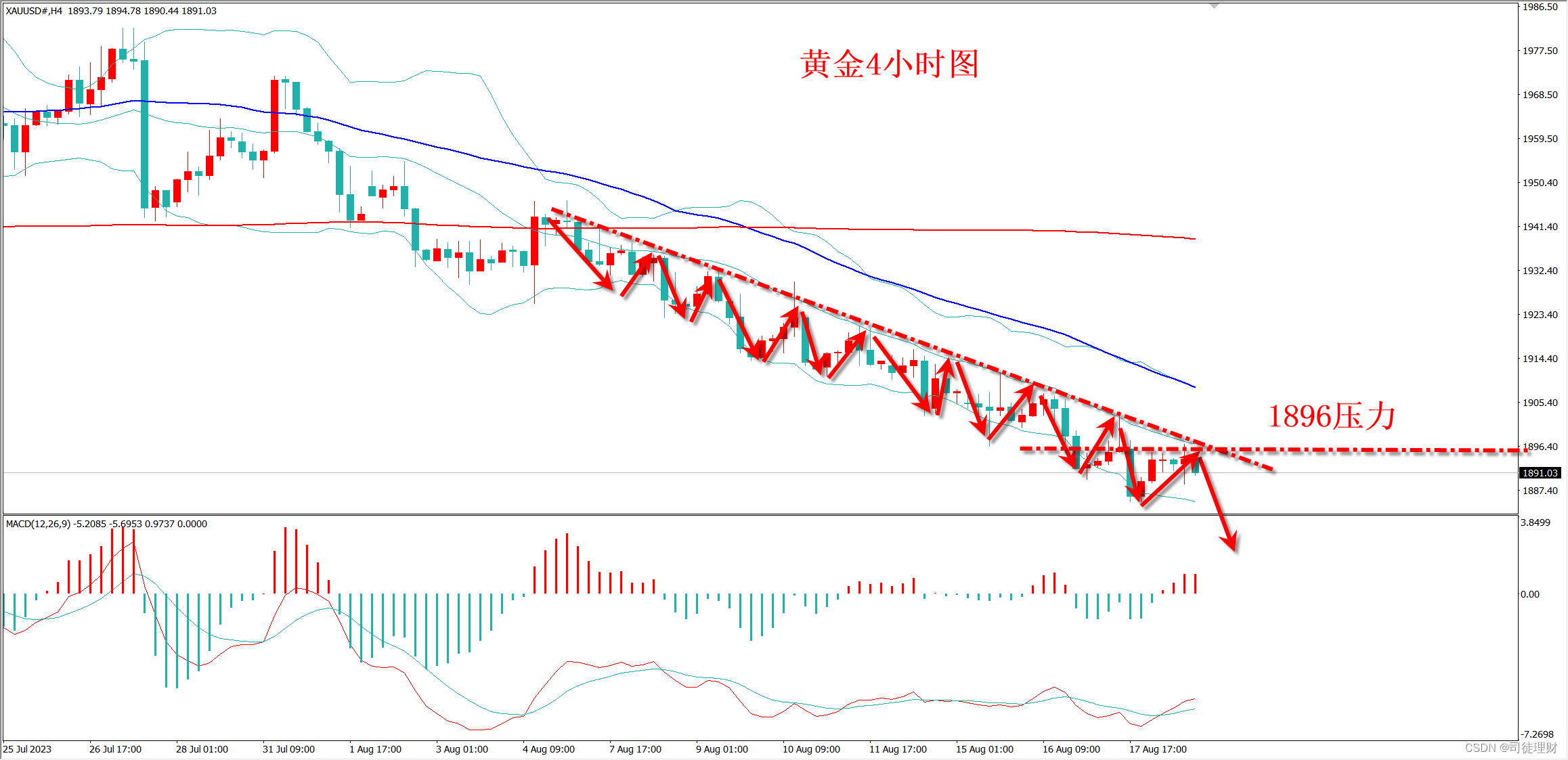
司徒理财:8.21黄金空头呈阶梯下移!今日操作策略
黄金走势分析 盘面裸k分析:1小时周期的行情局部于1896附近即下行通道上轨附近录得一系列的K线呈震荡下行并筑圆顶,上轨压制有效,下行通道并未突破,后市建议延续看下行。4小时周期局部录得一系列的纺锤线呈震荡,但行情整…...

Java8 实现批量插入和更新,SpringBoot实现批量插入和更新,Mybatis实现批量插入和更新
前言 基于mybatis实现的批量插入和更新 由于直接执行批量所有数据可能会出现长度超出报错问题,使用如下方式即可解决 实现 原理还是分配执行,这里的100就是设定每次执行最大数 /*** 封装使用批量添加或修改数据库操作* * param list 集合* param inse…...
vue登录验证码组件,前端验证
效果图 点击可以切换验证码 自定义组件 <template><div class"s-canvas"><canvas id"s-canvas" :width"contentWidth" :height"contentHeight"></canvas></div> </template> <script> e…...
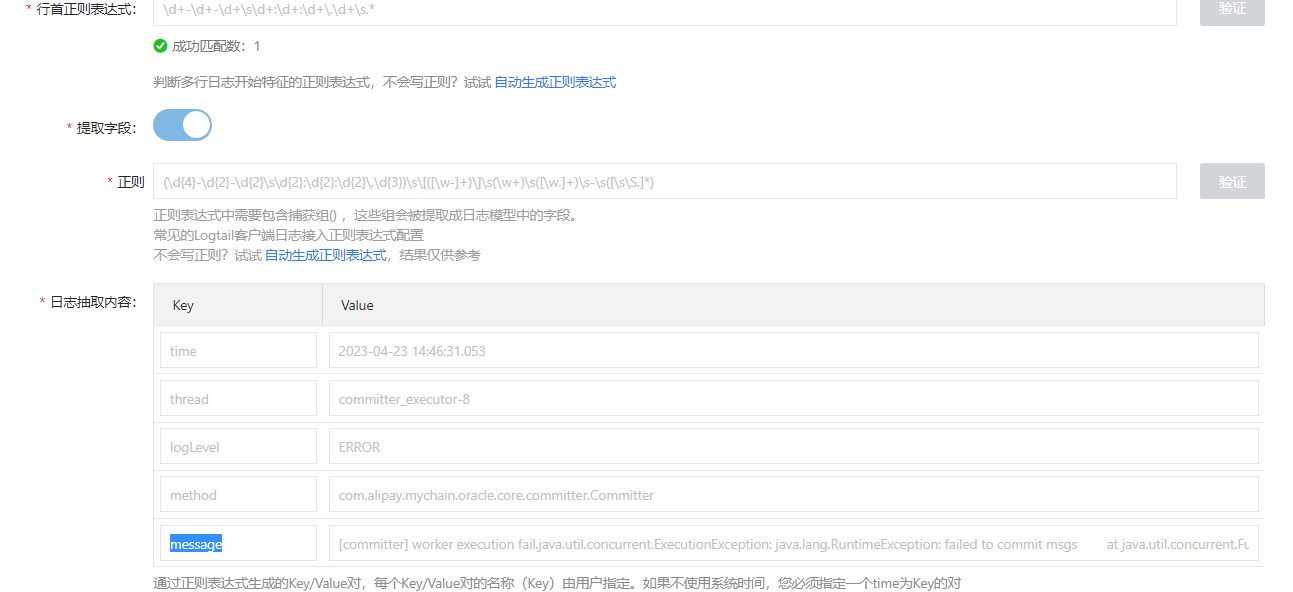
SLS日志解析配置
分隔符模式 INFO|2023-04-10T11:05:30.12808:00|X.X.X.X|ACCESS_ALLOWED|1 模式:分隔符模式 日志样例:贴文档说明中的样例,或者直接在SLS历史日志里找一行 分隔符:竖线 日志抽取内容Key用文档中说明的变量名 是否接受部分字段&am…...
CRM系统有哪些功能可以管理客户?
客户管理,可以简单理解为企业收集并利用客户信息,建立与客户的良好关系,满足客户的需求,从而提升客户价值的过程。CRM一直被誉为客户管理的“神器”,下面我们就来说说,什么是客户管理?CRM如何管…...
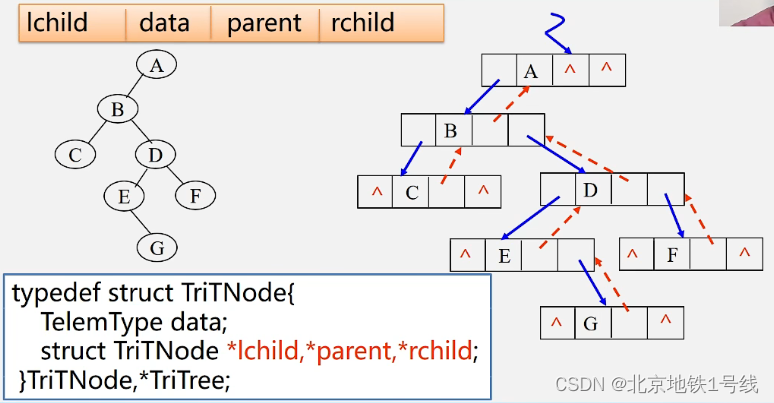
15.树与二叉树基础
目录 一. 树,基本术语 二. 二叉树 (1)二叉树 (2)满二叉树 (3)完全二叉树 三. 二叉树的性质 四. 二叉树的存储结构 (1)顺序存储结构 (2)链…...
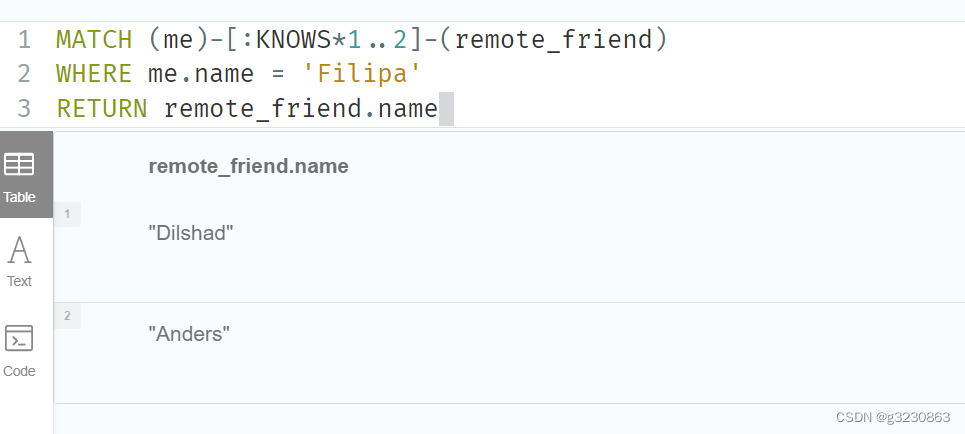
neo4j 图数据库 springboot
一.安装 neo4j社区版在liunx安装部署 https://blog.csdn.net/u013946356/article/details/81736232 二.知识图数据导入 参考:https://notemi.cn/neo4j-import-csv-file-data.html http://openkg.cn/dataset/ch4masterpieces 放在对应的import文件夹下面 导入数据 LOAD C…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...