15.树与二叉树基础
目录
一. 树,基本术语
二. 二叉树
(1)二叉树
(2)满二叉树
(3)完全二叉树
三. 二叉树的性质
四. 二叉树的存储结构
(1)顺序存储结构
(2)链式存储结构
树形结构:结点之间有分支,具有层次关系。
一. 树,基本术语
树的定义:树(Tree)是n (n≥0)个结点的有限集。
(1)若n = 0,称为空树;
(2)若n >0,则它满足如下两个条件:
- 有且仅有一个特定的称为根(Root)的结点;
- 其余结点可分为m(m≥0)个互不相交的有限集T1,T2,T3,....Tm,其中每一个集合本身又是一棵树,并称为根的子树(SubTree)。


树的一些基本术语在下图中展示:
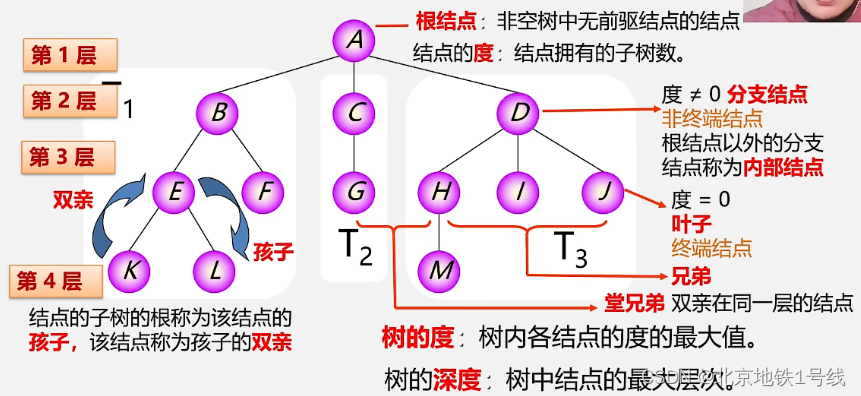
有序树:树中结点的各子树从左至右有次序(最左边的为第一个孩子)。
无序树:树中结点的各子树无次序。
森林:是m(m≥O)棵互不相交的树的集合。
森林与树的关系:把树的根结点删除树就变成了森林。一棵树可以看成是一个特殊的森林。给森林中的各子树加上一个双亲结点,森林就变成了树。

二. 二叉树
(1)二叉树
为何要重点研究每结点最多只有两个“叉”的树?
- 二叉树的结构最简单,规律性最强;
- 可以证明,所有树都能转为唯一对应的二叉树,不失一般性。
普通树(多叉树)若不转化为二叉树,则运算很难实现。二叉树在树结构的应用中起着非常重要的作用,因为对二叉的许多操作算法简单,而任何树都可以与二叉树相互转换,这样就解决了。
二叉树:二叉树是n(n≥0)个结点的有限集,它或者是空集(n = 0),或者由一个根结点及两棵互不相交的,分别称作这个根的左子树和右子树的二叉树组成。
二叉树的特点:
- 每个结点最多有俩孩子(二叉树中不存在度大于2的结点)。
- 子树有左右之分,其次序不能颠倒。
- 二叉树可以是空集合,根订以有空的左子树或空的右子树。
注意:二叉树不是树的特殊情况,也不是有序树,而是两个不同的概念。
- 二叉树结点的子树要区分左子树和右子树,即使只有一棵子树也行区分,说明它是左子树,还是右子树。
- 树当结点只有一个孩子时,就无须区分它是左还是右的次序。因此二者是不同的。这是二叉树与树的最主要的差别。
也就是二叉树每个结点位置或者说次序都是固定的,可以是空,但是不可以说它没有位置,而树的结点位置是相对于别的结点来说的,没有别的结点时,它就无所谓左右了。
二叉树的五种基本形态如下:
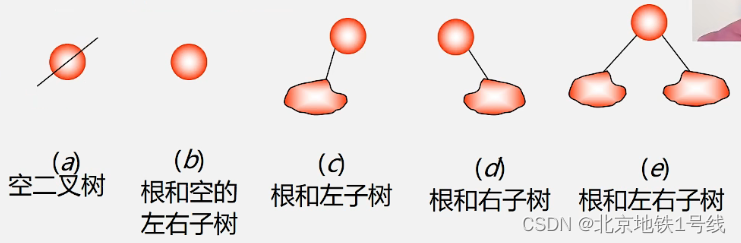
下面我们介绍满二叉树和完全二叉树,这两种特殊的二叉树在顺序存储结构下可以复原。
(2)满二叉树
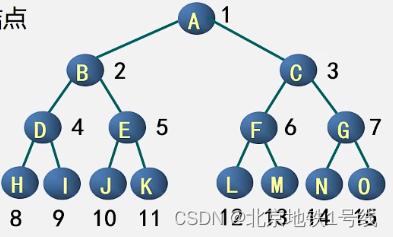
一棵深度为k且有个结点的二叉树称为满二叉树。
特点:1.每一层上的结点数都是最大结数(即每层都满);2.叶子节点全部在最底层; 3.满二叉树在同样深度的二叉树中,结点数,叶子结点数都是最多的。
对满二叉树结点位置进行编号:从根结点开始,自上而下,自左而右。每一结点位置都有元素。
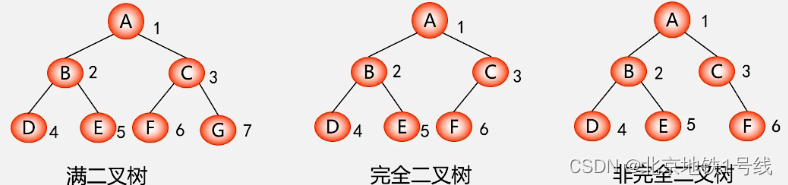
(3)完全二叉树
深度为k的具有n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树中编号为1~n的结点一一对应时,称之为完全二叉树。
也可以从满二叉树看完全二叉树:在满二叉树中,从最后一个结点开始,连续去掉任意个结点,即是一棵完全二叉树。一定是连续的去掉!
特点:1.叶子结点只可能分布在层次最大的两层上;2.对任一结点,如果其右子树的最大层次为i,则其左子树的最大层次必为i或i+1。
三. 二叉树的性质
性质1:二叉树的第i层上最多有个结点(i>=1),最少有1个结点;
性质2:深度为k的二叉树至多有个结点,最少有k个结点;
性质3:对任何一个二叉树T,如果叶子结点数为n0,度为2的结点数为n2,则有:;
证明:设总边数为B,结点数为n,显然有:,这是由于除了根结点以外,每个结点有且只有一个前驱。
同时,因为结点的度只能为0,1,2,记他们的个数分别是,所以有:
和
;
联立以上三式就可得到:,证毕。
性质4:具有n个结点的完全二叉树的深度是,其中
表示不超过x的最大整数。
证明:深度为k的完全二叉树,结点个数的范围是:
性质5:对一个具有n个结点的完全二叉树,对一个编号为i的结点:
(1)i>1时,此结点的双亲结点是;
(2)此结点的左孩子结点编号是,右孩子结点编号是
(如果左右孩子存在);
四. 二叉树的存储结构
(1)顺序存储结构
实现:按满二叉树的结点层次编号,依次存放二叉树中的数据元素。
//二叉树的顺序存储
# define MAXSIZE 100
typedef TElemType SqBiTree[MAXSIZE];
SqBiTree bt;定义二叉树的顺序存储结构如上所示,使用了一个数组 SqBiTree 来表示二叉树。SqBiTree 是一个 typedef 定义的类型别名,它是一个大小为 MAXSIZE 的数组,数组元素的类型是 TElemType。TElemType 可以根据具体的需求来定义,表示二叉树节点的数据类型。在这段代码中没有给出 TElemType 的具体定义,需要根据实际情况来确定。通过这段代码,我们可以使用数组 bt 来表示一个二叉树,数组的大小为 MAXSIZE,数组中的元素存储了二叉树的节点数据。这种顺序存储结构的好处是可以快速访问二叉树的任意节点,但是需要提前确定二叉树的最大节点数。

例:根据数组还原二叉树
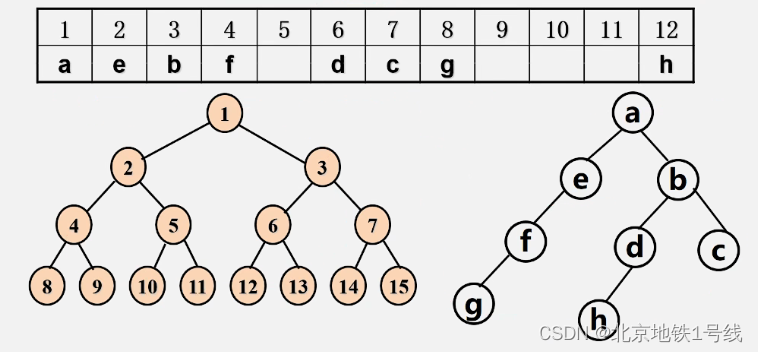
特点:结点间关系蕴含在数组位置中,浪费空间,适用于满二叉树和完全二叉树。
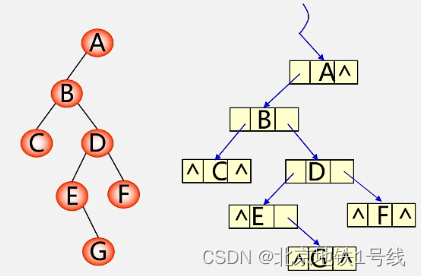
(2)链式存储结构
二叉树结点的特点:每个结点有左孩子,或者右孩子,所以二叉树的链式结点包含数据域和两个指针域:

typedef struct BiNode{TElemType data;struct BiNode *lchild,*rchild; //左右孩子指针
}BiNode,*BiTree;
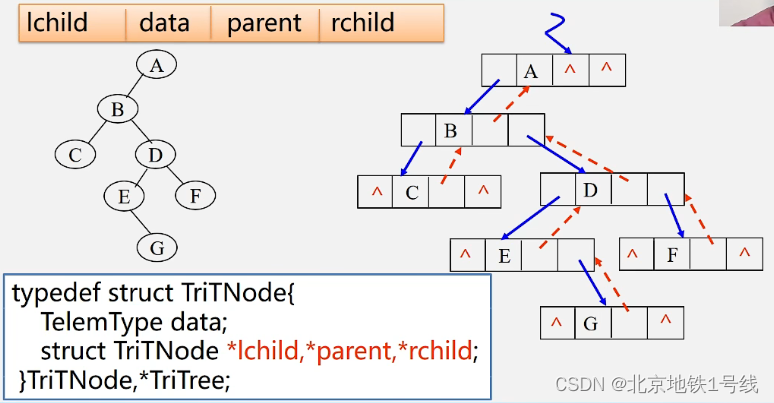
有时为了寻找祖先结点,还会增设一个指针*parent,这样结点就有四部分:
| lchild | data | parent | rchild |
相关文章:

15.树与二叉树基础
目录 一. 树,基本术语 二. 二叉树 (1)二叉树 (2)满二叉树 (3)完全二叉树 三. 二叉树的性质 四. 二叉树的存储结构 (1)顺序存储结构 (2)链…...
neo4j 图数据库 springboot
一.安装 neo4j社区版在liunx安装部署 https://blog.csdn.net/u013946356/article/details/81736232 二.知识图数据导入 参考:https://notemi.cn/neo4j-import-csv-file-data.html http://openkg.cn/dataset/ch4masterpieces 放在对应的import文件夹下面 导入数据 LOAD C…...
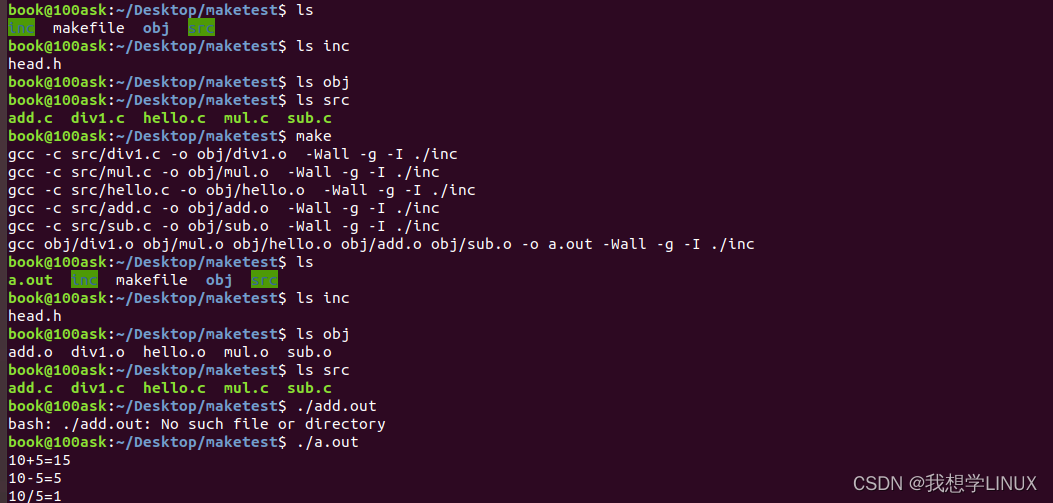
Linux下的系统编程——makefile入门(四)
前言: 或许很多Winodws的程序员都不知道这个东西,因为那些Windows的IDE都为你做了这个工作,但我觉得要作一个好的和professional的程序员,makefile还是要懂。这就好像现在有这么多的HTML的编辑器,但如果你想成为一个专…...

Mybatis的综合案例-学生信息查询系统 用于校验是否真正学习掌握了动态SQL
Mybatis的综合案例-学生信息查询系统 需求一:当用户输入的学生姓名不为空,则只根据学生信息进行查询; 当用户输入的学生姓名为空,且专业不为空,那么就根据学生专业进行学生的查询 需求二:查询所有id值小于5的学生信息…...
)
力扣:70. 爬楼梯(Python3)
题目: 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 来源:力扣(LeetCode) 链接:力扣(LeetCode)官网 - 全球极客…...
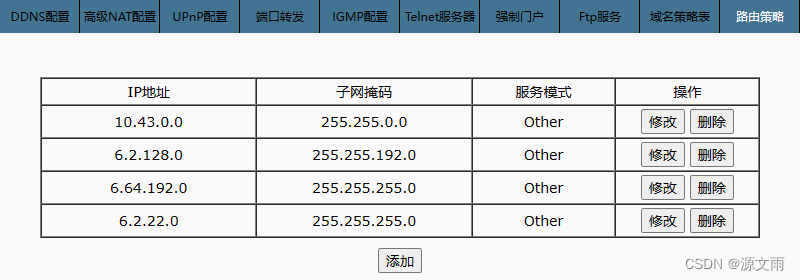
陕西广电 HG6341C FiberHome烽火 光猫获取超级密码 改桥接模式 提升网速
光猫默认的路由模式实测在100M宽带下只能跑到60M左右,只有改成桥接模式才能跑满,不损失性能。但是改桥接需要给运营商打电话,有的时候不想麻烦他们,这时获取超级密码进行更改就是一个不错的选择了 分析 之前写了一篇HGU B2 光猫的…...

无涯教程-PHP - 移除的扩展
以下扩展已从PHP 7开始删除- eregmssqlmysqlsybase_ct 以下SAPI已从PHP 7开始删除- aolserverapacheapache_hooksapache2filtercaudiumcontinuityisapimilternsapiphttpdpi3webroxenthttpdtuxwebjames PHP - 移除的扩展 - 无涯教程网无涯教程网提供以下扩展已从PHP 7开始删除…...
笔记:transformer系列
1、和其他网络的比较 自注意力机制适合处理长文本,并行度好,在GPU上,CNN和Self-attention性能差不多,在TPU(Tensor Processing Uni)效果更好。 总结: 自注意力池化层将当做key,value,query来…...

Mysql socket连接测试
配置如下: socket /data/mysql/data/mysql.sock //套接字文件 在数据库没有任何连接的情况下,可以看到3306端口和socket端口都在监听 [mysqlt3-dtpoc-dtpoc-web04 bin]$ netstat -an | grep -i 3306 tcp 0 0 0.0.0.0:3306 0.…...

探究分布式操作系统的本质
探究分布式操作系统的本质 有一位网友问,分布式操作系统的本质是什么,今天就来说说这个话题。 首先,我们需要明确什么是分布式操作系统。 从大范围来理解,分布式操作系统是传统单机操作系统的延伸,可以看作是在多台独…...
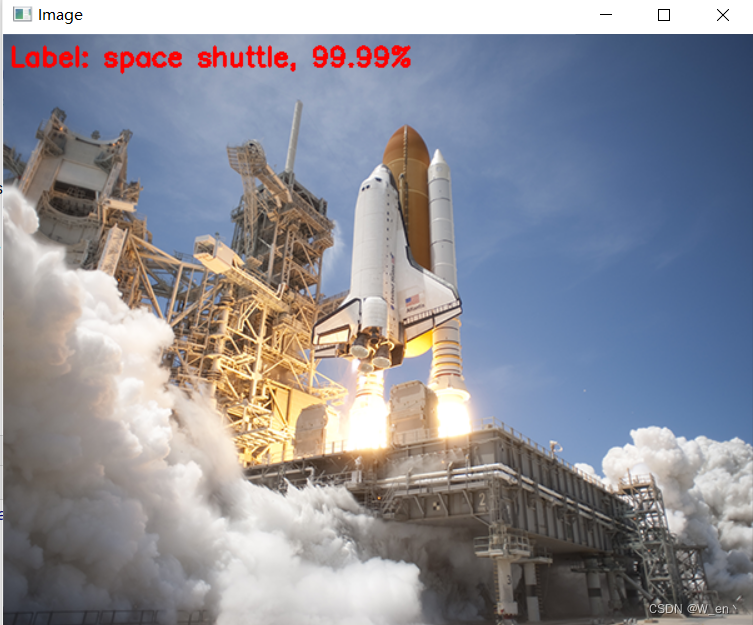
opencv-dnn
# utils_words.txt 标签文件 import osimage_types (".jpg", ".jpeg", ".png", ".bmp", ".tif", ".tiff")def list_images(basePath, containsNone):# return the set of files that are validreturn list_file…...

如何选择合适的开源许可证?
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

【前端】深入解析CSS:选择器、显示模式、背景属性和特征剖析
目录 一、前言二、CSS的复合选择器1、后代选择器①、语法②、注意事项 2、子选择器①、语法②、注意事项 3、并集选择器①、语法②、注意事项 4、链接伪类选择器①、语法②、注意事项 三、CSS元素显示模式转换1、转换为块元素display:block2、转换为行内元素display:inline3、转…...
| 动态规划Part04:01背包)
算法训练营第三十四天(8.23)| 动态规划Part04:01背包
目录 Leecode 1049.最后一块石头的重量II Leecode 494.目标和 Leecode 474.一和零 Leecode 1049.最后一块石头的重量II 题目地址:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 题目类型:01背包 class Solution { public:int…...

【python】tkinter使用多进程打包成exe后multiprocessing无法关闭对应进程
这是由于multiprocessing模块在Windows操作系统下使用fork方法创建子进程时会导致打包成exe后无法正常运行的问题。 可以尝试使用freeze_support函数来解决这个问题。freeze_support函数是在Windows操作系统下用于支持multiprocessing模块的函数。 下面是一个示例代码&#x…...
)
Redis工具类(缓存操作,Object转换成JSON数据)
依赖spring-data-redis-2.4.1.jar Component Data public class RedisUtils {Autowiredprivate RedisTemplate<String, Object> redisTemplate;Resource(name "stringRedisTemplate")private ValueOperations<String, String> valueOperations;/*** 默…...

Linux 下 Java Socket 编程报 java.net.Exception:Permission denied (权限不足)
本人用Linux部署springboot项目时遇见这个错误,原因很简单,就是端口号没有选对。 在linux系统中,端口号再1024以下的需要root权限,只要把端口改成大于1024的就可以了,但避开一些软件的默认端口,如Tomcat的8…...
IDEA项目实践——VUE介绍与案例分析
系列文章目录 IDEA项目实践——JavaWeb简介以及Servlet编程实战 IDEA项目实践——Spring集成mybatis、spring当中的事务 IDEA项目实践——Spring当中的切面AOP IDEWA项目实践——mybatis的一些基本原理以及案例 IDEA项目实践——Spring框架简介,以及IOC注解 I…...

vue-canvas基本使用和注意事项-动画闪烁效果-自适应适配不同分辨率问题
前言 canvas画布是html的新特性,熟悉画布我们可以完成很多拖拽,标注,动画的功能 使用canvas实现一个小例子很容易,但是真正在项目中使用时,我们需要注意的地方有很多 canvas基本原理就是它基于渲染方法,根…...

Jmeter 如何才能做好接口测试?
现在对测试人员的要求越来越高,不仅仅要做好功能测试,对接口测试的需求也越来越多! 所以也越来越多的同学问,怎样才能做好接口测试? 要真正的做好接口测试,并且弄懂如何测试接口,需要从如下几…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

归并排序:分治思想的高效排序
目录 基本原理 流程图解 实现方法 递归实现 非递归实现 演示过程 时间复杂度 基本原理 归并排序(Merge Sort)是一种基于分治思想的排序算法,由约翰冯诺伊曼在1945年提出。其核心思想包括: 分割(Divide):将待排序数组递归地分成两个子…...
