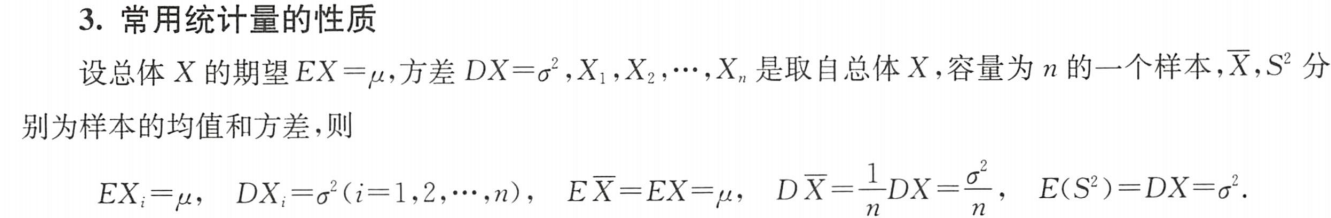概率论与数理统计:第六章:数理统计
文章目录
- Ch6. 数理统计
- (一) 总体与样本
- (二) 统计量 (5个)
- 2.5个常用统计量
- 3.矩的概念
- (三) 抽样分布 (3个)
- 0.上α分位点
- 1.χ²分布
- 2.t分布
- 3.F分布
- (四) 抽样分布定理
- 1.单个正态总体
- 2.两个正态总体
Ch6. 数理统计
(一) 总体与样本
1.概念:
(1)总体

(2)样本
简单随机样本,简称样本。样本与总体 独立同分布。(取自总体的样本,相互之间都独立,且与总体分布相同)

(3)样本的分布

2.性质:
设 X 1 , X 2 , X 3 , . . . , X n ( n > 1 ) X_1,X_2,X_3,...,X_n(n>1) X1,X2,X3,...,Xn(n>1)为来自总体 N(μ,σ²) (σ>0)的简单随机样本(独立同分布), X ‾ = 1 n ∑ i = 1 n X i \overline{X}=\dfrac{1}{n}\sum\limits_{i=1}^nX_i X=n1i=1∑nXi,则有:
① X i ∼ N ( μ , σ 2 ) X_i\sim N(μ,σ²) Xi∼N(μ,σ2)
② X ‾ ∼ N ( μ , σ 2 n ) \overline{X} \sim N(μ,\dfrac{σ²}{n}) X∼N(μ,nσ2)
③ C o v ( X i , X ‾ ) = σ 2 n {\rm Cov}(X_i,\overline{X})=\dfrac{σ²}{n} Cov(Xi,X)=nσ2
证明:
3.样本与总体 独立同分布,期望相同,方差也相同
①样本的期望与总体的期望相同: E ( X i ) = E ( X ) E(X_i) = E(X) E(Xi)=E(X), ∑ i = 1 n E ( X i ) = n E ( X ) \sum\limits_{i=1}^nE(X_i) = nE(X) i=1∑nE(Xi)=nE(X)
②样本的方差与总体的方差相同: D ( X i ) = D ( X ) D(X_i) = D(X) D(Xi)=D(X), ∑ i = 1 n D ( X i ) = n D ( X ) \sum\limits_{i=1}^nD(X_i) = nD(X) i=1∑nD(Xi)=nD(X)
例题1:18年23(2)
例题2:16年23(1)
(二) 统计量 (5个)
1.概念
(1)统计量的定义

(2)顺序统计量
| 顺序统计量 | 定义 | 分布函数 | 概率密度 |
|---|---|---|---|
| ①第n顺序统计量 X ( n ) X_{(n)} X(n) | m a x { X 1 , X 2 , . . . , X n } max\{X_1,X_2,...,X_n\} max{X1,X2,...,Xn} | [ F ( x ) ] n [F(x)]^n [F(x)]n | n [ F ( x ) ] n − 1 f ( x ) n[F(x)]^{n-1}f(x) n[F(x)]n−1f(x) |
| ②第1顺序统计量 X ( 1 ) X_{(1)} X(1) | m i n { X 1 , X 2 , . . . , X n } min\{X_1,X_2,...,X_n\} min{X1,X2,...,Xn} | 1 − [ 1 − F ( x ) ] n 1-[1-F(x)]^n 1−[1−F(x)]n | n [ 1 − F ( x ) ] n − 1 f ( x ) n[1-F(x)]^{n-1}f(x) n[1−F(x)]n−1f(x) |

2.5个常用统计量
①样本均值: X ˉ = 1 n ∑ i = 1 n X i \bar{X}=\dfrac{1}{n}\sum\limits_{i=1}^nX_i Xˉ=n1i=1∑nXi ∴ ∑ i = 1 n X i = n X ˉ \sum\limits_{i=1}^nX_i=n\bar{X} i=1∑nXi=nXˉ
②样本方差: S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ˉ ) 2 S²=\dfrac{1}{n-1}\sum\limits_{i=1}^n(X_i-\bar{X})² S2=n−11i=1∑n(Xi−Xˉ)2 = 1 n − 1 ( ∑ i = 1 n X i 2 − n X ˉ 2 ) =\dfrac{1}{n-1}(\sum\limits_{i=1}^nX_i^2-n\bar{X}^2) =n−11(i=1∑nXi2−nXˉ2), E ( S 2 ) = σ 2 E(S^2)=σ² E(S2)=σ2
样本标准差: S = 1 n − 1 ∑ i = 1 n ( X i − X ˉ ) 2 S=\sqrt{\dfrac{1}{n-1}\sum\limits_{i=1}^n(X_i-\bar{X})²} S=n−11i=1∑n(Xi−Xˉ)2
③样本k阶(原点)矩: A k = 1 n ∑ i = 1 n X i k ( k = 1 , 2 , . . . ) A_k=\dfrac{1}{n}\sum\limits_{i=1}^nX_i^k (k=1,2,...) Ak=n1i=1∑nXik(k=1,2,...)
④样本k阶中心矩: B k = 1 n ∑ i = 1 n ( X i − X ˉ ) k ( k = 2 , 3 , . . . ) B_k=\dfrac{1}{n}\sum\limits_{i=1}^n(X_i-\bar{X})^k(k=2,3,...) Bk=n1i=1∑n(Xi−Xˉ)k(k=2,3,...)
①k阶原点矩是 ( X i − 0 ) k (X_i-0)^k (Xi−0)k,k阶中心矩是 ( X i − X ˉ ) k (X_i-\bar{X})^k (Xi−Xˉ)k
②样本均值是一阶原点矩,二阶中心矩 B 2 = 1 n ∑ i = 1 n ( X i − X ˉ ) 2 = n − 1 n S 2 B_2=\dfrac{1}{n}\sum\limits_{i=1}^n(X_i-\bar{X})²=\dfrac{n-1}{n}S^2 B2=n1i=1∑n(Xi−Xˉ)2=nn−1S2
3.矩的概念
①原点矩 A
| 样本k阶原点矩 A k A_k Ak | 总体k阶原点矩 |
|---|---|
| A 1 = 1 n ∑ i = 1 n X i = X ˉ A_1=\dfrac{1}{n}\sum\limits_{i=1}^nX_i=\bar{X} A1=n1i=1∑nXi=Xˉ (样本一阶原点矩,即为均值) | E(X) |
| A 2 = 1 n ∑ i = 1 n X i 2 A_2=\dfrac{1}{n}\sum\limits_{i=1}^nX_i^2 A2=n1i=1∑nXi2 | E(X²) |
| … | … |
| A k = 1 n ∑ i = 1 n X i k , k = 1 , 2 , . . . A_k=\dfrac{1}{n}\sum\limits_{i=1}^nX_i^k,k=1,2,... Ak=n1i=1∑nXik,k=1,2,... | E(Xk) |
②中心距 B
| 样本k阶中心矩 B k B_k Bk | 总体k阶中心矩 |
|---|---|
| B 1 = 1 n ∑ i = 1 n ( X i − X ˉ ) B_1=\dfrac{1}{n}\sum\limits_{i=1}^n(X_i-\bar{X}) B1=n1i=1∑n(Xi−Xˉ) | E ( X − E X ) E(X-EX) E(X−EX) |
| B 2 = 1 n ∑ i = 1 n ( X i − X ˉ ) 2 = n − 1 n S 2 B_2=\dfrac{1}{n}\sum\limits_{i=1}^n(X_i-\bar{X})²=\dfrac{n-1}{n}S^2 B2=n1i=1∑n(Xi−Xˉ)2=nn−1S2 | E [ ( X − E X ) 2 ] = D X E[(X-EX)²]=DX E[(X−EX)2]=DX |
| … | … |
| B k = 1 n ∑ i = 1 n ( X i − X ˉ ) k B_k=\dfrac{1}{n}\sum\limits_{i=1}^n(X_i-\bar{X})^k Bk=n1i=1∑n(Xi−Xˉ)k | E [ ( X − E X ) k ] E[(X-EX)^k] E[(X−EX)k] |
总体矩的矩估计量为样本矩:
①EX的矩估计量为 A 1 = 1 n ∑ i = 1 n X i = X ˉ A_1=\dfrac{1}{n}\sum\limits_{i=1}^nX_i=\bar{X} A1=n1i=1∑nXi=Xˉ
②DX的矩估计量为 B 2 = 1 n ∑ i = 1 n ( X i − X ˉ ) 2 = n − 1 n S 2 B_2=\dfrac{1}{n}\sum\limits_{i=1}^n(X_i-\bar{X})²=\dfrac{n-1}{n}S^2 B2=n1i=1∑n(Xi−Xˉ)2=nn−1S2
(三) 抽样分布 (3个)
三大抽样分布,均与正态总体有关。总体与样本服从标准正态分布N(0,1)。
0.上α分位点
正态分布的上α分位点: Φ ( Z α 2 ) = 1 − α 2 Φ(Z_{\frac{α}{2}})=1-\dfrac{α}{2} Φ(Z2α)=1−2α


1.χ²分布
1.χ²分布的定义
若 X 1 ∼ N ( 0 , 1 ) X_1\sim N(0,1) X1∼N(0,1),则 X 1 2 ∼ χ 2 ( 1 ) X_1^2\sim χ^2(1) X12∼χ2(1)
设X1,X2,…,Xn为正态总体N(0,1)的样本 ( X i X_i Xi相互独立且同分布),则把统计量
χ 2 = X 1 2 + X 2 2 + . . . + X n 2 χ^2=X_1^2+X_2^2+...+X_n^2 χ2=X12+X22+...+Xn2
服从的分布称为 自由度为n的χ²分布,记作 χ²~χ²(n)
2.χ²分布的上α分位点
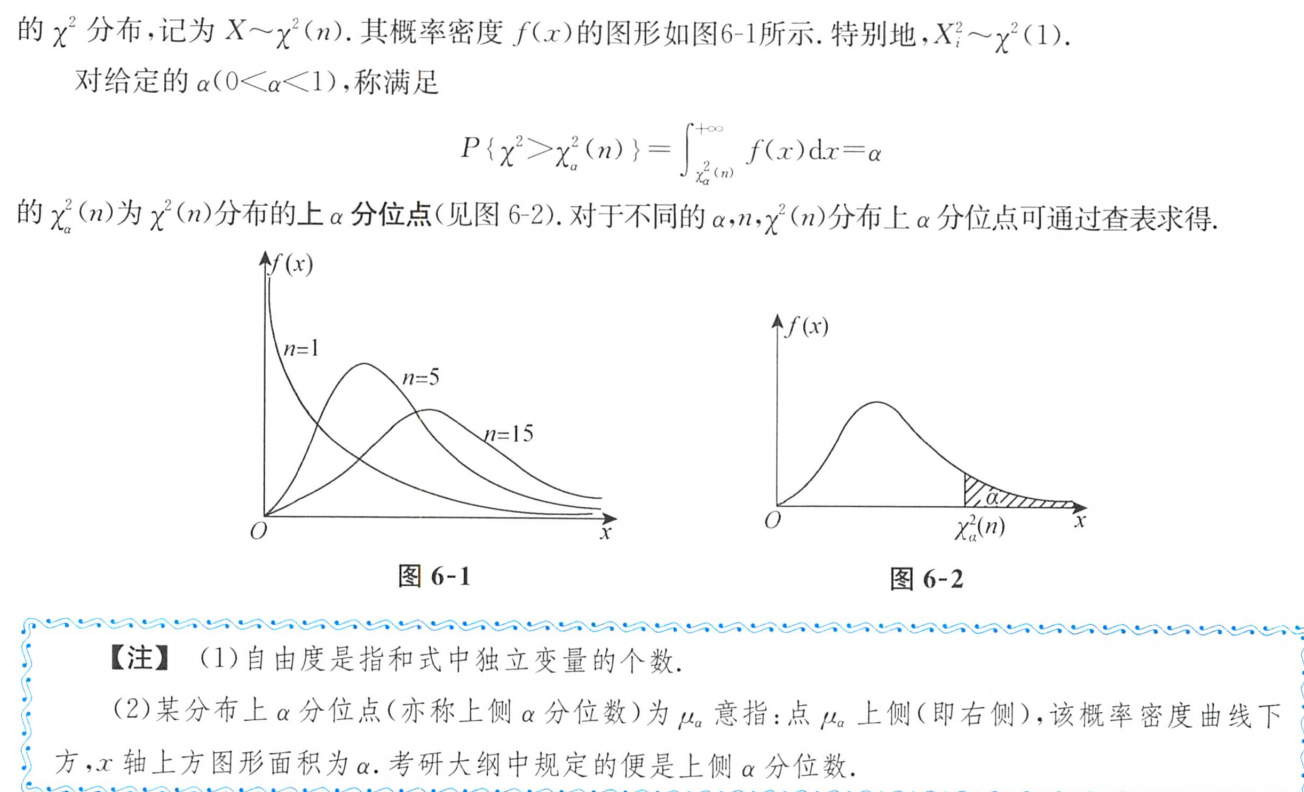
3.χ²分布的性质
- χ²分布的数字特征: E(χ²)=n,D(χ²)=2n
- χ²分布的独立可加性:设 χ 1 2 ∼ χ 2 ( n 1 ) , χ 2 2 ∼ χ 2 ( n 2 ) χ²_1\sim χ²(n_1),χ²_2\sim χ²(n_2) χ12∼χ2(n1),χ22∼χ2(n2),且 χ 1 2 χ²_1 χ12与 χ 2 2 χ²_2 χ22相互独立,则 χ 1 2 + χ 2 2 ∼ χ 2 ( n 1 + n 2 ) χ²_1+χ²_2\simχ²(n_1+n_2) χ12+χ22∼χ2(n1+n2)
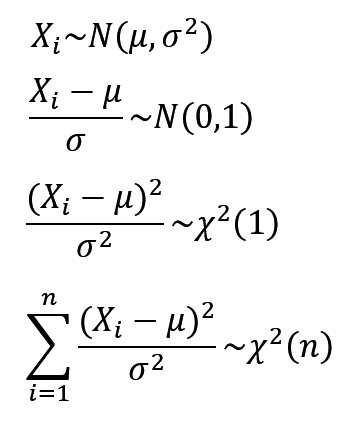
例题1:

分析:

答案: 1 20 \dfrac{1}{20} 201、 1 100 \dfrac{1}{100} 1001、2
例题2:11年23.(2)
2.t分布
1.t分布定义
设 X ∼ N ( 0 , 1 ) , Y ∼ χ 2 ( n ) X\sim N(0,1), Y\sim χ^2(n) X∼N(0,1),Y∼χ2(n),且X,Y相互独立,则把统计量 t = X Y n t=\dfrac{X}{\sqrt{\dfrac{Y}{n}}} t=nYX
服从的分布称为自由度为n的t分布,记作 t ∼ t ( n ) t\sim t(n) t∼t(n)
t(n)的概率密度h(t)关于t=0对称。当自由度n→∞时,t分布的极限就是标准正态分布,n≥30即可
2.t分布的上α分位点
x = t α ( n ) x=t_α(n) x=tα(n)右侧的面积(概率)为α,则称 t α ( n ) t_α(n) tα(n)为上α分位点
x = t 1 − α ( n ) x=t_{1-α}(n) x=t1−α(n)右侧的面积(概率)为1-α,则称 t 1 − α ( n ) t_{1-α}(n) t1−α(n)为上1-α分位点
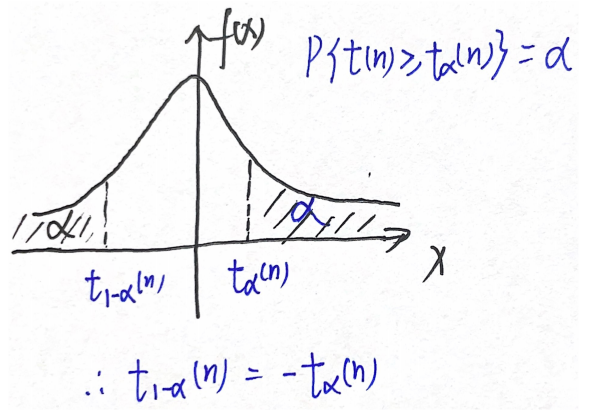
t分布的概率密度是偶函数
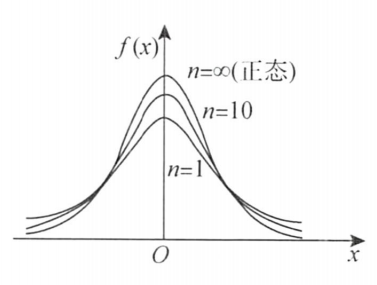
3.t分布性质
1. E ( t ) = 0 E(t)=0 E(t)=0
2.上α分位点: t 1 − α ( n ) = − t α ( n ) t_{1-α}(n)=-t_α(n) t1−α(n)=−tα(n)
3.F分布
1.F分布定义
设 X ∼ χ 2 ( n 1 ) , Y ∼ χ 2 ( n 2 ) X\sim χ^2(n_1),Y\sim χ^2(n_2) X∼χ2(n1),Y∼χ2(n2),且X,Y相互独立,则把随机变量 F = X n 1 Y n 2 F=\dfrac{\dfrac{X}{n_1}}{\dfrac{Y}{n_2}} F=n2Yn1X
服从的分布称为自由度为(n1,n2)的F分布,其中n1称为第一自由度,n2称为第二自由度,记作 F ∼ F ( n 1 , n 2 ) F\sim F(n_1,n_2) F∼F(n1,n2)
2.F分布性质
1.若 F ∼ F ( n 1 , n 2 ) F\sim F(n_1,n_2) F∼F(n1,n2),则 1 F ∼ F ( n 2 , n 1 ) \dfrac{1}{F}\sim F(n_2,n_1) F1∼F(n2,n1)
2.上α分位点: 1 F α ( n 1 , n 2 ) = F 1 − α ( n 2 , n 1 ) \dfrac{1}{F_α(n_1,n_2)}=F_{1-α}(n_2,n_1) Fα(n1,n2)1=F1−α(n2,n1)
3.t分布与F分布的关系
若 t ∼ t ( n ) ,则 t 2 ∼ F ( 1 , n ) , 1 t 2 ∼ F ( n , 1 ) 若t\sim t(n),则t^2\sim F(1,n),\dfrac{1}{t^2}\sim F(n,1) 若t∼t(n),则t2∼F(1,n),t21∼F(n,1)
例题1:03年12. t分布与F分布的关系

分析:
X ∼ t ( n ) , X 2 ∼ F ( 1 , n ) , 1 X 2 ∼ F ( n , 1 ) X\sim t(n),X²\sim F(1,n),\dfrac{1}{X²}\sim F(n,1) X∼t(n),X2∼F(1,n),X21∼F(n,1)
答案:C
例题2:13年8.
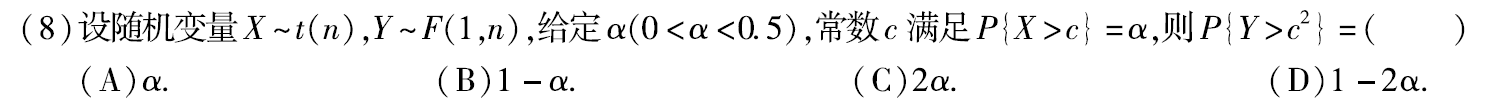
分析:X~t(n), 则 X²=Y~F(1,n)
∴P{Y>c²}=P{X²>c²}=P{X>c}+P{X<-c}=α+α=2α
答案:C
(四) 抽样分布定理
设总体 X ∼ N ( μ , σ 2 ) X\sim N(μ,σ²) X∼N(μ,σ2),样本为 X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn,独立同分布于总体
1.单个正态总体
1.样本均值: X ˉ ∼ N ( μ , σ 2 n ) \bar{X}\sim N(μ,\dfrac{σ²}{n}) Xˉ∼N(μ,nσ2), X ˉ − μ σ n = ( X ˉ − μ ) n σ ∼ N ( 0 , 1 ) \dfrac{\bar{X}-μ}{\dfrac{σ}{\sqrt{n}}}=\dfrac{(\bar{X}-μ)\sqrt{n}}{σ}\sim N(0,1) nσXˉ−μ=σ(Xˉ−μ)n∼N(0,1)
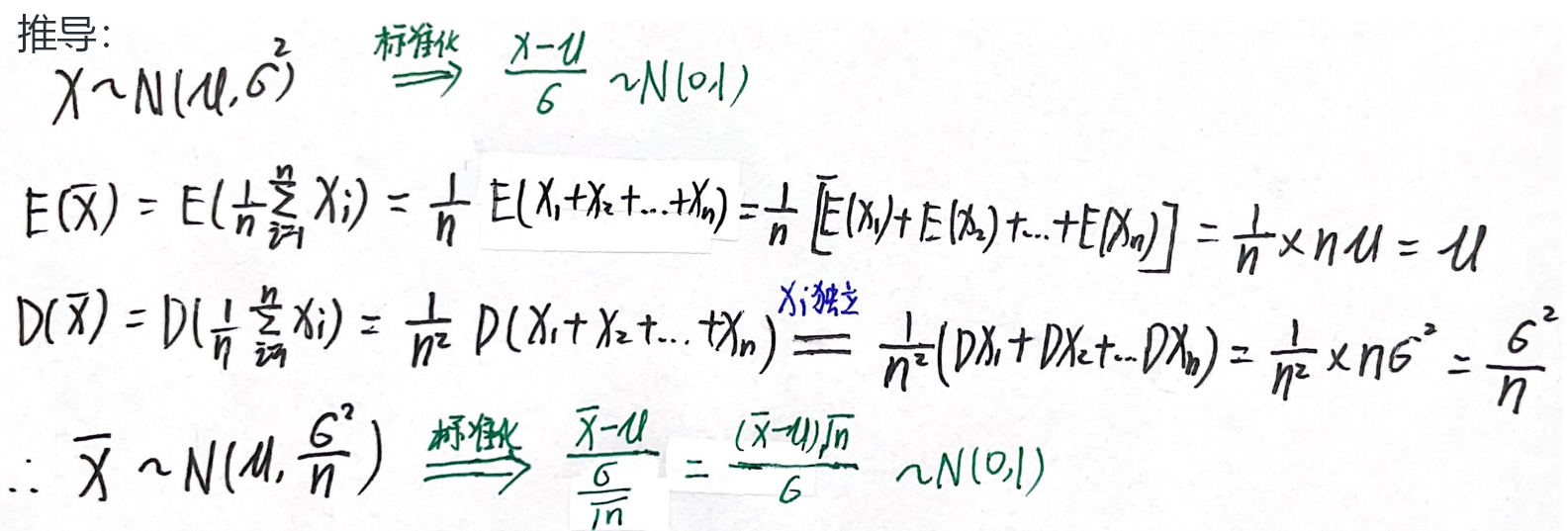
2. ∑ i = 1 n ( X i − μ σ ) 2 ∼ χ 2 ( n ) \sum\limits_{i=1}^n(\dfrac{X_i-μ}{σ})^2\sim \chi^2(n) i=1∑n(σXi−μ)2∼χ2(n)
3. ∑ i = 1 n ( X i − X ‾ σ ) 2 = \sum\limits_{i=1}^n(\dfrac{X_i-\overline{X}}{σ})^2= i=1∑n(σXi−X)2= ( n − 1 ) S 2 σ 2 ∼ χ 2 ( n − 1 ) \dfrac{(n-1)S^2}{σ^2}\sim \chi^2(n-1) σ2(n−1)S2∼χ2(n−1)
∴ E ( S 2 ) = σ 2 , D ( S 2 ) = 2 σ 4 n − 1 E(S²)=σ²,D(S²)=\dfrac{2σ^4}{n-1} E(S2)=σ2,D(S2)=n−12σ4
4. ( X ˉ − μ ) S n = n ( X ˉ − μ ) S ∼ t ( n − 1 ) \dfrac{(\bar{X}-μ)}{\dfrac{S}{\sqrt{n}}}=\dfrac{\sqrt{n}(\bar{X}-μ)}{S}\sim t(n-1) nS(Xˉ−μ)=Sn(Xˉ−μ)∼t(n−1)
∴ n ( X ˉ − μ ) 2 S 2 ∼ F ( 1 , n − 1 ) \dfrac{n(\bar{X}-μ)^2}{S^2}\sim F(1,n-1) S2n(Xˉ−μ)2∼F(1,n−1)
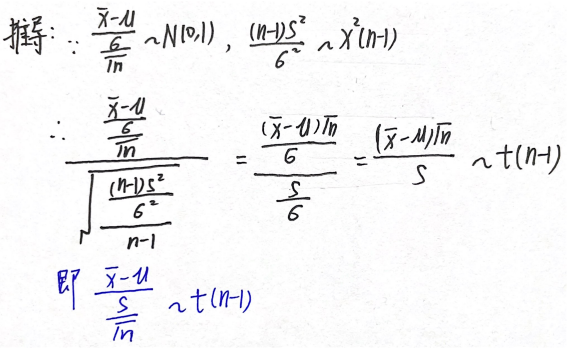
5.样本均值 X ˉ \bar{X} Xˉ与样本方差 S 2 S^2 S2相互独立,即 E ( X ˉ S ) = E ( X ˉ ) E ( S ) E(\bar{X}S)=E(\bar{X})E(S) E(XˉS)=E(Xˉ)E(S)
例题1:23李林四(四)16.
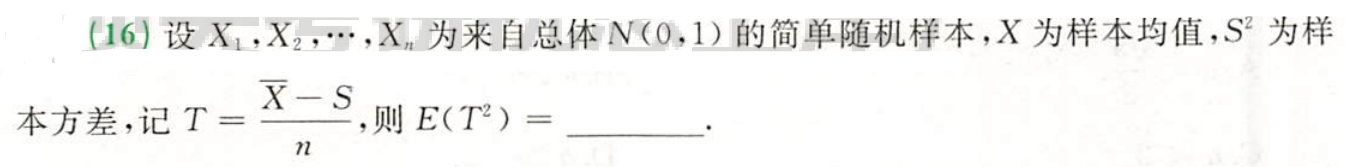
分析:样本均值 X ˉ \bar{X} Xˉ与样本方差 S 2 S^2 S2相互独立,即 E ( X ˉ S ) = E ( X ˉ ) E ( S ) E(\bar{X}S)=E(\bar{X})E(S) E(XˉS)=E(Xˉ)E(S)
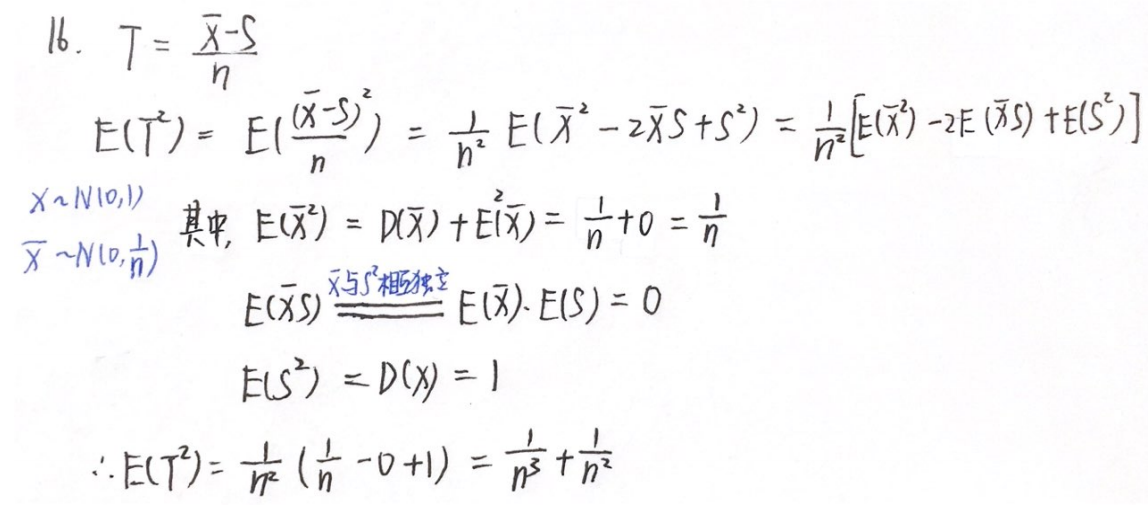
答案: 1 n 3 + 1 n 2 \dfrac{1}{n^3}+\dfrac{1}{n^2} n31+n21
例题2:05年14. 抽样分布定理、F分布

分析:由抽样分布定理得,ABC均错的很离谱。
D: X i ∼ N ( 0 , 1 ) X_i\sim N(0,1) Xi∼N(0,1),即 X i X_i Xi服从标准正态分布
X 1 2 1 ∑ i = 2 n X i 2 n − 1 ∼ F ( 1 , n − 1 ) \dfrac{\frac{X_1^2}{1}}{\frac{\sum\limits_{i=2}^nX_i^2}{n-1}}\sim F(1,n-1) n−1i=2∑nXi21X12∼F(1,n−1),D正确
答案:D
例题3:17年8. 抽样分布定理

分析:

答案:B
例题4:23李林六套卷(六)10.

分析:AB明显正确
C. ( n − 1 ) S 2 σ 2 = ∑ i = 1 n ( X i − X ˉ σ ) 2 ∼ χ 2 ( n − 1 ) \dfrac{(n-1)S^2}{σ^2}=\sum\limits_{i=1}^n(\dfrac{X_i-\bar{X}}{σ})^2\simχ^2(n-1) σ2(n−1)S2=i=1∑n(σXi−Xˉ)2∼χ2(n−1),且卡方分布具有独立可加性,∴C正确
D.应该改为2n-2
答案:D
2.两个正态总体
相关文章:

概率论与数理统计:第六章:数理统计
文章目录 Ch6. 数理统计(一) 总体与样本(二) 统计量 (5个)2.5个常用统计量3.矩的概念 (三) 抽样分布 (3个)0.上α分位点1.χ分布2.t分布3.F分布 (四) 抽样分布定理1.单个正态总体2.两个正态总体 Ch6. 数理统计 (一) 总体与样本 1.概念: (1)总体 (2)样本 简单随机…...
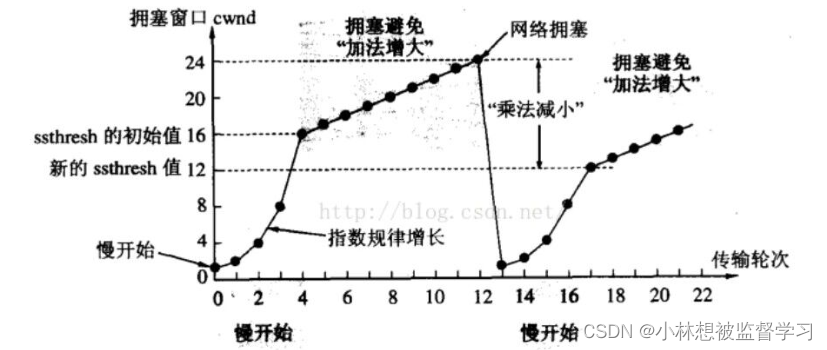
拥塞控制(TCP限制窗口大小的机制)
拥塞控制机制可以使滑动窗口在保证可靠性的前提下,提高传输效率 关于滑动窗口的属性以及部分机制推荐看TCP中窗口和滑动窗口的含义以及流量控制 拥塞控制出现的原因 看了上面推荐的博客我们已经知道了,由于接收方接收数据的能力有限,所以要通…...

校园供水系统智能管理
import pandas as pd data1pd.read_excel("C://Users//JJH//Desktop//E//附件_一季度.xlsx") data2pd.read_excel("C://Users//JJH//Desktop//E//附件_二季度.xlsx") data3pd.read_excel("C://Users//JJH//Desktop//E//附件_三季度.xlsx") data4…...

Flask-SocketIO和Flask-Login联合开发socketio权限系统
设置 Flask, Flask-SocketIO, Flask-Login: 首先,确保安装了必要的库: pip install Flask Flask-SocketIO Flask-Login基础设置: from flask import Flask, render_template, redirect, url_for, request from flask_socketio import SocketIO, emit from flask_…...

航空电子设备中的TSN通讯架构—直升机
前言 以太网正在迅速取代传统网络,成为航空电子设备和任务系统的核心高速网络。本文提出了以太网时间敏感网络(TSN)在航空电子设备上应用的技术优势问题。在实际应用中,TSN已成为一个具有丰富的机制和协议的工具箱,可满足与时间和可靠性相关…...

elment-ui中使用el-steps案例
el-steps案例 样式 代码 <div class"active-box"><div class"active-title">请完善</div><el-steps :active"active" finish-status"success" align-center><el-step title"第一步" /><…...

FPGA解析串口指令控制spi flash完成连续写、读、擦除数据
前言 最近在收拾抽屉时找到一个某宝的spi flash模块,如下图所示,我就想用能不能串口来读写flash,大致过程就是,串口向fpga发送一条指令,fpga解析出指令控制flah,这个指令协议目前就是: 55 AA …...

msvcp120.dll丢失的解决方法,分享三种快速修复的方法
今天,我将和大家分享一个关于电脑问题的解决方法——msvcp120.dll丢失的解决方法。希望对大家有所帮助。 首先,让我们来了解一下msvcp120.dll文件。msvcp120.dll是Microsoft Visual C 2010 Redistributable Package的一个组件,它包含了一些运…...
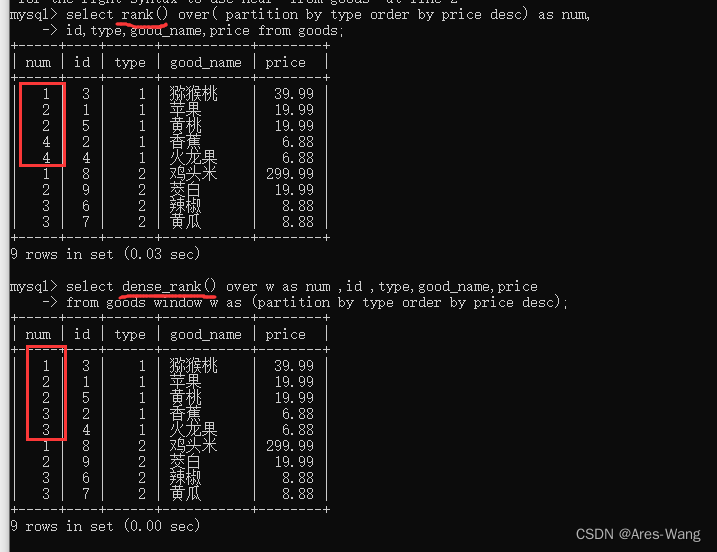
mysql 8.0 窗口函数 之 序号函数 与 sql server 序号函数 一样
sql server 序号函数 序号函数 ROW_NUMBER() 顺序排序RANK() 并列排序,会跳过重复的序号,比如序号为1,1,3DENSE_RANK() 并列排序,不会跳过重复的序号,比如 序号为 1,1,2 语法结构…...
fastgpt构建镜像
1.把client目录复制到服务器 .next和node_modules文件夹不用上传到服务器 在服务器目录运行 docker build -t fastgpt:1.0.3 . 构建服务 再运行 docker ps 就可以看到容器了...

Git笔记--分支常用命令
目录 1--git branch -v 2--git branch 3--git checkout 4--git merge 1--git branch -v git branch -v git branch -v 用于查看分支版本; 2--git branch git branch xxxxx # xxxxx表示分支名 git branch 用于创建分支; 3--git checkout git check…...

常见设计模式学习+面试总结
一 设计模式简介 二 面试总结 1 什么是单例模式?都有哪些地方用到单例? 内存中只会创建且仅创建一次对象的设计模式,保证一个类只有一个实例,并且提供一个访问该全局访问点。 应用场景: 网站的计数器,一般…...

sql解决取多个截至每个月的数据
问题:需要查询1月、1-2月、1-3月… 1-12月,分区间的累计数据,在同一个sql语句里面实现。 多个分开查询效率不高,并且数据手动合并麻烦。 with t1 as ( SELECT *,CASE WHEN insutype 390 THEN 居民 ELSE 职工 END 人员类别,SUBST…...
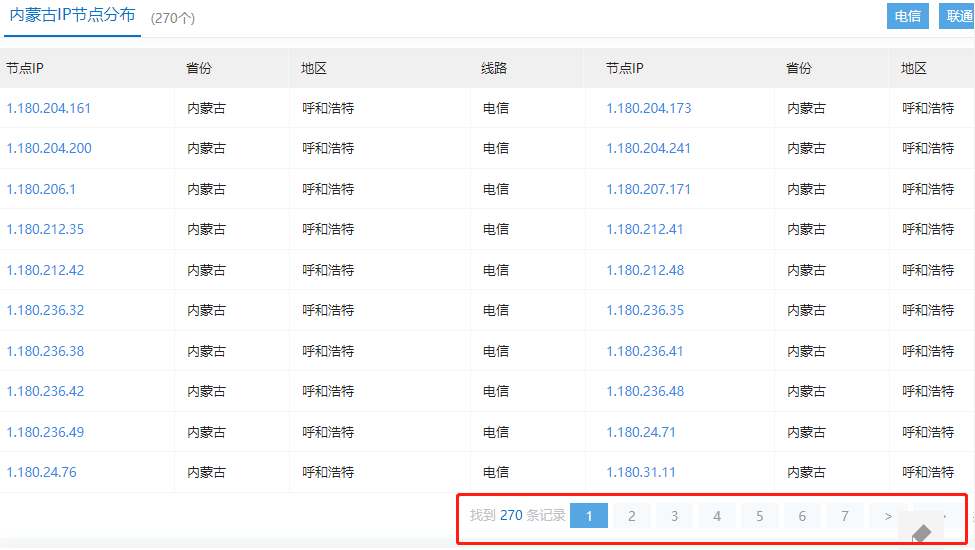
数据采集:selenium 获取 CDN 厂家各省市节点 IP
写在前面 工作需要遇到,简单整理理解不足小伙伴帮忙指正 对每个人而言,真正的职责只有一个:找到自我。然后在心中坚守其一生,全心全意,永不停息。所有其它的路都是不完整的,是人的逃避方式,是对…...
【el-tree】树形组件图标的自定义
饿了么树形组件的图标自定义 默认样式: 可以看到el-tree组件左侧自带展开与收起图标,咱们可以把它隐藏:: .groupList {::v-deep .el-tree-node { .el-icon-caret-right {display: none;} } } 我的全部代码 <div class"groupList"><el…...
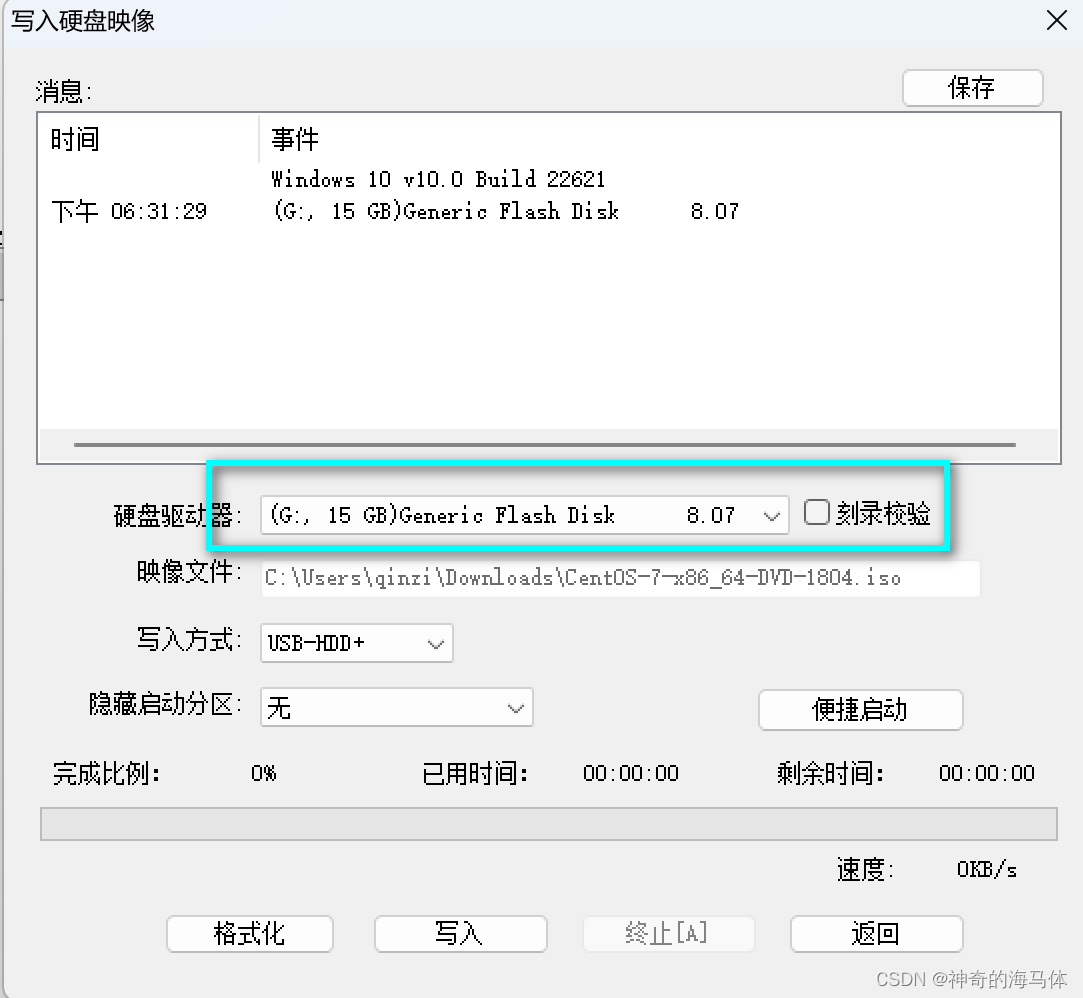
UltralSO软碟通制作Linux系统盘
第一步: 下载镜像 阿里云下载地址:https://mirrors.aliyun.com/centos-vault/ 按照需求选择系统版本,我这要求安装CentOS7.5的系统,我以CentOS7.5为例 第二步: 下载UltralSO软件 官网下载地址:https://cn.…...

yolov8训练心得 持续更新
目录 优化器 lion优化器,学习率0.0001,训练效果: 学习率衰减 600个batch衰减0.7,发现效果较好...
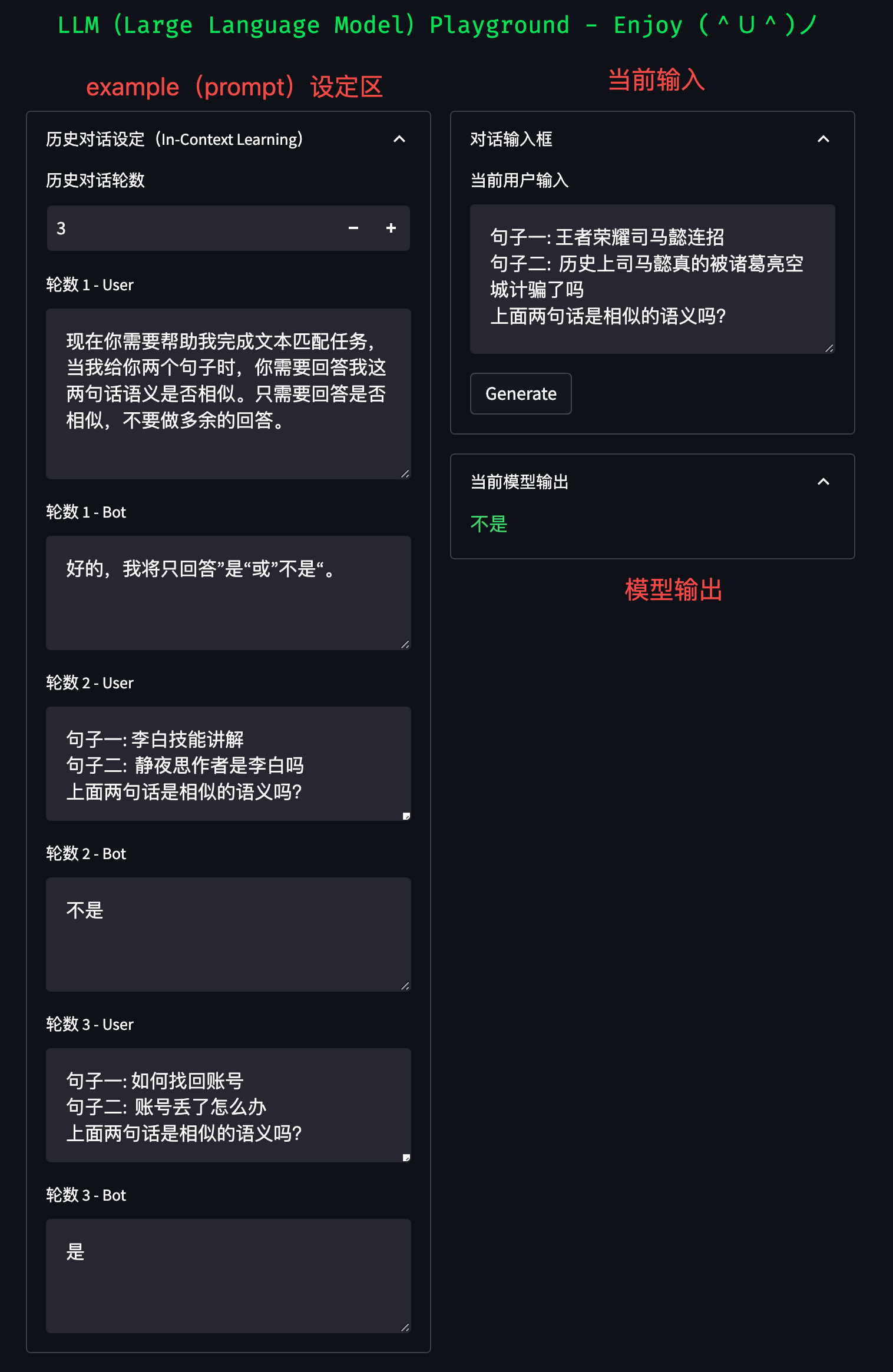
超越界限:大模型应用领域扩展,探索文本分类、文本匹配、信息抽取和性格测试等多领域应用
超越界限:大模型应用领域扩展,探索文本分类、文本匹配、信息抽取和性格测试等多领域应用 随着 ChatGPT 和 GPT-4 等强大生成模型出现,自然语言处理任务方式正在逐步发生改变。鉴于大模型强大的任务处理能力,未来我们或将不再为每…...

Compose - 基本使用
一、概念 1.1 Compose优势 由一个个可以组合的Composable函数拼成界面,方便维护和复用。布局模型不允许多次测量,提升了性能。Compose可以和View互操作(相互包含对方)。 1.2 声明式UI APP展示的数据绝大多数不是静态数据而是会…...
Unity3D Pico VR 手势识别
本文章使用的 Unity3D版本: 2021.3.6 , Pico SDK 230 ,Pico OS v.5.7.1 硬件Pico 4 Pico SDK可以去Pico官网下载SDK 导入SDK 第一步:创建Unity3D项目 第二步:导入 PICO Unity Integration SDK 选择 Windows > Package Manager。 在 Packag…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...

Docker、Wsl 打包迁移环境
电脑需要开启wsl2 可以使用wsl -v 查看当前的版本 wsl -v WSL 版本: 2.2.4.0 内核版本: 5.15.153.1-2 WSLg 版本: 1.0.61 MSRDC 版本: 1.2.5326 Direct3D 版本: 1.611.1-81528511 DXCore 版本: 10.0.2609…...