LeetCode 1769. 移动所有球到每个盒子所需的最小操作数
有 n 个盒子。给你一个长度为 n 的二进制字符串 boxes ,其中 boxes[i] 的值为 ‘0’ 表示第 i 个盒子是 空 的,而 boxes[i] 的值为 ‘1’ 表示盒子里有 一个 小球。
在一步操作中,你可以将 一个 小球从某个盒子移动到一个与之相邻的盒子中。第 i 个盒子和第 j 个盒子相邻需满足 abs(i - j) == 1 。注意,操作执行后,某些盒子中可能会存在不止一个小球。
返回一个长度为 n 的数组 answer ,其中 answer[i] 是将所有小球移动到第 i 个盒子所需的 最小 操作数。
每个 answer[i] 都需要根据盒子的 初始状态 进行计算。
示例 1:
输入:boxes = “110”
输出:[1,1,3]
解释:每个盒子对应的最小操作数如下:
- 第 1 个盒子:将一个小球从第 2 个盒子移动到第 1 个盒子,需要 1 步操作。
- 第 2 个盒子:将一个小球从第 1 个盒子移动到第 2 个盒子,需要 1 步操作。
- 第 3 个盒子:将一个小球从第 1 个盒子移动到第 3 个盒子,需要 2 步操作。将一个小球从第 2 个盒子移动到第 3 个盒子,需要 1 步操作。共计 3 步操作。
n == boxes.length
1 <= n <= 2000
boxes[i] 为 ‘0’ 或 ‘1’
解法一:直接模拟:
class Solution {
public:vector<int> minOperations(string boxes) {int boxNum = boxes.size();vector<int> ans(boxNum);for (int i = 0; i < boxNum; ++i) {for (int j = 0; j < boxNum; ++j) {if (boxes[j] == '1') {ans[i] += abs(j - i);}}}return ans;}
};
如果有n个盒子,此算法时间复杂度为O(n2^22),空间复杂度为O(1)。
解法二:如果我们知道第i个盒子需要操作x次,且第i个盒子左边有n个球,右边有m个球,如果第i个盒子里没有球,则第i+1个盒子需要操作x+left-right次,因为左边的球多移动一次,右边的球少移动一次;如果第i个盒子里有球,则第i+1个盒子需要操作x+left+1-right+1次,因为不仅左边的球要多移动一次,第i个球也要移动一次,不仅右边的球少移动一次,右边的球的数量还少了一个:
class Solution {
public:vector<int> minOperations(string boxes) {int boxNum = boxes.size();vector<int> ans(boxNum);int left = 0, right = 0;if (boxes[0] == '1') {left = 1;}for (int i = 1; i < boxNum; ++i) {if (boxes[i] == '1') {ans[0] += i;++right;}}for (int i = 1; i < boxNum; ++i) {ans[i] += ans[i - 1] + left - right;if (boxes[i] == '1') {--right;++left;}}return ans;}
};
此算法时间复杂度为O(n),空间复杂度为O(1)。
相关文章:

LeetCode 1769. 移动所有球到每个盒子所需的最小操作数
有 n 个盒子。给你一个长度为 n 的二进制字符串 boxes ,其中 boxes[i] 的值为 ‘0’ 表示第 i 个盒子是 空 的,而 boxes[i] 的值为 ‘1’ 表示盒子里有 一个 小球。 在一步操作中,你可以将 一个 小球从某个盒子移动到一个与之相邻的盒子中。…...
配置简要笔记)
MKS SKIPR V1.0船长版(Voron 2.4 R2)配置简要笔记
第一次用MKS SKIPR V1.0,设置过程中,也不知道怎么回事,跟现有的资料有些出入。首先,基本的配置调试可以参考官方的使用说明。 MKS SKIPR V1.0 使用说明书 这个说明比较简单,很多深一点的东西没有提现,不过…...
90后,转行软件测试3年,从月入7000+到月入过万,整理出的这一万字经验分享。
周一发工资了,到手12857.65,美滋滋 今年是我毕业参加工作的第3年,工资终于来到5位数了。上一家公司月薪7000,实际拿到手就6450左右,感觉今年真的是元气满满啊,工资翻倍,良好的人生开端。 想起…...
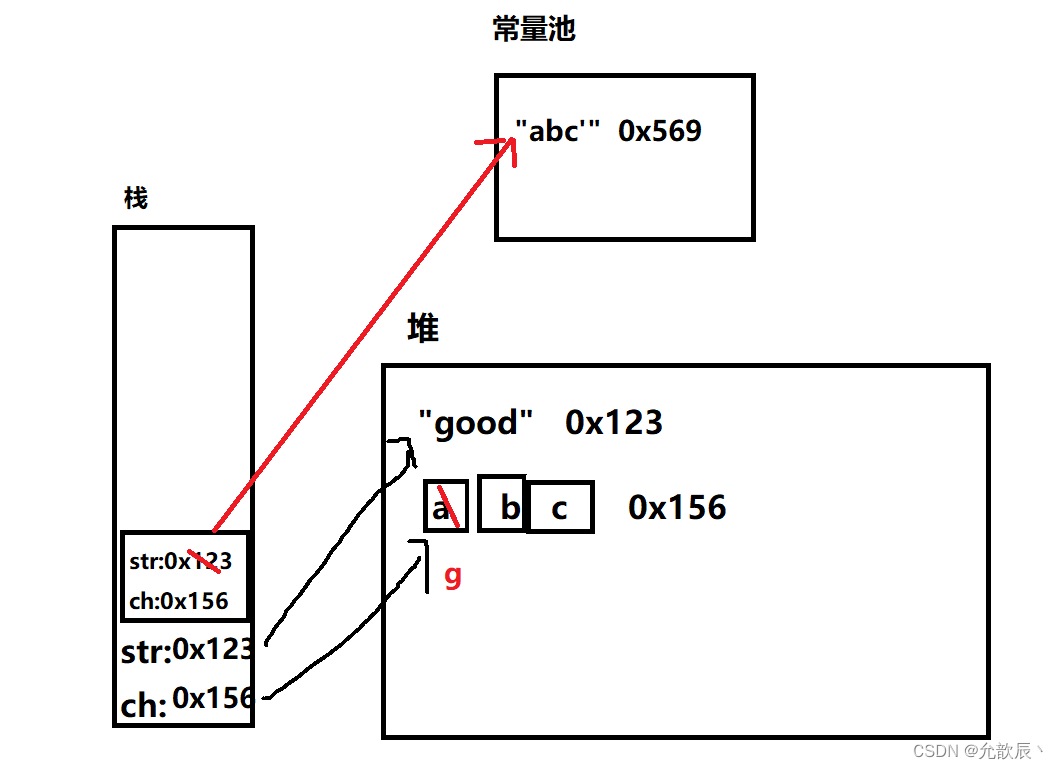
Java之关于String字符串笔试面试重点
目录 一.关于字符串的常量池 1.关于字符串产生的三种方式 2.关于字符串的常量池 3.直接赋值法和new的方式产生对象的区别 二.关于intern方法 1.情况一(已经包含) 2.情况二(已经包含) 3.情况三(未包含) 4.情况四 三.关于字符串的不可变性 1.了解字符串的不可变性 2.Str…...
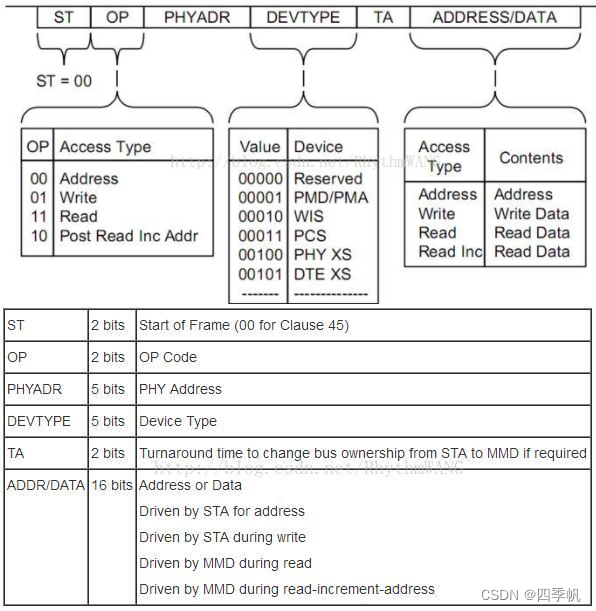
mdio协议
1. 简介 MDIO接口中有特定的术语定义总线上的各种设备,驱动MDIO总线的设备被定义为站管理实体(STA),而被MDC管理的目标设备称为可被MDIO管理的设备(MMD)。 STA初始化MDIO所有的通信,同时负责驱动…...

kubectl命令
kubectl命令是操作 Kubernetes 集群的最直接和最高效的途径。 1、kubectl自动补全 $ source <(kubectl completion bash) # setup autocomplete in bash, bash-completion package should be installed first. $ source <(kubectl completion zsh) # setup autocomple…...

题库-JAVASE01
文章目录1.JAVA开发环境2.JAVA变量3.JAVA基本类型4.运算符和表达式5.分支结构6.循环结构7.数组8.方法1.JAVA开发环境 (单选题)在Java中,以下描述错误的是( ) A…class是源文件 B…java是编译前的源文件 C…class是编译后的文件 D.Java程序需…...
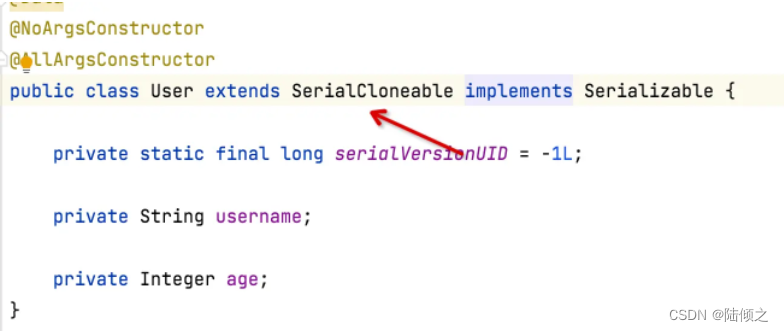
Java序列化机制
Java序列化机制 概述 java中的序列化可能都停留在实现Serializable接口上,对于它里面的一些核心机制没有深入了解过。直到最近在项目中踩了一个坑,就是序列化对象添加一个字段以后,使用方系统报了反序列化失败,原因是我们双方的…...
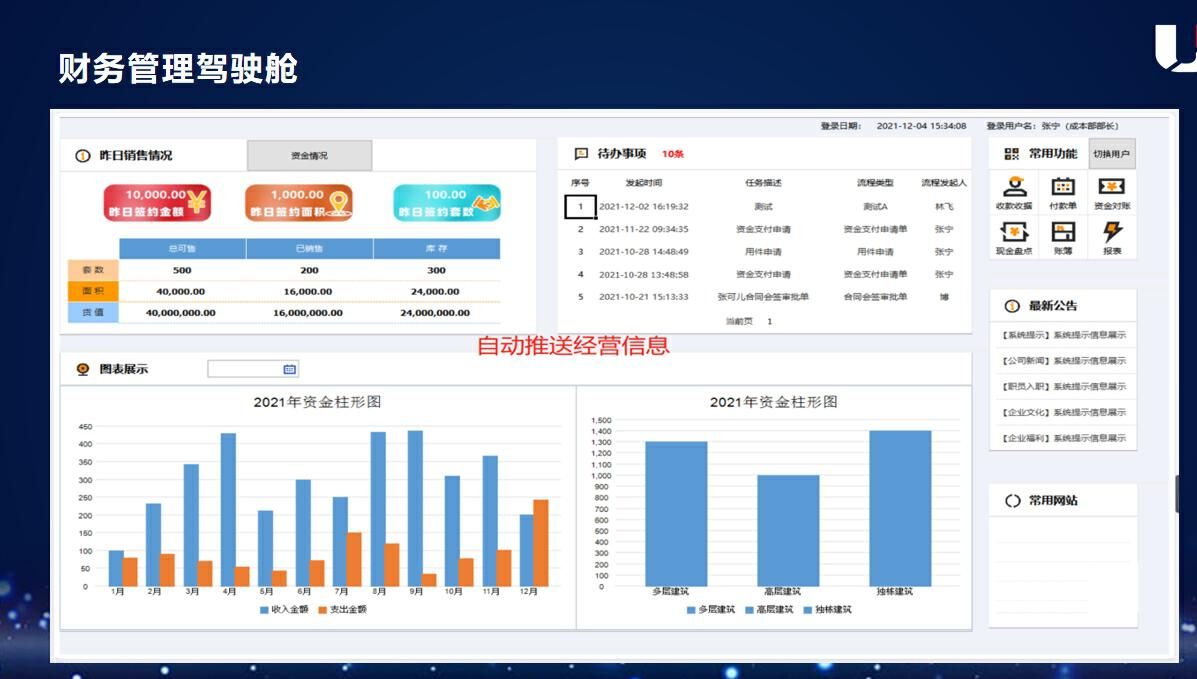
3款强大到离谱电脑软件,都是效率神器,从此远离加班
闲话少说,直接上狠货。 1、ImageGlass ImageGlass是一款值得吹爆的电脑图片浏览工具,使用极其方便,体积50M左右,非常小巧,功能却强大到离谱,ImageGlass打开图片的速度极快,实现快速不同图像间切…...
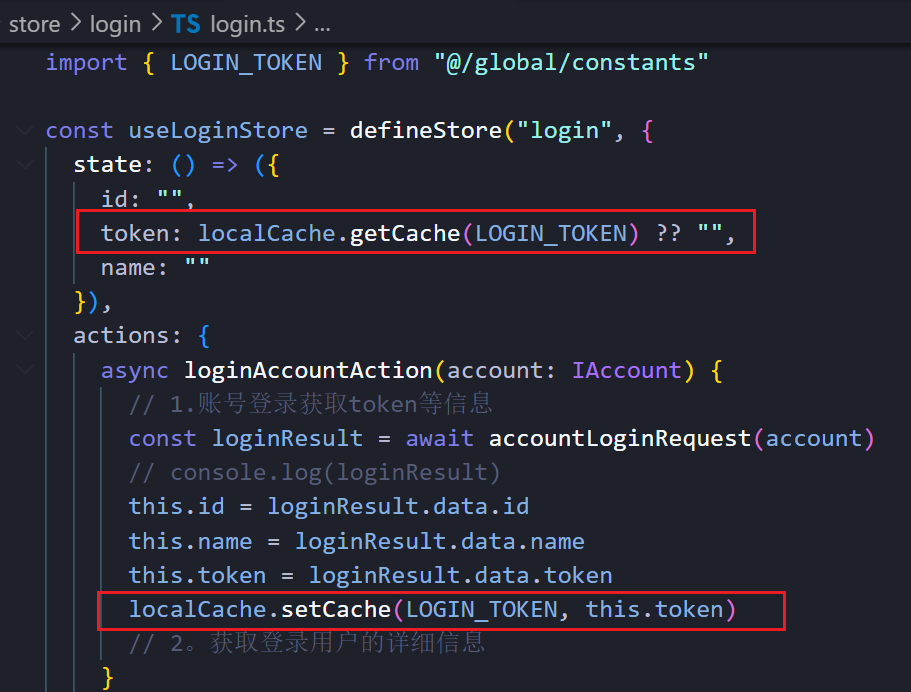
【项目】Vue3+TS CMS 登录模块搭建
💭💭 ✨:Vue3 TS 💟:东非不开森的主页 💜: keep going💜💜 🌸: 如有错误或不足之处,希望可以指正,非常感谢😉 Vue3TS一、…...

Java 8 的那些常见写法
前言 现在Java已经发展到Java19版本了,由于Java后面一些版本,就开始商用收费了,所以目前绝大多数公司的JDK版本都是采用的之前稳定且免费的1.8版本,也就是Java8,这个版本已经能满足几乎所有业务的需求开发了ÿ…...
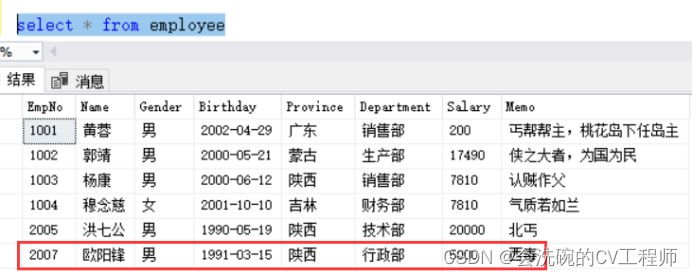
PyQt5数据库开发1 4.3 QSqlTableModel 之 相关槽函数的实现(多图长文详解)
目录 一、打开数据库表 1. 写打开数据库的槽函数 2. 运行后发现数据库可以打开了 3. ODBC配通了,数据库还是打不开 4. 写在tableView上显示数据库表的函数 5. 运行后发现表可以显示了 6. 代码分析 7. 添加列名称 8. 根据内容调整列宽 9. 备注:…...
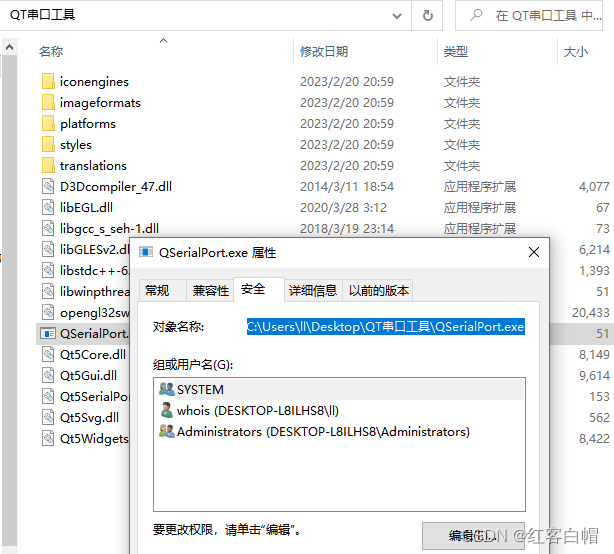
QT 设计一个串口调试工具,用一个工程就能轻松解决,外加虚拟串口工具模拟调试,在日常工作中可类比模块间通信,非常详细建议收藏
QT 串口调试工具第一节 虚拟串口工具安装第二节 QT创建一个基于QWidget的项目第三节 UI界面设计第三节 项目头文件widget.h第四节 项目实现文件widget.cpp第五节 main函数第六节 编译结果重点第七节 使用QT打包程序,不安装QT的电脑可使用第一节 虚拟串口工具安装 -…...
OpenSumi 是信创开发云的首选
原文作者:行云创新技术总监 邓冰寒 引言 随着云原生应用的日益普及,开发上云也逐步被越来越多的厂商和开发者接受,在这个赛道国内外有不少玩家,国外的 GitHub Codespaces、CodeSandbox,GitPod、亚马逊 Cloud9…...

JdbcTemplate常用方法解析
文章目录1.JdbcTemplate简介2.JdbcTemplate主要方法:3.常用方法介绍update()方法增删改query()查询方法1.JdbcTemplate简介 JdbcTemplate是Spring JDBC的核心类,借助该类提供的方法可以很方便的实现数据的增删改查。 Spring对数据库的操作在jdbc上面做…...
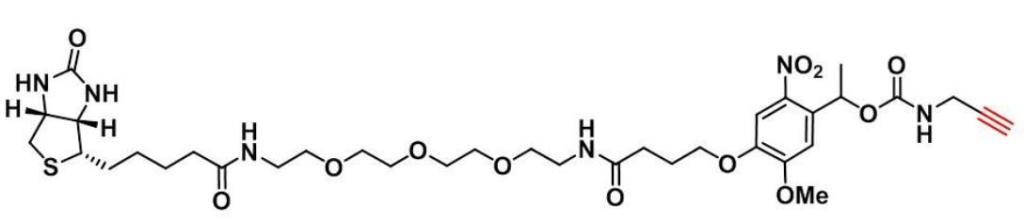
生物素标记试剂1869922-24-6,Alkyne-PEG3-Biotin PC,炔烃PEG3生物素PC
1、试剂基团反应特点(Reagent group reaction characteristics):PC alkyne-PEG3-Biotin含一个炔烃和一个 PEG 链接的可光裂解生物素基团。含 3 个单元 PEG 的 ADC linker,生物素本身是个游离的小分子,在生物实验中常常…...

CS224W课程学习笔记(三):DeepWalk算法原理与说明
引言 什么是图嵌入? 图嵌入(Graph Embedding,也叫Network Embedding) 是一种将图数据(通常为高维稠密的矩阵)映射为低微稠密向量的过程,能够很好地解决图数据难以高效输入机器学习算法的问题。…...

rk3568 开发板Ubuntu系统说明
Ubuntu MinimalUbuntu Minimal系统基于Ubuntu 64bit系统构建,目前发布有Ubuntu18.04这个版本。与Ubuntu Desktop 相比具有以下特性:没有桌面环境,占用资源少,在简化网络管理之后,只需40M内存;针对嵌入式平台…...

Windows和Linux常用HASH算法使用命令
Windows和Linux常用hash算法使用命令 Windows,以文件xxx.zip为例 Windows 求文件 md5 certutil -hashfile xxx.zip md5Windows 求文件 sha1 certutil -hashfile xxx.zip sha1Windows 求文件 sha256 certutil -hashfile xxx.zip sha256Linux,以文件xxx.z…...
货仓选址 AcWing(JAVA)
在一条数轴上有 N家商店,它们的坐标分别为 A1∼AN。 现在需要在数轴上建立一家货仓,每天清晨,从货仓到每家商店都要运送商品。 为了提高效率,求把货仓建在何处,可以使得货仓到每家商店的距离之和最小。 输入格式&#…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...
