C++动态规划经典案例解析之合并石子
1. 前言
区间类型问题,指求一个数列中某一段区间的值,包括求和、最值等简单或复杂问题。此类问题也适用于动态规划思想。
如前缀和就是极简单的区间问题。如有如下数组:
int nums[]={3,1,7,9,12,78,32,5,10,11,21,32,45,22}
现给定区间信息[3,6],求区间内所有数字相加结果。即求如下图位置数字之和。
Tips: 区间至少包括
2个属性,起始端和结束端,求和范围包含左端和右端数字。

直接的解法:
- 累加数组中
0~6区间的值s1。 - 累加数组中
0~2区间的值s2。 - 将
s1中的值减去s2中的值。得到最终结果。
如果对任意区间的求解要求较频繁,会存在大量的重复计算。如分别求区间[2,5]和[1,5]之和时,分析可知区间[1,5]结果等于区间[2,5]的结果加上nums[1]的值,或者说区间[2,5]的值等于[1,5]的值减nums[1]。简而言之,只需要求出一个如上两个区间中一个区间的值,另一个区间的值就可得到。
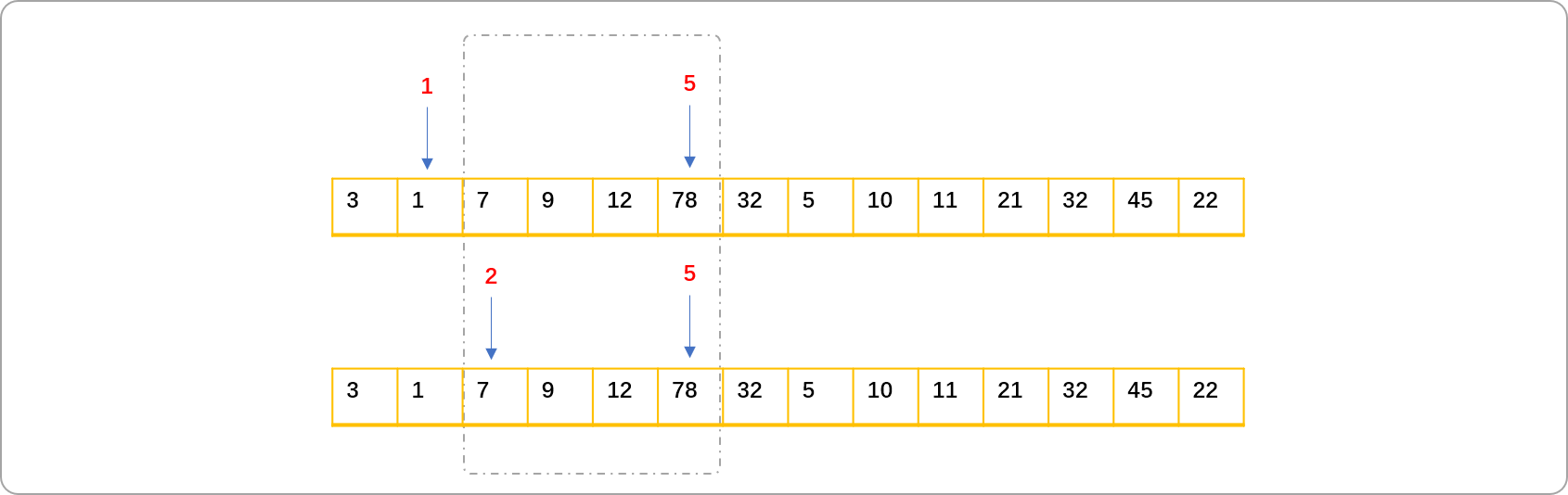
为了减少重复计算,可使用区间缓存理念记录0~至任意位置的和。
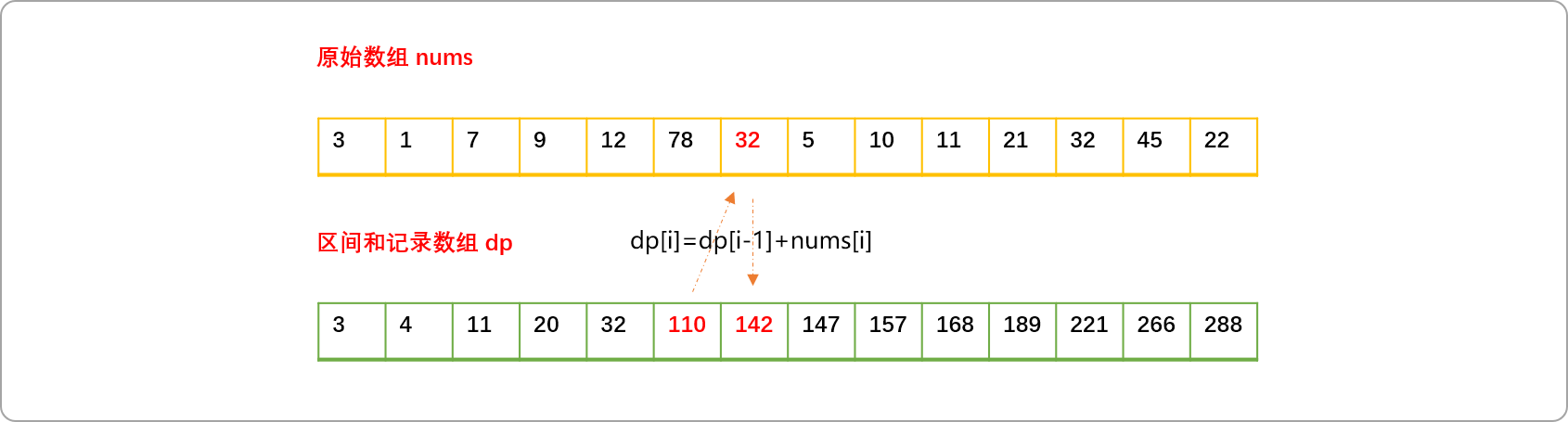
如上的问题便是简单的区间类型问题,解决此类问题的方案称为简单区间类型动态规划。dp数组也可称为前缀和数组。
编码实现:
#include <iostream>
using namespace std;
int main() {int nums[]= {3,1,7,9,12,78,32,5,10,11,21,32,45,22};int dp[100];int size=sizeof(nums)/sizeof(int);for(int i=0; i<size; i++) {if(i==0){//base case dp[i]=nums[i];}else{dp[i]=dp[i-1]+nums[i];}}//输出dp信息for(int i=0; i<size; i++) {cout<<dp[i]<<"\t";}return 0;
}
有了前缀和数组,计算任意区间数字和的公式为:
//[l,r]:l表示左端位置,r表示右端位置
dp[r]-dp[l-1];
如下代码实现,输入任意区间信息,输出区间和信息。
#include <iostream>
using namespace std;
int main() {int nums[]= {3,1,7,9,12,78,32,5,10,11,21,32,45,22};int dp[100];int size=sizeof(nums)/sizeof(int);for(int i=0; i<size; i++) {if(i==0) {//base casedp[i]=nums[i];} else {dp[i]=dp[i-1]+nums[i];}}//输出dp信息for(int i=0; i<size; i++) {cout<<dp[i]<<"\t";}cout<<endl;int l,r,sum;while(1) {cin>>l>>r;if(l==-1)break;sum=dp[r]-dp[l-1];cout<<sum<<endl;}return 0;
}
前缀和是区间动态规划的极简单应用,下文继续讲解几道典型的区间类型问题。
2. 典型案例
2.1 石子合并
问题描述:
设有N(N<=300)堆石子排成一排,其编号为1,2,3...N,每堆石子有一定的质量m[i] (m[i]<=1000)。现在要将这N堆石子合并成为一堆,每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子相邻的石子将和新堆相邻。合并时由于选择的顺序不同,合并的总代价也不相同。试找出一种合理的方法,使总的代价最小,并输出最小代价。
此问题为什么也是区间类型问题?
先看几个样例。如有编号为 1,2,3 的 3 堆石子,质量分别为 1,2,3。则合并方案有如下 2 种:
- 合并编号为
1、2的石子,合并代价为3,再合并新堆和第3堆石子,代价为6。总代价为9。 - 合并编号为
2、3的石子,合并代价为5,再合并新堆和第1堆石子,代价为6。总代价为11。
通过上述合并过程,可得到如下有用的结论:
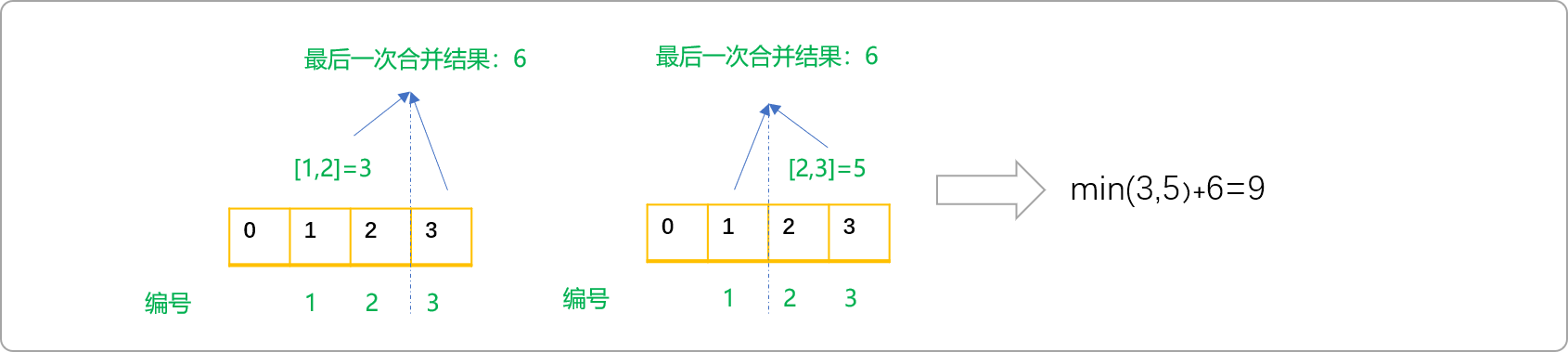
- 任意相邻两堆石子合并的结果是以这两堆石子的编号作为左、右边界的区间和。如合并编号
1,2的石子,代价为区间[1,2]的和 。合并编号为2、3的石子,结果为区间[2,3]的和。

-
无论采用何种合并方案,最后一次合并都是相当于求整个数列的和。
如样例所示,两种合并方案的代价分别为
3,5,取最小值3再加上所有石子的质量和6,即为最后答案9。
-
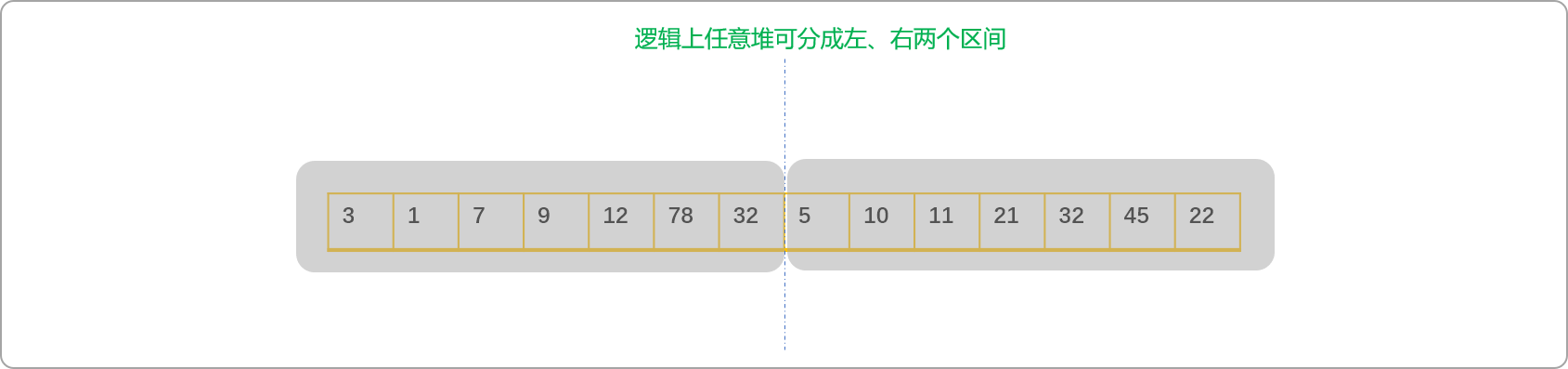
对于
n堆的石子,可以随意在中间画出一条分割线,把n堆石子抽象成左、右2堆石子(两个区间),根据上述分析,可知最后一次的合并值为这2堆石子的质量总和。但是,左堆不是真正意义上只有一堆石子,是由许多石子堆组成的一个逻辑整体,有其内部的合并方案,且不止一种,站在宏观的角度,不用关心其内部如何变化,只需关心多种合并方案的最小值是多少。同理,也只需关心右堆最终返回的最佳值。
所以,求解问题可以抽象成:
最终合并最小值=所有石子堆的总质量值+左堆最小合并值+右堆最小合并值
如果原始问题是一个根问题,则求解左堆或右堆的最佳合并值就是一个子问题,所以,合并石子这道题本质是符合递归特点的。
既然符合递归特点,现在就要考虑如何划分子问题。
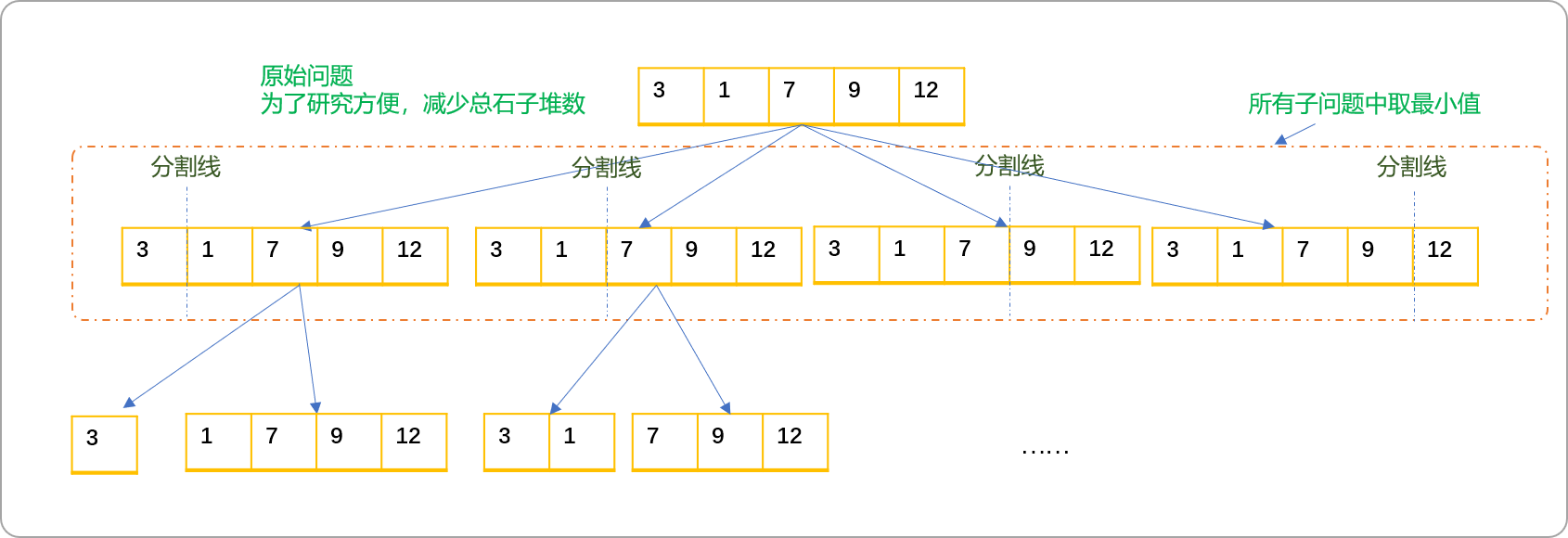
绘制如下图递归树,根问题为原始问题,区间划分可以从第一堆石子开始,然后再移动分割线,最后再在多个子问题返回值中取最小值。
Tips: 如果只有一堆石子,则代价为
0。
编码实现:
- 初如化变量。
#include <iostream>
#include <cmath>
using namespace std;
//石子质量
int sz[100]={0};
//石子堆数量
int n;
//前缀和
int s[100]={0};
- 初始化石子信息和前缀和。
/*
* 初始化
*/
void init(){cin>>n;for(int i=1;i<=n;i++){cin>>sz[i];}//动态规划计算前缀和for(int i=1;i<=n;i++){s[i]=s[i-1]+sz[i];}
}
- 递归实现,子问题是一个区间问题,由左、右分界线确定。
int getSz(int l,int r) {//只有一堆石子,返回 0if(l==r)return 0;int res=1<<30;//得到区间的和,最后一次合并值int sum=s[r]-s[l-1];//计算可分方案,且返回所有分割方案中的最小值for(int k=l; k<r; k++) {res=min(res, getSz(l,k) + getSz(k+1,r) );}//返回最后一次合并的值加上左、右区间的合并值return sum+res;
}
- 测试。
int main() {init();int res= getSz(1,n);cout<<res;return 0;
}
是否存在重叠子问题?
如下图所示,当石子堆更多时,重叠子问题更多。
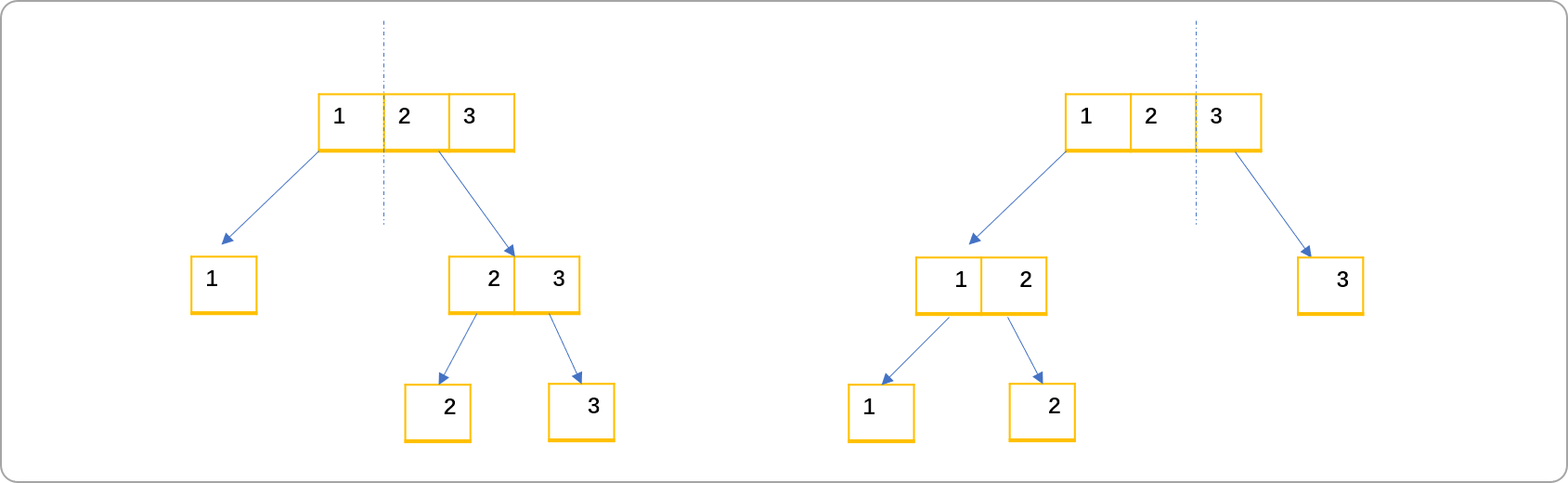
使用记忆搜索解决重叠子问题。
//记忆数组
int dp[100][100]={0};
int getSz(int l,int r) {//只有一堆石子,返回 0if(l==r)return 0;if(dp[l][r]!=0)return dp[l][r];int res=1<<30;//得到区间的和,最后一次合并值int sum=s[r]-s[l-1];//计算可分方案,且返回所有分割方案中的最小值for(int k=l; k<r; k++) {res=min(res, getSz(l,k) + getSz(k+1,r) );}return dp[l][r]=sum+res;
}
递归是由上向下逐步向子问题求助,类似问题也可以采用由下向上的动态规划方案实现。基本思路,每一次合并过程,先两两合并,再三三合并,…最后N堆合并。
/*
*动态规划
*/
int dpSz() {int ans=0;//初始化dp 数组for (int i = 1; i <= n; i++) {for(int j=1; j<=n; j++) {dp[i][j]=1<<30;}//一堆石子的值为 0dp[i][i] = 0;}//从长度为 1 的区间开始扫描,逐步增加区间的长度for (int len = 1; len < n; len++)//左边界for (int i = 1; i < n; i++) {//右边界int j = i + len;//左右之间的所有子区间for (int k = i; k < j; k++) {dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + s[j] - s[i - 1]);}ans=max(ans,dp[i][j]);}return ans;
}
测试:
int main() {init();int res=dpSz();cout<<"动态规划方案:"<<res<<endl;printf("%d\n", dp[1][n]);return 0;
}
2.2 石子合并 II
问题描述:
有 n 堆石子围成一个圈,第 i 堆石子有 a[i] 颗,每次我们可以选择相邻的两堆石子合并,代价是两堆石子数目的和,现在我们要一直合并这些石子,使得最后只剩下一堆石子,问总代价最少是多少?
因为首尾可合并,相比较上述问题,差异在于增加合并的方案。
那么,到底增加了那些合并?
假设石子有 3 堆,每堆的质量分别为 1 2 3。
如果考虑环形问题,则任何数字都可以为头、为尾,则会出现如下几种数列。
-
1 2 3 -
2 3 1 -
3 1 2

可以理解,数列变成如下 形式,即将环形变成线性。

动态规划实现:
#include <bits/stdc++.h>
using namespace std;int n, a[501], f[501][501], s[501];int main() {scanf("%d", &n);for (int i = 1; i <= n; i++) {scanf("%d", &a[i]);a[n + i] = a[i];} for (int i = 1; i <= 2 * n; i++)s[i] = s[i - 1] + a[i];memset(f, 127, sizeof(f));for (int i = 1; i <= 2 * n; i++)f[i][i] = 0;for (int l = 1; l < 2 *n; l++)for (int i = 1; i <= 2 * n - l; i++) {int j = i + l;for (int k = i; k < j; k++)f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j] + s[j] - s[i - 1]);}int ans = 1 << 30;for (int i = 1; i <= n; i++)ans = min(ans, f[i][i + n - 1]);printf("%d\n", ans);
}
3. 总结
沉淀过程是一种修行。
相关文章:

C++动态规划经典案例解析之合并石子
1. 前言 区间类型问题,指求一个数列中某一段区间的值,包括求和、最值等简单或复杂问题。此类问题也适用于动态规划思想。 如前缀和就是极简单的区间问题。如有如下数组: int nums[]{3,1,7,9,12,78,32,5,10,11,21,32,45,22}现给定区间信息[…...

go MongoDB
安装 go get go.mongodb.org/mongo-driver/mongo package mongodbexampleimport ("context""fmt""ginapi/structs""time""go.mongodb.org/mongo-driver/bson""go.mongodb.org/mongo-driver/bson/primitive""…...
--优先队列)
算法与数据结构(八)--优先队列
普通的队列是一种先进先出的数据结构,元素在队列尾追加,而从队列头删除,在某些情况下,我们可能需要找出队列中的最大值或者最小值。 例如使用一个队列保存计算机的任务,一般情况下计算机的任务都是有优先级的ÿ…...

React 全栈体系(三)
第二章 React面向组件编程 四、组件三大核心属性3: refs与事件处理 1. 效果 需求: 自定义组件, 功能说明如下: 点击按钮, 提示第一个输入框中的值当第2个输入框失去焦点时, 提示这个输入框中的值 2. 理解 组件内的标签可以定义ref属性来标识自己 3. 编码 3.1 字符串形式…...

腾讯云下一代CDN -- EdgeOne加速MinIO对象存储
省流 使用MinIO作为EdgeOne的源站。 背景介绍 项目中需要一个兼容S3协议的对象存储服务,腾讯云的COS虽然也兼容S3协议,但是也只是支持简单的上传下载,对于上传的时候同时打标签这种需求,就不兼容S3了。所以决定自建一个对象存储…...

GitLab-CI 指南
GitLab CI 指南 前置工作 部署GitLab 部署GitLab-Runner 注册Runner到GitLab docker exec -it gitlab-runner bash # 进入容器 gitlab-runner register #调用register命令开始注册 # 在Gitlab Setting中找到Runners,如下图所示Enter the GitLab instance URL (for example, …...
MyBatis的核心技术掌握,简单易懂(上)
目录 一.MyBatis中的动态SQL 二.MyBatis中的模糊查询 1. # 符号 2. $ 符号 ---问题 ---所以大家知道 # 和 $ 在MyBatis中的模糊查询中的区别了嘛?? 三.MyBatis 中的结果映射 1. resultType: 2. resultMap: ---问题 ---…...

Redisson自定义序列化
Redisson自定义序列化_redisson 序列化_yzh_1346983557的博客-CSDN博客 redis存取的数据一定是可序列化的,而可序列化方式可以自定义。如果不同客户端设置的可序列化方式不一样,会导致读取不一致的问题。常见的序列化方式有几下几种...
MongoDB Long 类型 shell 查询
场景 1、某数据ID为Long类型,JAVA 定义实体类 Id Long id 2、查询数据库,此数据存在 3、使用 shell 查询,查不到数据 4、JAVA代码查询Query.query 不受任何影响 分析 尝试解决(一) long 在 mongo中为 int64 类型…...
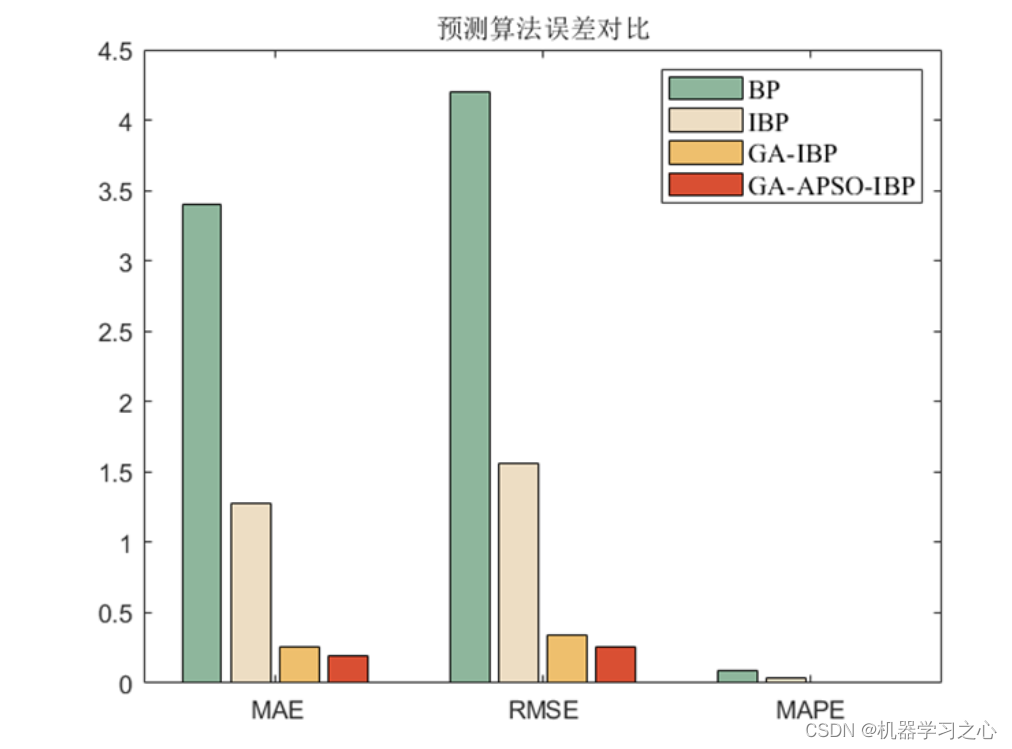
回归预测 | MATLAB实现GA-APSO-IBP改进遗传-粒子群算法优化双层BP神经网络多输入单输出回归预测
回归预测 | MATLAB实现GA-APSO-IBP改进遗传-粒子群算法优化双层BP神经网络多输入单输出回归预测 目录 回归预测 | MATLAB实现GA-APSO-IBP改进遗传-粒子群算法优化双层BP神经网络多输入单输出回归预测效果一览基本介绍模型描述程序设计参考资料 效果一览 基本介绍 MATLAB实现GA-…...

Spring cache整合Redis使用介绍
🍓 简介:java系列技术分享(👉持续更新中…🔥) 🍓 初衷:一起学习、一起进步、坚持不懈 🍓 如果文章内容有误与您的想法不一致,欢迎大家在评论区指正🙏 🍓 希望这篇文章对你有所帮助,欢…...

Metasploit提权
一、bypassuac 用户账户控制(User Account Control,简写作UAC)是微软公司在其Windows Vista及更高版本操作系统中采用的一种控制机制。其原理是通知用户是否对应用程序使用硬盘驱动器和系统文件授权,以达到帮助阻止恶意程序(有时也…...

TypeScript三种特殊类型
1.any类型 说明:any类型代表着可以赋值任意类型 let nickname:any"王二"nickname15nicknametruenicknameundefinednicknamenullnickname{}2.unknown类型 说明:类似any类型;只是不能赋值到其它类型上;除了any和known。…...

如何使用CSS实现一个响应式轮播图?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 使用CSS实现响应式轮播图的示例⭐ HTML 结构⭐ CSS 样式 (styles.css)⭐ JavaScript 代码 (script.js)⭐ 实现说明⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带…...
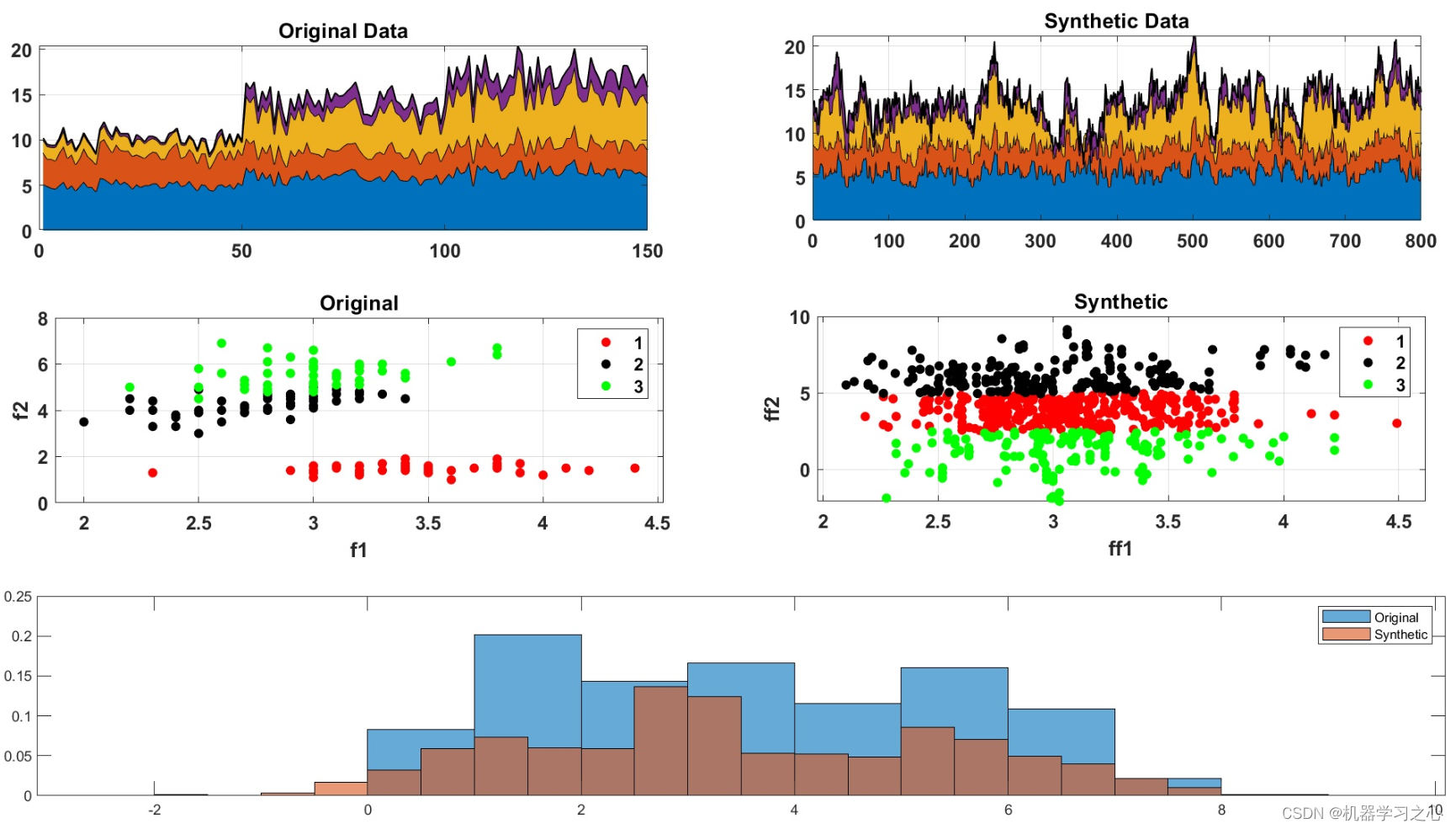
数据生成 | MATLAB实现MCMC马尔科夫蒙特卡洛模拟的数据生成
数据生成 | MATLAB实现MCMC马尔科夫蒙特卡洛模拟的数据生成 目录 数据生成 | MATLAB实现MCMC马尔科夫蒙特卡洛模拟的数据生成生成效果基本描述模型描述程序设计参考资料 生成效果 基本描述 1.MATLAB实现MCMC马尔科夫蒙特卡洛模拟的数据生成; 2.马尔科夫链蒙特卡洛方…...

【从零开始的rust web开发之路 二】axum中间件和共享状态使用
系列文章目录 第一章 axum学习使用 第二章 axum中间件使用 文章目录 系列文章目录前言一、中间件是什么二、中间件使用常用中间件使用中间件使用TraceLayer中间件实现请求日志打印自定义中间件 共享状态 前言 上篇文件讲了路由和参数相应相关的。axum还有个关键的地方是中间件…...

Vue操作时间
一、获取现在时间 const currentTime () > {let date new Date();let year date.getFullYear(); //月份从0~11,所以加一let month date.getMonth();let dateArr [date.getMonth() 1,date.getDate(),date.getHours(),date.getMinutes(),date.getSeconds(),…...

数据库——Redis 常见数据结构以及使用场景分析
文章目录 1. string2. list3. hash4. set5. sorted set 你可以自己本机安装 redis 或者通过 redis 官网提供的在线 redis 环境。 1. string 介绍 :string 数据结构是简单的 key-value 类型。虽然 Redis 是用 C 语言写的,但是 Redis 并没有使用 C 的字符串…...

数学建模-规划工具箱yalmip
官网下载 实例 %% yalmip 求解 yalmip clc;clear;close all; %% %sdpvar实型变量 intvar 整形变量 binvar 0-1型变量 psdpvar(3,1); %定义变量 %目标函数 要把求最大值转化为最小值 Objective-p(1)^2p(2)^2-p(2)*p(3);%约束条件 Constraints[0<p<1,(p(1)^2p…...

[SQL挖掘机] - 窗口函数 - 计算移动平均
介绍: 在窗口函数使用时,计算的是累积到当前行的所有的数据的相关操作。 实际上,还可以指定更加详细的汇总范围。该汇总范围称为 框架 (frame)。 其实这里也可以理解成一个窗口, 这个窗口是我们可以进行设置的. 之前我们介绍的窗口函数是根据partition…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
