LeetCode 面试题 01.09. 字符串轮转
文章目录
- 一、题目
- 二、C# 题解
一、题目
字符串轮转。给定两个字符串 s1 和 s2,请编写代码检查 s2 是否为 s1 旋转而成(比如,waterbottle 是 erbottlewat 旋转后的字符串)。
点击此处跳转题目。
示例1:
输入:s1 = “waterbottle”, s2 = “erbottlewat”
输出:True
示例2:
输入:s1 = “aa”, s2 = “aba”
输出:False
提示:
- 字符串长度在[0, 100000]范围内。
说明:
- 你能只调用一次检查子串的方法吗?
二、C# 题解
可以将题目理解为从字符串内部切一刀换序重组,判断是否能变为原字符串。但按照该思路写复杂度为 O ( n 2 ) O(n^2) O(n2),不是很理想,因此还是从字符入手。
使用双指针 i,j 从左向右分别指向 s1,s2。i 的任务是遍历 s1,查找 s2 在 s1 中的前缀;j 的任务是标识 s2 中前缀的位置,即 s2[0]~s2[j - 1] 为 s2 与 s1 相同的部分。
以 s1:bunana, s2:nabuna 为例,可以看出,s1:buna | na,s2:na | buna,s1 的后缀和 s2 的前缀想同,均为 na,算法的具体流程如下:
b u n a n a ( s 1 ) i : ↑ n a b u n a ( s 2 ) j : ↑ ⇓ b u n a n a ( s 1 ) i : ↑ n a b u n a ( s 2 ) j : ↑ ⇓ b u n a n a ( s 1 ) i : ↑ n a b u n a ( s 2 ) j : ↑ ⇓ b u n a n a ( s 1 ) i : ↑ n a b u n a ( s 2 ) j : ↑ ⇓ b u n a n a ( s 1 ) i : ↑ n a b u n a ( s 2 ) j : ↑ ⇓ b u n a n a ( s 1 ) i : ↑ n a b u n a ( s 2 ) j : ↑ ⇓ b u n a n a ( s 1 ) i : ↑ n a b u n a ( s 2 ) j : ↑ \begin{array}{l} & b & u & n & a & n & a & (s1)\\ i:& \uparrow & & & & \\ & n & a & b & u & n & a & (s2)\\ j:& \uparrow & & & & \end{array}\\ ~\\\ \Downarrow\\ ~\\\ \begin{array}{l} & b & u & n & a & n & a & (s1)\\ i:& & \uparrow & & & \\ & n & a & b & u & n & a & (s2)\\ j:& \uparrow & & & & \end{array}\\ ~\\\ \Downarrow\\ ~\\\ \begin{array}{l} & b & u & n & a & n & a & (s1)\\ i:& & & \uparrow & & \\ & n & a & b & u & n & a & (s2)\\ j:& \uparrow & & & & \end{array}\\ ~\\\ \Downarrow\\ ~\\\ \begin{array}{l} & b & u & n & a & n & a & (s1)\\ i:& & & & \uparrow & \\ & n & a & b & u & n & a & (s2)\\ j:& & \uparrow & & & \end{array}\\ ~\\\ \Downarrow\\ ~\\\ \begin{array}{l} & b & u & n & a & n & a & (s1)\\ i:& & & & & \uparrow \\ & n & a & b & u & n & a & (s2)\\ j:& \uparrow & & & & \end{array}\\ ~\\\ \Downarrow\\ ~\\\ \begin{array}{l} & b & u & n & a & n & a & (s1)\\ i:& & & & & & \uparrow \\ & n & a & b & u & n & a & (s2)\\ j:& & \uparrow & & & \end{array}\\ ~\\\ \Downarrow\\ ~\\\ \begin{array}{l} & b & u & n & a & n & a & (s1)\\ i:& & & & & & & \uparrow \\ & n & a & b & u & n & a & (s2)\\ j:& & & \uparrow & & \end{array}\\ i:j:b↑n↑uanbaunnaa(s1)(s2) ⇓ i:j:bn↑u↑anbaunnaa(s1)(s2) ⇓ i:j:bn↑uan↑baunnaa(s1)(s2) ⇓ i:j:bnua↑nba↑unnaa(s1)(s2) ⇓ i:j:bn↑uanbaun↑naa(s1)(s2) ⇓ i:j:bnua↑nbaunna↑a(s1)(s2) ⇓ i:j:bnuanb↑aunnaa(s1)↑(s2)
最终,i 指向 s1 的末尾,j 指向 s2 前缀的后一字符,即 s2 后缀的起始位置。
public class Solution {public bool IsFlipedString(string s1, string s2) {int l1 = s1.Length, l2 = s2.Length;if (l1 != l2) return false; // 长度不相等直接否掉int i = 0, j = 0; // 双指针,i 指 s1,j 指 s2while (i < l1) { // 遍历 s1,寻找 s2 的前缀if (s1[i] == s2[j]) j++; // 如果字符相同,则 j 后移else { // 字符不同,则 i、j 回退i -= j;j = 0;}i++; // i 始终前进}i = 0;while (j < l2) { // 检查 s2 后缀是否为 s1 前缀if (s1[i++] != s2[j++]) return false;}return true;}
}
- 时间复杂度:一般情况下为 O ( n ) O(n) O(n),但波动较大。最坏情况为 O ( n 2 ) O(n^2) O(n2),即字符串包含大部分重复字符。可以使用 KMP 算法优化,懒了没必要。
- 空间复杂度: O ( 1 ) O(1) O(1)。
相关文章:

LeetCode 面试题 01.09. 字符串轮转
文章目录 一、题目二、C# 题解 一、题目 字符串轮转。给定两个字符串 s1 和 s2,请编写代码检查 s2 是否为 s1 旋转而成(比如,waterbottle 是 erbottlewat 旋转后的字符串)。 点击此处跳转题目。 示例1: 输入:s1 “wa…...

系统上线安全测评需要做哪些内容?
电力信息系统、航空航天、交通运输、银行金融、地图绘画、政府官网等系统再正式上线前需要做安全测试。避免造成数据泄露从而引起的各种严重问题。 那么系统上线前需要做哪些测试内容呢?下面由我给大家介绍 1、安全机制检测-应用安全 身份鉴别 登录控制模块 应提供…...
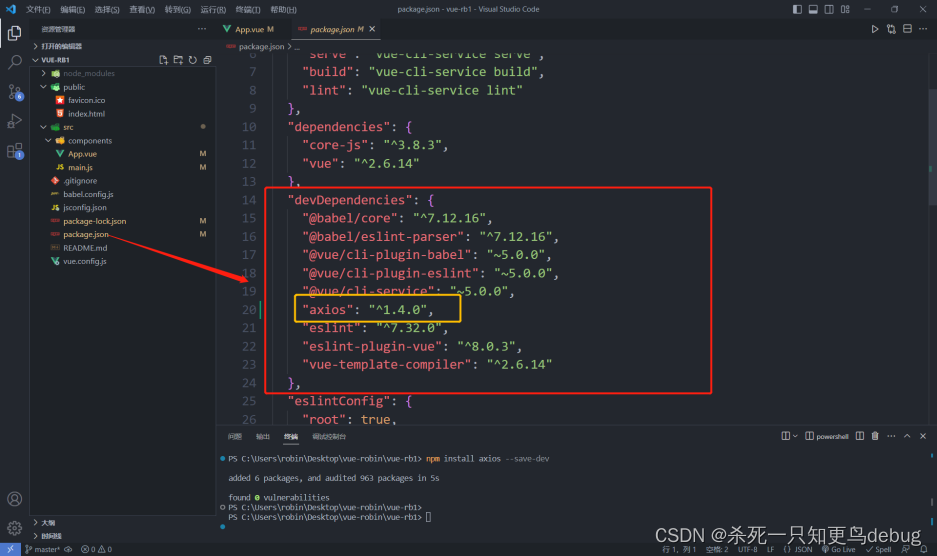
vue 中 axios 的安装及使用
vue 中 axios 的安装及使用 1. axios 安装2. axios使用 1. axios 安装 首先,打开当前的项目终端,输入 npm install axios --save-dev验证是否安装成功,检查项目根目录下的 package.json,其中的 devDependencies 里面会多出一个axios及其版本…...

数据结构——线性数据结构(数组,链表,栈,队列)
文章目录 1. 数组2. 链表2.1. 链表简介2.2. 链表分类2.2.1. 单链表2.2.2. 循环链表2.2.3. 双向链表2.2.4. 双向循环链表 2.3. 应用场景2.4. 数组 vs 链表 3. 栈3.1. 栈简介3.2. 栈的常见应用常见应用场景3.2.1. 实现浏览器的回退和前进功能3.2.2. 检查符号是否成对出现3.2.3. 反…...
多态(C++)
多态 一、初识多态概念“登场”1>. 多态的构成条件2>. 虚函数3>. 虚函数重写(覆盖)4>. 虚函数重写的两个例外1. 协变 一 基类和派生类虚函数返回值类型不同2. 析构函数重写(基类和派生类析构函数名不同) 小结 二、延伸…...

算法leetcode|73. 矩阵置零(rust重拳出击)
文章目录 73. 矩阵置零:样例 1:样例 2:提示:进阶: 分析:题解:rust:go:c:python:java: 73. 矩阵置零: 给定一个 m x n 的矩…...

axios 二次封装
axios 二次封装 基本上每一个项目开发,都必须要二次封装 axios。主要是为了减少重复性工作,不可能每一次发起新请求时,都要重新配置请求域名、请求头 Content-Type、Token 等信息。所以需要把公用的部分都封装成一个函数,每次调用…...

Rust安全之数值
文章目录 数值溢出 数值溢出 编译通过,运行失败 cargo run 1 fn main() {let mut arg std::env::args().skip(1).map(|x| x.parse::<i32>().unwrap()).next().unwrap();let m_i i32::MAX - 1;let a m_i arg;println!("{:?}", a); }thread main panicked…...

4种方法实现html 页面内锚点定位及跳转
使用scrollIntoView进行锚点定位效果 不知道你有没有遇到这样的需求:锚点定位?进入页面某个元素需要出现在可视区?…这一类的需求归根结底就是处理元素与可视区域的关系。我接触了很多前端小伙伴,实现的方式有各种各样的ÿ…...

gitlab配置备忘
版本 gitlab 14.6.2 gitlab备份上传到阿里云oss ### Backup Settings ###! Docs: https://docs.gitlab.com/omnibus/settings/backups.html# gitlab_rails[manage_backup_path] true # gitlab_rails[backup_path] "/var/opt/gitlab/backups"###! Docs: https://…...

基于Centos搭建k8s仓库
系统环境: Red Hat Enterprise Linux 9.1 (Plow) Kernel: Linux 5.14.0-162.6.1.el9_1.x86_64 主机名地址master192.168.19.128node01192.168.19.129node02192.168.19.130 目录 1、关闭防火墙,关闭SElinxu ,开启时间同步服务 2、关…...
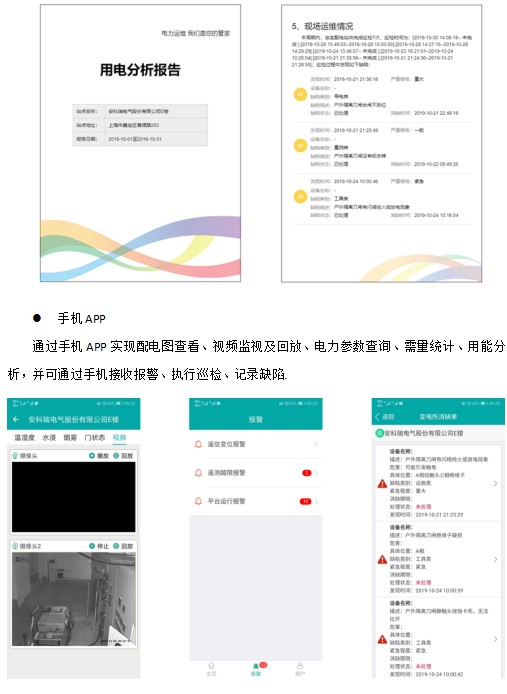
浅谈泛在电力物联网发展形态与技术挑战
安科瑞 华楠 摘 要:泛在电力物联网是当前智能电网发展的一个方向。首先,总结了泛在电力物联网的主要作用和价值体现;其次,从智能电网各个环节概述了物联网技术在电力领域的已有研究和应用基础;进而,构思并…...

git reset --soft 用法
git reset --soft 是 Git 命令中的一个选项,它用于取消之前的提交,并将取消的更改保留在暂存区。这允许您重新组织提交历史或将更改合并到一个新的提交中,而不影响暂存区和工作目录中的更改。 这个命令的语法是: git reset --so…...

哪些测试仪器可以用于检测静电中和设备的性能
静电设备性能测试通常需要使用一些专门的仪器来进行。以下是一些常见的静电设备性能测试仪器: 1. 静电电压测试仪:用于测量物体表面的静电电压。它通常可以测量正负电压,并具有高精度和快速响应的特点。 2. 静电电荷仪:用于测量物…...

浅析 GlusterFS 与 JuiceFS 的架构异同
在进行分布式文件存储解决方案的选型时,GlusterFS 无疑是一个不可忽视的考虑对象。作为一款开源的软件定义分布式存储解决方案,GlusterFS 能够在单个集群中支持高达 PiB 级别的数据存储。自从首次发布以来,已经有超过十年的发展历程。目前&am…...
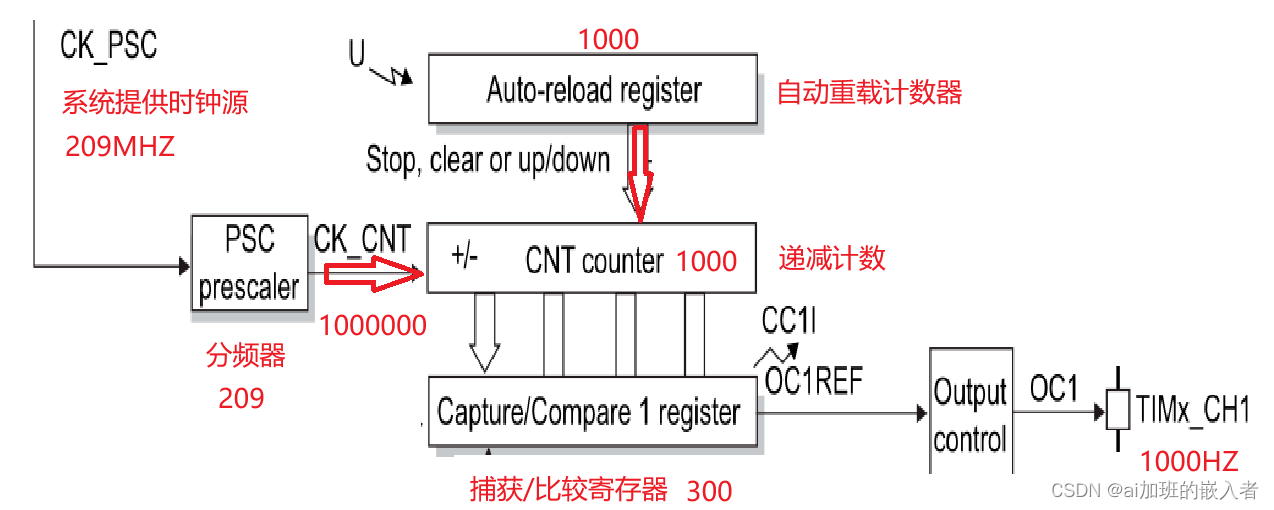
ARM开发,stm32mp157a-A7核PWM实验(驱动蜂鸣器,风扇,马达工作)
1.分析框图; 2.比较捕获寄存器(产生PWM方波); 工作原理: 1、系统提供一个时钟源209MHZ,需要通过分频器进行分频,设置分频器值为209分频; 2、当定时器启动之后,自动重载…...
|消费者需求研究方案)
群狼调研(长沙眼镜店神秘顾客)|消费者需求研究方案
本文由群狼调研(长沙品牌调研)出品,欢迎转载,请注明出处。消费者需求研究方案是在开展研究之前制定的计划,用于指导研究的设计、实施和分析。以下是一个可能的消费者需求研究方案的大致框架: 1. 研究目标和问题: • …...

电脑入门:宽带路由器常见故障排除技巧
宽带路由器在企业网络中的应用是相当广泛的,在运行的过程中出现故障是在所难免的,虽然故障现象多种多样,引起故障发生的原因也不尽相同,但从大体上可以把这些故障分为硬件故障和软件故障,具体来说就是一些网络连接性问题、配置文件选项问题以及网络协议问题等。 由于路由器…...

基于云原生网关的流量防护实践
作者:涂鸦 背景 在分布式系统架构中,每个请求都会经过很多层处理,比如从入口网关再到 Web Server 再到服务之间的调用,再到服务访问缓存或 DB 等存储。在下图流量防护体系中,我们通常遵循流量漏斗原则进行流量防护。…...

开源与云计算:新的合作模式
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...
