当前位置： 首页 > news >正文

Leetcode80. 删除有序数组中的重复项 II

news 2026/2/9 19:25:54

给你一个有序数组 nums ，请你 原地 删除重复出现的元素，使得出现次数超过两次的元素只出现两次 ，返回删除后数组的新长度。

不要使用额外的数组空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。

 

 

 

class Solution {public int removeDuplicates(int[] nums) {int len = nums.length;if(len < 2){return len;}int i = 2;for(int j = i;j < len;j++){if(nums[j] != nums[i-2]){nums[i] = nums[j];i++;}}return i;}
}

相关文章：

Leetcode80. 删除有序数组中的重复项 II

给你一个有序数组 nums &#xff0c;请你 原地 删除重复出现的元素&#xff0c;使得出现次数超过两次的元素只出现两次 &#xff0c;返回删除后数组的新长度。 不要使用额外的数组空间&#xff0c;你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。 class Solu…...

编程日记 2023/8/26 11:20:01

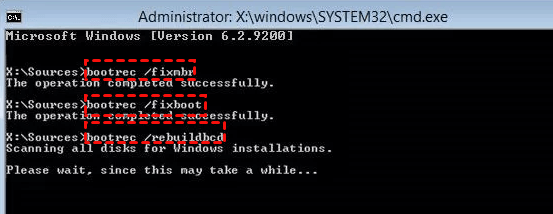
电脑显示“Operating System not found”该怎么办？

“Operating System not found”是一种常见的电脑错误提示&#xff0c;这类错误会导致你无法成功启动Windows。那么电脑显示“Operating System not found”该怎么办呢&#xff1f; 方法1. 检查硬盘 首先&#xff0c;您可以测试硬盘是否存在问题。为此&#xff0c;您可以采取以…...

编程日记 2023/8/26 11:19:00

简析SCTP开发指南

目录 前言一、SCTP基本概念二、SCTP开发步骤1. **环境配置**&#xff1a;2. **建立Socket**&#xff1a;3. **绑定和监听**&#xff1a;4. **接收和发送数据**&#xff1a;5. **关闭连接**&#xff1a; 三、 C语言实现SCTP3.1SCTP客户端代码&#xff1a;3.2 SCTP服务器端代码&a…...

编程日记 2023/8/26 11:17:59

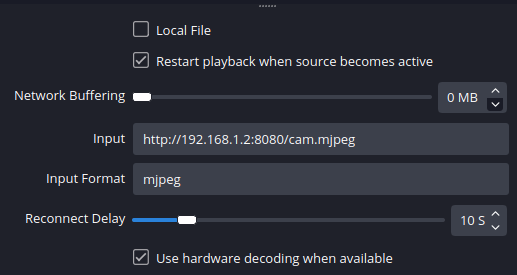
把Android手机变成电脑摄像头

一、使用 DroidCam 使用 DroidCam&#xff0c;你可以将手机作为电脑摄像头和麦克风。一则省钱&#xff0c;二则可以在紧急情况下使用&#xff0c;比如要在电脑端参加一个紧急会议&#xff0c;但电脑却没有摄像头和麦克风。 DroidCam 的安卓端分为免费的 DroidCam 版和收费的 …...

编程日记 2023/8/26 11:16:57

Linux线程篇（中）

有了之前对线程的初步了解我们学习了什么是线程&#xff0c;线程的原理及其控制。这篇文章将继续讲解关于线程的内容以及重要的知识点。 线程的优缺点&#xff1a; 线程的缺点 在这里我们来谈一谈线程健壮性&#xff1a; 首先我们先思考一个问题&#xff0c;如果一个线程出现…...

编程日记 2023/8/26 11:15:55

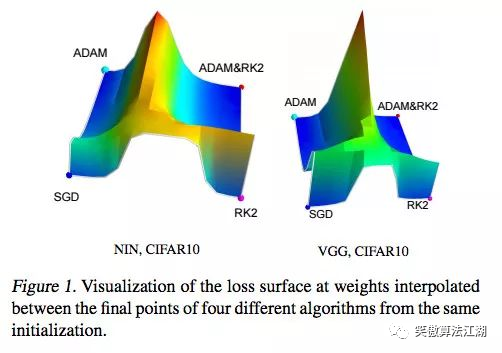
深度学习优化入门：Momentum、RMSProp 和 Adam

目录 深度学习优化入门&#xff1a;Momentum、RMSProp 和 Adam 病态曲率 1牛顿法 2 Momentum:动量 3Adam 深度学习优化入门&#xff1a;Momentum、RMSProp 和 Adam 本文&#xff0c;我们讨论一个困扰神经网络训练的问题&#xff0c;病态曲率。 虽然局部极小值和鞍点会阻碍…...

编程日记 2023/8/26 11:14:54

LeetCode 面试题 01.09. 字符串轮转

文章目录 一、题目二、C# 题解 一、题目 字符串轮转。给定两个字符串 s1 和 s2&#xff0c;请编写代码检查 s2 是否为 s1 旋转而成&#xff08;比如&#xff0c;waterbottle 是 erbottlewat 旋转后的字符串&#xff09;。 点击此处跳转题目。 示例1: 输入&#xff1a;s1 “wa…...

编程日记 2023/8/26 11:13:53

系统上线安全测评需要做哪些内容？

电力信息系统、航空航天、交通运输、银行金融、地图绘画、政府官网等系统再正式上线前需要做安全测试。避免造成数据泄露从而引起的各种严重问题。 那么系统上线前需要做哪些测试内容呢&#xff1f;下面由我给大家介绍 1、安全机制检测-应用安全 身份鉴别 登录控制模块 应提供…...

编程日记 2023/8/26 11:12:50

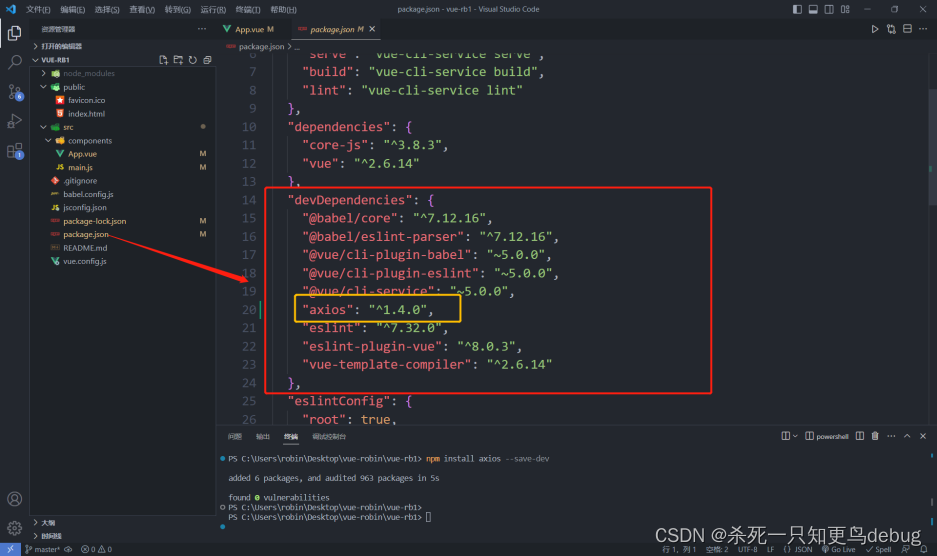
vue 中 axios 的安装及使用

vue 中 axios 的安装及使用 1. axios 安装2. axios使用 1. axios 安装 首先&#xff0c;打开当前的项目终端&#xff0c;输入 npm install axios --save-dev验证是否安装成功&#xff0c;检查项目根目录下的 package.json,其中的 devDependencies 里面会多出一个axios及其版本…...

编程日记 2023/8/26 11:11:48

数据结构——线性数据结构（数组，链表，栈，队列）

文章目录 1. 数组2. 链表2.1. 链表简介2.2. 链表分类2.2.1. 单链表2.2.2. 循环链表2.2.3. 双向链表2.2.4. 双向循环链表 2.3. 应用场景2.4. 数组 vs 链表 3. 栈3.1. 栈简介3.2. 栈的常见应用常见应用场景3.2.1. 实现浏览器的回退和前进功能3.2.2. 检查符号是否成对出现3.2.3. 反…...

编程日记 2023/8/26 11:10:47

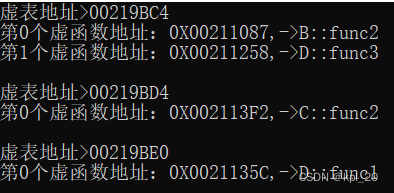
多态（C++）

多态 一、初识多态概念“登场”1>. 多态的构成条件2>. 虚函数3>. 虚函数重写&#xff08;覆盖&#xff09;4>. 虚函数重写的两个例外1. 协变 一 基类和派生类虚函数返回值类型不同2. 析构函数重写&#xff08;基类和派生类析构函数名不同&#xff09; 小结 二、延伸…...

编程日记 2023/8/26 11:09:45

算法leetcode｜73. 矩阵置零（rust重拳出击）

文章目录 73. 矩阵置零&#xff1a;样例 1&#xff1a;样例 2&#xff1a;提示&#xff1a;进阶&#xff1a; 分析&#xff1a;题解&#xff1a;rust&#xff1a;go&#xff1a;c&#xff1a;python&#xff1a;java&#xff1a; 73. 矩阵置零&#xff1a; 给定一个 m x n 的矩…...

编程日记 2023/8/26 11:08:43

axios 二次封装

axios 二次封装 基本上每一个项目开发&#xff0c;都必须要二次封装 axios。主要是为了减少重复性工作&#xff0c;不可能每一次发起新请求时&#xff0c;都要重新配置请求域名、请求头 Content-Type、Token 等信息。所以需要把公用的部分都封装成一个函数&#xff0c;每次调用…...

编程日记 2023/8/26 11:07:41

Rust安全之数值

文章目录 数值溢出 数值溢出 编译通过,运行失败 cargo run 1 fn main() {let mut arg std::env::args().skip(1).map(|x| x.parse::<i32>().unwrap()).next().unwrap();let m_i i32::MAX - 1;let a m_i arg;println!("{:?}", a); }thread main panicked…...

编程日记 2023/8/26 11:06:40

4种方法实现html 页面内锚点定位及跳转

使用scrollIntoView进行锚点定位效果 不知道你有没有遇到这样的需求&#xff1a;锚点定位&#xff1f;进入页面某个元素需要出现在可视区&#xff1f;…这一类的需求归根结底就是处理元素与可视区域的关系。我接触了很多前端小伙伴&#xff0c;实现的方式有各种各样的&#xff…...

编程日记 2023/8/26 11:05:38

gitlab配置备忘

版本 gitlab 14.6.2 gitlab备份上传到阿里云oss ### Backup Settings ###! Docs: https://docs.gitlab.com/omnibus/settings/backups.html# gitlab_rails[manage_backup_path] true # gitlab_rails[backup_path] "/var/opt/gitlab/backups"###! Docs: https://…...

编程日记 2023/8/26 11:04:37

基于Centos搭建k8s仓库

系统环境&#xff1a; Red Hat Enterprise Linux 9.1 (Plow) Kernel: Linux 5.14.0-162.6.1.el9_1.x86_64 主机名地址master192.168.19.128node01192.168.19.129node02192.168.19.130 目录 1、关闭防火墙&#xff0c;关闭SElinxu &#xff0c;开启时间同步服务 2、关…...

编程日记 2023/8/26 11:03:36

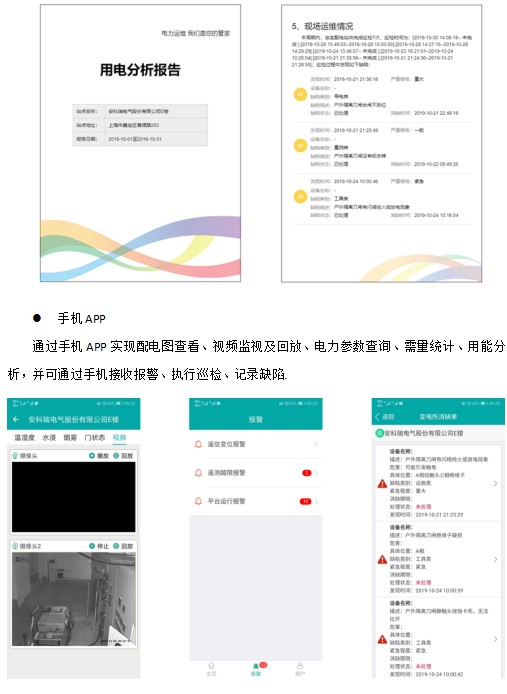
浅谈泛在电力物联网发展形态与技术挑战

安科瑞 华楠 摘 要&#xff1a;泛在电力物联网是当前智能电网发展的一个方向。首先&#xff0c;总结了泛在电力物联网的主要作用和价值体现&#xff1b;其次&#xff0c;从智能电网各个环节概述了物联网技术在电力领域的已有研究和应用基础&#xff1b;进而&#xff0c;构思并…...

编程日记 2023/8/26 11:02:35

git reset --soft 用法

git reset --soft 是 Git 命令中的一个选项&#xff0c;它用于取消之前的提交&#xff0c;并将取消的更改保留在暂存区。这允许您重新组织提交历史或将更改合并到一个新的提交中&#xff0c;而不影响暂存区和工作目录中的更改。 这个命令的语法是&#xff1a; git reset --so…...

编程日记 2023/8/26 11:01:34

哪些测试仪器可以用于检测静电中和设备的性能

静电设备性能测试通常需要使用一些专门的仪器来进行。以下是一些常见的静电设备性能测试仪器&#xff1a; 1. 静电电压测试仪&#xff1a;用于测量物体表面的静电电压。它通常可以测量正负电压&#xff0c;并具有高精度和快速响应的特点。 2. 静电电荷仪&#xff1a;用于测量物…...

编程日记 2023/8/26 11:00:33

7.4.分块查找

一.分块查找的算法思想&#xff1a; 1.实例&#xff1a; 以上述图片的顺序表为例&#xff0c; 该顺序表的数据元素从整体来看是乱序的&#xff0c;但如果把这些数据元素分成一块一块的小区间&#xff0c; 第一个区间[0,1]索引上的数据元素都是小于等于10的&#xff0c; 第二…...

编程新知 2026/2/8 20:43:02

iOS 26 携众系统重磅更新，但“苹果智能”仍与国行无缘

美国西海岸的夏天&#xff0c;再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至&#xff0c;这不仅是开发者的盛宴&#xff0c;更是全球数亿苹果用户翘首以盼的科技春晚。今年&#xff0c;苹果依旧为我们带来了全家桶式的系统更新&#xff0c;包括 iOS 26、iPadOS 26…...

编程新知 2026/2/8 20:41:56

label-studio的使用教程(导入本地路径)

文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

编程新知 2026/2/7 20:40:53

使用分级同态加密防御梯度泄漏

抽象 联邦学习 &#xff08;FL&#xff09; 支持跨分布式客户端进行协作模型训练&#xff0c;而无需共享原始数据&#xff0c;这使其成为在互联和自动驾驶汽车 &#xff08;CAV&#xff09; 等领域保护隐私的机器学习的一种很有前途的方法。然而&#xff0c;最近的研究表明&…...

编程新知 2026/1/24 6:22:43

数据库分批入库

今天在工作中&#xff0c;遇到一个问题&#xff0c;就是分批查询的时候&#xff0c;由于批次过大导致出现了一些问题&#xff0c;一下是问题描述和解决方案&#xff1a; 示例&#xff1a; // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

编程新知 2026/1/8 11:38:36

基于TurtleBot3在Gazebo地图实现机器人远程控制

1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

编程新知 2026/2/6 11:54:58

基于Java+MySQL实现（GUI）客户管理系统

客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息&#xff0c;对客户进行统一管理&#xff0c;可以把所有客户信息录入系统&#xff0c;进行维护和统计功能。可通过文件的方式保存相关录入数据&#xff0c;对…...

编程新知 2026/1/25 10:12:06

动态 Web 开发技术入门篇

一、HTTP 协议核心 1.1 HTTP 基础 协议全称 &#xff1a;HyperText Transfer Protocol&#xff08;超文本传输协议&#xff09; 默认端口 &#xff1a;HTTP 使用 80 端口&#xff0c;HTTPS 使用 443 端口。 请求方法 &#xff1a; GET &#xff1a;用于获取资源&#xff0c;…...

编程新知 2025/10/3 0:42:17

Python+ZeroMQ实战：智能车辆状态监控与模拟模式自动切换

目录 关键点 技术实现1 技术实现2 摘要&#xff1a; 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式&#xff08;自动驾驶、人工驾驶、远程驾驶、主动安全&#xff09;&#xff0c;并通过实时消息推送更新车…...

编程新知 2025/11/12 0:06:50

Spring Security 认证流程——补充

一、认证流程概述 Spring Security 的认证流程基于 过滤器链&#xff08;Filter Chain&#xff09;&#xff0c;核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤&#xff1a; 用户提交登录请求拦…...

编程新知 2026/2/4 17:50:55