【二叉树入门指南】链式结构的实现
【二叉树入门指南】链式结构的实现
- 一、前置说明
- 二、二叉树的遍历
- 2.1前序遍历
- 2.2中序遍历
- 2.3 后序遍历
- 三、以前序遍历为例,递归图解
- 四、层序遍历
- 五、节点个数以及高度等
- 5.1 二叉树节点个数
- 5.2二叉树叶子节点个数
- 5.3 二叉树第k层节点个数
- 5.4 二叉树查找值为x的节点
- 5.5 二叉树的高度
- 六、二叉树的创建和销毁
- 6.1 构建二叉树
- 6.2 二叉树的销毁
- 6.3 判断二叉树是否为完全二叉树

一、前置说明
其他数据结构不同,二叉树的增删查改接口实现的意义不大(后续搜索树的增删查改才有意义)。普通初阶二叉树更重要的是学习控制结构,为后续的AVL树、红黑树等高级数据结构打下基础。同时大部分OJ题也出在此处。
二、二叉树的遍历
所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。

按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
- 前序遍历(Preorder Traversal 亦称先序遍历)——访问顺序:根节点—>左子树—>右子树
- 中序遍历(Inorder Traversal)——访问顺序:左子树—>根节点—>右子树
- 后序遍历(Postorder Traversal)——访问顺序:左子树—>右子树—>根节点
2.1前序遍历
【代码思路】:
- 若二叉树为空,则直接返回。
- 访问根节点。
- 递归遍历左子树,即调用前序遍历函数,传入左子树的根节点。
- 递归遍历右子树,即调用前序遍历函数,传入右子树的根节点
代码:
void PrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%d ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}
2.2中序遍历
【代码思路】:
- 首先判断二叉树是否为空,若为空则直接返回。
- 对当前节点的左子树进行中序遍历,即递归调用中序遍历函数。
- 访问当前节点的值。
- 对当前节点的右子树进行中序遍历,即递归调用中序遍历函数。
代码:
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}
2.3 后序遍历
【代码思路】:
- 判断当前节点是否为空,若为空则返回。
- 递归遍历当前节点的左子树。
- 递归遍历当前节点的右子树。
- 访问当前节点。
代码:
void PostOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}
三、以前序遍历为例,递归图解
前序遍历递归图解:


上述三种遍历结果:
- 前序遍历结果:1 2 3 4 5 6
- 中序遍历结果:3 2 1 5 4 6
- 后序遍历结果:3 2 5 6 4 1
四、层序遍历
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。

【代码思路】:(核心思想:上一层出时带下一层进队列,即根节点出栈时,根节点的孩子节点入栈)
- 首先将根节点入栈。
- 循环进行以下操作,直到栈为空。
。弹出栈顶元素,并将其值输出;
。如果该节点有右子节点,则将右子节点入栈。
。 如果该节点有左子节点,则将左子节点入栈
栈相关代码自行查看:栈和队列代码实现
代码:
void LevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->data);if(front->left)QueuePush(&q, front->left);if (front->right)QueuePush(&q, front->right);}printf("\n");QueueDestroy(&q);
}
五、节点个数以及高度等
5.1 二叉树节点个数
【代码思路】:
- 如果二叉树为空,则节点个数为0。
- 否则,节点个数等于根节点的个数加上左子树的节点个数和右子树的节点个数。
- 递归计算左子树的节点个数。
- 递归计算右子树的节点个数。
- 返回根节点个数加上左子树和右子树的节点个数。
代码:
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
5.2二叉树叶子节点个数
【代码思路】:
- 判断根节点是否为空,若为空,则返回0。
- 判断根节点的左右子树是否为空,若都为空,则表示根节点是叶子节点,返回1。
- 通过递归分别计算左子树和右子树的叶子节点个数,并返回左子树和右子树的叶子节点个数之和。
代码:
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
5.3 二叉树第k层节点个数
【代码思路】:
- 判断二叉树是否为空,如果是则返回0。
- 判断k是否等于1,如果是则返回1,表示当前层为第k层,只有一个节点。
- 如果以上条件都不满足,则递归计算二叉树的左子树和右子树的第k-1层节点个数,然后将左右子树的第k-1层节点个数相加,即为二叉树第k层节点个数。
代码:
int BinaryTreeLevelKSize(BTNode* root, int k)
{assert(k > 0);if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
5.4 二叉树查找值为x的节点
【代码思路】:
- 如果当前节点为空,则返回空。
- 如果当前节点的值等于x,则返回当前节点。
- 否则,递归查找左子树,如果找到则返回左子树中的节点。
- 否则,递归查找右子树,如果找到则返回右子树中的节点。
代码:
BTNode* BTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->data == x)return root;BTNode* ret1 = BTreeFind(root->left, x);if (ret1)return ret1;BTNode* ret2 = BTreeFind(root->right, x);if (ret2)return ret2;return NULL;
}
5.5 二叉树的高度
【代码思路】:
- 如果树为空树,则高度为0。
- 如果树不为空树,则高度为左子树的高度和右子树的高度中的较大值加1。
- 递归地计算左子树和右子树的高度,并取较大值。
- 返回左子树和右子树高度的较大值加1。
代码:
int BinaryTreeHeight(BTNode* root)
{if (root == NULL){return 0;}int LeftHeight = BinaryTreeHeight(root->left);int RightHeight = BinaryTreeHeight(root->right);return LeftHeight > RightHeight ? LeftHeight + 1 : RightHeight + 1;
}
六、二叉树的创建和销毁
6.1 构建二叉树
Tips: 构建二叉树的方式有很多, 这里我们通过前序遍组"ABD##E#H##CF##G##"构建二叉树。(‘#’表示空树)
【代码思路】:
- 如果节点为“#”表示空,返回空。
- 遍历创建左子树,并和根节点链接。
- 遍历创建右子树,并和根节点链接。
- 返回根节点
代码:
typedef int BTDataType;
typedef struct BinaryTreeNode//结构体类型
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;//创建节点
BTNode* BuyNode(BTDataType x)
{BTNode* Node = (BTNode*)malloc(sizeof(BTNode));if (Node == NULL){perror("malloc fail");exit(-1);}Node->data = x;Node->left = NULL;Node->right = NULL;return Node;
}//先序创建二叉树
BTNode* createrroot(char* a, int* pi)
{if (a[*pi] == '#'){(*pi)++;return NULL;}BTNode* root = BuyNode(a[*pi]);(*pi)++;root->left = createrroot(a, pi);root->right = createrroot(a, pi);return root;
}
6.2 二叉树的销毁
【代码思路】:
- 从根节点开始,递归地销毁左子树。
- 从根节点开始,递归地销毁右子树。
- 将根节点从内存中删除。
代码:
void BinaryTreeDestroy(BTNode* root)
{if (root == NULL)return;BinaryTreeDestory(root->left);BinaryTreeDestory(root->right);free(root);
}
6.3 判断二叉树是否为完全二叉树
(博主数据结构初阶是用C语言来实现的,所以此处直接栈代码从博主代码仓库中拷贝过来的,读者可以用其他语言来实现,大同小异)
【代码思路】:
- 遍历二叉树,使用层次遍历的方式,从根节点开始,逐层遍历每个节点。
- 当遇到第一颗空树时停止遍历。
- 从第一颗空树开始,后续节点如果有非空就不是完全二叉树,否则为完全二叉树。
栈相关代码自行查看:栈和队列代码实现
代码:
int BinaryTreeComplete(BTNode* root)
{Que q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);//遇空就跳过if (front==NULL){break;}QueuePush(&q, root->left);QueuePush(&q, root->right);}//检查后续节点是否有非空//有非空就不是完全二叉树while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}


【数据结构入门指南】二叉树顺序结构: 堆及实现(全程配图,非常经典)
相关文章:

【二叉树入门指南】链式结构的实现
【二叉树入门指南】链式结构的实现 一、前置说明二、二叉树的遍历2.1前序遍历2.2中序遍历2.3 后序遍历 三、以前序遍历为例,递归图解四、层序遍历五、节点个数以及高度等5.1 二叉树节点个数5.2二叉树叶子节点个数5.3 二叉树第k层节点个数5.4 二叉树查找值为x的节点5…...
【位运算】算法实战
文章目录 一、算法原理常见的位运算总结 二、算法实战1. leetcode面试题01.01. 判断字符是否唯一2. leetcode268 丢失的数字3. leetcode371 两整数之和4. leetcode004 只出现一次的数字II5. leetcode面试题17.19. 消失的两个数字 三、总结 一、算法原理 计算机中的数据都以二进…...

C++构建系统
收集C构建系统(2023): 跟我一起写Makefile (PDF重制版)CMake tutorialConan, software package manager for C and C developersvcpkg-repovcpkgGoogle Bazel Build System { Fast, Correct } — Choose twoGN gn_quick_start当前Chromium构建系统 GYP Generate You…...

“深入探索JVM内部机制:理解Java虚拟机的运行原理“
标题:深入探索JVM内部机制:理解Java虚拟机的运行原理 摘要:本篇博客将深入探索Java虚拟机(JVM)的内部机制,帮助读者理解JVM的运行原理。我们将介绍JVM的组成结构,包括类加载器、运行时数据区域…...

java八股文面试[JVM]——双亲委派模型
1.当AppClassLoader去加载一个class时,它首先不会自己去尝试加载这个类,而是把类加载请求委托给父加载器ExtClassLoader去完成。 2.当ExtClassLoader去加载一个class时,它首先也不会去尝试加载这个类,而是把类加载请求委托给父加载…...

NLP与大模型主题全国师资培训班落地,飞桨持续赋能AI人才培养
为了推动大模型及人工智能相关专业人员的培养,8月11日-8月13日,由中国计算机学会主办、机械工业出版社、北京航空航天大学、百度飞桨联合承办 “CCF群星计划之文心高校行- NLP与大模型”主题师资培训班(以下简称培训班)在北京天信…...

Jupyter Notebook 配置根目录
注:本文是在 Windows 10 上配置 Jupyter Notebook 打开的默认根目录,Linux 同。 步骤一:创建 Jupyter Notebook 配置文件 使用以下命令创建 Jupyter Notebook 配置文件(如果尚未创建): jupyter notebook …...

算法 位运算
文章目录 一、&(按位与)运算符二、|(按位或)运算符三、^(异或)运算符四、~(取反)运算符五、<<(左移)运算符六、>>(右移ÿ…...

Linux 虚拟机常用命令
一、文件/文件夹管理 1. ls命令 就是 list 的缩写,通过 ls 命令不仅可以查看 linux 文件夹包含的文件,而且可以查看文件权限(包括目录、文件夹、文件权限)查看目录信息等等。 ls -a 列出目录所有文件,包含以.开始的隐藏文件ls -A 列出除.…...
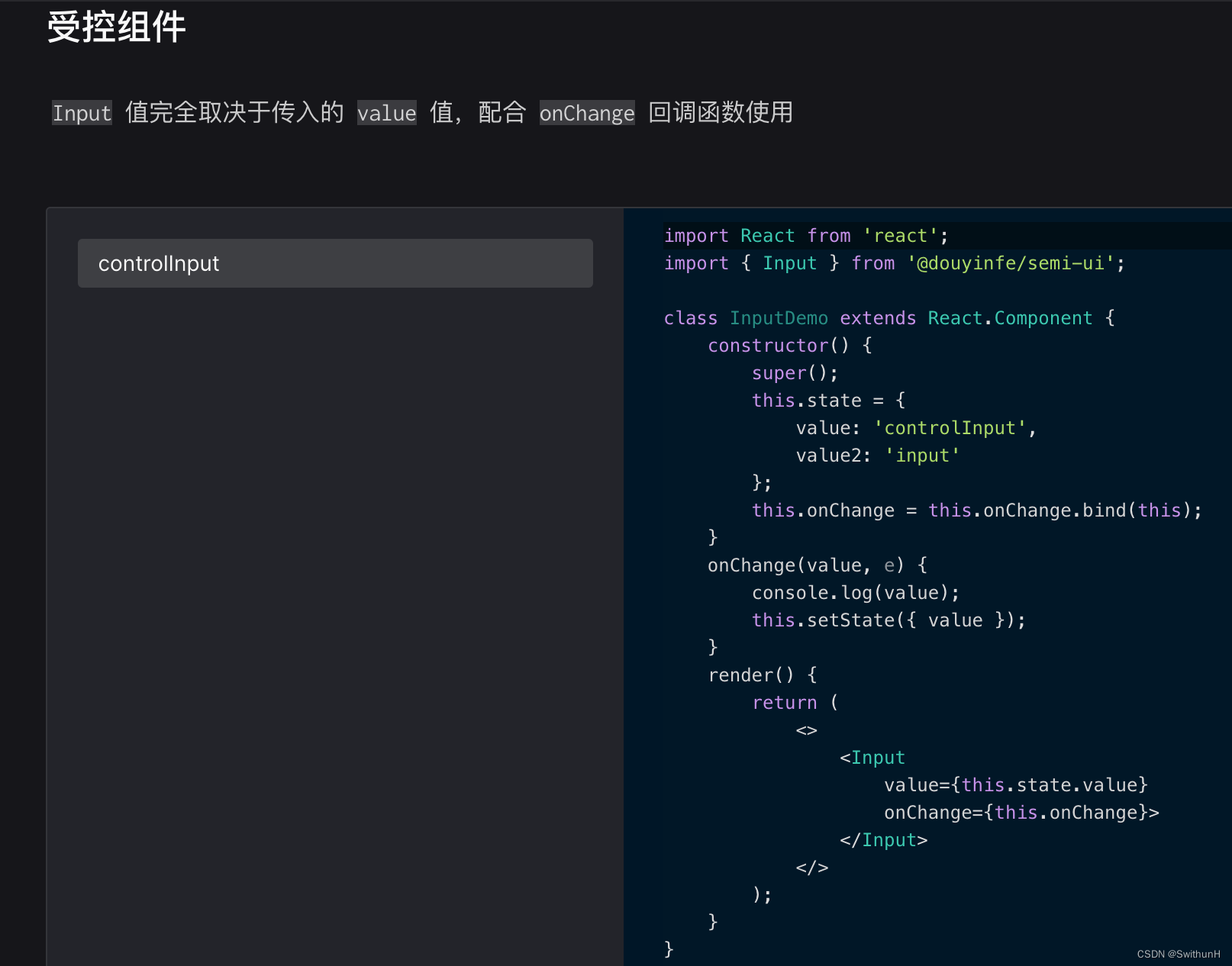
解决抖音semi-ui的Input无法获取到onChange事件
最近在使用semi-ui框架的Input实现一个上传文件功能时遇到了坑,就是无法获取到onChange事件,通过console查看只是拿到了一个文件名。但若是把<Input>换成原生的<input>,就可以正常获取到事件。仔细看了下官方文档,发现…...
免费的png打包plist工具CppTextu,一款把若干资源图片拼接为一张大图的免费工具
经常做游戏打包贴图的都知道,要把图片打包为一张或多张大图,要使用打包工具TexturePacker。 TexturePacker官方版可以直接导入PSD、SWF、PNG、BMP等常见的图片格式,主要用于网页、游戏和动画的制作,它可以将多个小图片汇聚成一个…...
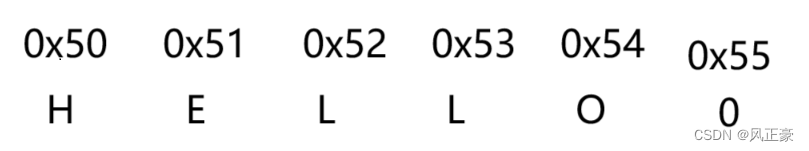
深层次分析字符数组和字符串的区别是什么?
前言 (1)休闲时刻刷B站,看到一个卖课的,发视频问,char arr1[]{‘H’,‘E’,‘L’,‘L’,‘O’};和char arr2[]“HELLO”;区别是什么。 (2)看那个卖课博主一顿分析,最后成功得出&…...
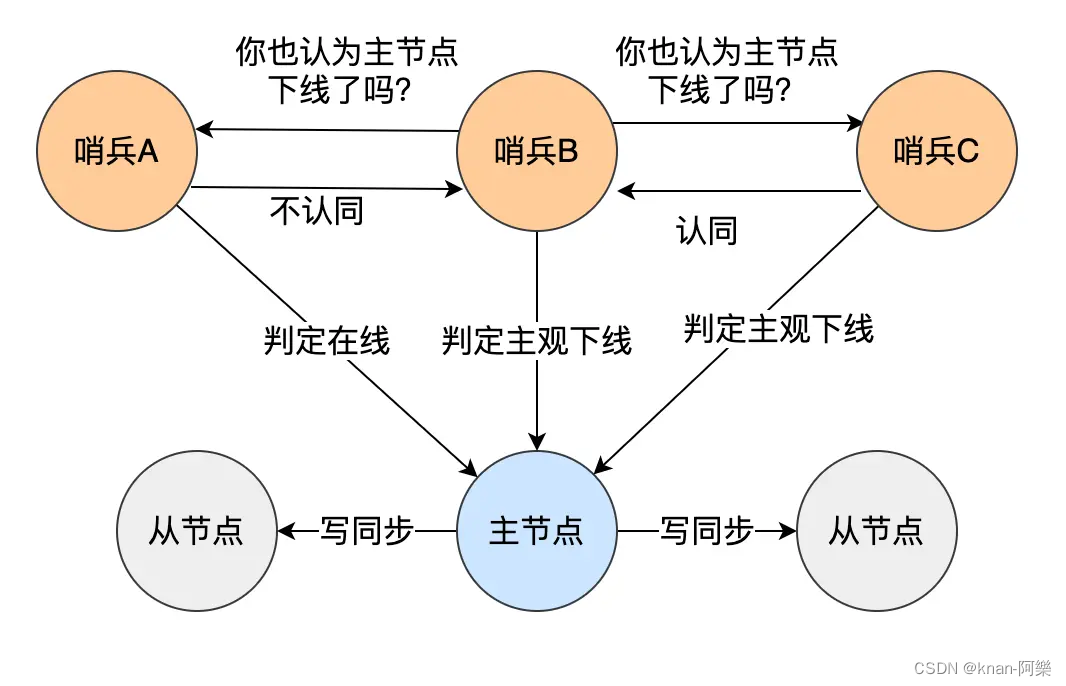
Redis 的主从复制、哨兵模式、集群脑裂
主从复制 主从复制是 Redis 高可用服务最基础的保证,将一台 Redis 主服务器,同步数据到多台 Redis 从服务器上,即一主多从的模式,且主从服务器之间采用的是「读写分离」的方式。 主服务器可以进行读写操作,当发生写操…...

Pycharm通过SSH配置centos上Spark环境
直接在shell进行pyspark进行编程,程序没有办法写得太长,而且我们希望能够实现一个及时给出结果的编程环境,可以使用pycharm连接centos上的spark,进行本地编程,同步到centos系统中运行程序,并把结果返回pych…...

leetcode做题笔记98. 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。 有效 二叉搜索树定义如下: 节点的左子树只包含 小于 当前节点的数。节点的右子树只包含 大于 当前节点的数。所有左子树和右子树自身必须也是二叉搜索树。 思路一:递归 …...

C# 中Lambda中的的匿名函数
/// <summary>/// 根据设备号,获取故障列表/// </summary>/// <param name"scanCode">主键</param>/// <returns></returns>[HttpGet]public async Task<IActionResult> GetItemPageList(string scanCode){//v…...

铰接式车辆的横向动力学仿真提供车辆模型研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Ubuntu20 安装 libreoffice
1 更新apt-get sudo apt-get update2 安装jdk 查看jdk安装情况 Command java not found, but can be installed with:sudo apt install default-jre # version 2:1.11-72, or sudo apt install openjdk-11-jre-headless # version 11.0.138-0ubuntu1~20.04 sud…...

HTTP协议(JavaEE初阶系列15)
目录 前言: 1.HTTP协议 1.1HTTP协议是什么 1.2HTTP协议的报文格式 1.2.1抓包工具的使用 1.2.2HTTP请求 1.2.3HTTP响应 2.HTTP请求 2.1首行的组成 2.2.1URL的组成 2.2认识“方法”(method) 2.2.1GET方法 2.2.2POST方法 2.2.3GET…...
)
机器学习基础10-审查回归算法(基于波士顿房价的数据集)
上一节介绍了如何审查分类算法,并介绍了六种不同的分类算法,还 用同一个数据集按照相同的方式对它们做了审查,本章将用相同的方式对回归算法进行审查。 在本节将学到: 如何审查机器学习的回归算法。如何审查四种线性分类算法。如…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

Java数组Arrays操作全攻略
Arrays类的概述 Java中的Arrays类位于java.util包中,提供了一系列静态方法用于操作数组(如排序、搜索、填充、比较等)。这些方法适用于基本类型数组和对象数组。 常用成员方法及代码示例 排序(sort) 对数组进行升序…...
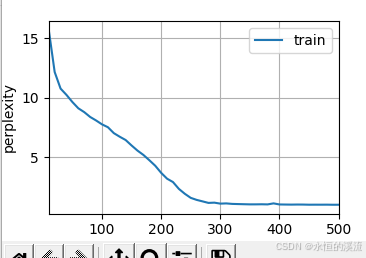
李沐--动手学深度学习--GRU
1.GRU从零开始实现 #9.1.2GRU从零开始实现 import torch from torch import nn from d2l import torch as d2l#首先读取 8.5节中使用的时间机器数据集 batch_size,num_steps 32,35 train_iter,vocab d2l.load_data_time_machine(batch_size,num_steps) #初始化模型参数 def …...

CVE-2023-25194源码分析与漏洞复现(Kafka JNDI注入)
漏洞概述 漏洞名称:Apache Kafka Connect JNDI注入导致的远程代码执行漏洞 CVE编号:CVE-2023-25194 CVSS评分:8.8 影响版本:Apache Kafka 2.3.0 - 3.3.2 修复版本:≥ 3.4.0 漏洞类型:反序列化导致的远程代…...
