【数据结构】 栈(Stack)的应用场景
文章目录
- 🌏前言
- 🍀改变元素的序列
- 🚩场景一
- 📌解析:
- 🚩场景二
- 📌解析:
- 🎍将递归转化为循环
- 🌳[括号匹配](https://leetcode.cn/problems/valid-parentheses/)
- 🚩题目描述:
- 🚩示例:
- 🚩思路解析:
- 🚩代码实现:
- 🎄[逆波兰表达式求值](https://leetcode.cn/problems/evaluate-reverse-polish-notation/)
- 🐱👤拓展逆波兰式
- 🐱👓什么叫做逆波兰表达式
- 🐱🐉逆波兰表达式算法步骤
- 🚩题目描述
- 🚩示例:
- 🚩解法思路
- 🌴[出栈入栈次序匹配](https://www.nowcoder.com/practice/d77d11405cc7470d82554cb392585106?tpId=13&&tqId=11174&rp=1&ru=/activity/oj&qru=/ta/coding-interviews/question-ranking)
- 🚩题目描述:
- 🚩示例
- 🚩解法思路:
- 🚩代码实现:
- 🌲[最小栈](https://leetcode.cn/problems/min-stack/description/)
- 🚩题目描述:
- 🚩示例:
- 🚩思路解析:
- 📌将元素val推入堆栈
- 📌删除堆栈顶部的元素
- 📌获取堆栈顶部的元素
- 📌获取堆栈中的最小元素
- 🚩完整代码:
- ⭕总结
🌏前言
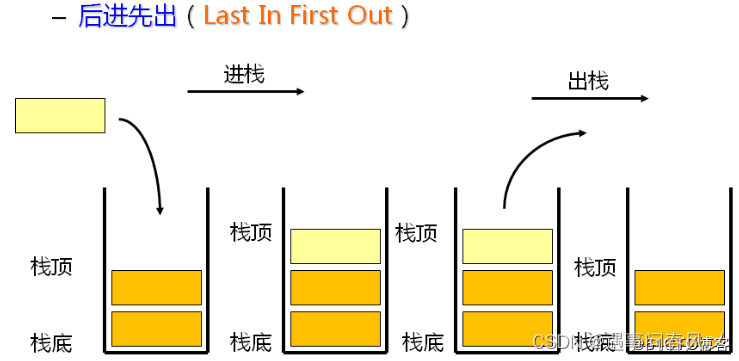
栈(Stack)又名堆栈,作为一个== 先进后出== 的数据结构。
它是一种运算受限的线性表。其限制是仅允许在表的一端进行插入和删除运算。这一端被称为栈顶,相对地,把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈,它是把新元素放到栈顶元素的上面,使之成为新的栈顶元素;从一个栈删除元素又称作出栈或退栈,它是把栈顶元素删除掉,使其相邻的元素成为新的栈顶元素。
🍀改变元素的序列
🚩场景一
- 若进栈序列为 1,2,3,4 ,进栈过程中可以出栈,则下列不可能的一个出栈序列是(C)
A: 1,4,3,2 B: 2,3,4,1 C: 3,1,4,2 D: 3,4,2,1
📌解析:
- A选项进出入栈顺序:
- push(1)->push(2)->push(3)->push(4)->pop(4)->pop(3)->pop(2);
- B选型的出入栈顺序:
- push(1)->push(2)->pop(2)->push(3)->pop(3)->push(4)->pop(4)->pop(1);
- C选项出入栈顺序:
- push(1)->push(2)->push(3)->pop(3)------->?pop(1)
- 这时候我们的我们的栈内元素为:
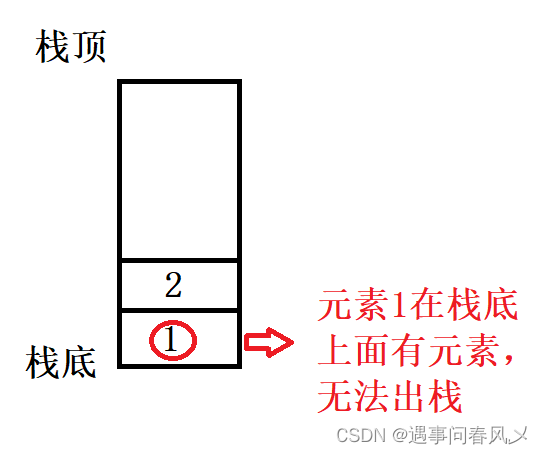
- 所以C选项错误
- D选项出入栈顺序:
- pusn(1)->push(2)->push(3)->pop(3)->push(4)->pop(4)->pop(2)->pop(1);
🚩场景二
- 一个栈的初始状态为空。现将元素1、2、3、4、5、A、B、C、D、E依次入栈,然后再依次出栈,则元素出栈的顺序是( B )。
A: 12345ABCDE B: EDCBA54321
C: ABCDE12345 D: 54321EDCBA
📌解析:
依次入栈后,栈内元素为:
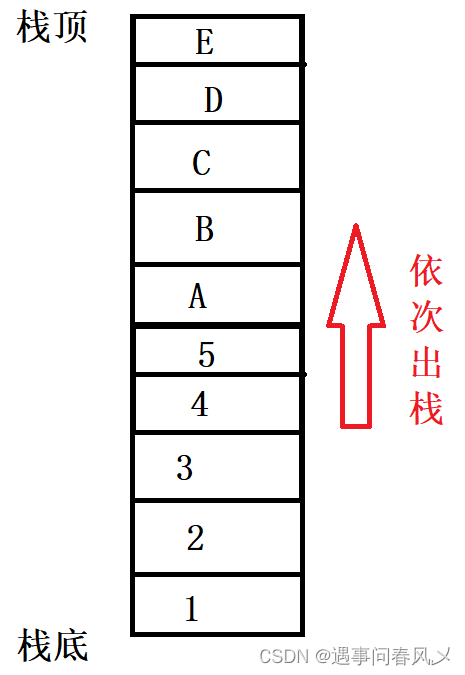
所以答案为B;
🎍将递归转化为循环
比如:逆序打印链表
在我们没有学习栈以前,我们可能会使用递归的方法进行打印,如下所示:
// 递归方式void printList(Node head){if(null != head){printList1(head.next);System.out.print(head.val + " ");}}// 循环方式void printList1(Node head) {if (null == head) {return;}}
其实我们发现逆序打印链表的本质不就是:排在前面的后打印,排在后面的先打印
这不就是栈先进后出的思想吗
所以我们可以先让链表的每一个依次进栈,再出栈即可,实现如下:
Stack<Node> s = new Stack<>();
// 将链表中的结点保存在栈中Node cur = head;while(null != cur){s.push(cur);cur = cur.next;}// 将栈中的元素出栈while(!s.empty()){System.out.print(s.pop().val + " ");}🌳括号匹配
🚩题目描述:
给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 每个右括号都有一个对应的相同类型的左括号。
class Solution {public boolean isValid(String s) {}
}
🚩示例:

🚩思路解析:
我们利用栈的方法进行解决:
- 如果是左括号,就让他进栈
- 如果是右括号,就让它与栈顶元素进行比较
- 如果栈顶元素与该右括号构成一对,则让栈顶元素出栈
- 若不是一对,则返回false;
特殊情况考虑:
- 右括号进来时栈为空,此时直接返回false就好
- 左括号太多,遍历完后,栈内还有元素,这时候需要进行为空的判断
- 若为空,返回true;反之则为false;
🚩代码实现:
class Solution {public boolean isValid(String s) {Stack<Character> characterStack = new Stack<>();for(int i = 0;i < s.length(); i++) {char ch1 = s.charAt(i);if(ch1 == '('||ch1 == '{' || ch1 == '[') {characterStack.push(ch1);} else {if(characterStack.empty()) {return false;}char ch2 = characterStack.peek();if(ch2 == '('&&ch1 == ')' ||ch2 == '{'&&ch1 == '}' ||ch2 == '['&&ch1 == ']') {characterStack.pop();} else {return false;}}}if(characterStack.empty()) {return true;}return false;}
}
🎄逆波兰表达式求值
🐱👤拓展逆波兰式
🐱👓什么叫做逆波兰表达式
逻辑提问式类似于算术表达式,对于检索而言,这种表达式并不是最优和最简洁的形式,需要进行必要的转换。
1929年波兰的逻辑学家卢卡西维兹(Jan Lucasiewicz)提出了将运算符放在运算项后面的逻辑表达式,又称“逆波兰表达式”。
采用这种表达式组织逻辑提问式非常方便检索运算,是日本的福岛先生最早将逆波兰表达式应用于情报检索的,故又称为“福岛方法”。 [2]
逆波兰表达式又叫做后缀表达式,是一种没有括号,并严格遵循“从左到右”运算的后缀式表达方法,如下表所示:
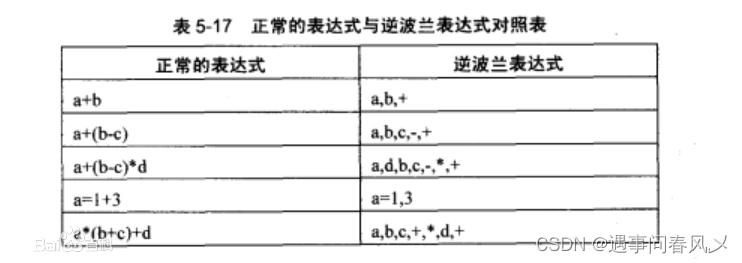
🐱🐉逆波兰表达式算法步骤
-
首先构造一个运算符栈,此运算符在栈内遵循越往栈顶优先级越高的原则。
-
读入一个用中缀表示的简单算术表达式,为方便起见,设该简单算术表达式的右端多加上了优先级最低的特殊符号“#”。
-
从左至右扫描该算术表达式,从第一个字符开始判断,如果该字符是数字,则分析到该数字串的结束并将该数字串直接输出。
-
如果不是数字,该字符则是运算符,此时需比较优先关系。具体做法是:将该字符与运算符栈顶的运算符的优先关系相比较。如果该字符优先关系高于此运算符栈顶的运算符,则将该运算符入栈。若不是的话,则将栈顶的运算符从栈中弹出,直到栈项运算符的优先级低于当前运算符,将该字符入栈。
-
重复步骤1~2,直至扫描完整个简单算术表达式,确定所有字符都得到正确处理,便可以将中缀式表示的简单算术表达式转化为逆波兰表示的简单算术表达式。
🚩题目描述
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
🚨注意:
- 有效的算符为 ‘+’、‘-’、‘*’ 和 ‘/’ 。
- 每个操作数(运算对象)都可以是一个整数或者另一个表达式。
- 两个整数之间的除法总是 向零截断 。
- 表达式中不含除零运算。
- 输入是一个根据逆波兰表示法表示的算术表达式。
- 答案及所有中间计算结果可以用 32 位 整数表示。
class Solution {public int evalRPN(String[] tokens) {}
}
🚩示例:

🚩解法思路
如果当前字符为数字,则压栈,如果是运算符,则将栈顶两个元素弹出作相应运算,结果再入栈,最后当表达式扫描完后,栈里的就是结果。
🚨注意:先出来的数为左操作数,后出来的数为右操作数
代码实现如下:
class Solution {public int evalRPN(String[] tokens) {Stack<Integer> stack = new Stack<>();for(String x : tokens){if(!isOperation(x)) {stack.push(Integer.parseInt(x));}else {int num2 = stack.pop();int num1 = stack.pop();switch (x) {case "+":stack.push(num1+num2);break;case "-":stack.push(num1-num2);break;case "*":stack.push(num1*num2);break;case "/":stack.push(num1/num2);break;}}}return stack.pop();}private boolean isOperation(String x) {if (x.equals("+") || x.equals("-") || x.equals("/") || x.equals("*")) {return true;}return false;}}
🌴出栈入栈次序匹配
🚩题目描述:
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹出序列。
- 0<=pushV.length == popV.length <=1000
- -1000<=pushV[i]<=1000
- pushV 的所有数字均不相同
🚩示例

🚩解法思路:
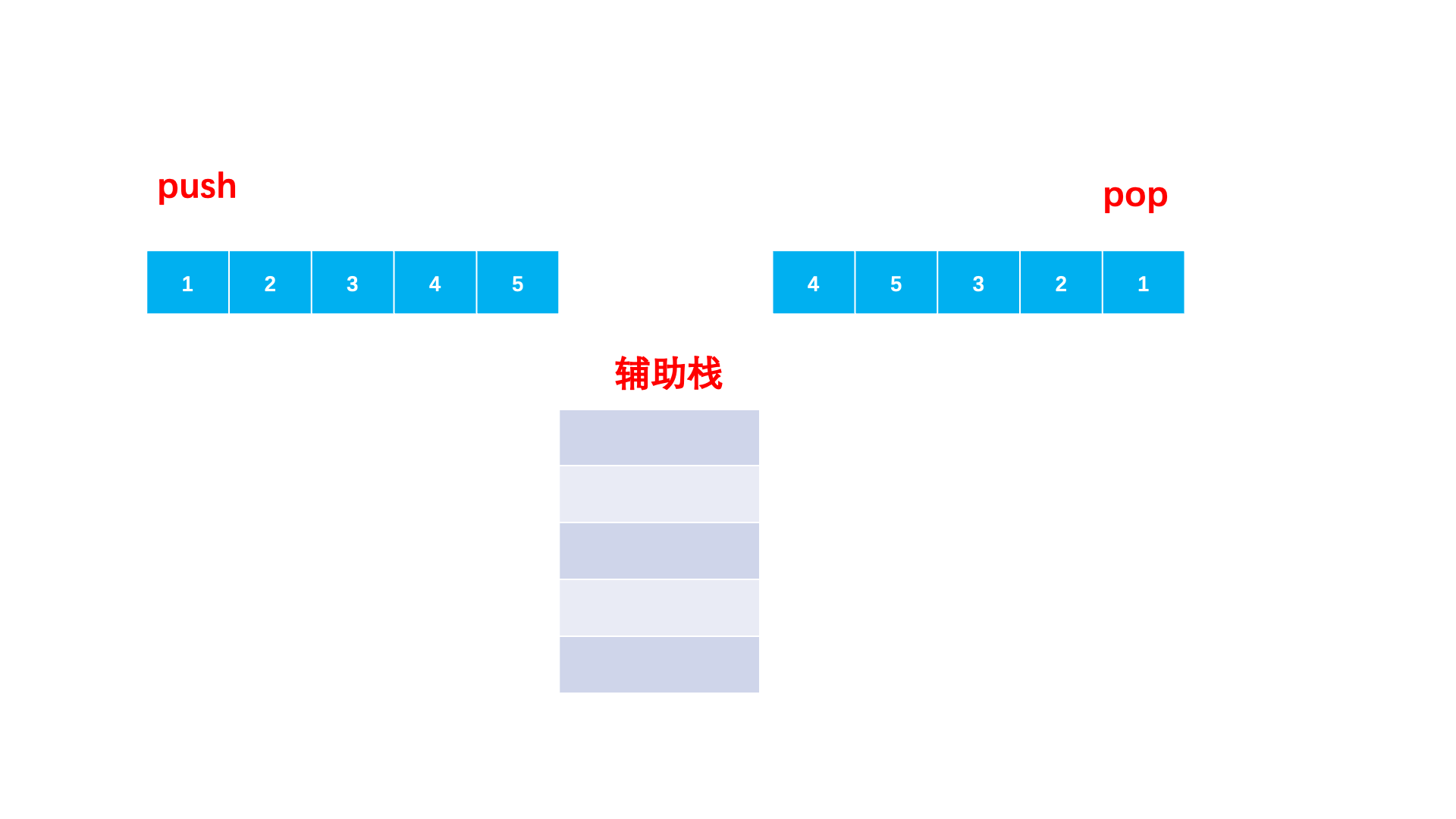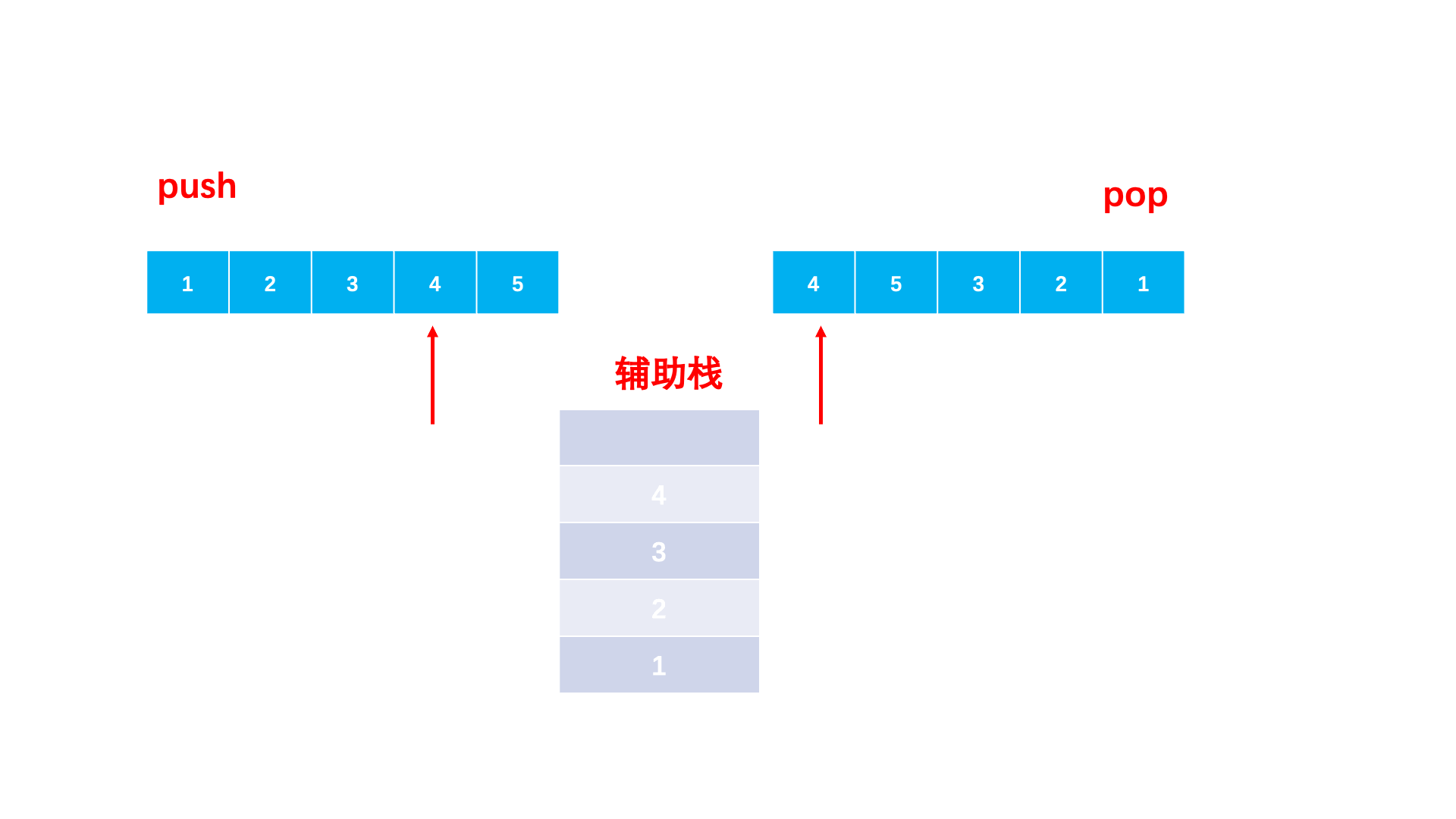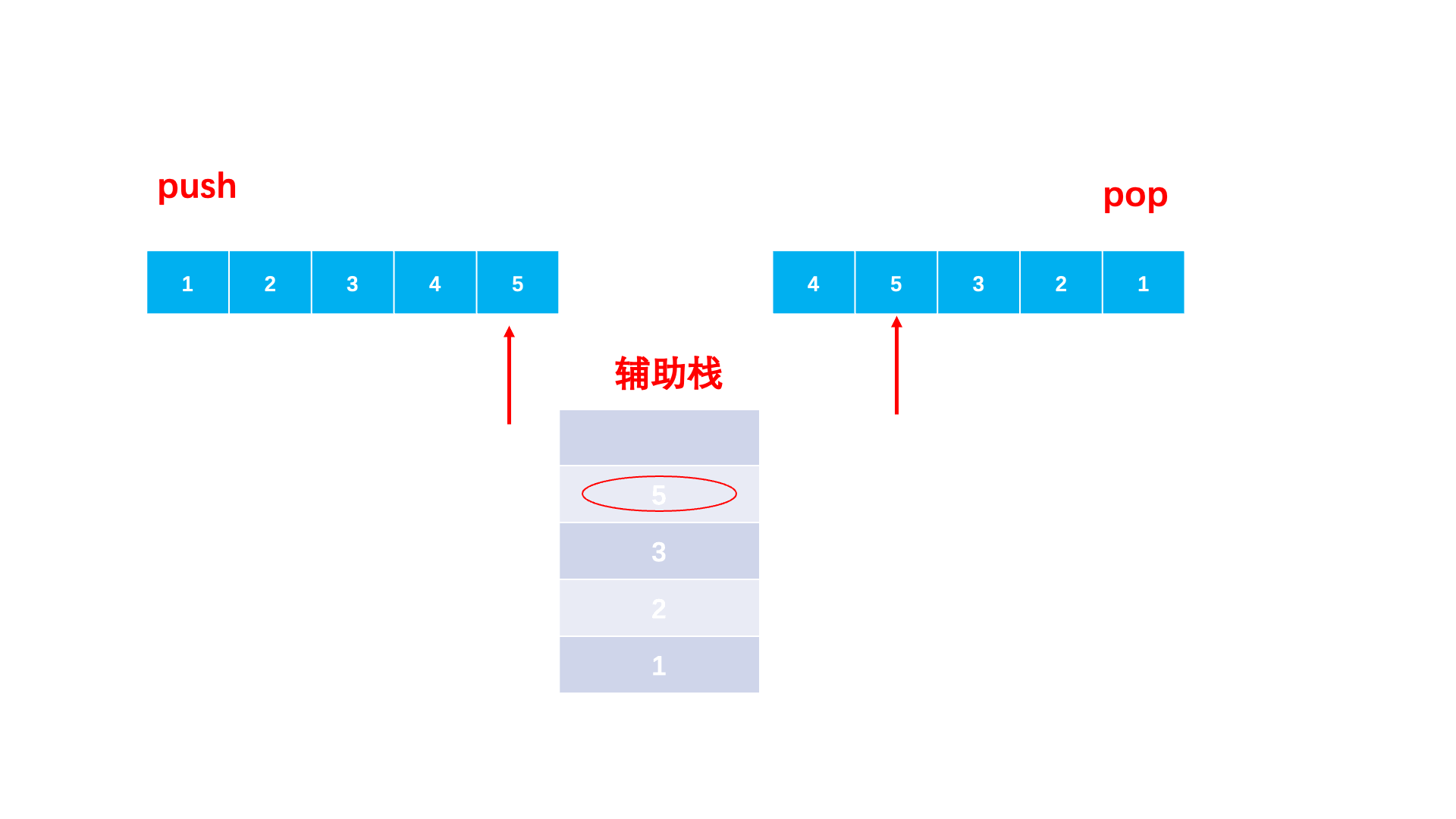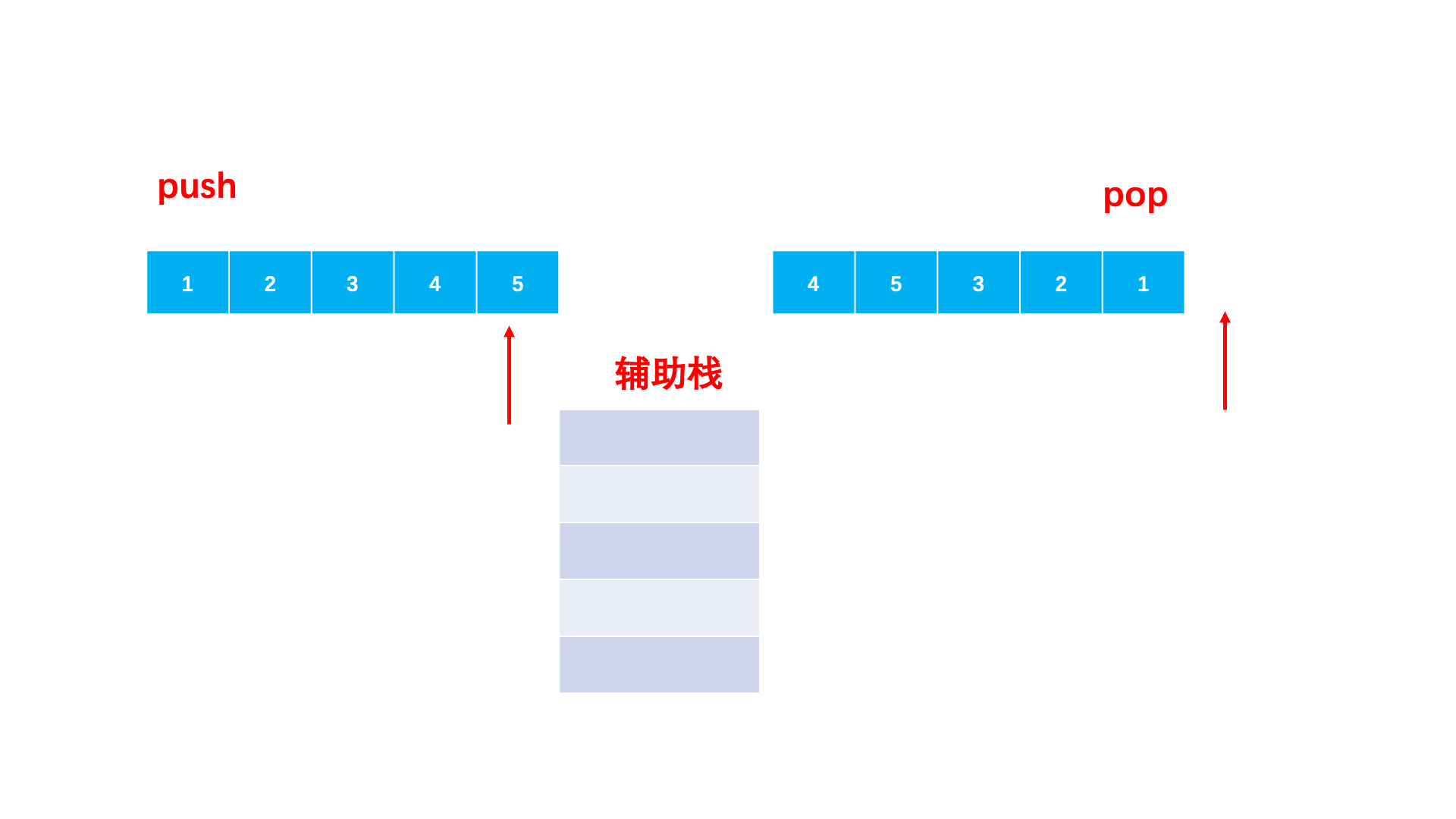
我们就可以用一个栈来模拟。对于入栈序列,只要栈为空,序列肯定要依次入栈。那什么时候出来呢?自然是遇到一个元素等于当前的出栈序列的元素,那我们就放弃入栈,让它先出来。
具体做法:
- 准备一个辅助栈,两个下标分别访问两个序列。
- 辅助栈为空或者栈顶不等于出栈数组当前元素,就持续将入栈数组加入栈中。
- 栈顶等于出栈数组当前元素就出栈。
- 当入栈数组访问完,出栈数组无法依次弹出,就是不匹配的,否则两个序列都访问完就是匹配的。
🚩代码实现:
import java.util.Stack;
public class Solution {public boolean IsPopOrder(int [] pushA,int [] popA) {int n = pushA.length;//辅助栈Stack<Integer> s = new Stack<>();//遍历入栈的下标int j = 0;//遍历出栈的数组for(int i = 0; i < n; i++){//入栈:栈为空或者栈顶不等于出栈数组while(j < n && (s.isEmpty() || s.peek() != popA[i])){s.push(pushA[j]);j++;}//栈顶等于出栈数组if(s.peek() == popA[i])s.pop();//不匹配序列elsereturn false;}return true;}
}🌲最小栈
🚩题目描述:
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
- MinStack() 初始化堆栈对象。
- void push(int val) 将元素val推入堆栈。
- void pop() 删除堆栈顶部的元素。
- int top() 获取堆栈顶部的元素。
- int getMin() 获取堆栈中的最小元素。
class MinStack {public MinStack() {}public void push(int val) {}public void pop() {}public int top() {}public int getMin() {}
}/*** Your MinStack object will be instantiated and called as such:* MinStack obj = new MinStack();* obj.push(val);* obj.pop();* int param_3 = obj.top();* int param_4 = obj.getMin();*/
🚩示例:

🚩思路解析:
我们创建两个栈
- 一个用来存放我们的全部数据->stack
- 一个用来存放最小栈->minStack
private Stack<Integer> stack ;private Stack<Integer> minStack ;public MinStack() {stack = new Stack<>();minStack = new Stack<>();}
📌将元素val推入堆栈
做法如下:
- stack无差别推入
- 对于minStack进行判断,若为空,直接压入
- 若不为空,则需要与栈顶元素进行比较
- 若小于等于,则压入
代码实现如下:
public void push(int val) {stack.push(val);if(minStack.empty()) {minStack.push(val);}else {if(val <= minStack.peek()) {minStack.push(val);}}}
📌删除堆栈顶部的元素
做法如下:
- 对stack进行判断判断,若不为空。怎进行删除
- 同样我们的minStack也需要进行判断,判断条件为:若栈顶元素等于stack所删除元素
- 则minStack栈顶元素也要删除,目的时维护最小栈
代码实现如下:
public void pop() {if(!stack.empty()) {Integer val = stack.pop();//维护最小栈if (val.equals(minStack.peek())) {minStack.pop();}}}
📌获取堆栈顶部的元素
-
做一个是否为空的判断
-
若不为直接返回栈顶元素就好
-
若为空返回-1
代码实现如下:
// peekpublic int top() {if(!stack.empty()) {return stack.peek();}return -1;}
📌获取堆栈中的最小元素
直接返回minStack栈顶元素就好
public int getMin() {return minStack.peek();}
🚩完整代码:
class MinStack {private Stack<Integer> stack ;private Stack<Integer> minStack ;public MinStack() {stack = new Stack<>();minStack = new Stack<>();}public void push(int val) {stack.push(val);if(minStack.empty()) {minStack.push(val);}else {if(val <= minStack.peek()) {minStack.push(val);}}}public void pop() {if(!stack.empty()) {Integer val = stack.pop();//维护最小栈if (val.equals(minStack.peek())) {minStack.pop();}}}// peekpublic int top() {if(!stack.empty()) {return stack.peek();}return -1;}public int getMin() {return minStack.peek();}
}/*** Your MinStack object will be instantiated and called as such:* MinStack obj = new MinStack();* obj.push(val);* obj.pop();* int param_3 = obj.top();* int param_4 = obj.getMin();*/
⭕总结
关于《【数据结构】 栈(Stack)的应用场景》就讲解到这儿,感谢大家的支持,欢迎各位留言交流以及批评指正,如果文章对您有帮助或者觉得作者写的还不错可以点一下关注,点赞,收藏支持一下!
相关文章:

【数据结构】 栈(Stack)的应用场景
文章目录 🌏前言🍀改变元素的序列🚩场景一📌解析: 🚩场景二📌解析: 🎍将递归转化为循环🌳[括号匹配](https://leetcode.cn/problems/valid-parentheses/)&…...
人力资源小程序的设计原则与实现方法
随着移动互联网的快速发展,小程序成为了各行各业推广和服务的新利器。对于人力资源行业来说,开发一款定制化的小程序不仅可以提升服务效率,还可以增强品牌形象和用户粘性。那么,如何定制开发人力资源类的小程序呢?下面…...

检查Javascript对象数组中是否存在对象值,如果没有向数组添加新对象
需求: 如果我有以下对象数组: [ { id: 1, username: fred }, { id: 2, username: bill }, { id: 2, username: ted } ]有没有办法循环遍历数组,以检查特定的用户名值是否已经存在,如果它什么都不做,但是如果它没有用…...
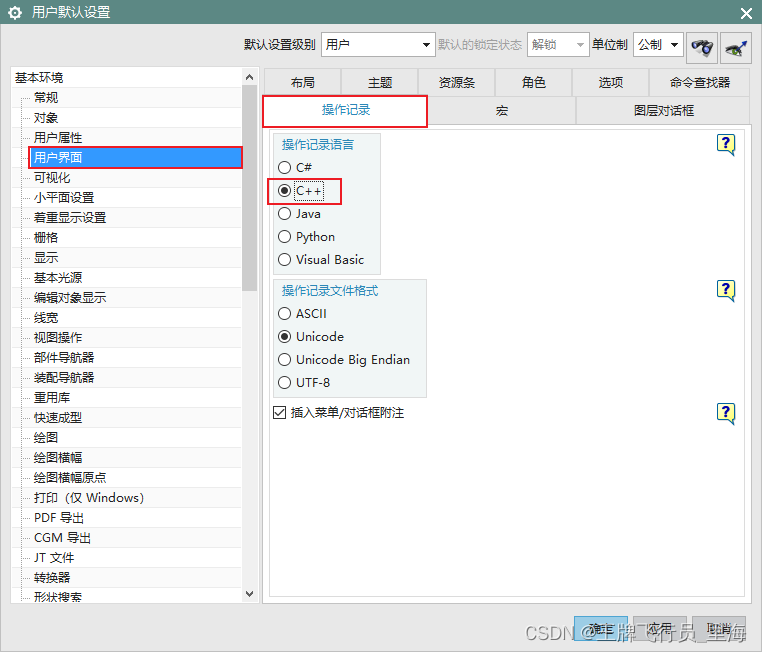
UG\NX二次开发 使用录制功能录制操作记录时,如何设置默认的开发语言?
文章作者:里海 来源网站:王牌飞行员_里海_里海NX二次开发3000例,C\C,Qt-CSDN博客 简介: NX二次开发使用BlockUI设计对话框时,如何设置默认的代码语言? 效果: 方法: 依次打开“文件”->“实用…...
【业务功能篇83】微服务SpringCloud-ElasticSearch-Kibanan-docke安装-应用层实战
五、ElasticSearch应用 1.ES 的Java API两种方式 Elasticsearch 的API 分为 REST Client API(http请求形式)以及 transportClient API两种。相比来说transportClient API效率更高,transportClient 是通过Elasticsearch内部RPC的形式进行请求…...
VBJSON报错:缺少:语句结束
项目中使用JSON库VBJSON时报错: 编译错误:缺少:语句结束 cJSONScript和cStringBuilder报相同的错误,都在第一行: VERSION 1.0 CLASS 研究了半天没啥结果,之前使用这个库的时候没有什么问题,所以判定是当前…...
Docker安装ES+kibana8.9.1
参考:基于Docker安装Elasticsearch【保姆级教程、内含图解】_docker elasticsearch_Acloasia的博客-CSDN博客 创建网络 docker network create es-net 基于Docker安装Elasticsearch 拉取镜像 docker pull elasticsearch:8.9.1 挂载文件 mkdir -p /usr/local/e…...

12. Oracle中case when详解
格式: case expression when condition_01 then result_01 when condition_02 then result_02 ...... when condition_n then result_n else result_default end 表达式expression符合条件condition_01,则返回…...

【电路设计】220V AC转低压DC电路概述
前言 最近因项目需要,电路板上要加上一个交流220V转低压直流,比如12V或者5V这种。一般来说,比较常见也比较简单的做法是使用一个变压器将220V AC进行降压,比如降到22V AC,但是很遗憾的是,支持220V的变压器一般体积很大,而板子留给电源部分的面积又非常有限,所以不得不研…...
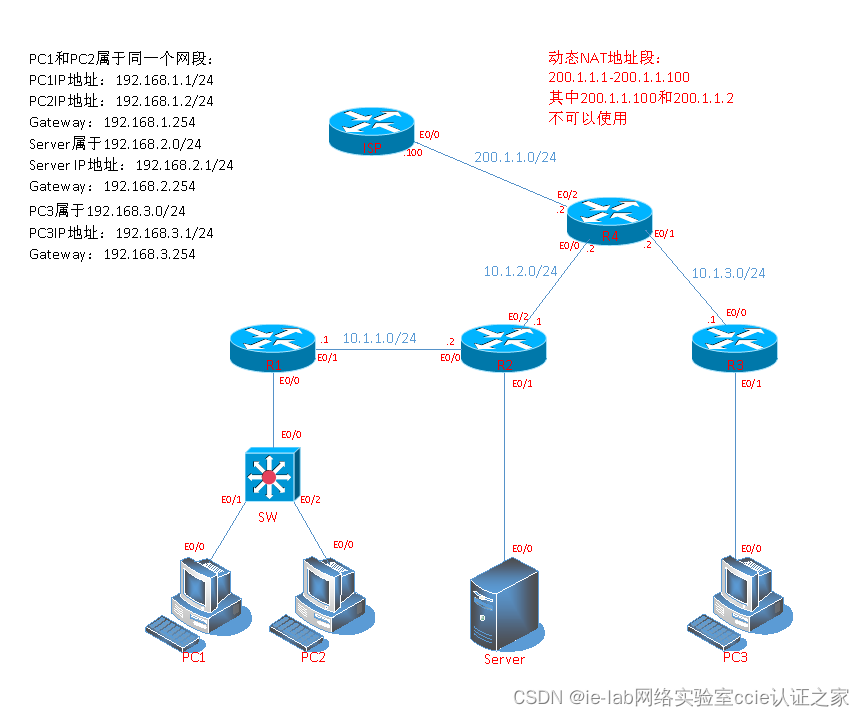
网络地址转换NAT-动态NAT的使用范围和配置-思科EI,华为数通
网络地址转换NAT-动态NAT的使用范围和配置 什么是动态NAT? 使用公有地址池,并以先到先得的原则分配这些地址。当具有私有 IP 地址的主机请求访问 Internet 时,动态 NAT 从地址池中选择一个未被其它主机占用的 IP 地址一对一的转化。当数据会话…...
远程连接虚拟机中ubuntu报错:Network error:Connection refused
ping检测一下虚拟机 可以ping通,说明主机是没问题 #检查ssh是否安装: ps -e |grep ssh发现ssh没有安装 #安装openssh-server sudo apt-get install openssh-server#启动ssh service ssh startps -e |grep ssh检查一下防火墙 #防火墙状态查看 sudo ufw…...
快速排序三种思路详解!
一、快速排序的介绍 快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中 的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,…...

【二叉树入门指南】链式结构的实现
【二叉树入门指南】链式结构的实现 一、前置说明二、二叉树的遍历2.1前序遍历2.2中序遍历2.3 后序遍历 三、以前序遍历为例,递归图解四、层序遍历五、节点个数以及高度等5.1 二叉树节点个数5.2二叉树叶子节点个数5.3 二叉树第k层节点个数5.4 二叉树查找值为x的节点5…...
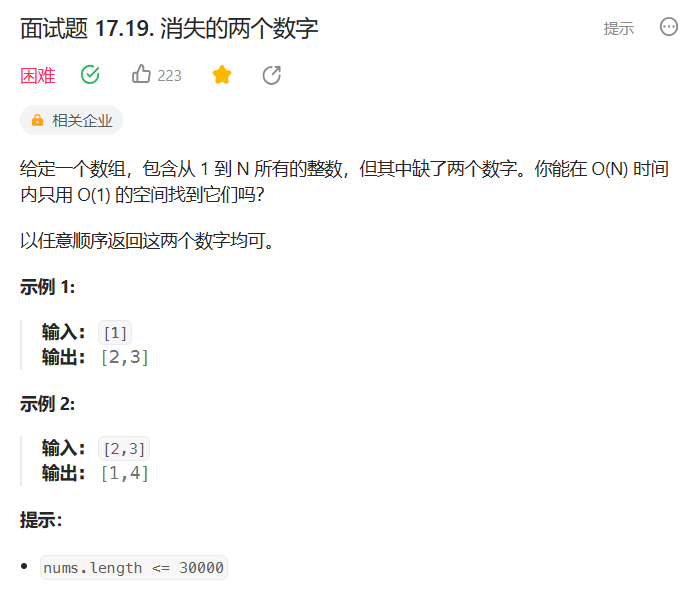
【位运算】算法实战
文章目录 一、算法原理常见的位运算总结 二、算法实战1. leetcode面试题01.01. 判断字符是否唯一2. leetcode268 丢失的数字3. leetcode371 两整数之和4. leetcode004 只出现一次的数字II5. leetcode面试题17.19. 消失的两个数字 三、总结 一、算法原理 计算机中的数据都以二进…...

C++构建系统
收集C构建系统(2023): 跟我一起写Makefile (PDF重制版)CMake tutorialConan, software package manager for C and C developersvcpkg-repovcpkgGoogle Bazel Build System { Fast, Correct } — Choose twoGN gn_quick_start当前Chromium构建系统 GYP Generate You…...

“深入探索JVM内部机制:理解Java虚拟机的运行原理“
标题:深入探索JVM内部机制:理解Java虚拟机的运行原理 摘要:本篇博客将深入探索Java虚拟机(JVM)的内部机制,帮助读者理解JVM的运行原理。我们将介绍JVM的组成结构,包括类加载器、运行时数据区域…...

java八股文面试[JVM]——双亲委派模型
1.当AppClassLoader去加载一个class时,它首先不会自己去尝试加载这个类,而是把类加载请求委托给父加载器ExtClassLoader去完成。 2.当ExtClassLoader去加载一个class时,它首先也不会去尝试加载这个类,而是把类加载请求委托给父加载…...

NLP与大模型主题全国师资培训班落地,飞桨持续赋能AI人才培养
为了推动大模型及人工智能相关专业人员的培养,8月11日-8月13日,由中国计算机学会主办、机械工业出版社、北京航空航天大学、百度飞桨联合承办 “CCF群星计划之文心高校行- NLP与大模型”主题师资培训班(以下简称培训班)在北京天信…...

Jupyter Notebook 配置根目录
注:本文是在 Windows 10 上配置 Jupyter Notebook 打开的默认根目录,Linux 同。 步骤一:创建 Jupyter Notebook 配置文件 使用以下命令创建 Jupyter Notebook 配置文件(如果尚未创建): jupyter notebook …...

算法 位运算
文章目录 一、&(按位与)运算符二、|(按位或)运算符三、^(异或)运算符四、~(取反)运算符五、<<(左移)运算符六、>>(右移ÿ…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

HTTPS证书一年多少钱?
HTTPS证书作为保障网站数据传输安全的重要工具,成为众多网站运营者的必备选择。然而,面对市场上种类繁多的HTTPS证书,其一年费用究竟是多少,又受哪些因素影响呢? 首先,HTTPS证书通常在PinTrust这样的专业平…...
