编码基础一:侵入式链表
一、简介概述
1、普通链表数据结构

每个节点的next指针指向下一个节点的首地址。这样会有如下的限制:
- 一条链表上的所有节点的数据类型需要完全一致。
- 对某条链表的操作如插入,删除等只能对这种类型的链表进行操作,如果链表的类型换了,就要重新再封装出一套一样的操作,泛化能力差
2、侵入式链表数据结构

节点的链接成员指向的是下一个节点的链接成员。使用侵入式链表的好处是:
- 节点类型无需一致,只需要成员节点(element_t)包含list_node_t成员即可
- 泛化能力强,所有链表的操作方式均可统一;
typedef struct list_node list_node_t;//链表节点结构体定义
typedef struct list_node {list_node_t* prev;list_node_t* next;
} list_node_t;//链表结构体定义
typedef struct list {int list_size;list_node_t head;
} list_t;//链表成员结构体定义,重点需要包含list_node_t定义
typedef struct element {list_node_t list_node;int element_type;int element_size;char element_data[1];
} element_t;二、详细介绍
侵入式链表中的节点只有地址信息,能够访问节点上的数据成员变量,主要靠两个核心函数:
- offsetof
- container_of
1、offsetof
1)宏原型
#if defined _MSC_VER && !defined _CRT_USE_BUILTIN_OFFSETOF#ifdef __cplusplus#define offsetof(s,m) \((::size_t)&reinterpret_cast<char const volatile&>((((s*)0)->m)))#else#define offsetof(s,m) ((size_t)&(((s*)0)->m))#endif
#else#define offsetof(s,m) __builtin_offsetof(s,m)
#endif2)宏作用
计算结构体成员相对于结构体的偏移
3)参数说明
- type: 结构体类型
- member:结构体成员
4)原理分析
偏移 = 成员地址 - 结构体地址,若结构体地址为0,则偏移 = 成员地址;
5)应用示例
typedef struct element {list_node_t list_node;int element_type;int element_size;char element_data[1];
} element_t;printf("offset: %zd %zd %zd\r\n", offsetof(element_t, list_node), offsetof(element_t, element_type), offsetof(element_t, element_size));//打印结果
offset: 0 16 202、container_of
1)宏原型
#define container_of(ptr, type, member) \((type*)(((char*)((type*)(ptr))) - offsetof(type, member)))2)宏作用
通过结构体的成员,结构体成员的地址以及结构体的类型来获取结构体的首地址。
3)参数说明
- ptr: 结构体成员的地址
- type: 结构体类型
- member:结构体成员
4)原理分析
结构体首地址 = 成员地址 - 成员偏移,成员偏移通过offsetof宏求出;
5)应用示例
int main()
{element_t element, *p_element;element.element_type = 1234;element.element_size = 5678;p_element = container_of(&element.list_node, element_t, list_node);printf("p_element->element_type :%d p_element->element_size :%d\n", p_element->element_type, p_element->element_size);
}p_element->element_type :1234 p_element->element_size :56783、侵入式链表
介绍到这里,就可以理解面前第一章第2小节,介绍的节点类型无需一致,只需要成员节点(element_t)包含list_node_t成员即可。我们只要知道list_node_t成员地址,就可以通过offsetof=>container_of获取整个element_t的成员变量。
示例代码如下:
#include "list.h"
#include <assert.h>
#include <stdio.h>
#include <stdlib.h>
#include <windows.h>void ListInit(list_t* list) {list->list_size = 0;ListNodeInit(&list->head);
}void ListAppend(list_t* list, list_node_t* node) {node->next = &list->head;node->prev = list->head.prev;node->prev->next = node;list->head.prev = node;list->list_size++;
}void ListRemove(list_t* list, list_node_t* node) {ListNodeDetach(node);ListNodeInit(node);list->list_size--;
}list_node_t* ListFirstGet(const list_t* list) {return !ListEmpty(list) ? list->head.next : NULL;
}list_node_t* ListLastGet(const list_t* list) {return !ListEmpty(list) ? list->head.prev : NULL;
}bool ListEmpty(const list_t* list) {return !ListEnlisted(&list->head);
}void ListNodeInit(list_node_t* node) {node->prev = node;node->next = node;
}void ListNodeDetach(list_node_t* node) {node->prev->next = node->next;node->next->prev = node->prev;
}bool ListEnlisted(const list_node_t* node) {return node->prev != node;
}list_t list_;int main()
{list_node_t* list_node = NULL;ListInit(&list_);for (int i = 0; i < 15; i++) {element_t* element = (element_t*)malloc(sizeof(element_t) + sizeof(AI_UPLOAD_ALL_INFO_T));element->element_type = i;element->element_size = sizeof(AI_UPLOAD_ALL_INFO_T);ListAppend(&list_, &element->list_node);printf("push element :%d queue_size :%d\n", element->element_type, list_.list_size);list_node = ListLastGet(&list_);element_t* element1 = GetListNode(list_node, element_t);printf("QueueLastGet element :%d queue_size :%d\n", element1->element_type, list_.list_size);}printf("list_size :%d\n", list_.list_size);while ((list_node = ListFirstGet(&list_)) != NULL) {element_t* element = GetListNode(list_node, element_t);printf("pop element :%d queue_size :%d\n", element->element_type, list_.list_size);ListRemove(&list_, list_node);}return 0;
}相关文章:

编码基础一:侵入式链表
一、简介概述 1、普通链表数据结构 每个节点的next指针指向下一个节点的首地址。这样会有如下的限制: 一条链表上的所有节点的数据类型需要完全一致。对某条链表的操作如插入,删除等只能对这种类型的链表进行操作,如果链表的类型换了&#…...

深圳IT行业供需:蓬勃发展的科技中心
深圳作为中国的科技中心之一,IT行业在这座城市蓬勃发展。本文将探讨深圳IT行业的供需状况,包括就业机会、技能需求以及行业前景展望。 近年来,深圳IT行业迅速发展,成为全球科技创新的重要枢纽之一。随着大量的科技企业和初创公司在…...

LeetCode 面试题 02.01. 移除重复节点
文章目录 一、题目二、C# 题解 一、题目 编写代码,移除未排序链表中的重复节点。保留最开始出现的节点。 点击此处跳转题目。 示例1: 输入:[1, 2, 3, 3, 2, 1] 输出:[1, 2, 3] 示例2: 输入:[1, 1, 1, 1, 2] 输出:[1, …...

【Java8特性】——Stream API
一、概述 <1> 是什么 是数据渠道,用于操作数据源(集合、数组等)所生成的元素序列。 Stream 不会存储数据Stream 不会改变数据源,相反,会返回一个持有结果的新Stream。Stream 操作是延迟执行的,这意…...

grep命令的用法
文章目录 前言一、使用说明二、应用举例 前言 grep 命令用于查找文件里符合条件的字符串。 一、使用说明 -r: 如果需要搜索目录中的文件内容, 需要进行递归操作, 必须指定该参数 -i: 对应要搜索的关键字, 忽略字符大小写的差别 -n: 在显示符合样式的那一行之前,标…...
【无标题】jenkins消息模板(飞书)
这里写目录标题 Jenkins 安装的插件 发送消息到飞书预览 1 (单Job)预览 2 (多Job,概览) Jenkins 安装的插件 插件名称作用Rebuilder Rebuilder。 官方地址:https://plugins.jenkins.io/rebuild 安装方式&a…...

2023年国赛 高教社杯数学建模思路 - 案例:随机森林
文章目录 1 什么是随机森林?2 随机深林构造流程3 随机森林的优缺点3.1 优点3.2 缺点 4 随机深林算法实现 建模资料 ## 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 什么是随机森林ÿ…...

element Collapse 折叠面板 绑定事件
1. 点击面板触发事件 change <el-collapse accordion v-model"activeNames" change"handleChange"><el-collapse-item title"一致性 Consistency"><div>与现实生活一致:与现实生活的流程、逻辑保持一致,…...

CSS :mix-blend-mode、aspect-ratio
mix-blend-mode 元素的内容应该与元素的直系父元素的内容和元素的背景如何混合。 mix-blend-mode: normal; // 正常mix-blend-mode: multiply; // 正片叠底mix-blend-mode: screen; // 滤色mix-blend-mode: overlay; // 叠加mix-blend-mode: darken; // 变暗mix-blend-mode: …...
Module not found: Error: Can‘t resolve ‘less-loader‘解决办法
前言: 主要是在自我提升方面,感觉自己做后端还是需要继续努力,争取炮筒前后端,作为一个全栈软阿金开发人员,所以还是需要努力下,找个方面,目前是计划学会Vue,这样后端有java和pytho…...

量化QAT QLoRA GPTQ
模型量化的思路可以分为PTQ(Post-Training Quantization,训练后量化)和QAT(Quantization Aware Training,在量化过程中进行梯度反传更新权重,例如QLoRA),GPTQ是一种PTQ的思路。 QAT…...

CentOS下查看 ssd 寿命
SSD写入量达到设计极限,颗粒擦写寿命耗尽后会导致磁盘写入速度非常缓慢,读取正常。 使用smartctl及raid卡管理软件查看硬盘smart信息可以发现Media_Wearout_Indicator值降为1,表明寿命完全耗尽。 涉及范围 所有SSD处理方案 查看SSD smart信…...

Node基础--npm相关内容
下面,我们一起来看看Node中的至关重要的一个知识点-----npm 1.npm概述 npm(Node Package Manager),CommonJS包规范是理论,npm是其中一种实践。 对于Node而言,NPM帮助其完成了第三方模块的发布、安装和依赖等。借助npm,Node与第三方模块之间形成了很好的一个 生态系统。(类…...

Python图片爬虫工具
不废话了,直接上代码: import re import os import requests import tqdmheader{User-Agent: Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/66.0.3359.139 Safari/537.36}def getImg(url,idx,path):imgre…...

制造执行系统(MES)在汽车行业中的应用
汽车行业在不断发展中仍然面临一些挑战和痛点。以下是一些当前汽车行业可能面临的问题: 1.电动化和可持续性转型:汽车行业正逐渐向电动化和可持续性转型,但这需要投入大量资金和资源,包括电池技术、充电基础设施等,同时…...

Spring与Mybatis集成且Aop整合
目录 一、集成 1.1 集成的概述 1.2 集成的优点 1.3 代码示例 二、整合 2.1 整合概述 2.2 整合进行分页 一、集成 1.1 集成的概述 集成是指将不同的组件、部分或系统组合在一起,以形成一个整体功能完整的解决方案。它是通过连接、交互和协调组件之间的关系来实…...

【nonebot-plugin-mystool】快速安装使用nonebot-plugin-mystool
快速安装使用nonebot-plugin-mystool,以qq为主 前期准备:注册一个QQ号,python3.9以上的版本安装,go-cqhttp下载 用管理员模式打开powershell,并输入以下命令 #先排查是否有安装过的nonebot,若有则删除 pip uninstal…...
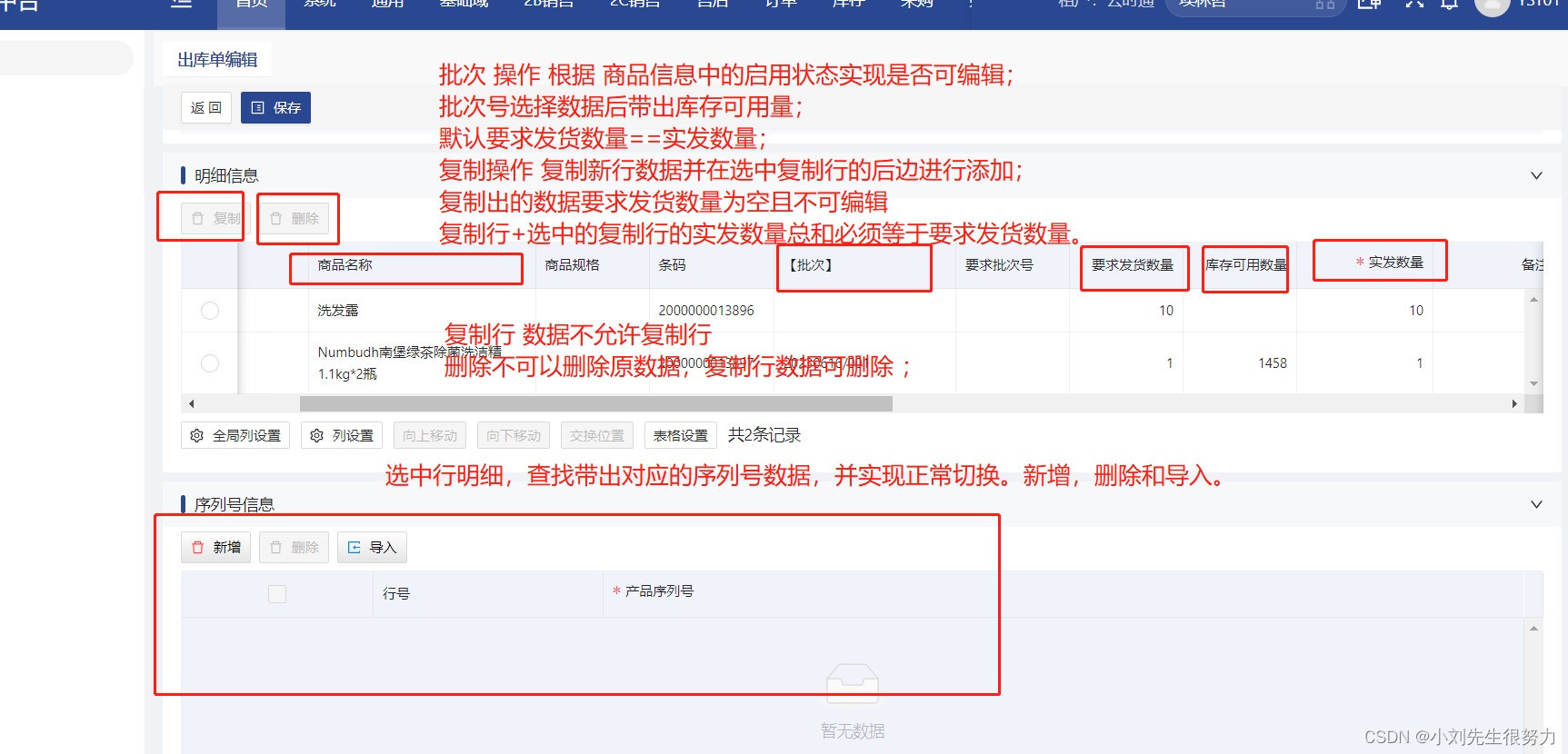
js实现数据关联查找更新。数据求和验证
为了实现这个功能我们和后端定义了数据结构 data:{id:‘’,formInfo:,formInfo2:,formInfo3:,formInfo4:, ......deailData:[ // 明细数据 // saleData 查询带出的对应明细序列号数据{ id:, ocopyId:, copyId:, odoId:, ......, saleData:[ { id:, oc…...

区块链上地址与银行账户有什么区别?
在区块链世界中,除了交易还有另一个基础要素:地址。在日前推出的Onchain AML合规技术方案,也有一个与区块链地址密切相关的概念:KYA(Know Your Address,了解你的地址)。 那问题来了,区块链地址究竟有什么用…...
)
CF 148 D Bag of mice(概率dp求概率)
CF 148 D. Bag of mice(概率dp求概率) Problem - 148D - Codeforces 大意:袋子里有 w 只白鼠和 b 只黑鼠 ,A和B轮流从袋子里抓,谁先抓到白色谁就赢。A每次随机抓一只,B每次随机抓完一只之后会有另一只随机老鼠跑出来。如果两个人…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...
