机器学习之决策树原理详解、公式推导(手推)、面试问题、简单实例(python实现,sklearn调包)

目录
- 1. 决策树原理
- 1.1. 特性
- 1.2. 思路
- 1.3. 概念
- 决策树概念
- 信息论
- 2. 公式推导
- 2.1. 构造决策树
- 2.1.1. ID3
- 理论
- 示例
- 缺点
- 2.1.2. C4.5
- 理论
- 示例
- 缺点
- 2.1.3. CART
- 示例
- 对比分析
- 2.2. 剪枝
- 3. 实例
- 3.1. 数据集
- 3.2. ID3
- 3.3. C4.5
- 3.4. CART
- 3.5. sklearn实现
- 4. 几个注意点(面试问题)
- 5. 运行(可直接食用)
1. 决策树原理
1.1. 特性
决策树属于非参数监督学习方法,在学习数据特征推断出简单的决策规划创建一个预测目标变量值的模型。
优点
- 可解释型强,而且决策树很容易可视化。此外,决策树使用“白箱模型”,比起黑箱模型,解释性也更强。
- 能处理多输出问题。
- 即使其假设与生成数据的真实模型有一定程度的违背,也能很好地执行。
- 使用树(即预测数据)的成本在用于训练树的数据点的数量上是对数的。
缺点
- 很容易就过拟合了。所以才需要剪枝等技巧或者设置叶节点所需最小样本树或者设置树最大深度。
- 不稳定,因为时递归出来的,很微小的变化可能导致整个树结构大变。
- 不擅长泛化和外推。因为决策树的预测不是平滑的也不是连续的,所以中间的空挡很难处理,所以在外推方面表现差。
- 决策树基于的启发式算法可能会导致产生的决策树并非最优决策树,比如在使用贪心算法的时候。因此才会有人提出特征和样本需要被随机抽样替换。
- 在一些问题上先天不足。如:XOR、奇偶校验或多路复用器问题。
- 不支持缺失值,这点在随机森林中也有所提现,所以采取本方法时注意缺失值处理或填补。
1.2. 思路
在计算机中,决策树更多的时用于分类。有点类似于用 if else 语句去穷举每一种可能,但是面对多个判断的情况时,每个判断出现的位置还不确定,我们需要通过某种方法确定各个条件出现顺序(谁在树根谁在下面),这个方法是决策树的一个难点。此外,面对大量数据时,建立的决策树模型可能会特别特别大,深度深,叶子节点多且节点中的样例少等可能性,优化这个问题需要的方法也是一个难题。
所有的决策树的步骤的最终目的都是希望通过学习产生一个泛化能力强的决策树,即处理未见示例能力强的决策树。
1.3. 概念
决策树概念
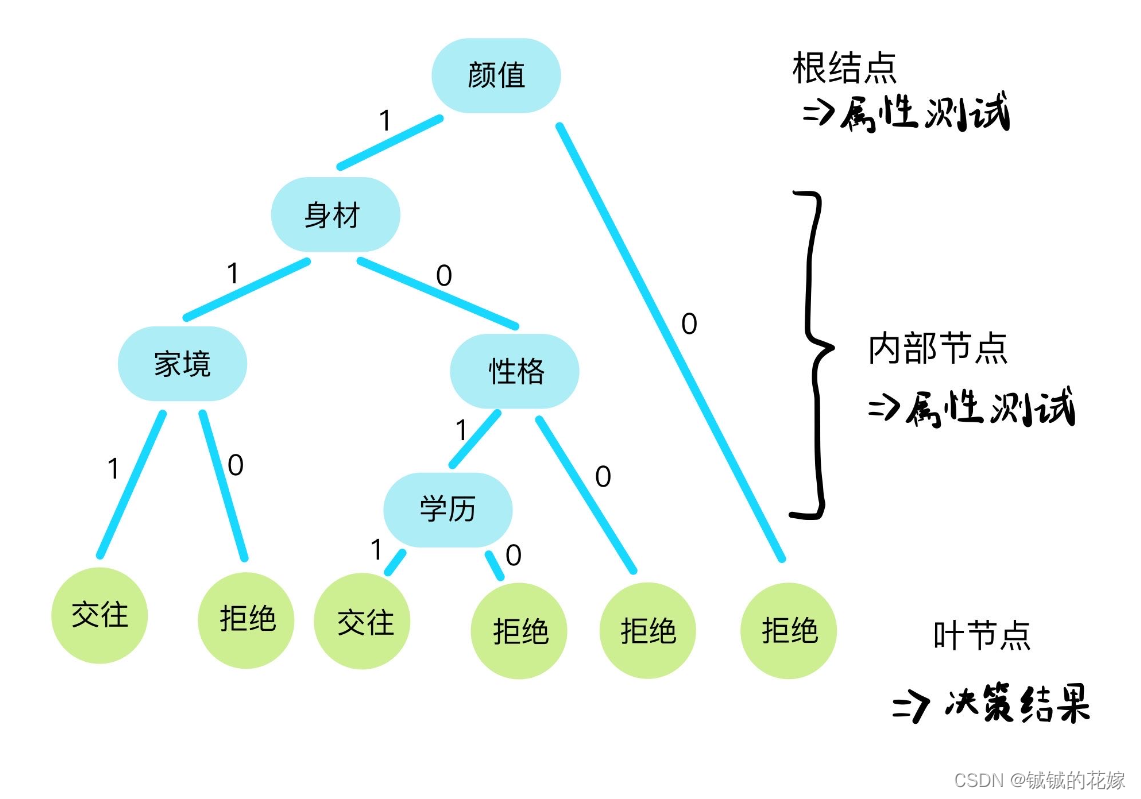
根据西瓜书的定义:⼀棵决策树包含⼀个根节点,若⼲个内部节点和若⼲个叶⼦节点。叶结点对应决策树决策结果,其他每个结点则对应于⼀个属性测试。
信息论
决策树这里用到了信息论中间很基础的知识,我们希望决策树的分支节点所包含的样本尽可能都属于一个类别,那么这么衡量这个?这需要用到纯度。直观上讲就是分类纯度越低,里面的标签就越杂 。
那么纯度怎么表示?
可以用信息熵表示。假定当前样本集合 D 中第 k 类样本所占的比例为 PkP_kPk (k =1, 2,. . . ,∣γ∣|\gamma|∣γ∣) ,则D的信息熵定义为:
Ent(D)=−∑k=1∣γ∣pklog2pkEnt(D)=-\sum^{|\gamma|}_{k=1}{p_klog_2p_k} Ent(D)=−k=1∑∣γ∣pklog2pk
Ent(D)的值越小,则D的纯度越⾼。
Ent(D)的值越大,则D的不纯度越大,则D的不确定性越大。
2. 公式推导
决策树模型构建一般分为三步,
- 特征选择
- 决策树生成
- 决策树修剪
特征选择更多的是取决于数据集,在生活中的问题里可能更加重要,一般来说没有什么特定的标准,需要注意的点比较琐碎,这边不细讲。
决策树生成和修剪的难度更大,这里做出总结。
2.1. 构造决策树
如何构造决策树其实就是如何选取每层节点的问题,西瓜书上介绍了三种方法,这边也按照这三种方法总结,其他的方法我将在面试题中提到。
2.1.1. ID3
理论
靠信息增益区分。
我们知道信息熵可以确定经过一个节点划分后每个分支节点的纯度,但是我们这里需要确定节点的顺序,所以单单知道划分后每个分支节点的纯度还不够,应该通过某种方法利用分支节点的纯度反映到划分节点的优劣。
ID3就是使用信息增益来判断每个节点的划分能力的。信息增益公式如下:
Gain(D,α)=Ent(D)−∑v=1V∣Dv∣∣D∣Ent(Dv)Gain(D, \alpha)=Ent(D)-\sum^{V}_{v=1}{\frac{|D^v|}{|D|}Ent(D^v)} Gain(D,α)=Ent(D)−v=1∑V∣D∣∣Dv∣Ent(Dv)
∣Dv∣∣D∣\frac{|D^v|}{|D|}∣D∣∣Dv∣就是每个分支节点的划分权重,所以样本数量越多划分权重越大。Gain(D,α)Gain(D, \alpha)Gain(D,α)就是使用α\alphaα属性划分对整体纯度提升的能力。因此我们有 ID3 的逻辑顺序:
- 从根节点开始,会节点计算所有可能的特征的信息增益,选择信息增益最大的特征作为节点的特征。
- 由该特征的不同取值建立子节点,在对子节点递归地调用上面方法,构建决策树,知道所有的特征信息增益都很小或者没有特征可以选为止。
- 得到决策树模型。
示例
西瓜数据集
| 编号 | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 密度 | 含糖率 | 好瓜 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.697 | 0.46 | 1 |
| 2 | 1 | 0 | 1 | 0 | 0 | 0 | 0.774 | 0.376 | 1 |
| 3 | 1 | 0 | 0 | 0 | 0 | 0 | 0.634 | 0.264 | 1 |
| 4 | 0 | 0 | 1 | 0 | 0 | 0 | 0.608 | 0.318 | 1 |
| 5 | 2 | 0 | 0 | 0 | 0 | 0 | 0.556 | 0.215 | 1 |
| 6 | 0 | 1 | 0 | 0 | 1 | 1 | 0.403 | 0.237 | 1 |
| 7 | 1 | 1 | 0 | 1 | 1 | 1 | 0.481 | 0.149 | 1 |
| 8 | 1 | 1 | 0 | 0 | 1 | 0 | 0.437 | 0.211 | 1 |
| 9 | 1 | 1 | 1 | 1 | 1 | 0 | 0.666 | 0.091 | 0 |
| 10 | 0 | 2 | 2 | 0 | 2 | 1 | 0.243 | 0.267 | 0 |
| 11 | 2 | 2 | 2 | 2 | 2 | 0 | 0.245 | 0.057 | 0 |
| 12 | 2 | 0 | 0 | 2 | 2 | 1 | 0.343 | 0.099 | 0 |
| 13 | 0 | 1 | 0 | 1 | 0 | 0 | 0.639 | 0.161 | 0 |
| 14 | 2 | 1 | 1 | 1 | 0 | 0 | 0.657 | 0.198 | 0 |
| 15 | 1 | 1 | 0 | 0 | 1 | 1 | 0.36 | 0.37 | 0 |
| 16 | 2 | 0 | 0 | 2 | 2 | 0 | 0.593 | 0.042 | 0 |
| 17 | 0 | 0 | 1 | 1 | 1 | 0 | 0.719 | 0.103 | 0 |
计算根蒂的信息增益:

缺点
对种类多的属性有偏好,比如编号属性。这个属性的信息增益会特别高,但是实际上它所包含的信息没多少。
此时就需要另一个算法 C4.5
2.1.2. C4.5
理论
靠增益率区分。
既然考虑到信息增益对种类多的属性的偏好,增益率应该削弱这类属性的权重。于是提出增益的权重,也称为属性的固有值。
对信息增益提出了惩罚,特征可取值数量较多时,惩罚参数大;特征可取值数量较少时,惩罚参数小。
IV(α)=−∑v=1V∣Dv∣∣D∣log2∣Dv∣∣D∣IV(\alpha)=-\sum^{V}_{v=1}{\frac{|D^v|}{|D|}}log_2\frac{|D^v|}{|D|} IV(α)=−v=1∑V∣D∣∣Dv∣log2∣D∣∣Dv∣
Gain_ratio=Gain(D,α)IV(α)Gain\_ratio=\frac{Gain(D,\alpha)}{IV(\alpha)} Gain_ratio=IV(α)Gain(D,α)
底层思路是讲连续特征离散化,所有也可以用来处理连续型数据。
示例
西瓜数据集
| 编号 | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 密度 | 含糖率 | 好瓜 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.697 | 0.46 | 1 |
| 2 | 1 | 0 | 1 | 0 | 0 | 0 | 0.774 | 0.376 | 1 |
| 3 | 1 | 0 | 0 | 0 | 0 | 0 | 0.634 | 0.264 | 1 |
| 4 | 0 | 0 | 1 | 0 | 0 | 0 | 0.608 | 0.318 | 1 |
| 5 | 2 | 0 | 0 | 0 | 0 | 0 | 0.556 | 0.215 | 1 |
| 6 | 0 | 1 | 0 | 0 | 1 | 1 | 0.403 | 0.237 | 1 |
| 7 | 1 | 1 | 0 | 1 | 1 | 1 | 0.481 | 0.149 | 1 |
| 8 | 1 | 1 | 0 | 0 | 1 | 0 | 0.437 | 0.211 | 1 |
| 9 | 1 | 1 | 1 | 1 | 1 | 0 | 0.666 | 0.091 | 0 |
| 10 | 0 | 2 | 2 | 0 | 2 | 1 | 0.243 | 0.267 | 0 |
| 11 | 2 | 2 | 2 | 2 | 2 | 0 | 0.245 | 0.057 | 0 |
| 12 | 2 | 0 | 0 | 2 | 2 | 1 | 0.343 | 0.099 | 0 |
| 13 | 0 | 1 | 0 | 1 | 0 | 0 | 0.639 | 0.161 | 0 |
| 14 | 2 | 1 | 1 | 1 | 0 | 0 | 0.657 | 0.198 | 0 |
| 15 | 1 | 1 | 0 | 0 | 1 | 1 | 0.36 | 0.37 | 0 |
| 16 | 2 | 0 | 0 | 2 | 2 | 0 | 0.593 | 0.042 | 0 |
| 17 | 0 | 0 | 1 | 1 | 1 | 0 | 0.719 | 0.103 | 0 |
计算根蒂的信息增益率:

缺点
缺点也很明显,就是矫枉过正。面对可取数值比较少的属性时,增益率存在偏好。因此有了基指系数。
2.1.3. CART
靠基尼指数划分。
我们可以理解为随机抽取两个样本,其类别不一样的概率的加权和。这个权重跟 C4.5 的权重划分方法相同。
这个本质上是一个回归树,对于计算机来说虽然很多时候结果跟信息熵算出来的差不多,但是计算会快很多,因为没有对数。
数据集的基尼指数:
Gini(D)=∑k=1∣γ∣∑k′≠kpkpk′=1−∑k=1∣γ∣pk2=1−∑k=1∣γ∣(∣Di∣∣D∣)2Gini(D)=\sum^{|\gamma|}_{k=1}\sum_{k^{'} \ne k}p_kp_{k^{'}}=1-\sum^{|\gamma|}_{k=1}p_{k}^{2}=1-\sum^{|\gamma|}_{k=1}{(\frac{|D_i|}{|D|})^2} Gini(D)=k=1∑∣γ∣k′=k∑pkpk′=1−k=1∑∣γ∣pk2=1−k=1∑∣γ∣(∣D∣∣Di∣)2
数据集纯度越高,∑k=1∣γ∣pk2\sum^{|\gamma|}_{k=1}p_{k}^{2}∑k=1∣γ∣pk2 越大,Gini 越小。
属性的基尼指数:
Gini_index(D,α)=∑v=1V∣Dv∣∣D∣Gini(Dv)Gini\_index(D, \alpha )=\sum^{V}_{v=1}{\frac{|D^v|}{|D|}Gini(D^{v})} Gini_index(D,α)=v=1∑V∣D∣∣Dv∣Gini(Dv)
最优划分属性就是 Gini_index(D,α)Gini\_index(D, \alpha )Gini_index(D,α) 最小的属性。
示例
西瓜数据集
| 编号 | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 密度 | 含糖率 | 好瓜 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.697 | 0.46 | 1 |
| 2 | 1 | 0 | 1 | 0 | 0 | 0 | 0.774 | 0.376 | 1 |
| 3 | 1 | 0 | 0 | 0 | 0 | 0 | 0.634 | 0.264 | 1 |
| 4 | 0 | 0 | 1 | 0 | 0 | 0 | 0.608 | 0.318 | 1 |
| 5 | 2 | 0 | 0 | 0 | 0 | 0 | 0.556 | 0.215 | 1 |
| 6 | 0 | 1 | 0 | 0 | 1 | 1 | 0.403 | 0.237 | 1 |
| 7 | 1 | 1 | 0 | 1 | 1 | 1 | 0.481 | 0.149 | 1 |
| 8 | 1 | 1 | 0 | 0 | 1 | 0 | 0.437 | 0.211 | 1 |
| 9 | 1 | 1 | 1 | 1 | 1 | 0 | 0.666 | 0.091 | 0 |
| 10 | 0 | 2 | 2 | 0 | 2 | 1 | 0.243 | 0.267 | 0 |
| 11 | 2 | 2 | 2 | 2 | 2 | 0 | 0.245 | 0.057 | 0 |
| 12 | 2 | 0 | 0 | 2 | 2 | 1 | 0.343 | 0.099 | 0 |
| 13 | 0 | 1 | 0 | 1 | 0 | 0 | 0.639 | 0.161 | 0 |
| 14 | 2 | 1 | 1 | 1 | 0 | 0 | 0.657 | 0.198 | 0 |
| 15 | 1 | 1 | 0 | 0 | 1 | 1 | 0.36 | 0.37 | 0 |
| 16 | 2 | 0 | 0 | 2 | 2 | 0 | 0.593 | 0.042 | 0 |
| 17 | 0 | 0 | 1 | 1 | 1 | 0 | 0.719 | 0.103 | 0 |
计算根蒂的基尼指数:

对比分析
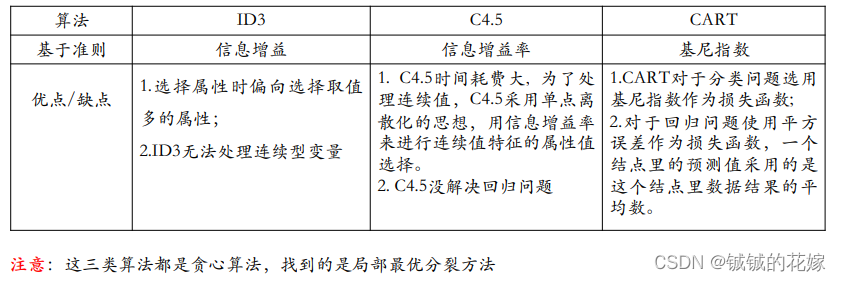
2.2. 剪枝
剪枝 (pruning)是决策树学习算法对付"过拟合"的主要⼿段。在决策树学习中,为了尽可能正确分类训练样本,结点划分过程将不断重复,有时会造成决策树分支过多,这时就可能因训练样本学得"太好"了,以致于把训练集自身的⼀些特点当作所有数据都具有的⼀般性质⽽导致过拟合。
决策树剪枝的基本策略有“预剪枝” (prepruning)和“后剪枝 ”(post pruning) [Quinlan, 1993]. 预剪枝是指在决策树⽣成过程中,对每个结点在划分前先进⾏估计,若当前结点的划分不能带来决策树泛化性能提升,则停⽌划分并将当前结点标记为叶结点;后剪枝则是先从训练集⽣成⼀棵完整的决策树, 然后自底向上地对非叶结点进⾏考察,若将该结点对应的⼦树替换为叶结点能带来决策树泛化性能提升,则将该⼦树替换为叶结点。
3. 实例
3.1. 数据集
watermelon.csv
x1,x2,x3,x4,x5,x6,label
0,0,0,0,0,0,1
1,0,1,0,0,0,1
1,0,0,0,0,0,1
0,0,1,0,0,0,1
2,0,0,0,0,0,1
0,1,0,0,1,1,1
1,1,0,1,1,1,1
1,1,0,0,1,0,1
1,1,1,1,1,0,0
0,2,2,0,2,1,0
2,2,2,2,2,0,0
2,0,0,2,2,1,0
0,1,0,1,0,0,0
2,1,1,1,0,0,0
1,1,0,0,1,1,0
2,0,0,2,2,0,0
0,0,1,1,1,0,0
3.2. ID3
# 计算信息熵
def c_entropy(label):# 每类有几个count_class = Counter(label)ret = 0for classes in count_class.keys():ret += count_class[classes]/len(label)*np.log2(count_class[classes]/len(label))return -ret# 计算单个属性信息增益
def c_entropy_gain(data, label):ent = c_entropy(label)# 几个值循环几次count_value = Counter(data)sum_entropy = 0for value_a in count_value.keys():sum_entropy += count_value[value_a] / len(label) * c_entropy(label[data == value_a])return ent - sum_entropy# 计算计算每个属性的信息增益并求最大的
def find_entropy_index(data, label):label = label.flatten()feature_count = data.shape[1]max_list = []for i in range(feature_count):max_list.append(c_entropy_gain(data[:, i], label))max_value = max(max_list) # 求列表最大值max_idx = max_list.index(max_value) # 求最大值对应索引return max_idx
3.3. C4.5
# 计算信息熵
def c_entropy(label):# 每类有几个count_class = Counter(label)ret = 0for classes in count_class.keys():ret += count_class[classes]/len(label)*np.log2(count_class[classes]/len(label))return -ret# 计算单个属性信息增益率
def c_entropy_gain_rate(data, label):ent = c_entropy(label)# 几个值循环几次count_value = Counter(data)sum_entropy = 0sum_iv = 0for value_a in count_value.keys():d = count_value[value_a] / len(label)sum_entropy += d * c_entropy(label[data == value_a])sum_iv -= d * np.log2(d)return (ent - sum_entropy) / sum_iv# 计算计算每个属性的信息增益率并求最大的
def find_entropy_ratio(data, label):# 返回大于中位数的下标def get_mid_index(list):mid = int(len(list)/2)b = sorted(enumerate(list), key=lambda x: x[1]) # x[1]是因为在enumerate(a)中,a数值在第1位c = [x[0] for x in b] # 获取排序好后b坐标,下标在第0位return c[mid:]label = label.flatten()feature_count = data.shape[1]max_list_e = []max_list = []for i in range(feature_count):max_list_e.append(c_entropy_gain(data[:, i], label))max_list.append(c_entropy_gain_rate(data[:, i], label))# 只保留信息增益大于平均水平的max_list_mid = [max_list[i] for i in get_mid_index(max_list_e)]max_value = max(max_list_mid) # 求列表最大值max_idx = max_list_mid.index(max_value) # 求最大值对应索引return max_idx
3.4. CART
# 计算单个属性基尼指数
def c_gini(data, label):# 几个值循环几次count_value = Counter(data)gini = 0for value_a in count_value.keys():d = count_value[value_a] / len(label)class_gini = 1# 取出值一样的data的valuesame_value_class = label[data == value_a]count_labels = Counter(same_value_class)for i in count_labels.values():class_gini -= (i / count_value[value_a])**2gini += d * class_ginireturn gini# 计算计算每个属性的基尼指数并求最小的
def find_gini(data, label):label = label.flatten()feature_count = data.shape[1]min_list = []for i in range(feature_count):min_list.append(c_gini(data[:, i], label))min_value = min(min_list) # 求列表最小值min_idx = min_list.index(min_value) # 求最小值对应索引return min_idx
3.5. sklearn实现
def sk(data_train, label_train, data_test, label_test):clf = tree.DecisionTreeClassifier(criterion="entropy")clf = clf.fit(data_train, label_train)score = clf.score(data_test, label_test) # 返回精确度print("准确率为:", score * 100, "%")# 画决策树feature_name = ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感']import matplotlib as mplmpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定中文字体mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题plt.rcParams['font.sans-serif'] = ['SimHei']plt.rcParams['axes.unicode_minus'] = False # 正常显示负号fig, axes = plt.subplots(nrows=1, ncols=1, figsize=(4, 4), dpi=300)tree.plot_tree(clf,feature_names=feature_name,class_names=["好瓜", "坏瓜"],filled=True, # 填充颜色,颜色越深,不纯度越低rounded=True # 框的形状)plt.show()结果如下
可视化一下:
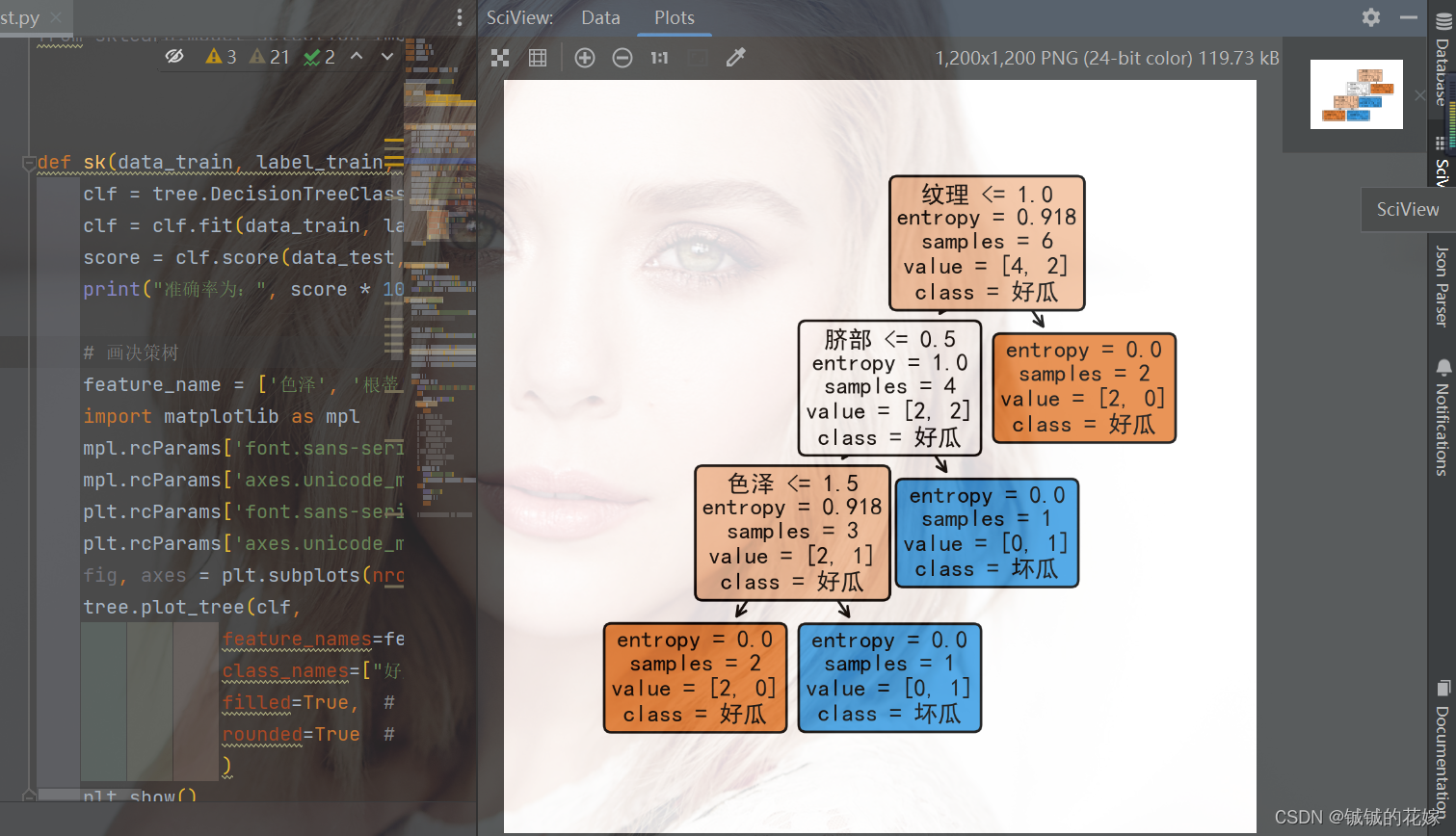
4. 几个注意点(面试问题)
决策树有几个注意点,可能会在面试中被提到,还是比较能体现被面试者对这个算法的理解的。当然我们也不一定就是为了面试,搞清楚这些问题对帮助我们理解这个算法还是很有好处的。其中部分答案是博主自己的理解,如果有问题麻烦路过的大佬评论区指正。
- 决策树常使用那些常用的启发函数?
答:
- ID3 => 最大信息增益
- C4.5 => 最大信息增益比
- CART => 最大基尼指数
这仨还有一些特点:
-
ID3 泛化能力弱,C4.5一定程度上惩罚了取值较多的特征,避免ID3的过拟合,提升泛化能力。
-
ID3 只能处理离散数据,其他俩都可以处理连续型变量,C4.5靠排序后找分割线把连续型变量转化为布尔型,CART靠对特征二值划分。
-
ID3 C4.5 只能做分类任务,CART可以分类也可以回归。
-
ID3 对缺失值特别敏感。
-
ID3 C4.5 每个节点可以产生多分支,CART只会产生二分支。
- 决策树是如何进行剪枝的?
答:
老生常谈的问题了,前面也有讲。这里就重复讲下。
预剪枝
在树长到一定深度后停止生长,当树的节点样本数小于某个阈值时停止生长,每次分裂树带来的提升小于某个阈值时停止生长。
可能导致欠拟合。不过比较适合大规模的问题,在分类后期准确率会有显著增长。需要有经验的人确定相关参数(节点样本数、最大深度等)
后剪枝
后剪枝是在树建立后,从下往上计算是否需要剪掉一部分子树并用叶子代替。比较难的地方是几个后剪枝的方法(错误率降低后剪枝、悲观剪枝、代价复杂度剪枝、最小误差剪枝、CVP、OPP 等)。这个比较复杂,不详细介绍。
- 决策树递归时导致递归返回的三种条件?
答:
- 当前节点包含的样本全部属于统同一类别,无需划分。
- 当前属性集为空,或是所有样本在所有属性上取值相同,无法划分。
- 当前节点包含的样本集合为空,不能划分。
- 计算恋爱数据集。数据集如下:
| 样本 | 颜值(A) | 身材(B) | 性格(C) | 收入(D) | 学历(E) | 交往(R) |
|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 0 | 0 | 0 | 0 |
| 3 | 1 | 1 | 1 | 1 | 1 | 1 |
| 4 | 1 | 0 | 1 | 0 | 1 | 0 |
| 5 | 1 | 1 | 0 | 1 | 0 | 0 |
| 6 | 0 | 1 | 0 | 1 | 1 | 0 |
| 7 | 1 | 1 | 0 | 0 | 0 | 0 |
| 8 | 1 | 0 | 1 | 1 | 1 | 1 |
| 9 | 0 | 0 | 1 | 1 | 1 | 0 |
| 10 | 1 | 1 | 1 | 1 | 1 | 1 |
| 11 | 1 | 0 | 1 | 0 | 0 | 0 |
| 12 | 0 | 0 | 1 | 1 | 1 | 0 |
| 13 | 1 | 1 | 1 | 0 | 1 | 1 |
| 14 | 1 | 0 | 1 | 1 | 1 | 1 |
| 15 | 1 | 1 | 1 | 1 | 1 | 1 |
答:
暂时就算一个颜值和身材哈~~


5. 运行(可直接食用)
import random
from collections import Counter
import numpy as np
import pandas as pd
import warnings
from matplotlib import pyplot as plt
warnings.filterwarnings("ignore")
from sklearn import treeclass Node(object):def __init__(self, son=None, data=None, label=None, node_label=None):self.son = son # 节点的子节点self.data = data # 节点包含的数据self.label = label # 节点包含的标签self.node_label = node_label # 按照哪个属性分类self.if_leaf = False # 默认不是子节点def build_tree(data, label, choice):mytree = Node()# 全部属于一个类别if np.unique(label.flatten()).shape[0] == 1:mytree.if_leaf = Truemytree.label = label[0]return mytree# 当前属性都属于一个类别if np.unique(data, axis=0).shape[0] == 1:mytree.if_leaf = True# 听天由命,直接选第一个mytree.label = label[0]return mytree# 样本或属性集合是空的if label.shape[0] == 0:mytree.if_leaf = True# 从来没碰到这种情况,默认0mytree.label = 0return mytree# 判断if choice == 1:mytree = Node(data=data, label=label, node_label=find_entropy_index(data, label))if choice == 2:mytree = Node(data=data, label=label, node_label=find_entropy_ratio(data, label))if choice == 3:mytree = Node(data=data, label=label, node_label=find_gini(data, label))mytree.son_label = Counter(data[:, mytree.node_label]).keys()# 递归# for feature_class in Counter(data[:, mytree.node_label]).keys():# print(data[data[:, mytree.node_label] == feature_class], "\n", label[data[:, mytree.node_label] == feature_class],"\n\n")mytree.son = {feature_class: build_tree(data[data[:, mytree.node_label] == feature_class], label[data[:, mytree.node_label] == feature_class], choice) for feature_class in Counter(data[:, mytree.node_label]).keys()}return mytree# 计算信息熵
def c_entropy(label):# 每类有几个count_class = Counter(label)ret = 0for classes in count_class.keys():ret += count_class[classes]/len(label)*np.log2(count_class[classes]/len(label))return -ret# 计算单个属性信息增益
def c_entropy_gain(data, label):ent = c_entropy(label)# 几个值循环几次count_value = Counter(data)sum_entropy = 0for value_a in count_value.keys():sum_entropy += count_value[value_a] / len(label) * c_entropy(label[data == value_a])return ent - sum_entropy# 计算计算每个属性的信息增益并求最大的
def find_entropy_index(data, label):label = label.flatten()feature_count = data.shape[1]max_list = []for i in range(feature_count):max_list.append(c_entropy_gain(data[:, i], label))max_value = max(max_list) # 求列表最大值max_idx = max_list.index(max_value) # 求最大值对应索引return max_idx# 计算单个属性信息增益率
def c_entropy_gain_rate(data, label):ent = c_entropy(label)# 几个值循环几次count_value = Counter(data)sum_entropy = 0sum_iv = 0for value_a in count_value.keys():d = count_value[value_a] / len(label)sum_entropy += d * c_entropy(label[data == value_a])sum_iv -= d * np.log2(d)return (ent - sum_entropy) / sum_iv# 计算计算每个属性的信息增益率并求最大的
def find_entropy_ratio(data, label):# 返回大于中位数的下标def get_mid_index(list):mid = int(len(list)/2)b = sorted(enumerate(list), key=lambda x: x[1]) # x[1]是因为在enumerate(a)中,a数值在第1位c = [x[0] for x in b] # 获取排序好后b坐标,下标在第0位return c[mid:]label = label.flatten()feature_count = data.shape[1]max_list_e = []max_list = []for i in range(feature_count):max_list_e.append(c_entropy_gain(data[:, i], label))max_list.append(c_entropy_gain_rate(data[:, i], label))# 只保留信息增益大于平均水平的max_list_mid = [max_list[i] for i in get_mid_index(max_list_e)]max_value = max(max_list_mid) # 求列表最大值max_idx = max_list_mid.index(max_value) # 求最大值对应索引return max_idx# 计算单个属性基尼指数
def c_gini(data, label):# 几个值循环几次count_value = Counter(data)gini = 0for value_a in count_value.keys():d = count_value[value_a] / len(label)class_gini = 1# 取出值一样的data的valuesame_value_class = label[data == value_a]count_labels = Counter(same_value_class)for i in count_labels.values():class_gini -= (i / count_value[value_a])**2gini += d * class_ginireturn gini# 计算计算每个属性的基尼指数并求最小的
def find_gini(data, label):label = label.flatten()feature_count = data.shape[1]min_list = []for i in range(feature_count):min_list.append(c_gini(data[:, i], label))min_value = min(min_list) # 求列表最小值min_idx = min_list.index(min_value) # 求最小值对应索引return min_idxdef sk(data_train, label_train, data_test, label_test):clf = tree.DecisionTreeClassifier(criterion="entropy")clf = clf.fit(data_train, label_train)score = clf.score(data_test, label_test) # 返回精确度print("准确率为:", score * 100, "%")# 画决策树feature_name = ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感']import matplotlib as mplmpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定中文字体mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题plt.rcParams['font.sans-serif'] = ['SimHei']plt.rcParams['axes.unicode_minus'] = False # 正常显示负号fig, axes = plt.subplots(nrows=1, ncols=1, figsize=(4, 4), dpi=300)tree.plot_tree(clf,feature_names=feature_name,class_names=["好瓜", "坏瓜"],filled=True, # 填充颜色,颜色越深,不纯度越低rounded=True # 框的形状)plt.show()def pridect(data, mytree):# 找下个节点def find_result(mytree, row):# 如果是叶子节点if mytree.if_leaf:return mytree.label# 不是叶子节点就继续找row_the_value = row[mytree.node_label]return find_result(mytree.son[row_the_value], row)ret = np.array([find_result(mytree, row) for row in data])return retdef eveluate(predict, result):correct = 0for i in range(predict.shape[0]):correct += (int(predict[i][0]+0.5) == result[0])print("准确率为:", correct / predict.shape[0] * 100, "%")if __name__ == '__main__':random.seed(1129)data = pd.read_csv("watermelonData.csv").sample(frac=1, random_state=1129)# 因为西瓜数据集每列都是0到2的,所以这里就不进行标准化了labels = data["label"]data_shuffled = np.array(data[data.columns[:-1]])# 划分训练集测试集data_train = data_shuffled[:int(data_shuffled.shape[0]*0.6), :]label_train = np.array(labels[:data_train.shape[0]]).reshape(-1, 1)data_test = data_shuffled[data_train.shape[0]:, :]label_test = np.array(labels[data_train.shape[0]:]).reshape(-1, 1)choice = 0while choice != 5:print("1. ID3求解\n2. C45求解\n3. CART求解\n4. sklearn求解\n5. 退出")try:choice = int(input())except:breakif choice == 1:print("ID3求解中...")mytree = build_tree(data_train, label_train, choice)eveluate(pridect(data_test, mytree), label_test)# find_entropy_index(data_train, label_train)elif choice == 2:print("C45求解中...")mytree = build_tree(data_train, label_train, choice)eveluate(pridect(data_test, mytree), label_test)# find_entropy_ratio(data_train, label_train)elif choice == 3:print("CART求解中...")mytree = build_tree(data_train, label_train, choice)eveluate(pridect(data_test, mytree), label_test)# find_gini(data_train, label_train)elif choice == 4:print('sklearn yyds')sk(data_train, label_train, data_test, label_test)else:print("退出成功")break参考:
吴恩达《机器学习》
sklearn官网
《百面机器学习》
相关文章:

机器学习之决策树原理详解、公式推导(手推)、面试问题、简单实例(python实现,sklearn调包)
目录1. 决策树原理1.1. 特性1.2. 思路1.3. 概念决策树概念信息论2. 公式推导2.1. 构造决策树2.1.1. ID3理论示例缺点2.1.2. C4.5理论示例缺点2.1.3. CART示例对比分析2.2. 剪枝3. 实例3.1. 数据集3.2. ID33.3. C4.53.4. CART3.5. sklearn实现4. 几个注意点(面试问题)5. 运行&am…...

一文搞懂CAS实现原理——怀玉
点个关注,必回关 文章目录CAS原理剖析1、参数解密CAS底层指令CAS(Compare and swap)是一种用于在多线程环境下实现同步功能的机制CAS原理剖析 CAS 被认为是一种乐观锁,有乐观锁,相对应的是悲观锁。 在上述示例中&…...
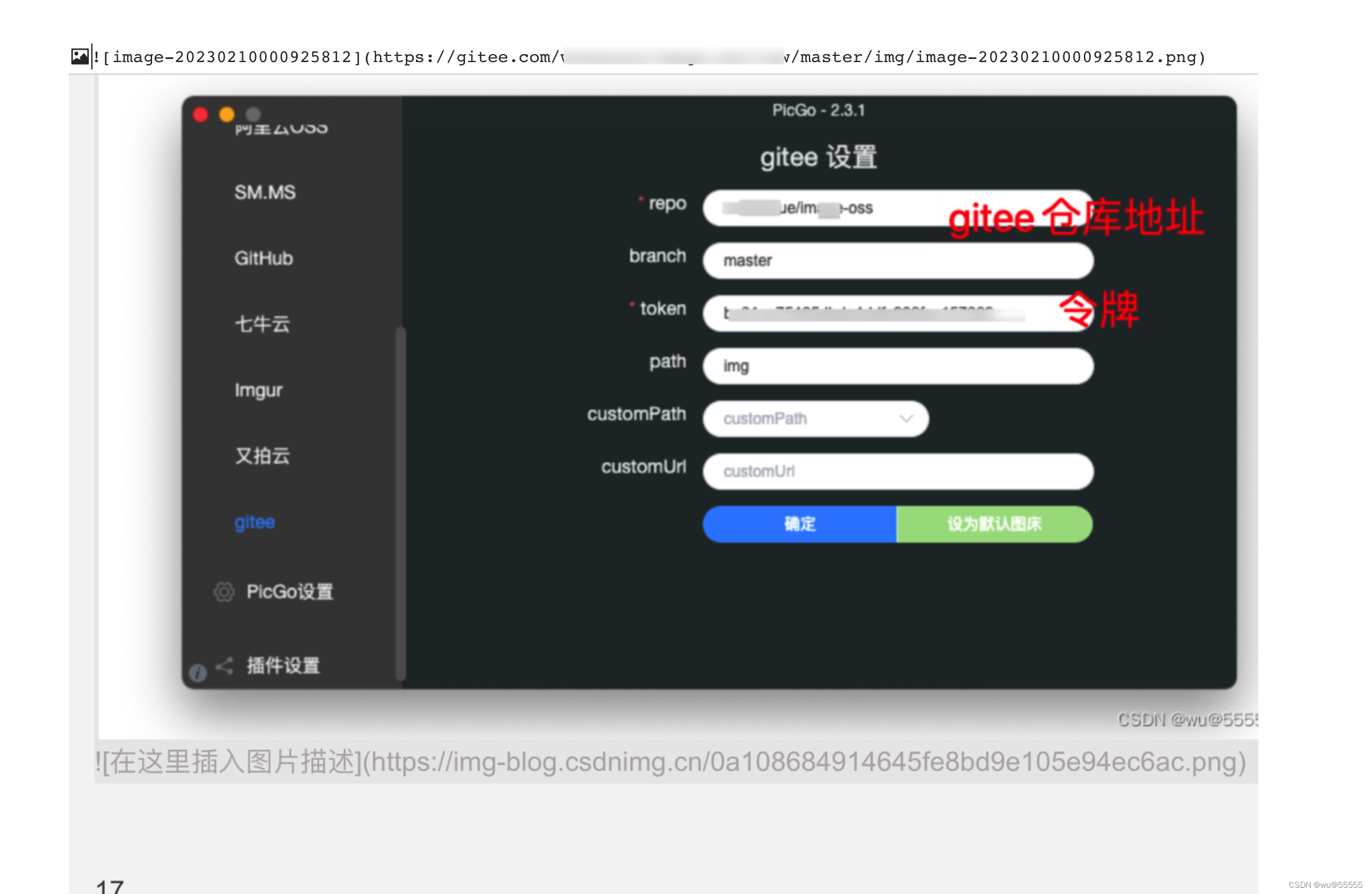
typora每次复制文档都要附带图片文件夹?学会配置gitee图床
0. 引言 作为开发人员,我们习惯使用md格式来编写文档,特别是typora编辑器更是日常使用的软件。但作为轻量化的文档编辑器,我们在默认插入图片时,一般typora会将图片保存到本地或者引用一个本地图片的路径 当文档还在我们本地打开…...
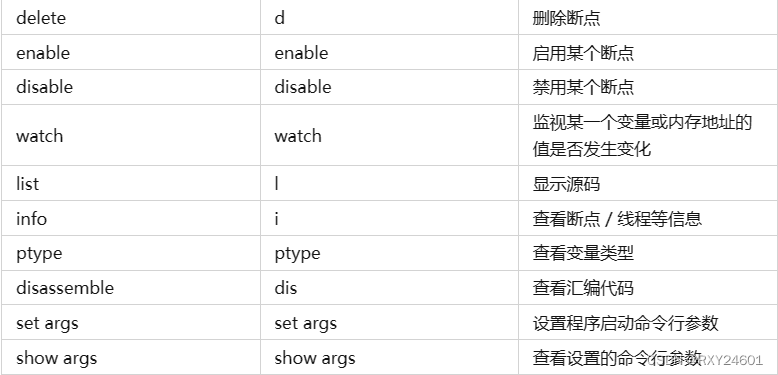
Linux--gdb
gdb用于实现在linux下通过gdb进行调试。由于gcc、g生成的文件是release文件,而不是用于调试的debug文件,所以需要使用gcc -g命令,生成debug文件 调试器:核心工作,主要是为了定位问题 所有查看内容的指令,不…...
(std::multimap)(二))
c++11 标准模板(STL)(std::multimap)(二)
定义于头文件 <map> template< class Key, class T, class Compare std::less<Key>, class Allocator std::allocator<std::pair<const Key, T> > > class multimap;(1)namespace pmr { template <class Key, class T…...

【数据结构】二叉排序树——平衡二叉树的调整
文章目录前置概念一、构造平衡二叉树的基本思想二、一个示例三、平衡二叉树的调整细节(1)LL型(顺时针 )举例(2)RR型(逆时针)(3)LR型(先逆时针再顺…...
)
03- pandas 数据库可视化 (数据库)
pandas库的亮点: 一个快速、高效的DataFrame对象,用于数据操作和综合索引;用于在内存数据结构和不同格式之间读写数据的工具:CSV和文本文件、Microsoft Excel、SQL数据库和快速HDF 5格式;智能数据对齐和丢失数据的综合处理&#…...

第三方电容笔怎么样?开学适合买的电容笔
随着科学技术的进步,很多新型的电子产品和数码设备都出现了。比如手机,IPAD,蓝牙耳机,电容笔等等。实际上,如果你想要更好的使用ipad,那么你就需要一支电容笔。比如ipad,我们用ipad来做笔记&…...

Java学习-IO流-字节输出流
Java学习-IO流-IO流的体系和字节输出流基本用法 //IO流 → 字节流 → 字节输入流:InputStream // ↘ ↘ 字节输出流:OutputStream // ↘ 字符流 → 字符输入流:Reader // ↘ 字符输出流:WriterFileInputStream…...

linux性能分析 性能之巅学习笔记和内容摘录
本文只是在阅读《性能之巅》的过程中,对一些觉得有用的地方进行的总结和摘录,并附加一些方便理解的材料,完整内容还请阅读Gregg的大作 概念和方法 性能分析领域一词的全栈代表了整个操作系统的软硬件在内的所有事物 软件生命周期和性能规划…...
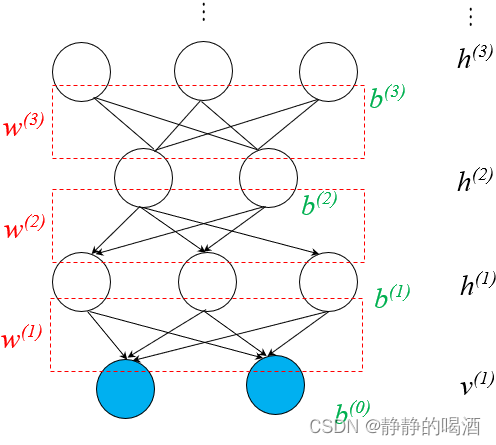
机器学习笔记之生成模型综述(三)生成模型的表示、推断、学习任务
机器学习笔记之生成模型综述——表示、推断、学习任务引言生成模型的表示任务从形状的角度观察生成模型的表示任务从概率分布的角度观察生成模型的表示任务生成模型的推断任务生成模型的学习任务引言 上一节介绍了从监督学习、无监督学习任务的角度介绍了经典模型。本节将从表…...
第八章 Flink集成Iceberg的DataStreamAPI、TableSQLAPI详解
1、概述 目前Flink支持使用DataStream API 和SQL API方式实时读取和写入Iceberg表,建议使用SQL API方式实时读取和写入Iceberg表。 Iceberg支持的Flink版本为1.11.x版本以上,以下为版本匹配关系: Flink版本Iceberg版本备注Flink1.11.XI…...

PyTorch学习笔记:nn.Sigmoid——Sigmoid激活函数
PyTorch学习笔记:nn.Sigmoid——Sigmoid激活函数 torch.nn.Sigmoid()功能:逐元素应用Sigmoid函数对数据进行激活,将元素归一化到区间(0,1)内 函数方程: Sigmoid(x)σ(x)11e−xSigmoid(x)\sigma(x)\frac1{1e^{-x}} Sigmoid(x)σ(…...
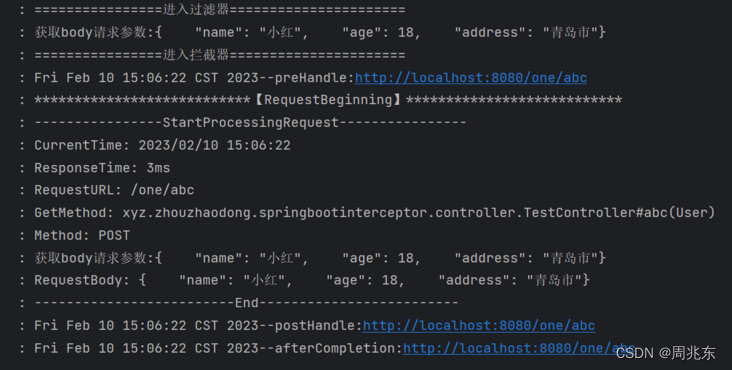
个人学习系列 - 解决拦截器操作请求参数后台无法获取
由于项目需要使用拦截器对请求参数进行操作,可是请求流只能操作一次,导致后面方法不能再获取流了。 新建SpringBoot项目 1. 新建拦截器WebConfig.java /*** date: 2023/2/6 11:21* author: zhouzhaodong* description:*/ Configuration public class W…...
【编程基础之Python】2、安装Python环境
【编程基础之Python】2、安装Python环境安装Python环境在Windows上安装Python验证Python运行环境在Linux上安装Python验证Python运行环境总结安装Python环境 所谓“工欲善其事,必先利其器”。在学习Python之前需要先搭建Python的运行环境。由于Python是跨平台的&am…...
Java开发 - 问君能有几多愁,Spring Boot瞅一瞅。
前言 首先在这里恭祝大家新年快乐,兔年大吉。本来是想在年前发布这篇博文的,奈何过年期间走街串巷,实在无心学术,所以不得不放在近日写下这篇Spring Boot的博文。在还没开始写之前,我已经预见到,这恐怕将是…...
Office Server Document Converter Lib SDK Crack
关于 Office Server 文档转换器 (OSDC) 无需 Microsoft Office 或 Adobe 软件即可快速准确地转换文档。antennahouse.com Office Server 文档转换器 (OSDC) 会将您在 Microsoft Office(Word、Excel、PowerPoint)中创建的重要文档转换为高质量的 PDF …...

Cubox是什么应用?如何将Cubox同步至Notion、语雀、在线文档中
Cubox是什么应用? Cubox 是一款跨平台的网络收藏工具,通过浏览器扩展、客户端、手机应用、微信转发等方式,将网页、文字、图片、语音、视频、文件等内容保存起来,再经过自动整理、标签、分类之后,就可以随时阅读、搜索…...
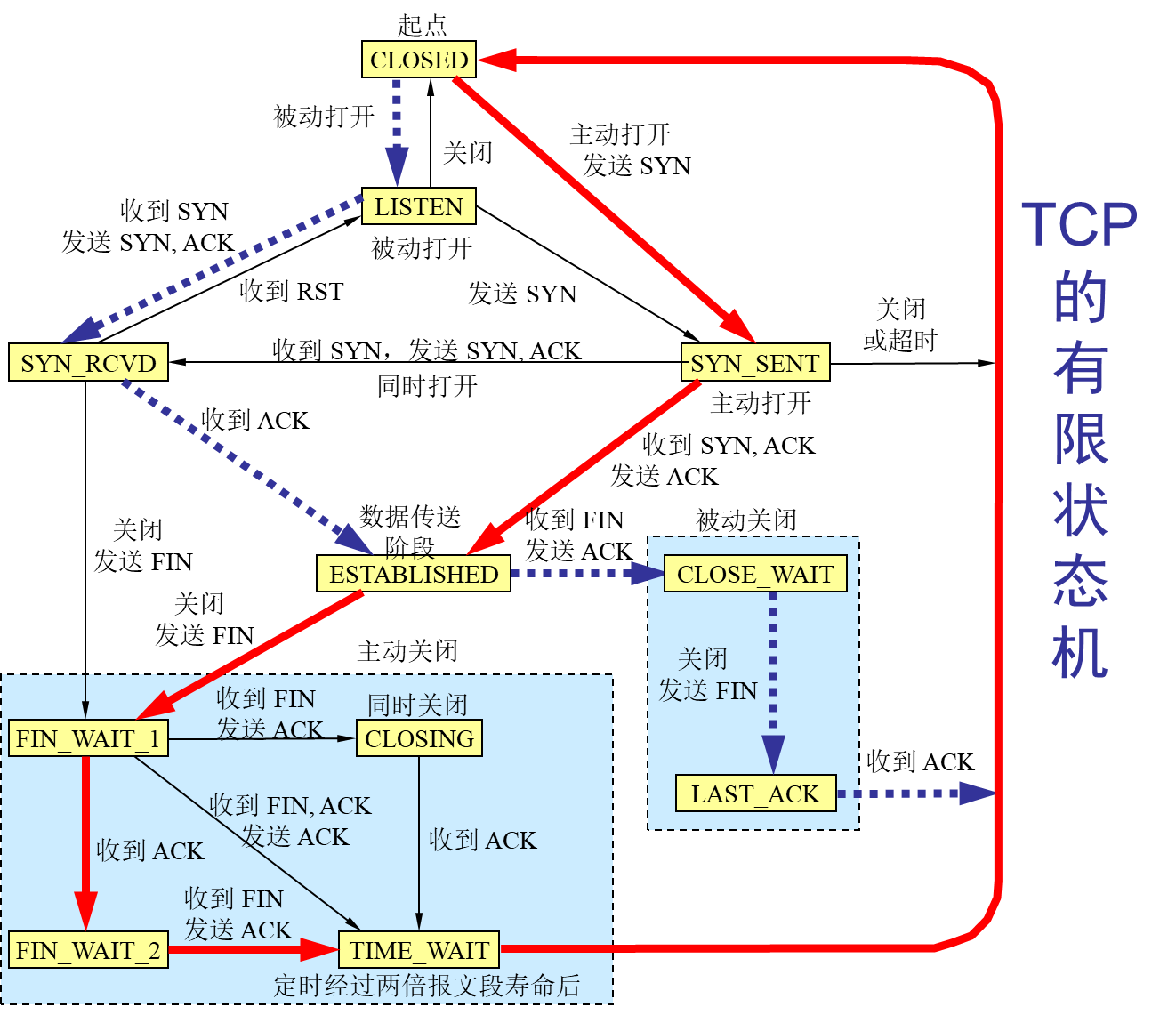
计算机网络-传输层
文章目录前言概述用户数据报协议 UDP(User Datagram Protocol)传输控制协议 TCP(Transmission Control Protocol)TCP 的流量控制拥塞控制方法TCP 的运输连接管理TCP 的有限状态机总结前言 本博客仅做学习笔记,如有侵权,联系后即刻更改 科普:…...

HTML-CSS-js教程
HTML 双标签<html> </html> 单标签<img> html5的DOCTYPE声明 <!DOCTYPE html>html的基本骨架 <!DOCTYPE html> <html> </html>head标签 用于定义文档的头部。文档的头部包含了各种属性和信息,包括文档的标题&#…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...
