自然对数底e的一些事
自然对数底e的一些事
走的人多了就成了路
中国清代数学家李善兰(1811—1882)
凡此变数中函彼变数者,则此为彼之函数
自然对数底也是使用习惯
🍉 李善兰把function翻译为函数,函就是包含,含有变量,自此沿用至今,同时函数又以f开头,所以f g h 三个字母又常用于函数名,而 a b c d 常代表任意常数。而e因为欧拉指代自然对数的底,也就成了今天这个样子。

莱布尼茨(Leibniz)研究此领域时使用字母b

欧拉研究此领域用了字母e,并非欧拉 (Euler. leonhard) 首字母。自此一个伟大的极限就诞生了。
e = lim n → ∞ ( 1 + 1 n ) n \LARGE \begin{aligned} e=\lim\limits_{n\rightarrow \infty}(1+\dfrac{1}{n})^{n} \end{aligned} e=n→∞lim(1+n1)n
如果发现一处通用的模块或者功能,我们就为它起个名字,这就是伟大发现或者发明。
高斯
当一幢建筑物完成时,应该把脚手架拆除干净
有时候就因为这个习惯,感觉就像是天才的傀儡,他们为啥有这样的天才想法,书本里也从来不说,甚至连过程都没有。
如下是实数也成立的证明
应用拉格朗日的夹逼准则
设 n ⩽ x < n + 1 n\leqslant x \lt {n+1} n⩽x<n+1 那么
( 1 + 1 x ) n ⩽ ( 1 + 1 x ) x < ( 1 + 1 x ) n + 1 (步骤A) \large (1+\dfrac{1}{x})^n \leqslant (1+\dfrac{1}{x})^x \lt (1+\dfrac{1}{x})^{n+1}\tag{步骤A} (1+x1)n⩽(1+x1)x<(1+x1)n+1(步骤A)
上式左侧缩小就可以去除等号,右侧放大也依然成立
( 1 + 1 x ) n ⇒ 用 n + 1 替换 x ( 1 + 1 n + 1 ) n ( 1 + 1 x ) n + 1 ⇒ 用 n 替换 x ( 1 + 1 n ) n + 1 \LARGE \begin{aligned} &\boxed{(1+\dfrac{1}{x})^n }\xRightarrow{用n+1替换x}\boxed{(1+\dfrac{1}{n+1})^n } \\ &\boxed{(1+\dfrac{1}{x})^{n+1} }\xRightarrow{用n替换x}\boxed{(1+\dfrac{1}{n})^{n+1} } \end{aligned} (1+x1)n用n+1替换x(1+n+11)n(1+x1)n+1用n替换x(1+n1)n+1
那么步骤A变成了
( 1 + 1 n + 1 ) n < ( 1 + 1 x ) x < ( 1 + 1 n ) n + 1 (步骤B) \large (1+\dfrac{1}{n+1})^n \lt (1+\dfrac{1}{x})^x \lt (1+\dfrac{1}{n})^{n+1}\tag{步骤B} (1+n+11)n<(1+x1)x<(1+n1)n+1(步骤B)
左右两侧如果都是e,通过拉格朗日夹逼准则就证明了正实数也是e
lim n → ∞ ( 1 + 1 n + 1 ) n = lim n → ∞ ( 1 + 1 n + 1 ) n + 1 1 + 1 n + 1 = e lim n → ∞ ( 1 + 1 n ) n + 1 = lim n → ∞ ( 1 + 1 n ) n ( 1 + 1 n ) = e \LARGE \begin{aligned} &\lim\limits_{n\rightarrow \infty}(1+\dfrac{1}{n+1})^n &&= \lim\limits_{n\rightarrow \infty}\dfrac{(1+\dfrac{1}{n+1})^{n+1}}{1+\dfrac{1}{n+1}}&&&=e\\ &\lim\limits_{n\rightarrow \infty}(1+\dfrac{1}{n})^{n+1} &&= \lim\limits_{n\rightarrow \infty}(1+\dfrac{1}{n})^{n} (1+\dfrac{1}{n})&&&=e \end{aligned} n→∞lim(1+n+11)nn→∞lim(1+n1)n+1=n→∞lim1+n+11(1+n+11)n+1=n→∞lim(1+n1)n(1+n1)=e=e
x趋向于正无穷得证
e = lim x → + ∞ ( 1 + 1 x ) x \LARGE \begin{aligned} \boxed{e=\lim\limits_{x\rightarrow +\infty}(1+\dfrac{1}{x})^{x}} \end{aligned} e=x→+∞lim(1+x1)x
设 x = − ( t + 1 ) , 那么 x → − ∞ , 则 t → ∞ x=-(t+1),那么x\rightarrow -\infty,则\, t\rightarrow\infty x=−(t+1),那么x→−∞,则t→∞
lim x → − ∞ ( 1 + 1 x ) x = lim t → ∞ ( 1 − 1 t + 1 ) − ( t + 1 ) = lim t → ∞ ( t t + 1 ) − ( t + 1 ) = lim t → ∞ ( t + 1 t ) ( t + 1 ) = lim t → ∞ ( 1 + 1 t ) ( t + 1 ) = lim t → ∞ ( 1 + 1 t ) t ( 1 + 1 t ) = e \LARGE \begin{aligned} \\ \lim\limits_{x\rightarrow -\infty}(1+\dfrac{1}{x})^x &= \lim\limits_{t\rightarrow \infty}(1-\dfrac{1}{t+1})^{-(t+1)} = \lim\limits_{t\rightarrow \infty}(\dfrac{t}{t+1})^{-(t+1)}\\ &= \lim\limits_{t\rightarrow \infty}(\dfrac{t+1}{t})^{(t+1)}=\lim\limits_{t\rightarrow \infty}(1+\dfrac{1}{t})^{(t+1)}\\ &=\lim\limits_{t\rightarrow \infty}(1+\dfrac{1}{t})^t(1+\dfrac{1}{t})\\ &=e \end{aligned} x→−∞lim(1+x1)x=t→∞lim(1−t+11)−(t+1)=t→∞lim(t+1t)−(t+1)=t→∞lim(tt+1)(t+1)=t→∞lim(1+t1)(t+1)=t→∞lim(1+t1)t(1+t1)=e
至此实数公式得证
e = lim x → ∞ ( 1 + 1 x ) x \LARGE \begin{aligned} \fcolorbox{#ffae42}{#2E8B57}{\textcolor{White}{$e=\lim\limits_{x\rightarrow \infty}(1+\dfrac{1}{x})^{x}$}} \end{aligned} e=x→∞lim(1+x1)x
为什么要创造 l n ln ln函数?
l o g a x log_ax logax 如果进行抽象就是算子[自变量],算子就是 l o g a [ ] log_a[\quad] loga[] 那么a代表任意常数,如果用一个确定的 e e e似乎曲解了原意, l o g e [ ] e log_e[\quad] \quad e loge[]e 并不是代表任意常数。
l o g e [ ] log_e[\quad] loge[] 也不够简洁, l n ln ln 就制造出来了,通用功能给起个名字就是创造。
logarithm 与 nature 各取首字母就成了新的算子 l n [ ] ln[\quad] ln[]
相关文章:

自然对数底e的一些事
自然对数底e的一些事 走的人多了就成了路 中国清代数学家李善兰(1811—1882) 凡此变数中函彼变数者,则此为彼之函数 自然对数底也是使用习惯 🍉 李善兰把function翻译为函数,函就是包含,含有变量ÿ…...

React Hooks 全解:零基础入门
Hooks 的由来 你还在为该使用无状态组件(Function)还是有状态组件(Class)而烦恼吗? ——拥有了hooks,你再也不需要写Class了,你的所有组件都将是Function。 你还在为搞不清使用哪个生命周期钩…...

webrtc在js里的实现
WebRTC(Web Real-Time Communication)是一项开放的浏览器技术,它允许浏览器之间建立点对点(peer-to-peer)连接,实现音频、视频、文件的传输和通信。它的实现一般需要使用JavaScript语言。 在JavaScript中&…...

熊猫:完整的初学者指南
pandas:完整的初学者指南 一、说明 在你的Python开发人员或数据科学之旅中,你可能已经多次遇到“熊猫”这个词,但仍然需要弄清楚它的作用。以及数据和熊猫之间的关系。所以让我向你解释一下。 根据最新估计,每天创建 328.77 亿 TB…...

【Go】Go语言并发编程:原理、实践与优化
在当今的计算机世界,多核处理器和并发编程已经成为提高程序执行效率的关键。Go语言作为一门极富创新性的编程语言,凭借其强大的并发能力,在这方面表现出色。本文将深入探讨Go语言并发编程的原理,通过实际代码示例展示其应用&#…...
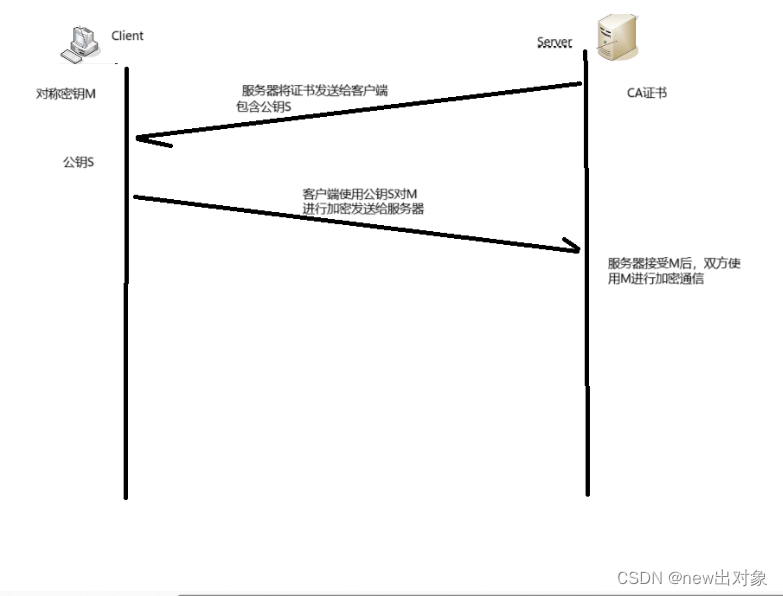
HTTPS协议加密原理
目录 一、什么是HTTPS 二、什么是加密/解密 三、为什么要加密 四、常见的加密方式 1.对称加密 2. 非对称加密 五、HTTPS加密方式探讨 1.只使用对称加密 2.只使用非对称加密 3.非对称加密对称加密 4.非对称加密对称加密CA认证 六、总结 一、什么是HTTPS HTTP 协议&a…...
 测试点全过)
L1-034 点赞(Python实现) 测试点全过
题目 微博上有个“点赞”功能,你可以为你喜欢的博文点个赞表示支持。每篇博文都有一些刻画其特性的标签,而你点赞的博文的类型,也间接刻画了你的特性。本题就要求你写个程序,通过统计一个人点赞的纪录,分析这个人的特…...

MySQL 存储过程 循环处理数据 while repeat
最近搞数据,需要搞搞mysql 的存储过程,很多忘记了,就查查,然后总结下。。 文章目录 介绍循环repeat方式循环while方式外传 介绍 MySQL存储过程中使用循环处理数据 存储过程就像一份写好的由多条SQL组合的代码,这份SQ…...

基于配置类方式管理 Bean
目录 一、完全注解开发理解 二、配置类和扫描注解 三、Bean定义组件 四、Bean注解细节 五、import 扩展 一、完全注解开发理解 Spring 完全注解配置(Fully Annotation-based Configuration)是指通过 Java配置类 代码来配置 Spring 应用程序&#…...
最新CMS指纹识别技术
指纹识别 1.CMS简介 CMS(Content Management System,内容管理系统),又称整站系统或文章系统,用于网站内容管理。用户只需下载对应的CMS软件包,部署、搭建后就可以直接使用CMS。各CMS具有独特的…...

快速入门学习记录:常用代码、特定函数、复杂概念和特定功能说明
😀前言 本篇博文是关于Java入门学习的一些常用记录,希望你能够喜欢 🏠个人主页:晨犀主页 🧑个人简介:大家好,我是晨犀,希望我的文章可以帮助到大家,您的满意是我的动力&a…...
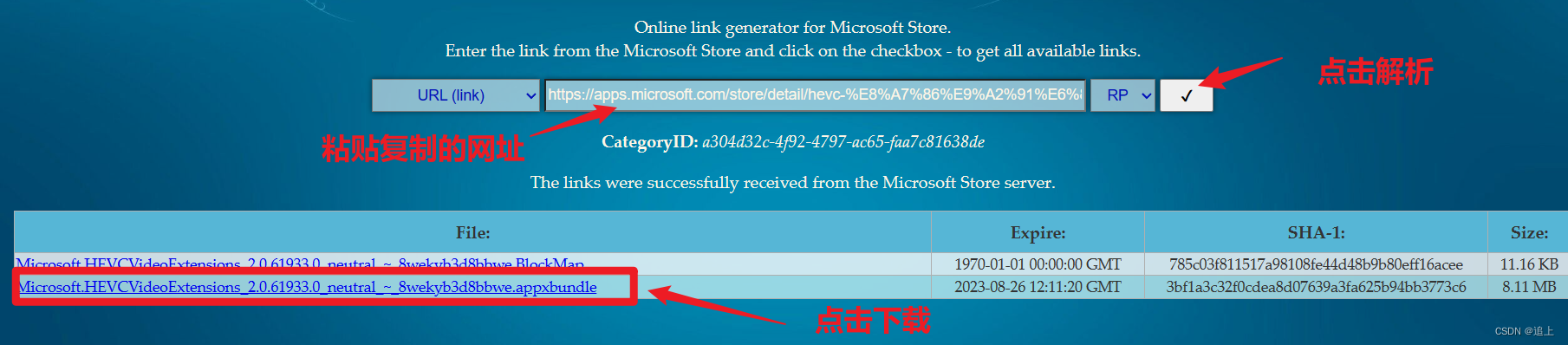
【win视频播放器】HEVC视频扩展
问题描述: 播放此视频需要新的编解码器 编解码器允许应用读取并播放不同文件。可以从Microsoft Store下载该编解码器 ¥7.00 现在获取 稍后再说 解决方法: 方法一:(该方法我正常使用) 链接:ht…...
React+Typescript 父子组件事件传值
好 之前我们将 state 状态管理简单过了一下 那么 本文 我们来研究一下事假处理 点击事件上文中我们已经用过了 这里 我们就不去讲了 主要来说说 父子之间的事件 我们直接来编写一个小dom 我们父组件 编写代码如下 import Hello from "./components/hello";functio…...

python人工智能和机器学习
人工智能和机器学习是当今科技领域最热门和前沿的话题之一。随着数据的爆炸式增长和计算能力的提升,人工智能和机器学习在各个领域都有广泛的应用。Python作为一种易学易用且功能强大的编程语言,已经成为人工智能和机器学习的首选工具之一。本文将介绍Py…...

[PyTorch][chapter 51][Auto-Encoder -1]
目录: 简介 损失函数 自动编码器的类型 一 AutoEncoder 简介: 自动编码器是一种神经网络,用于无监督学习任务.(没有标签或标记数据), 例如降维,特征提取和数据压缩. 主要任务: 1: 输入数据 …...

Uniapp或者微信小程序如何动态的计算Scrollview的高度
当一个小程序页面,顶部有搜索栏,或者分类查询时,我们想要保证它们能固定到顶部,就需要使用到Scrollview,那么如何确定Scrollview就是一个问题,这时我们可以使用以下代码来实现 setScrollHeight(view #scr…...

Abase数据库管理系统
Abase数据库管理系统的架构介绍如下: 1. 概述 Abase是一个开源的分布式数据库中间件,实现MySQL数据库的自动扩缩容、故障转移和查询路由。 2. 功能架构 - 读写分离:拆分为主从两套服务 - 自动扩缩容:根据负载水平完成扩容 - 负载均衡:基于查询解析的路由 - 故障转移:快速切换…...
系统架构设计高级技能 · 大数据架构设计理论与实践
系列文章目录 系统架构设计高级技能 软件架构概念、架构风格、ABSD、架构复用、DSSA(一)【系统架构设计师】 系统架构设计高级技能 系统质量属性与架构评估(二)【系统架构设计师】 系统架构设计高级技能 软件可靠性分析与设计…...

ubuntu上使用osg3.2+osgearth2.9
一、介绍 在ubuntu上使用osgearth加载三维数字地球,首先要有osg和osgearth的库,这些可以直接使用apt-get下载安装,但是版本有些老,如果需要新版本的就需要自己编译。 #查看现有版本 sudo apt-cache madison openscenegraph #安装…...

C语言巧妙打印64位整数
使用C语言打印64位整数时,如果用的是32位编译器,那么打印如下, int64_t data 0x1234567890123456; printf("0x%llx\n", data);如果是64位编译器,那么打印代码如下, int64_t data 0x1234567890123456; pr…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

