matlab使用教程(21)—求函数最值
1. 求函数最优值
1.1求一元函数的最小值
x = -1:.01:2;
y = humps(x);
plot(x,y)
xlabel('x')
ylabel('humps(x)')
grid on
若要计算 humps 函数在 (0.3,1) 范围内的最小值,请使用
x = fminbnd(@humps,0.3,1)options = optimset('Display','iter');
x = fminbnd(@humps,0.3,1,options)1.2 求多元函数的最小值
function b = three_var(v)
x = v(1);
y = v(2);
z = v(3);
b = x.^2 + 2.5*sin(y) - z^2*x^2*y^2;v = [-0.6,-1.2,0.135];
a = fminsearch(@three_var,v)1.3 求函数最大值

[x fval] = fminbnd(@(x)-tan(cos(x)),3,8)1.4 fminsearch 算法

2.非线性函数的数据拟合
2.1 创建样本数据
rng default % for reproducibility
tdata = 0:0.1:10;
ydata = 40*exp(-0.5*tdata) + randn(size(tdata));2.2 编写目标函数
type ssevalfun = @(x)sseval(x,tdata,ydata);2.3 求最优拟合参数
x0 = rand(2,1);
bestx = fminsearch(fun,x0)2.4 检查拟合质量
A = bestx(1);
lambda = bestx(2);
yfit = A*exp(-lambda*tdata);
plot(tdata,ydata,'*');
hold on
plot(tdata,yfit,'r');
xlabel('tdata')
ylabel('Response Data and Curve')
title('Data and Best Fitting Exponential Curve')
legend('Data','Fitted Curve')
hold off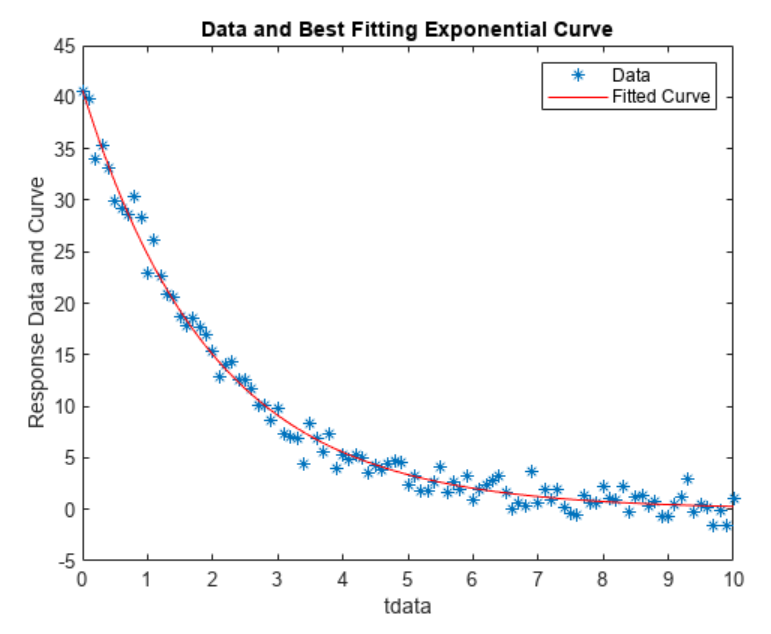
相关文章:

matlab使用教程(21)—求函数最值
1. 求函数最优值 1.1求一元函数的最小值 如果给定了一个一元数学函数,可以使用 fminbnd 函数求该函数在给定区间中的局部最小值。例如,请考虑 MATLAB 提供的 humps.m 函数。下图显示了 humps 的图。 x -1:.01:2; y humps(x); plot(x,y) xlabel(x)…...

Redis中 为什么Lua脚本可以保证原子性?
Redis中 为什么Lua脚本可以保证原子性?...

tda4 videnc-test-app: CONTINUOUS and STEPWISE FRAMEINTERVALS not supported
/* videnc-test-app */ https://git.ti.com/cgit/jacinto7_multimedia/ git clone https://git.ti.com/git/jacinto7_multimedia/videnc-test-app.git // 编译 ./autogen.sh ./configure --enable-maintainer-mode --buildi386-linux --hostaarch64-none-linux CC/home/share…...

[已解决] libGL error: MESA-LOADER: failed to open swrast
在新的服务器中配置好虚拟环境后,利用已有的预训练模型test后,可视化时遇到: libGL error: MESA-LOADER: failed to open swrast: /usr/lib/dri/swrast_dri.so: cannot open shared object file: No such file or directory (search paths /u…...
JVM及垃圾回收机制
文章目录 1、JVM组成?各部分作用?1.1 类加载器(Class Loaders)1.2 运行时数据区(Runtime Data Area)1.3 执行引擎(Execution Engine)1.4 本地方法接口(Native Interface&…...
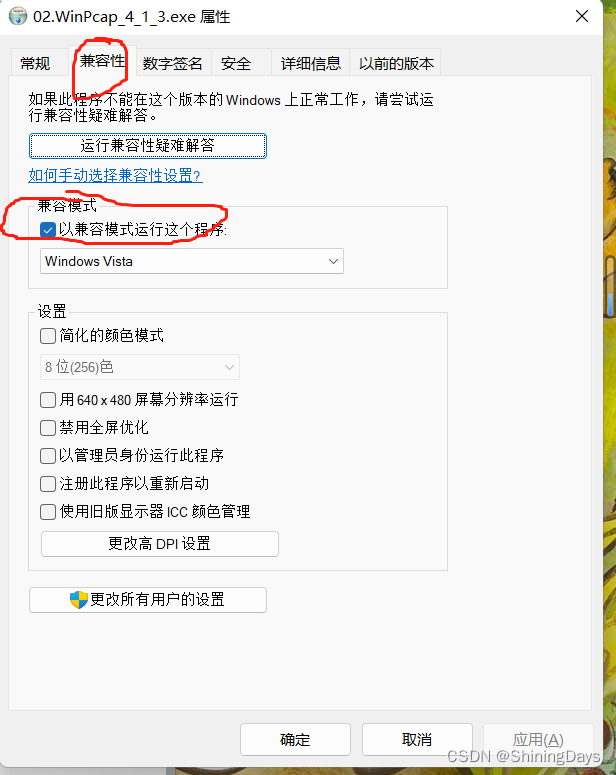
windows11不允许安装winpcap4.1.3
问题:下载安装包后在安装时显示与电脑系统不兼容,不能安装。 原因:winpcap是一个用于Windows操作系统的网络抓包库,有一些安全漏洞,存在被黑客攻击的风险。Windows11为了加强系统安全而禁用了这个库,因此不…...
—优化函数的参数)
matlab使用教程(23)—优化函数的参数
本博客向您介绍如何存储或访问向 MATLAB 复合函数(如 fzero 或 integral)传递的数学函数的额外参数。 MATLAB 复合函数基于某个值范围计算数学表达式。这些函数之所以称为复合函数是因为它们是接受函数句柄(函数的指针)作为输入…...

基于“互联网+ 服务供应链”的汽车道路救援系统对策分析
1。 建立“互联网服务供应链”背景下汽车道路救援系统 基于互联网的汽车道路救援,两级服务供应链结构是由服务提供商、服务 集成商和客户组成。“互联网服务供应链”背景下汽车道路救援系统组成, 它是一种 B2B2C 的形式,与前述传统汽车道路…...
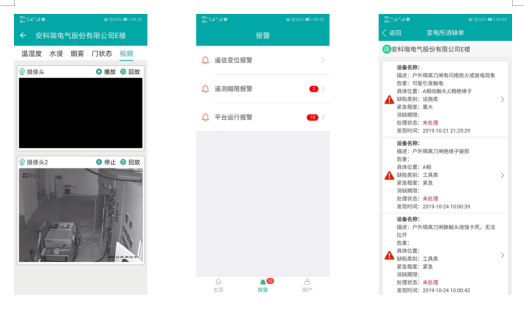
浅谈泛在电力物联网在电力设备状态在线监测中的应用
安科瑞 华楠 摘要:随着信息化水平的不断发展,泛在电力物联网的建设提上日程,这对提升变电站电力设备在线监测水平,推动智能电网发展具有重要的指导意义。对基于物联网的电力设备状态监测系统进行了研究,概括了泛在电力…...

低通滤波器和高通滤波器
应用于图像低通滤波器和高通滤波器的实现 需要用到傅里叶变换 #include <opencv2/opencv.hpp> #include <Eigen> #include <iostream> #include <vector> #include <cmath> #include <complex>#define M_PI 3.14159265358979323846…...

VS中插入Qt插件后配置项目笔记
Project下要创建四个文件夹: bin(输出目录\工作目录) 、include(头文件目录) 、lib(动态库目录) 、src(源码目录) 一、主项目模块配置: 1.配置属性——>常规——>输出目录加入(..\..\bin\) 2.配置属性——>调试——>工作目录加入($(OutDir)) 备注&am…...
Hugo·Stack主题·使用及修改
代码折叠 cp themes/hugo折-themt-saick/exampleSlte/config.yamsclass"codefold"><summary class"codefold__title"><span class"codefold__title-text">" {{ with .Get 0}}{{.}}{{else}}click to expand{{ end }} "&…...
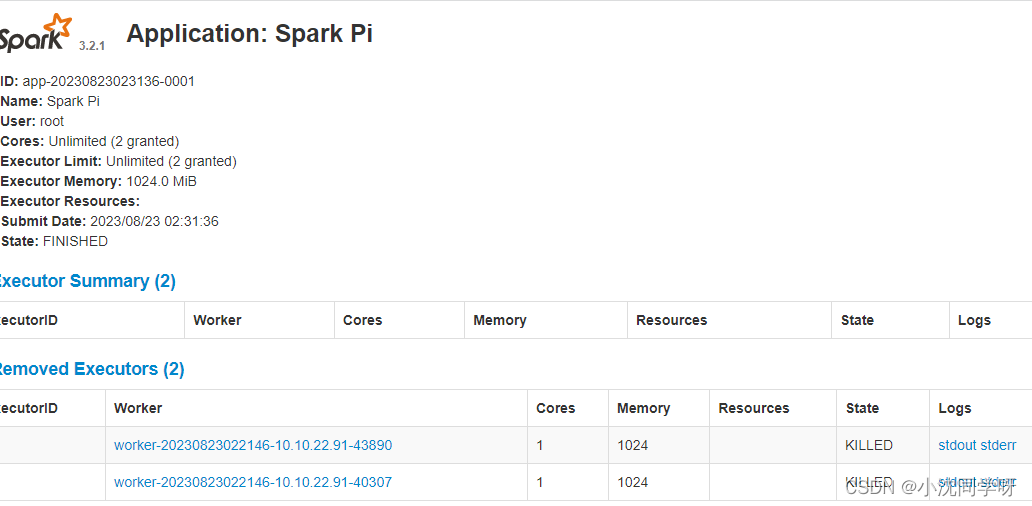
实战:大数据Spark简介与docker-compose搭建独立集群
文章目录 前言技术积累Spark简介Spark核心功能及优势Spark运行架构 Spark独立集群搭建安装docker和docker-composedocker-compose编排docker-compose编排并运行容器 Spark集群官方案例测试写在最后 前言 很多同学都使用过经典的大数据分布式计算框架hadoop,其分布式…...

嵌入性视角下的企业集成创新网络演化过程
从嵌入性角度来看,集成创新网络以社会关系嵌入或结构嵌入的联结方式,实 现创新资源共享。由于规模经济和能力的差异,较高的信息复杂程度往往更强调网 络化和外部组织之间的联合而不是一体化。企业集成创新网络依靠创新网络结点上 企业的合…...

回归预测 | MATLAB实现FA-ELM萤火虫算法优化极限学习机多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现FA-ELM萤火虫算法优化极限学习机多输入单输出回归预测(多指标,多图) 目录 回归预测 | MATLAB实现FA-ELM萤火虫算法优化极限学习机多输入单输出回归预测(多指标,多图)效果一览基本介绍…...
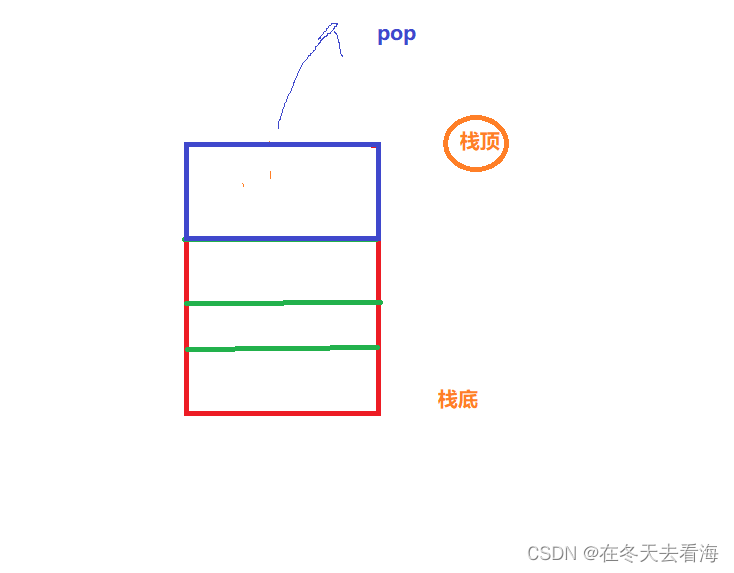
数据结构数组栈的实现
Hello,今天我们来实现一下数组栈,学完这个我们又更进一步了。 一、栈 栈的概念 栈是一种特殊的线性表,它只允许在固定的一端进行插入和删除元素的操作。 进行数据的插入和删除只在栈顶实现,另一端就是栈底。 栈的元素是后进先出。…...

成集云 | 抖店连接器客户静默下单催付数据同步钉钉 | 解决方案
源系统成集云目标系统 方案介绍 随着各品牌全渠道铺货,主播在平台上直播时客户下了订单后不能及时付款,第一时间客户收不到提醒,不仅造成了客户付款率下降,更大量消耗了企业的人力成本和经济。而成集云与钉钉深度合作࿰…...

【算法专题突破】双指针 - 复写零(2)
目录 1. 题目解析 2. 算法原理 3. 代码编写 写在最后: 1. 题目解析 题目链接:1089. 复写零 - 力扣(Leetcode) 我先来读题, 题目的意思非常的简单,其实就是, 遇到 0 就复制一个写进数组&a…...
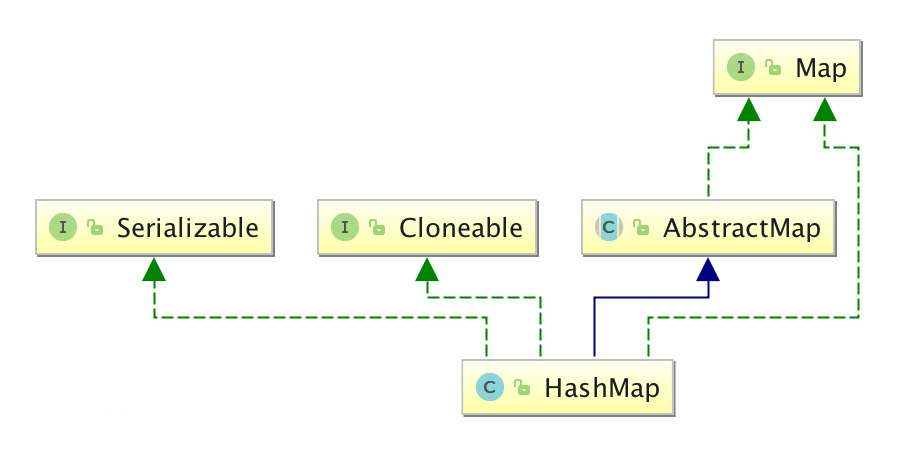
【Java从0到1学习】11 Java集合框架
1. Collection 1.1 Java类中集合的关系图 1.2 集合类概述 在程序中可以通过数组来保存多个对象,但在某些情况下开发人员无法预先确定需要保存对象的个数,此时数组将不再适用,因为数组的长度不可变。例如,要保存一个学校的学生信…...
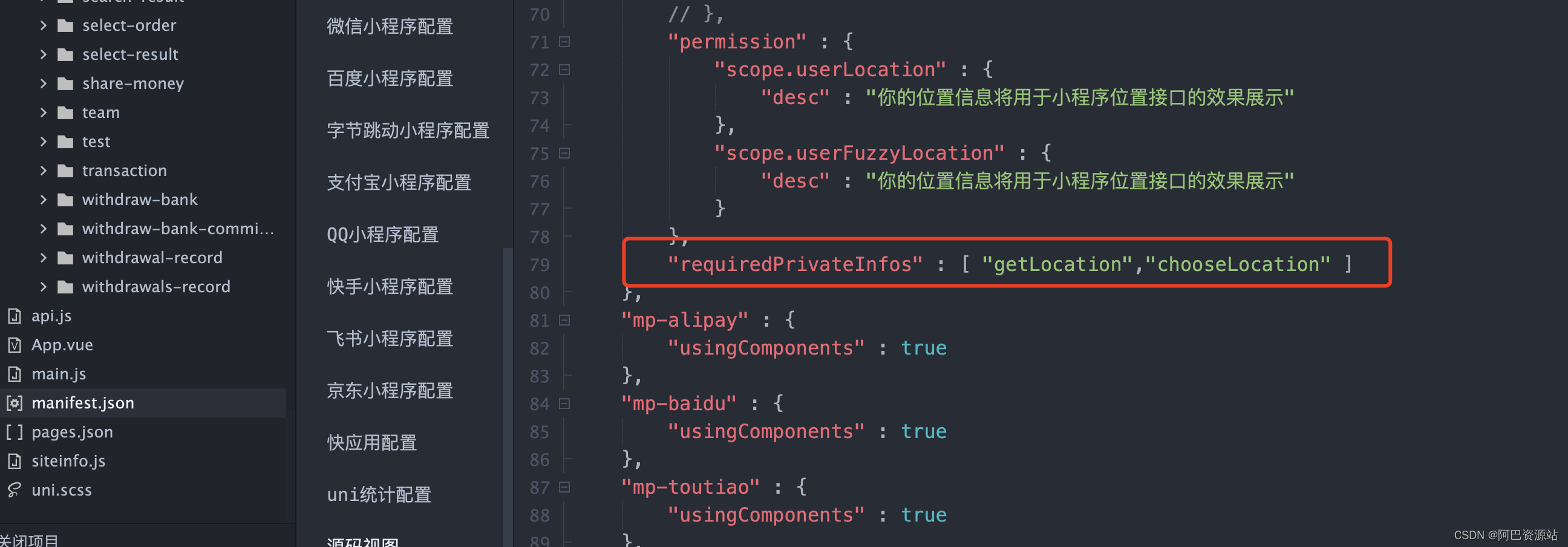
uniapp使用uni.chooseLocation()打开地图选择位置
使用uni.chooseLocation()打开地址选择位置: 在Uniapp源码视图进行设置 添加这个属性:"requiredPrivateInfos":["chooseLocation"] </template><view class"location_box"><view class"locatio…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...
