(动态规划) 剑指 Offer 10- II. 青蛙跳台阶问题 ——【Leetcode每日一题】
❓剑指 Offer 10- II. 青蛙跳台阶问题
难度:简单
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入:n = 2
输出:2
示例 2:
输入:n = 7
输出:21
示例 3:
输入:n = 0
输出:1
提示:
0 <= n <= 100
注意:本题与 70. 爬楼梯 相同。
💡思路:动态规划
当 n = 1 时,只有一种跳法:
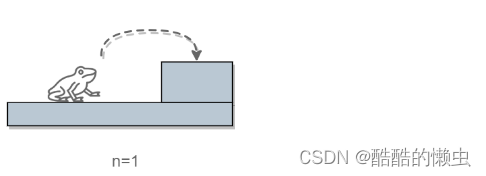
当 n = 2 时,有两种跳法:

跳 n 阶台阶,可以先跳 1 阶台阶,再跳 n-1 阶台阶;或者先跳 2 阶台阶,再跳 n-2 阶台阶。而 n-1 和 n-2 阶台阶的跳法可以看成子问题,该问题的递推公式为:
f ( n ) = { 1 n = 0 1 n = 1 2 n = 2 f ( n − 1 ) + f ( n − 2 ) n > 1 f(n)=\left\{\begin{array}{rcc}1&\quad n=0\\1&\quad n=1\\2&\quad n=2\\f(n-1)+f(n-2)&\quad n>1\end{array}\right. f(n)=⎩ ⎨ ⎧112f(n−1)+f(n−2)n=0n=1n=2n>1
🍁代码:(C++、Java)
C++
class Solution {
public:int numWays(int n) {int ans = 1;int pre1 = 1, pre2 = 1;for(int i = 2; i <= n; i++){ans = (pre1 + pre2) % 1000000007;pre1 = pre2;pre2 = ans;}return ans;}
};
Java
class Solution {public int numWays(int n) {int ans = 1;int pre1 = 1, pre2 = 1;for(int i = 2; i <= n; i++){ans = (pre1 + pre2) % 1000000007;pre1 = pre2;pre2 = ans;}return ans;}
}
🚀 运行结果:
🕔 复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n),循环执行
n次,每次花费常数的时间代价,故渐进时间复杂度为 O ( n ) O(n) O(n)。 - 空间复杂度: O ( 1 ) O(1) O(1),只用了常数个变量作为辅助空间。
题目来源:力扣。
放弃一件事很容易,每天能坚持一件事一定很酷,一起每日一题吧!
关注我LeetCode主页 / CSDN—力扣专栏,每日更新!
注: 如有不足,欢迎指正!
相关文章:

(动态规划) 剑指 Offer 10- II. 青蛙跳台阶问题 ——【Leetcode每日一题】
❓剑指 Offer 10- II. 青蛙跳台阶问题 难度:简单 一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。 答案需要取模 1e97(1000000007),如计算初始结果为:1…...

物联网WIFI 模块AT指令版本七大元凶
前言 目前我们讨论的这个问题,并不是说WIFI方案不具备以应的功能。而是指在同一个AT固件下可能存在的问题。由于各厂商AT指令的开发深度不同,导致各厂商之间的AT指令差异很大。我总结了一些问题,可能是导致目前AT指令不好用元凶。 底层库问题…...
)
Qt 正则(数据格式校验、替换指定格式数据、获取匹配数据)
头文件引用 #include <QRegExp>初始化QRegExp实列 QRegExp re("^\\d{1,3},\\d{1,3}$");数据格式验证 QRegExp re("^\\d{1,3},\\d{1,3}$"); QString msg "12,33"; if(re.exactMatch()){// 验证通过 }else{//验证不通过 }替换数…...

网络层协议——ip
文章目录 1. 网络层2. IP协议2.1 协议头格式 3. 网段划分3.1 特殊的IP地址3.2 IP地址的数量限制 4. 私有IP地址和公网IP地址 1. 网络层 在应用层解决了如何读取完整报文、序列化反序列化、协议处理问题。在传输层解决了可靠性问题。那么网络层IP的作用是在复杂的网络环境中确定…...
Qt6和Rust结合构建桌面应用
桌面应用程序是原生的、快速的、安全的,并提供Web应用程序无法比拟的体验。 Rust 是一种低级静态类型多范式编程语言,专注于安全性和性能,解决了 C/C 长期以来一直在努力解决的问题,例如内存错误和构建并发程序。 在桌面应用程序开…...
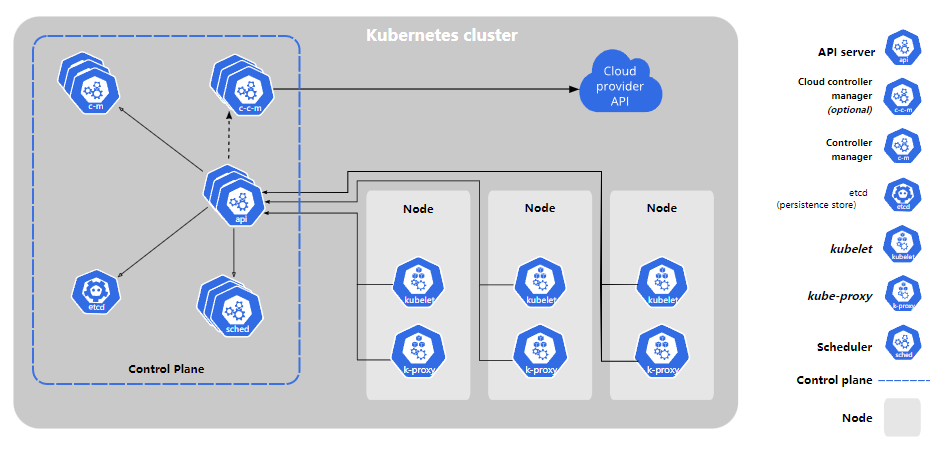
Kubernetes(K8S)简介
Kubernetes (K8S) 是什么 它是一个为 容器化 应用提供集群部署和管理的开源工具,由 Google 开发。Kubernetes 这个名字源于希腊语,意为“舵手”或“飞行员”。k8s 这个缩写是因为 k 和 s 之间有八个字符的关系。 Google 在 2014 年开源了 Kubernetes 项…...

面试中问:React中函数组件和class组件的区别,hooks模拟生命周期
React中函数组件和class组件的区别,hooks模拟生命周期 React中函数组件和class组件的区别hooks模拟生命周期 React中函数组件和class组件的区别 函数组件: 定义:函数组件是使用纯函数定义的组件,它接受 props 作为参数并返回 JSX。简洁性&am…...
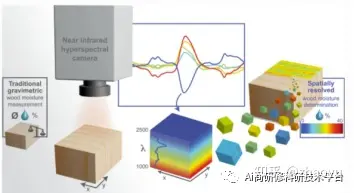
Python高光谱遥感数据处理与高光谱遥感机器学习方法应用
本文提供一套基于Python编程工具的高光谱数据处理方法和应用案例。 本文涵盖高光谱遥感的基础、方法和实践。基础篇以学员为中心,用通俗易懂的语言解释高光谱的基本概念和理论,旨在帮助学员深入理解科学原理。方法篇结合Python编程工具,专注…...

Java实现接收xml格式数据并解析,返回xml格式数据
需求描述:后端接受xml格式数据,解析出相应数据,并返回xml格式数据。 <!--XML解析--><dependency><groupId>com.fasterxml.jackson.dataformat</groupId><artifactId>jackson-dataformat-xml</artifactId>…...

【C++】初步认识模板
🏖️作者:malloc不出对象 ⛺专栏:C的学习之路 👦个人简介:一名双非本科院校大二在读的科班编程菜鸟,努力编程只为赶上各位大佬的步伐🙈🙈 目录 前言一、泛型编程二、函数模板2.1 函…...

Ansible 临时命令搭建安装仓库
创建一个名为/ansible/yum.sh 的 shell 脚本,该脚本将使用 Ansible 临时命令在各个受管节点上安装 yum 存储库. 存储库1: 存储库的名称为 EX294_BASE 描述为 EX294 base software 基础 URL 为 http://content/rhel8.0/x86_64/dvd/BaseOS GPG 签名检查为…...

phpstorm动态调试
首先在phpstudy搭建好网站,在管理拓展开启xdebug拓展 查看php.ini配置已经更改 需要增添修改一下设置 [Xdebug] zend_extensionD:/phpstudy_pro/Extensions/php/php5.6.9nts/ext/php_xdebug.dll xdebug.collect_params1 xdebug.collect_return1 xdebug.auto_trace…...

二叉树的层序遍历及完全二叉树的判断
文章目录 1.二叉树层序遍历 2.完全二叉树的判断 文章内容 1.二叉树层序遍历 二叉树的层序遍历需要一个队列来帮助实现。 我们在队列中存储的是节点的地址,所以我们要对队列结构体的数据域重定义, 以上代码 从逻辑上来讲就是1入队,1出队&am…...
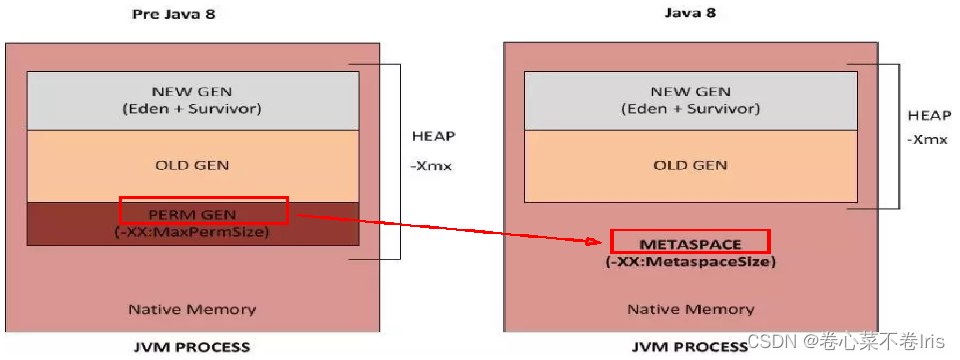
java八股文面试[JVM]——JVM内存结构
参考: JVM学习笔记(一)_卷心菜不卷Iris的博客-CSDN博客 JVM是运行在操作系统之上的,它与硬件没有直接的交互 JVM内存结构: 方法区:存储已被虚拟机加载的类元数据信息(元空间) 堆:存放对象实…...
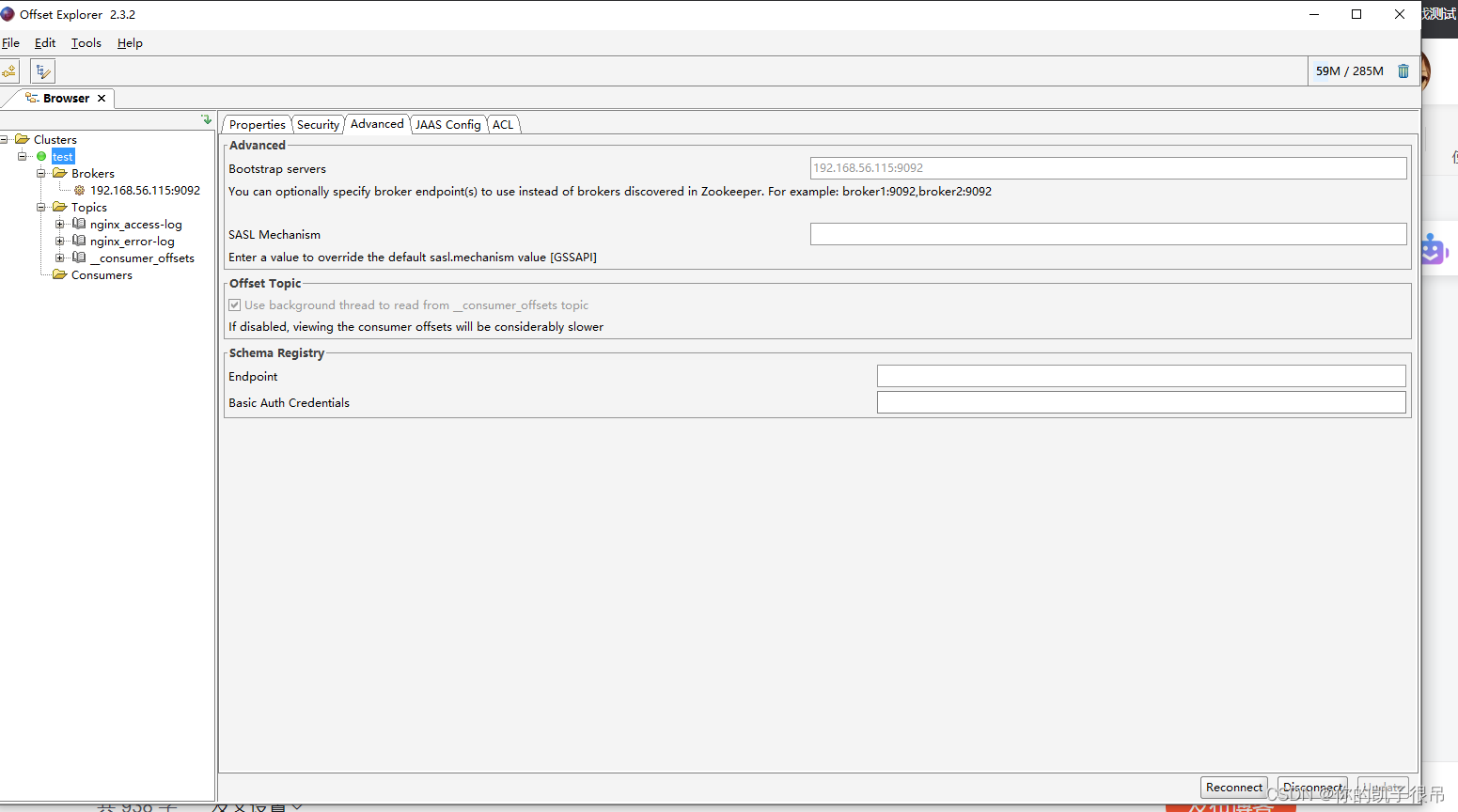
Kafka基本使用
查看Kafka的进程是否在运行 #命令行终端中运行如下命令 ps -ef | grep kafkafind / -iname kafka-server-start.shcd /usr/local/kafka/bin/#启动kafka ./kafka-server-start.sh -daemon /usr/local/kafka/config/server.propertiesKafka默认使用9092端口提供服务…...
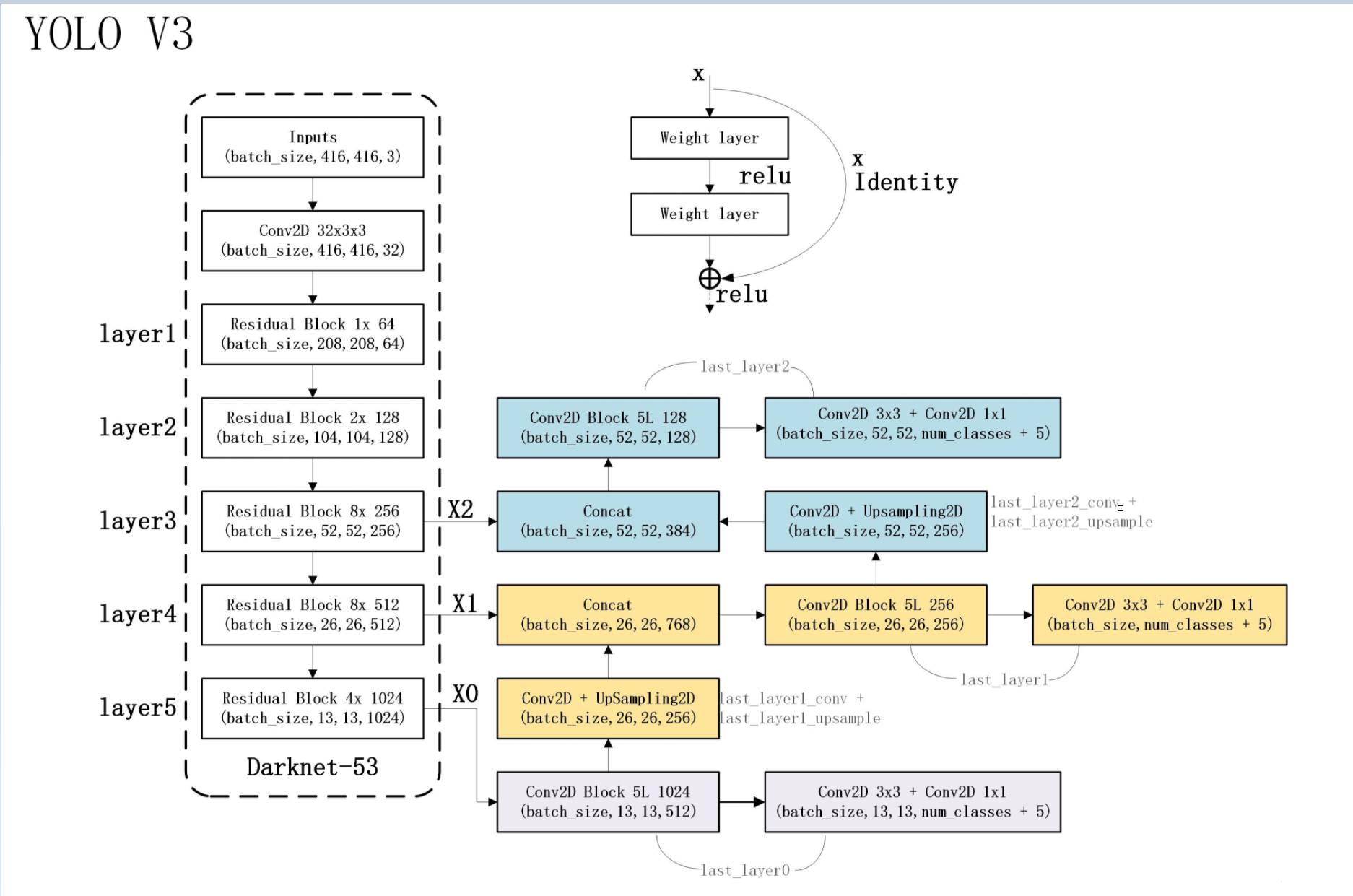
【目标检测】理论篇(2)YOLOv3网络构架及其代码实现
网络构架图: 代码实现: import math from collections import OrderedDictimport torch.nn as nn#---------------------------------------------------------------------# # 残差结构 # 利用一个1x1卷积下降通道数,然后利用一个3x3卷…...

k8s之工作负载、Deployment、DaemonSet、StatefulSet、Job、CronJob及GC
文章目录 1、工作负载1.1、定义1.2、分类 2、Deployment2.1、定义2.2、Deployment创建2.3、Deployment 更新机制2.3.1、比例缩放(Proportional Scaling)2.3.2、HPA(动态扩缩容)2.3.2.1、需要先安装metrics-server2.3.2.2、配置hpa…...
IDEA项目实践——Element UI概述
系列文章目录 IDEA项目实践——JavaWeb简介以及Servlet编程实战 IDEA项目实践——Spring当中的切面AOP IDEA项目实践——Spring框架简介,以及IOC注解 IDEA项目实践——动态SQL、关系映射、注解开发 IDEWA项目实践——mybatis的一些基本原理以及案例 文章目录 …...
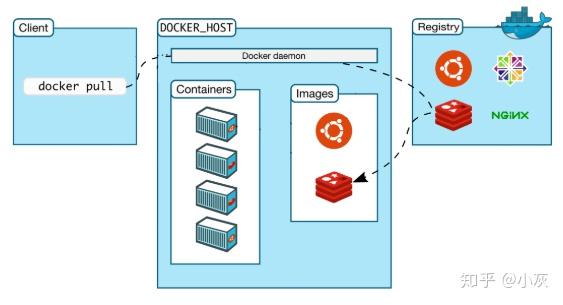
Docker 容器学习笔记
Docker 容器学习笔记 容器的由来 早先,虚拟机通过操作系统实现相互隔离,保证应用程序在运行时相互独立,避免相互干扰。但是操作系统又笨又重,耗费资源严重: 容器技术只隔离应用程序的运行时环境但容器之间共享同一个…...

Day03-vue基础
Day03-vue基础 一 列表渲染 v-for这个指令可以实现列表渲染 1 数组 <ul><!-- v-for遍历的时候,key必须赋唯一值第一个参数是数组元素,第二个参数是元素下标--><li v-for="(item,index) in [1,3,5,7]" :key="item">{{item}}--{{index}…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...
