【图论】缩点的综合应用(一)
一.缩点的概念
![]()
缩点,也称为点缩法(Vertex Contraction),是图论中的一种操作,通常用于缩小图的规模,同时保持了图的某些性质。这个操作的目标是将图中的一些节点合并为一个超级节点,同时调整相关边,以便保持图的连通性和其他性质。
具体步骤如下:
-
选择一个要缩点的节点:选择图中的一个节点,将它合并到另一个节点上。
-
合并节点:将选定的节点合并到另一个节点上,形成一个新的超级节点。通常情况下,选择入度或出度较小的节点进行合并,以减小新图的规模。
-
调整边:将与被合并节点相邻的边重新连接到新的超级节点上。注意要避免重复边和自环。
-
重复步骤1~3:继续选择节点进行缩点,直到不满足合并条件为止。
缩点操作通常用于算法设计和图分析中,有时可以用来简化图的复杂性,减少问题的规模。在一些情况下,缩点操作可能会破坏某些图的属性,因此在使用时需要谨慎考虑。此外,缩点操作后的图可能不再是原始问题的精确表示,可能会导致问题的近似解。
二.缩短的作用
把一个环缩为一个超级点,可以由有环图-->DAG,从而更好的解决问题。
总之就是我们不想要环,直接缩为一个点,我们可以更好地解决问题,就就可以使用缩点法。
三.模板题
P3387 【模板】缩点 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
四.思路
1.求点权之和最大,我们可以想到什么?最小生成树。
2.但这只需要解决一条路径的点权值最大,那可以怎么解决?拓扑+DP。
3.但是...拓扑只能解决DAG,这有环啊!!! 我们把环缩成一个超级点,然后再建一个新图不就行了吗?理论通过,实践开始!
五.实践
(1)tarjan缩点
主函数部分:
scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){scanf("%d",&p[i]);}for(int i=1;i<=m;i++){int u,v;scanf("%d%d",&u,&v);add(u,v);}for(int i=1;i<=n;i++){if(!dfn[i]) tarjan(i);}tarjan:
void tarjan(int u){dfn[u]=low[u]=++num;sta[++top]=u;ins[u]=1;for(int i=head[u];i;i=edge[i].next){int v=edge[i].v;if(!dfn[v]){tarjan(v);low[u]=min(low[u],low[v]);}else if(ins[v]){low[u]=min(low[u],dfn[v]);}}if(dfn[u]==low[u]){int j=0;while(1){j=sta[top--];ins[j]=0;h[j]=u; //j从此属于u if(j==u) break;p[u]+=p[j]; //点权值合并到第一个点(u点)上 }}
}(2)重新建图
for(int i=1;i<=m;i++){int u=h[edge[i].u],v=h[edge[i].v];if(u!=v){ //不在一个环 add2(u,v);in[v]++; //入度++,拓扑用 }}(3)拓扑排序+DP
int topu(){queue<int> q;for(int i=1;i<=n;i++){ if(!in[i] && i==h[i]){q.push(i); //这是这条路径的起点 dp[i]=p[i]; //记得赋值 } }//拓扑基础 while(!q.empty()){int k=q.front(); q.pop();for(int i=head2[k];i;i=ed[i].next){int v=ed[i].v;dp[v]=max(dp[v],dp[k]+p[v]);in[v]--;if(!in[v]) q.push(v);}}//找最大值,不一定n就最大,毕竟不止一条路 int ans=0;for(int i=1;i<=n;i++){ans=max(ans,dp[i]);}return ans;
}六.参考代码(完整代码)
#include<bits/stdc++.h>
#define maxn 100005
using namespace std;
int n,m;
int p[maxn];
struct Edge{int u,v,next;
}edge[maxn],ed[maxn];
int head[maxn],head2[maxn],cnt,cnt2;
void add(int u,int v){edge[++cnt]=(Edge){u,v,head[u]}; head[u]=cnt;
}
void add2(int u,int v){ed[++cnt2]=(Edge){u,v,head2[u]}; head2[u]=cnt2;
}
int dfn[maxn],low[maxn],num;
int sta[maxn],ins[maxn],top;
int lg,h[maxn]; //环的个数,成员属于哪个环
void tarjan(int u){dfn[u]=low[u]=++num;sta[++top]=u;ins[u]=1;for(int i=head[u];i;i=edge[i].next){int v=edge[i].v;if(!dfn[v]){tarjan(v);low[u]=min(low[u],low[v]);}else if(ins[v]){low[u]=min(low[u],dfn[v]);}}if(dfn[u]==low[u]){int j=0;while(1){j=sta[top--];ins[j]=0;h[j]=u; //j从此属于u if(j==u) break;p[u]+=p[j]; //点权值合并到第一个点(u点)上 }}
}
int in[maxn],dp[maxn];
int topu(){queue<int> q;for(int i=1;i<=n;i++){ if(!in[i] && i==h[i]){q.push(i); //这是这条路径的起点 dp[i]=p[i]; //记得赋值 } }//拓扑基础 while(!q.empty()){int k=q.front(); q.pop();for(int i=head2[k];i;i=ed[i].next){int v=ed[i].v;dp[v]=max(dp[v],dp[k]+p[v]);in[v]--;if(!in[v]) q.push(v);}}//找最大值,不一定n就最大,毕竟不止一条路 int ans=0;for(int i=1;i<=n;i++){ans=max(ans,dp[i]);}return ans;
}
int main(){scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){scanf("%d",&p[i]);}for(int i=1;i<=m;i++){int u,v;scanf("%d%d",&u,&v);add(u,v);}for(int i=1;i<=n;i++){if(!dfn[i]) tarjan(i);}for(int i=1;i<=m;i++){int u=h[edge[i].u],v=h[edge[i].v];if(u!=v){ //不在一个环 add2(u,v);in[v]++; //入度++,拓扑用 }}cout<<topu();return 0;
}相关文章:

【图论】缩点的综合应用(一)
一.缩点的概念 缩点,也称为点缩法(Vertex Contraction),是图论中的一种操作,通常用于缩小图的规模,同时保持了图的某些性质。这个操作的目标是将图中的一些节点合并为一个超级节点,同时调整相关…...

C++—纯虚函数
一、前言 定义一个函数为虚函数,不代表函数为不被实现的函数。 定义函数为虚函数是为了允许用基类的指针来调用子类的这个函数。 定义一个函数为纯虚函数,才代表函数没有被实现。 定义纯虚函数是为了实现一个接口,起到一个规范的作用&…...

经过卷积神经网络之后的图片的尺寸如何计算
经过卷积神经网络(Convolutional Neural Network,CNN)处理后,图片的尺寸会发生变化,这是由于卷积层、池化层等操作引起的。计算图片经过卷积神经网络后的尺寸变化通常需要考虑卷积核大小、步幅(stride&…...
,修改maven)
Java升级JDK17(更高版本同理),修改maven
记住三个网址就行:下面这个是oracle的 Java Platform, Standard Edition 17 ReferenceImplementations https://www.oracle.com/java/technologies/downloads/#jdk17-windows 另外一个 redhat旗下的:这个是开源的(推荐这个!&am…...
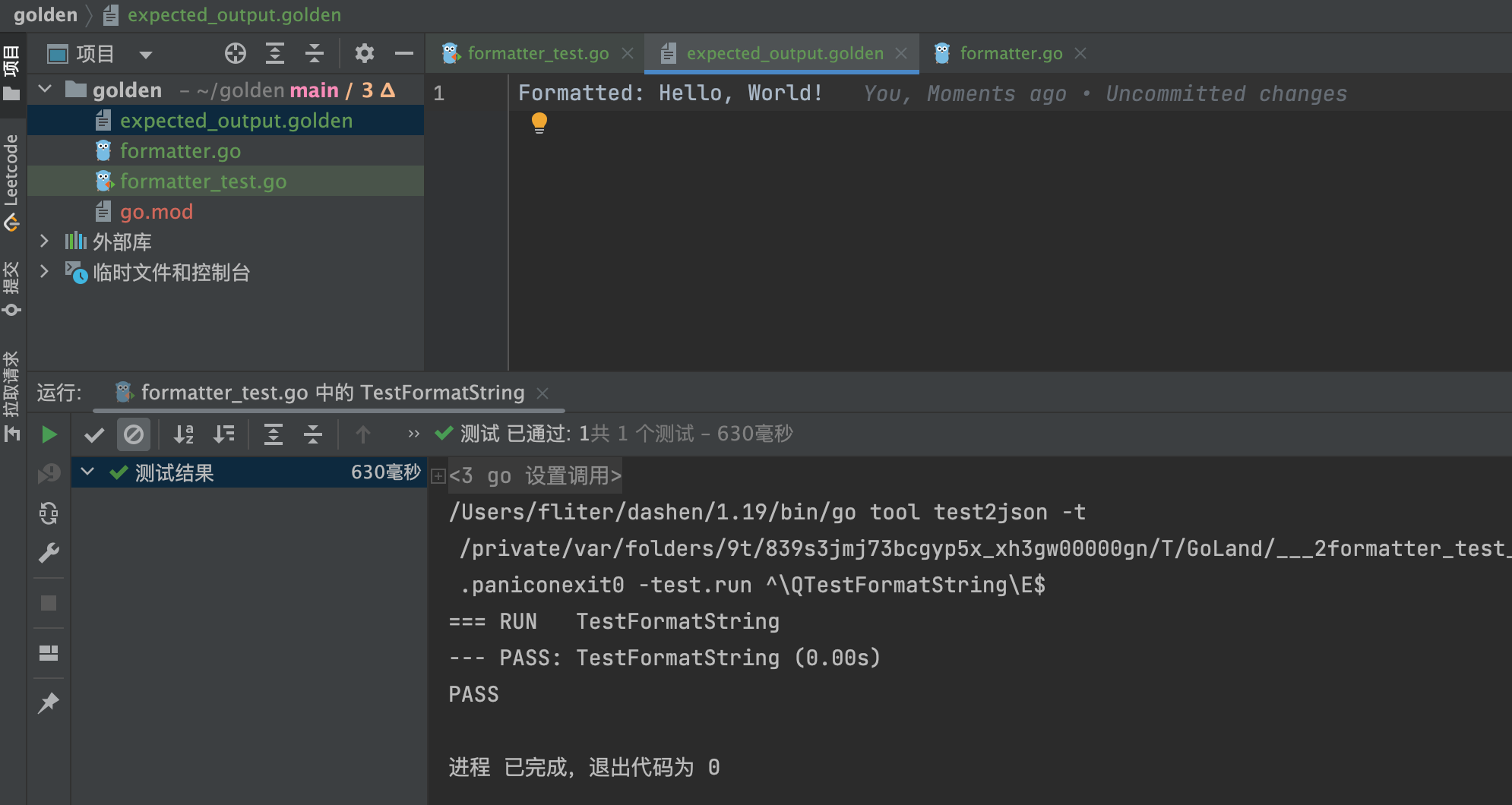
Go测试之.golden 文件
Go测试中的.golden 文件是干什么用的?请举例说明 在Go语言中,.golden文件通常用于测试中的黄金文件(golden files)。黄金文件是在测试期间记录预期输出结果的文件。测试用例运行时,黄金文件用于比较实际输出与预期输出…...

回归预测 | MATLAB实现GA-RF遗传算法优化随机森林算法多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现GA-RF遗传算法优化随机森林算法多输入单输出回归预测(多指标,多图) 目录 回归预测 | MATLAB实现GA-RF遗传算法优化随机森林算法多输入单输出回归预测(多指标,多图)效果一览基本介绍程…...
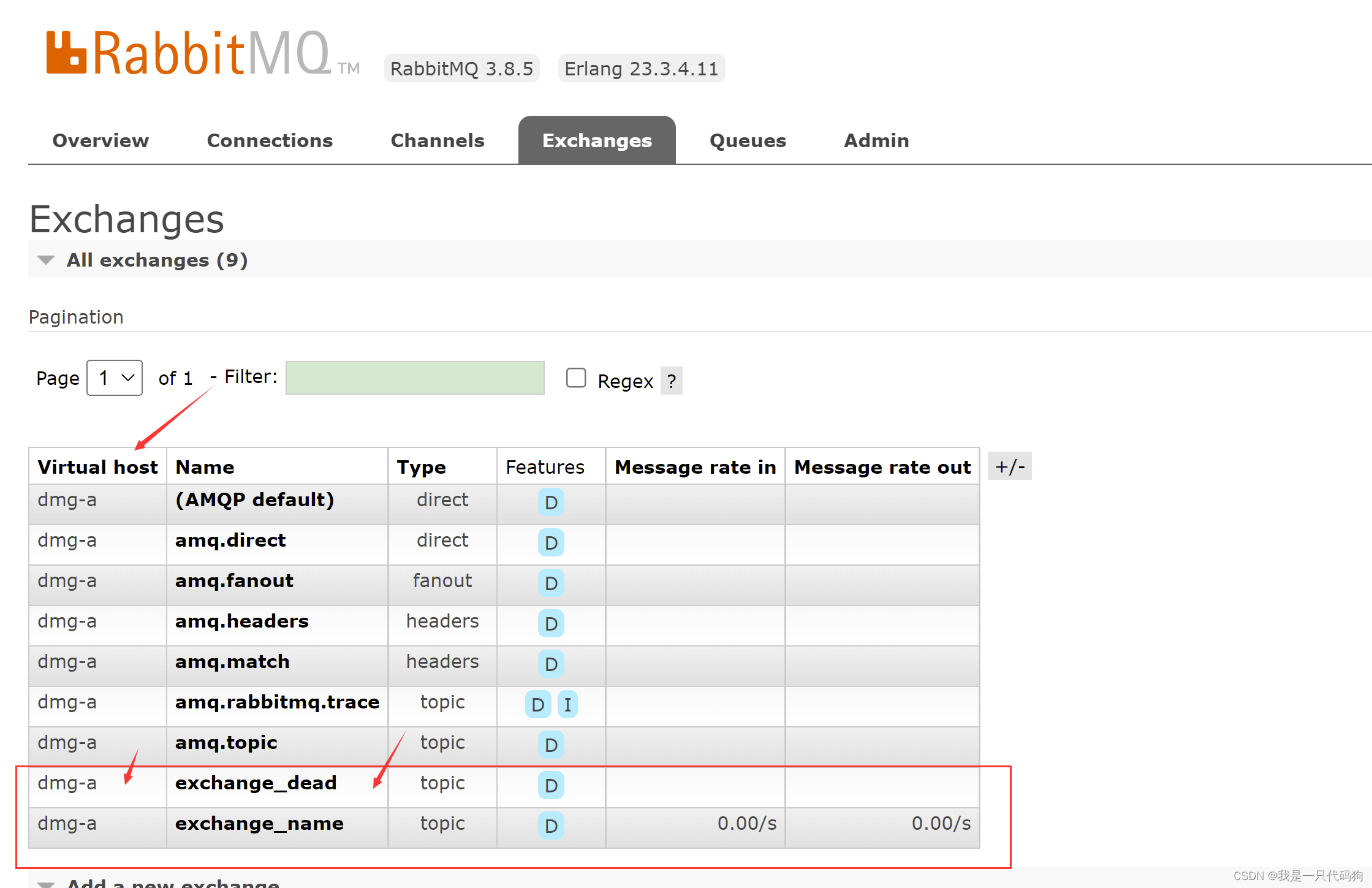
springboot整合rabbitmq死信队列
springboot整合rabbitmq死信队列 什么是死信 说道死信,可能大部分观众大姥爷会有懵逼的想法,什么是死信?死信队列,俗称DLX,翻译过来的名称为Dead Letter Exchange 死信交换机。当消息限定时间内未被消费,…...
高中信息技术教资考试模拟卷(22下)
2022 年下半年全国教师资格考试模考卷一 (高中信息技术) 一、单项选择题(本大题共 15 小题,每小题 3 分,共 45 分) 1.2006 年 10 月 25 日,深圳警方成功解救出一名被网络骗子孙某…...

Linux中shadow及passwd格式内容解析
/etc/passwd文件包括Linux账号信息,示例如下: root:x:0:0:root:/root:/bin/bash bin:x:1:1:bin:/bin:/sbin/nologin daemon:x:2:2:daemon:/sbin:/sbin/nologin adm:x:3:4:adm:/var/adm:/sbin/nologin 具体格式 用户名࿱…...

计算机视觉 – Computer Vision | CV
计算机视觉为什么重要? 人的大脑皮层, 有差不多 70% 都是在处理视觉信息。 是人类获取信息最主要的渠道,没有之一。 在网络世界,照片和视频(图像的集合)也正在发生爆炸式的增长! 下图是网络上…...
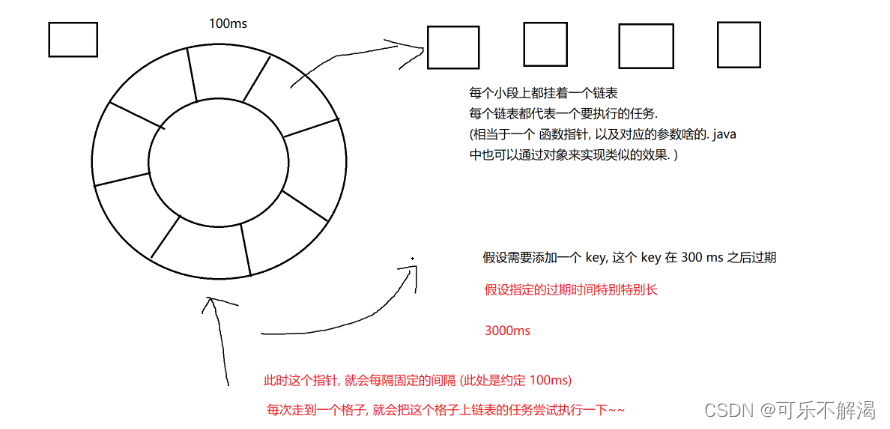
2.Redis 通用命令
Redis 中最核心的两个命令: set 作用:设置 key 对应的 value 值并存储进去。若key已包含一个值,则无论其类型如何,都会覆盖该值。在SET操作成功时,将丢弃与密钥相关联的任何先前生存时间。 对于上述这里的 key和val…...

【学习FreeRTOS】第18章——FreeRTOS软件定时器
1.软件定时器的简介 定时器:从指定的时刻开始,经过一个指定时间,然后触发一个超时事件,用户可自定义定时器的周期硬件定时器:芯片本身自带的定时器模块,硬件定时器的精度一般很高,每次在定时时…...

C++--两个数组的dp问题(2)
1.交错字符串 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 给定三个字符串 s1、s2、s3,请判断 s3 能不能由 s1 和 s2 交织(交错) 组成。 两个字符串 s 和 t 交织 的定义与过程如下,其中每个字符串都…...

利用人工智能彻底改变库存管理:综合指南
通过本指南了解人工智能如何增强库存管理,为希望简化运营的管理者和企业主提供帮助。 库存管理是任何销售实物产品的企业的重要组成部分。它包括跟踪库存水平,预测未来需求,并确保始终有足够的产品来满足客户需求,但又不会因库存过多而浪费金钱。有效的库存管理可以显着降…...

连接器信号完整性仿真教程 七
本将介绍微带线及差分微带线仿真。做连接器信号完整性仿真时,有时后没法将激励端口直接设置到连接器端子上,这就需画出连接器PCB PAD,将激励端口设置在PAD的端面上,或者用引线连接PAD,将引线引出到适当的位置ÿ…...
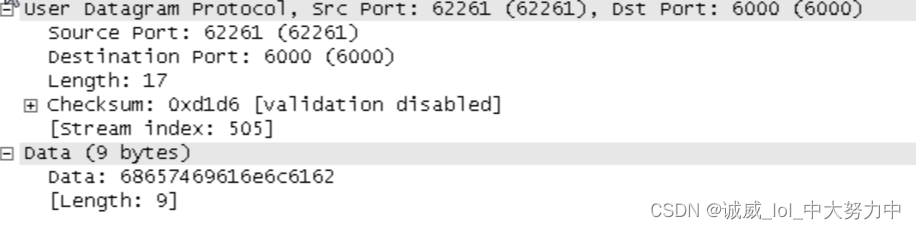
Wireshark数据抓包分析之UDP协议
一、实验目的: 通过使用wireshark对UDP数据包的抓取分析UDP协议的内容 二、预备知识: UDP协议的概念:UDP使用底层的互联网协议来传送报文,同IP一样提供不可靠的无连接传输服务。它也不提供报文到达确认、排序及流量控制等功能。 …...
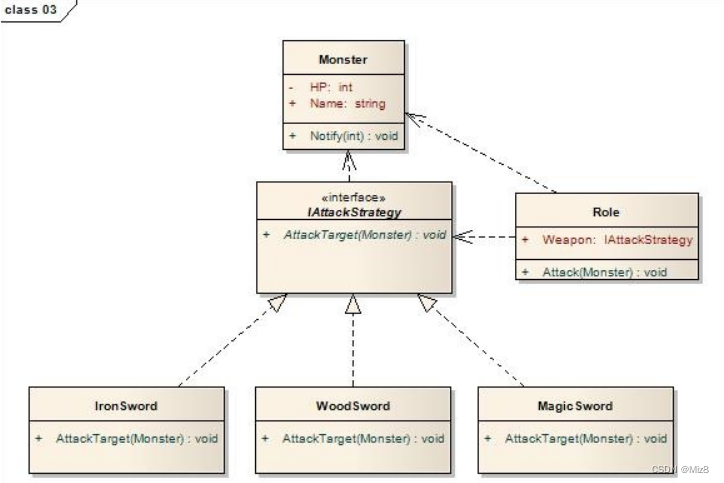
Java小游戏
一、需求 二、思路一 HP当然是怪物的一个属性成员,而武器是角色的一个属性成员,类型可以使字符串,用于描述目前角色所装备的武器。角色类有一个攻击方法,以被攻击怪物为参数,当实施一次攻击时,攻击方法被调…...
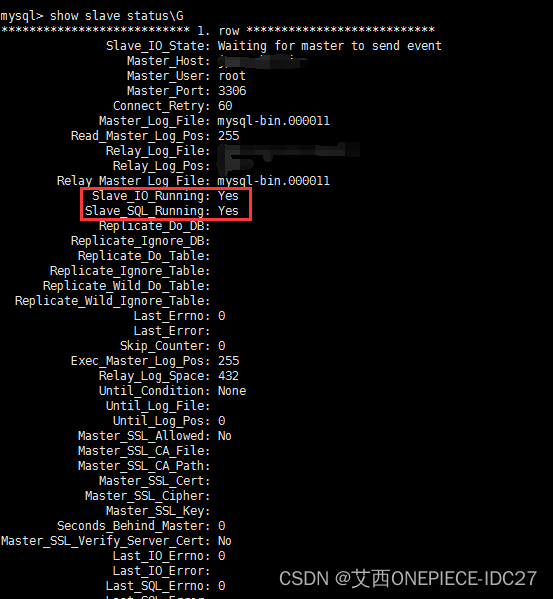
服务器Linux系统配置mysql数据库主从自动备份
服务器Linux系统配置mysql数据库主从自动备份 当数据内容越来越多的时候,数据库也变得越来越大了。如果不小心误删了,或者被黑主机了,那就什么都没有了。所以数据库的数据怎么能让它不丢失做到万无一失变得尤为重要! 我是艾西&a…...

Java通过PowerMockito和Mokito进行单元测试
PowerMockito和Mokito的概念 PowerMockito和Mockito都是Java语言中的测试框架,用于进行单元测试和集成测试。它们中的每一个都有不同的功能和应用。 Mockito是一个基于模拟的测试框架。它允许你模拟对象,在测试中隔离被测代码的依赖项。使用Mockito&am…...
数字化技术无限延伸,VR全景点亮智慧生活
随着互联网的发展,我们无时无刻不再享受着互联网给我们带来的便利,数字化生活正在无限延伸,各行各业也开始积极布局智能生活。要说智慧生活哪个方面应用的比较多,那应该就是VR全景了,目前VR全景已经被各个行业广泛应用…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章
用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章 摘要: 操作系统内核的安全性、稳定性至关重要。传统 Linux 内核模块开发长期依赖于 C 语言,受限于 C 语言本身的内存安全和并发安全问题,开发复杂模块极易引入难以…...
深入理解 C++ 左值右值、std::move 与函数重载中的参数传递
在 C 编程中,左值和右值的概念以及std::move的使用,常常让开发者感到困惑。特别是在函数重载场景下,如何合理利用这些特性来优化代码性能、确保语义正确,更是一个值得深入探讨的话题。 在开始之前,先提出几个问题&…...
——Oracle for Linux物理DG环境搭建(2))
Oracle实用参考(13)——Oracle for Linux物理DG环境搭建(2)
13.2. Oracle for Linux物理DG环境搭建 Oracle 数据库的DataGuard技术方案,业界也称为DG,其在数据库高可用、容灾及负载分离等方面,都有着非常广泛的应用,对此,前面相关章节已做过较为详尽的讲解,此处不再赘述。 需要说明的是, DG方案又分为物理DG和逻辑DG,两者的搭建…...
