统计学补充概念-17-线性决策边界
概念
线性决策边界是一个用于分类问题的线性超平面,可以将不同类别的样本分开。在二维空间中,线性决策边界是一条直线,将两个不同类别的样本分隔开来。对于更高维的数据,决策边界可能是一个超平面。
线性决策边界的一般形式可以表示为:


在训练分类模型时,目标是找到合适的权重和偏置项,使得决策边界能够最好地将不同类别的样本分开。一些机器学习算法,如逻辑回归、支持向量机等,就是在不同约束和优化目标下寻找合适的决策边界参数。
代码实现
import numpy as np
import matplotlib.pyplot as plt# 生成虚拟数据集
np.random.seed(42)
X = np.random.randn(100, 2)
y = (X[:, 0] + X[:, 1] > 0).astype(int)# 将类别0和类别1的样本分开
X_class0 = X[y == 0]
X_class1 = X[y == 1]# 绘制散点图
plt.figure(figsize=(10, 6))
plt.scatter(X_class0[:, 0], X_class0[:, 1], c='b', label='Class 0')
plt.scatter(X_class1[:, 0], X_class1[:, 1], c='r', label='Class 1')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')# 绘制线性决策边界
x_boundary = np.linspace(X[:, 0].min(), X[:, 0].max(), 100)
y_boundary = -x_boundary # 决策边界的直线方程为 x + y = 0
plt.plot(x_boundary, y_boundary, 'k--', label='Decision Boundary')plt.legend()
plt.title("Linear Decision Boundary")
plt.show()相关文章:

统计学补充概念-17-线性决策边界
概念 线性决策边界是一个用于分类问题的线性超平面,可以将不同类别的样本分开。在二维空间中,线性决策边界是一条直线,将两个不同类别的样本分隔开来。对于更高维的数据,决策边界可能是一个超平面。 线性决策边界的一般形式可以表…...

指针变量、指针常量与常量指针的区别
指针变量、指针常量与常量指针 一、指针变量 定义:指针变量是指存放地址的变量,其值是地址。 一般格式:基类型 指针变量名;(int p) 关键点: 1、int * 表示一种指针类型(此处指int 类型),p(变量…...
mq与mqtt的关系
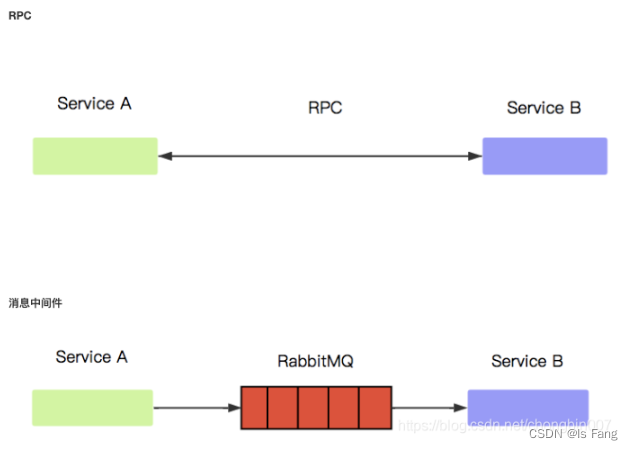
文章目录 mqtt 与 mq的区别mqtt 与 mq的详细区别传统消息队列RocketMQ和微消息队列MQTT对比:MQ与RPC的区别 mqtt 与 mq的区别 mqtt:一种通信协议,规范 MQ:一种通信通道(方式),也叫消息队列 MQ…...
)
代码大全阅读随笔 (二)
软件设计 设计就是把需求分析和编码调试连在一起的活动。 设计不是在谁的头脑中直接跳出来了,他是不断的设计评估,非正式讨论,写实验代码以及修改实验代码中演化和完善。 作为软件开发人员,我们不应该试着在同一时间把整个程序都塞…...

vue 项目的屏幕自适应方案
方案一:使用 scale-box 组件 属性: width 宽度 默认 1920height 高度 默认 1080bgc 背景颜色 默认 "transparent"delay自适应缩放防抖延迟时间(ms) 默认 100 vue2版本:vue2大屏适配缩放组件(vu…...

23软件测试高频率面试题汇总
一、 你们的测试流程是怎么样的? 答:1.项目开始阶段,BA(需求分析师)从用户方收集需求并将需求转化为规格说明书,接 下来在项目组领导会组织需求评审。 2.需求评审通过后,BA 会组织项目经理…...

PHP8的匿名函数-PHP8知识详解
php 8引入了匿名函数(Anonymous Functions),它是一种创建短生命周期的函数,不需要命名,并且可以在其作用域内直接使用。以下是在PHP 8中使用匿名函数的知识要点: 1、创建匿名函数,语法格式如下&…...

Redis—Redis介绍(是什么/为什么快/为什么做MySQL缓存等)
一、Redis是什么 Redis 是一种基于内存的数据库,对数据的读写操作都是在内存中完成,因此读写速度非常快,常用于缓存,消息队列、分布式锁等场景。 Redis 提供了多种数据类型来支持不同的业务场景,比如 String(字符串)、…...
C语言链表梳理-2
链表头使用结构体:struct Class 链表中的每一项使用结构体:struct Student#include <stdio.h>struct Student {char * StudentName;int StudentAge;int StudentSex;struct Student * NextStudent; };struct Class {char *ClassName;struct Stude…...
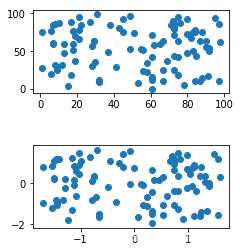
【深度学习】实验03 特征处理
文章目录 特征处理标准化归一化正则化 特征处理 标准化 # 导入标准化库 from sklearn.preprocessing import StandardScalerfrom matplotlib import gridspec import numpy as np import matplotlib.pyplot as plt import warnings warnings.filterwarnings("ignore&quo…...

基于Dpabi的功能连接
1.预处理 这里预处理用Gretna软件进行,共分为以下几步: (1)DICOM转NIfTI格式 (2)去除前10个时间点(Remove first 10 times points):由于机器刚启动、被试刚躺进去也还需适应环境,导致刚开始扫描的数据很…...

在React项目是如何捕获错误的?
文章目录 react中的错误介绍解决方案后言 react中的错误介绍 错误在我们日常编写代码是非常常见的 举个例子,在react项目中去编写组件内JavaScript代码错误会导致 React 的内部状态被破坏,导致整个应用崩溃,这是不应该出现的现象 作为一个框架…...

基于内存池的 简单高效的数据库 SDK简介
基于内存池的 简单高效的数据库 SDK简介 下载地址: https://gitee.com/tankaishuai/powerful_sdks/tree/master/shm_alloc_db_heap shm_alloc_db_heap 是一个基于内存池实现的简单高效的文件型数据存储引擎,利用它可以轻松地像访问内存块一样读、写、增…...
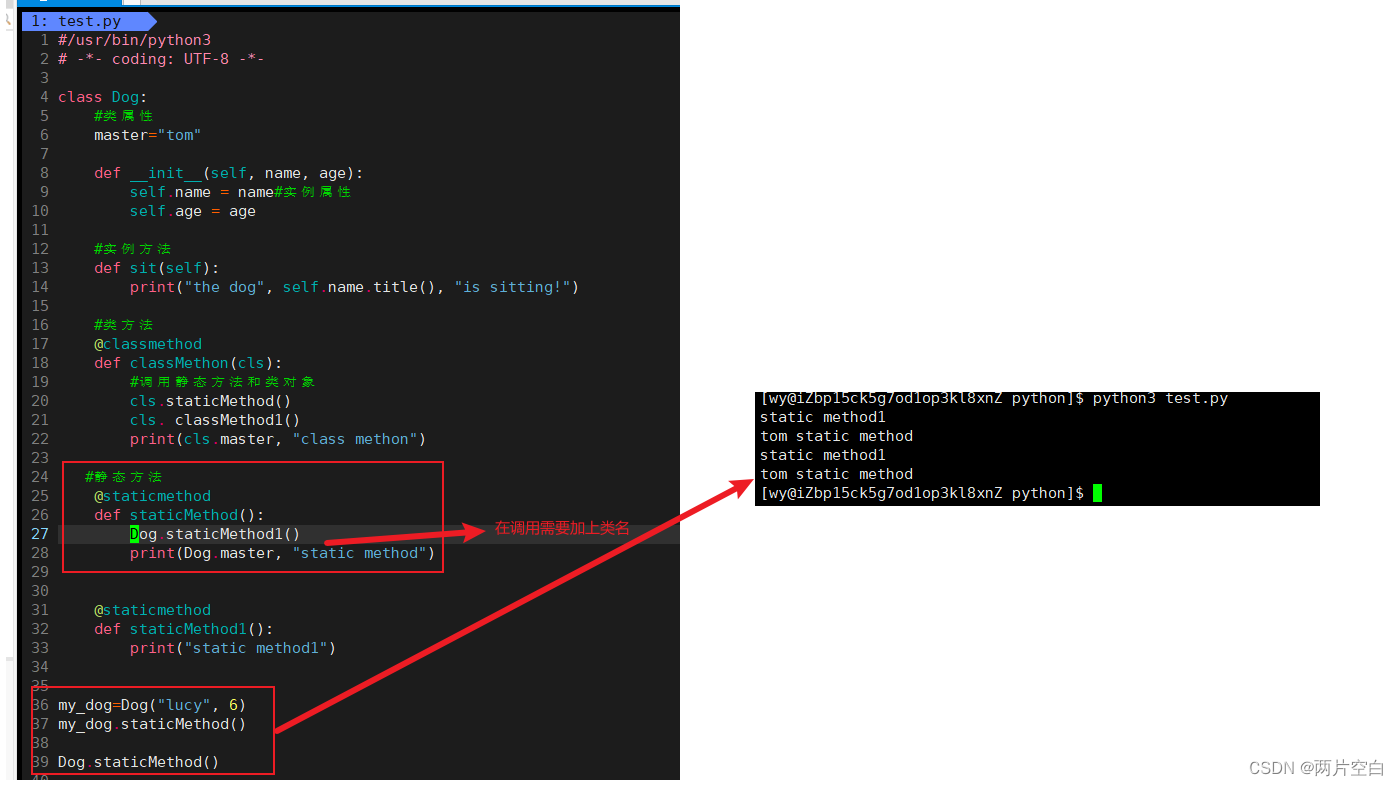
python实例方法,类方法和静态方法区别
为python中的装饰器 实例方法 实例方法时直接定义在类中的函数,不需要任何修饰。只能通过类的实例化对象来调用。不能通过类名来调用。 类方法 类方法,是类中使用classmethod修饰的函数。类方法在定义的时候需要有表示类对象的参数(一般命名为cls&#…...
:使用pyecharts绘制3D折线图)
Pyecharts教程(四):使用pyecharts绘制3D折线图
Pyecharts教程(四):使用pyecharts绘制3D折线图 作者:安静到无声 个人主页 目录 Pyecharts教程(四):使用pyecharts绘制3D折线图准备工作数据准备绘制3D折线图推荐专栏在这篇文章中,我们将学习如何使用pyecharts库来绘制一个3D折线图。pyecharts是一个用于生成Echarts图表的…...
【stable-diffusion使用扩展+插件和模型资源(下)】
插件模型魔法图片等资源:https://tianfeng.space/1240.html 书接上文:(上) 插件推荐 1.lobe theme lobe theme是一款主题插件,直接可以在扩展安装 界面进行了重新布局,做了一些优化,有兴趣的…...

一文了解SpringBoot中的Aop
目录 1.什么是Aop 2.相关概念 3.相关注解 4.为什么要用Aop 5.Aop使用案例 1.什么是Aop AOP:Aspect Oriented Programming,面向切面,是Spring三大思想之一,另外两个是 IOC-控制反转 DI-依赖注入 (Autowired、Qualifier、Re…...
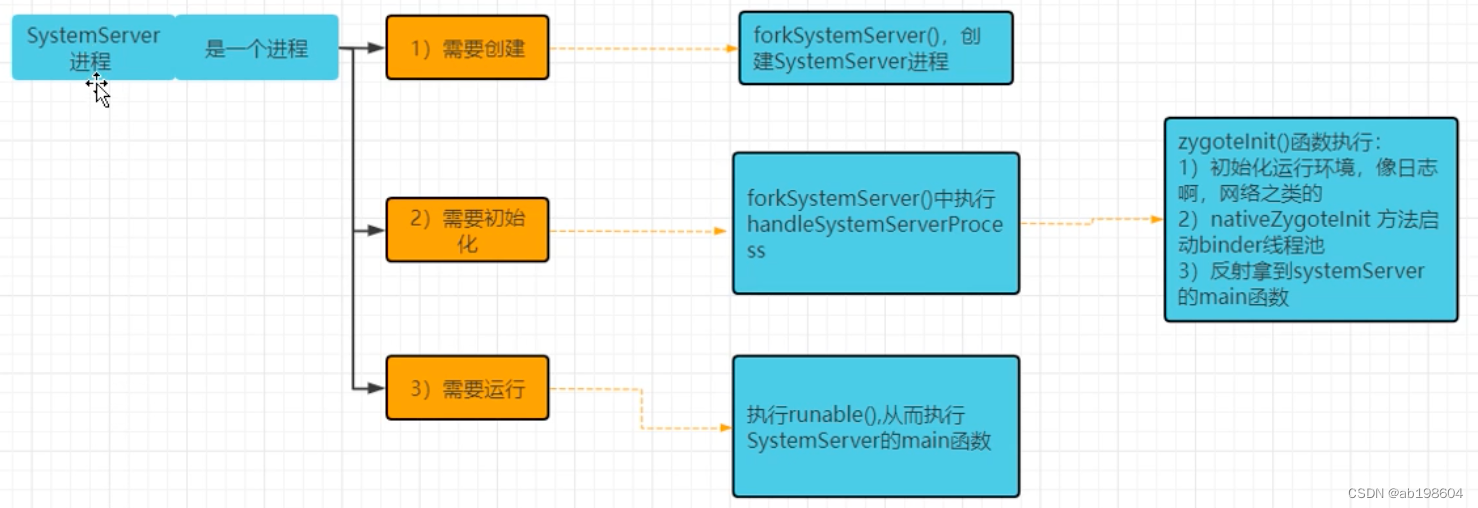
android系统启动流程之zygote如何创建SystemServer进程
SystemServer:是独立的进程,主要工作是管理服务的,它将启动大约90种服务Services. 它主要承担的职责是为APP的运行提供各种服务,像AMS,WMS这些服务并不是一个独立的进程, 它们其实都是SystemServer进程中需要管理的的众多服务之一…...
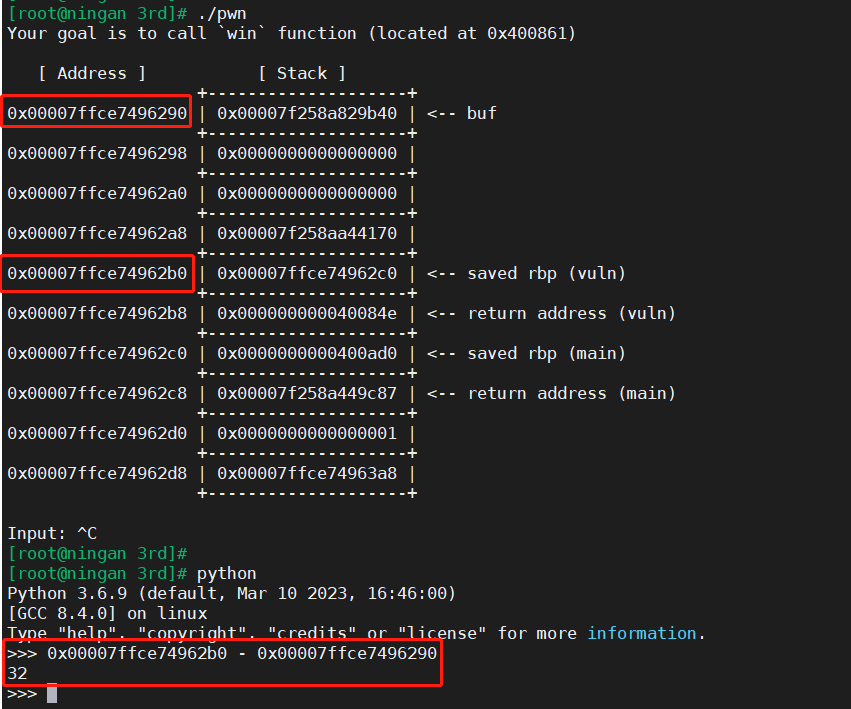
【awd系列】Bugku S3 AWD排位赛-9 pwn类型
文章目录 二进制下载检查分析运行二进制ida分析解题思路exp 二进制下载 下载地址:传送门 检查分析 [rootningan 3rd]# file pwn pwn: ELF 64-bit LSB executable, x86-64, version 1 (SYSV), dynamically linked, interpreter /lib64/ld-linux-x86-64.so.2, for …...

vcomp140.dll丢失的修复方法分享,电脑提示vcomp140.dll丢失修复方法
今天,我的电脑出现了一个奇怪的问题,打开某些程序时总是提示“找不到vcomp140.dll文件”。这个问题让我非常头疼,因为我无法正常使用电脑上的一些重要软件。为了解决这个问题,我在网上查找了很多资料,并尝试了多种方法…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...
