Springboot+Mybatis框架是否会取代SSM框架?
个人认真思考的观点:从市场使用来说,会有这个趋势。从技术上来说,不存在被替代这一说。
Spring Boot+Mybatis框架是指使用Spring Boot作为基础框架,并集成Mybatis作为持久层框架的组合,它是一个基于Spring框架的快速开发工具,可以简化Spring应用的创建和配置 。
SSM框架是指Spring+Spring MVC+Mybatis三个框架的组合,它是一个传统的Java Web开发框架,可以实现Web层、业务层和持久层的分离和整合 。
从技术上来说,Spring Boot+Mybatis框架并没有取代SSM框架,而是在SSM框架的基础上提供了更多的便利和功能,让我们可以更专注于业务逻辑的开发,而不是基础设施的搭建 。Spring Boot+Mybatis框架仍然使用了Spring MVC和Mybatis作为Web层和持久层的框架,只是使用了Spring Boot来自动配置和管理它们,而不需要手动的去整合和配置 。
从市场上来说,Spring Boot+Mybatis框架可能会逐渐替代SSM框架,因为它具有更高的开发效率和更低的学习成本,可以满足大多数项目的需求 。随着Spring Boot+Mybatis框架的普及和完善,越来越多的企业和开发者会选择使用这个框架来构建应用,而SSM框架可能会逐渐被边缘化或淘汰 。
根据[2020年中国Java开发者调查报告],Spring Boot+Mybatis框架是目前最受欢迎的Java Web开发框架,占据了48.7%的市场份额,远超过其他框架组合,如SSM(Spring+Spring MVC+Mybatis)、SSH(Spring+Struts+Hibernate)等。这说明Spring Boot+Mybatis框架在企业开发中具有很高的流行度和认可度 。
综上所述,Spring Boot+Mybatis框架并没有从技术上取代SSM框架,而是在其基础上提供了更多的优势和特性,但从市场上来看,Spring Boot+Mybatis框架可能会逐渐替代SSM框架,成为主流的Java Web开发框架。
相关文章:

Springboot+Mybatis框架是否会取代SSM框架?
个人认真思考的观点:从市场使用来说,会有这个趋势。从技术上来说,不存在被替代这一说。 Spring BootMybatis框架是指使用Spring Boot作为基础框架,并集成Mybatis作为持久层框架的组合,它是一个基于Spring框架的快速开发…...

使用windeployqt和InstallShield打包发布Qt软件的流程
前言 Qt编译之后需要打包发布,并且发布给用户后需要增加一个安装软件,通过安装软件可以实现Qt软件的安装;用于安装软件的软件有很多,这里主要介绍InstallShield使用的流程; 使用windeployqt打包Qt编译后的程序 Qt程序…...
方法阻塞问题)
解决selenium的getdrive()方法阻塞问题
selenium里面的Webdriver的get()方法默认是阻塞的,也就是说要等整个页面全都加载完它才会相应。但我们大部分时候不需要用到页面里的所有东西,也许只需要用到里面的一个元素就行了 所以下面是我的解决方法: 初始化代码: # 设置…...

js的闭包
闭包是有权限访问其他函数作用域的局部变量的一个函数 代码 function outer(){const a1;function f(){console.log(a)}f()}outer() 简单来说:闭包内层函数引用的外层函数变量 为什么要使用闭包? 用此方法可以来统计函数调用次数, 但是如…...
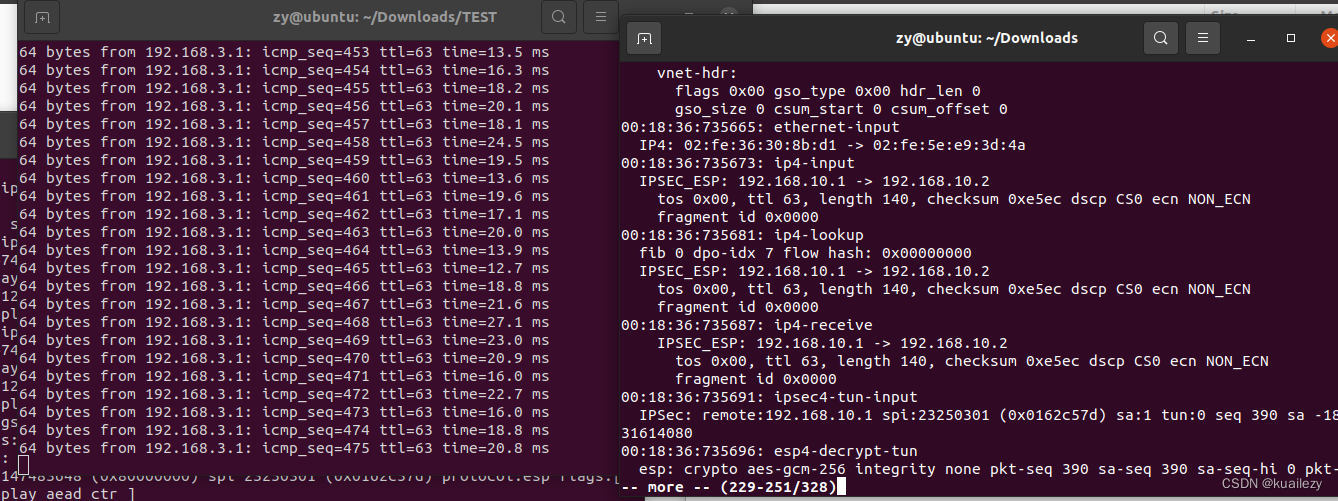
ubuntu20.04 直接安装vpp23.06 测试双 VPP Tunnel Ike2
环境信息:VMware Workstation 17 Pro ubuntu20.04 (清华源) ubuntu 源点进去选:ubuntu-22.04.3-desktop-amd64.iso 如果之前装过VPP,用以下命令确定是否卸载干净: dpkg -l | grep vpp dpkg -l | grep DPDK 卸载: …...

mysql sql 执行流程
监控查询缓存的命中率 show status like ‘%qcache%’; mysql 缓存机制,以及 8.0 为啥取消 select sql_NO_Cache * from 表 where xxx; # 不使用缓存...

go-kafka
go kafka包 本文使用的是kafka-go 6.5k 这个包 其他包参考: 我们在细分市场中非常依赖GO和Kafka。不幸的是,在撰写本文时,Kafka的GO客户库的状态并不理想。可用选项是: 萨拉玛(Sarama) 10k,这…...
如何在windows电脑上安装多个node,并可以进行随意切换
一、进入官网http://nvm.uihtm.com/ 下载 二、启动解压后的程序 1.开始安装nvm 选择要安装的目录 一直下一步–下一步–最后点击完成 3.最后点击完成即可 
《机器学习核心技术》分类算法 - 决策树
「作者主页」:士别三日wyx 「作者简介」:CSDN top100、阿里云博客专家、华为云享专家、网络安全领域优质创作者 「推荐专栏」:小白零基础《Python入门到精通》 决策树 1、决策树API2、决策时实际应用2.1、获取数据集2.2、划分数据集2.3、决策…...
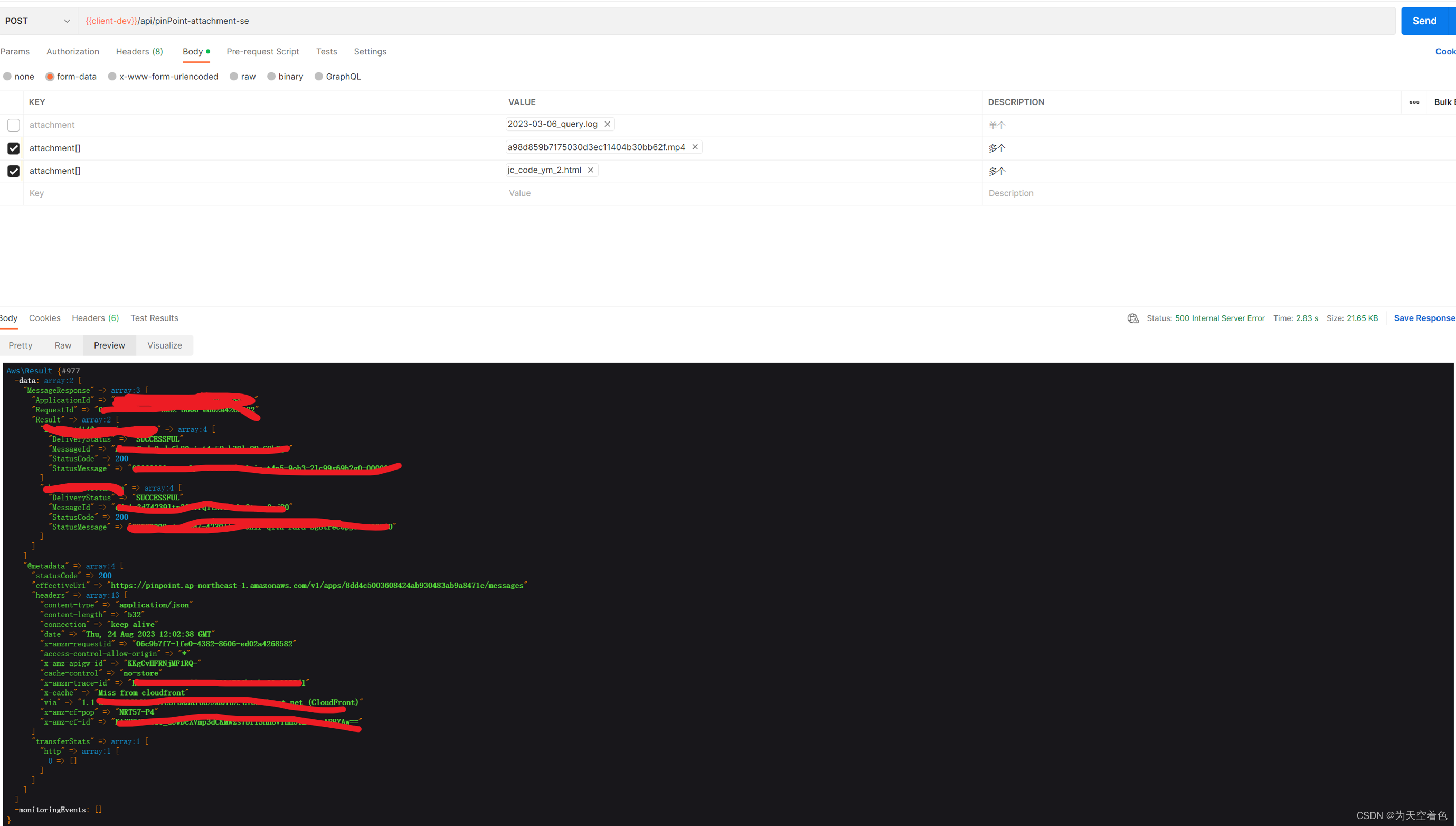
aws PinPoint发附件demo
php 版aws PinPoint发附件demo Laravel8框架,安装了"aws/aws-sdk-php": "^3.257" 主要代码: public function sendRawMail(Request $request) {$file $request->file(attachment);/*echo count($file);dd($file);*/$filenam…...
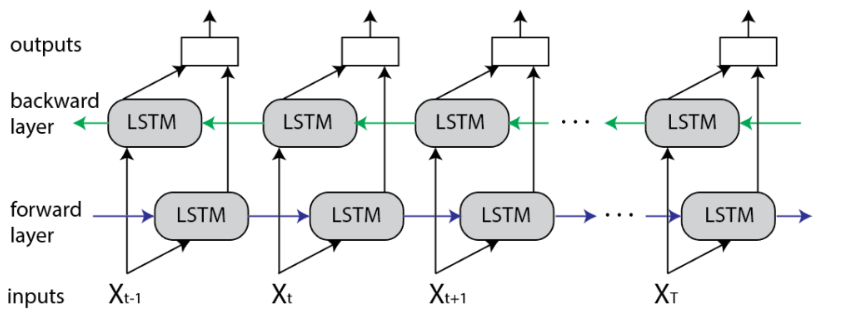
边写代码边学习之Bidirectional LSTM
1. 什么是Bidirectional LSTM 双向 LSTM (BiLSTM) 是一种主要用于自然语言处理的循环神经网络。 与标准 LSTM 不同,输入是双向流动的,并且它能够利用双方的信息。 它也是一个强大的工具,可以在序列的两个方向上对单词和短语之间的顺序依赖…...

Django学习笔记-实现联机对战
笔记内容转载自 AcWing 的 Django 框架课讲义,课程链接:AcWing Django 框架课。 CONTENTS 1. 统一长度单位2. 增加联机对战模式3. 配置Django Channels 1. 统一长度单位 多人模式中每个玩家所看到的地图相对来说应该是一样的,因此需要固定地…...
nacos总结1
5.Nacos注册中心 国内公司一般都推崇阿里巴巴的技术,比如注册中心,SpringCloudAlibaba也推出了一个名为Nacos的注册中心。 5.1.认识和安装Nacos Nacos是阿里巴巴的产品,现在是SpringCloud中的一个组件。相比Eureka功能更加丰富,…...
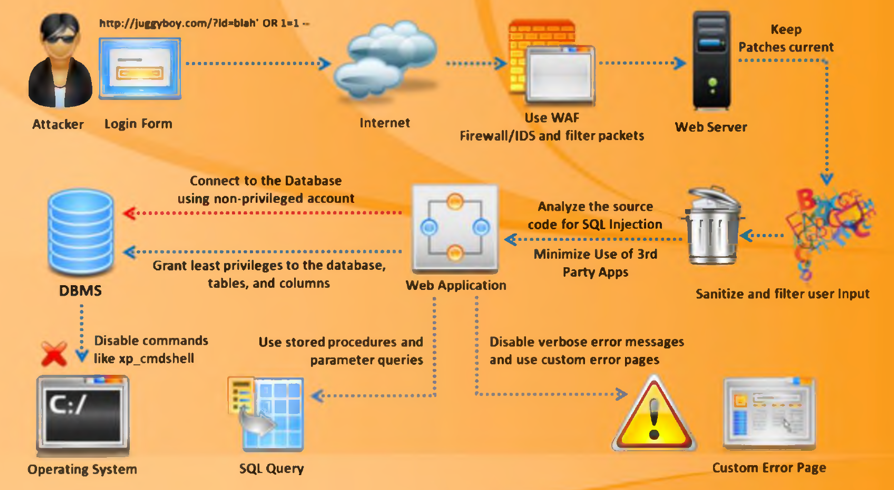
Web安全测试(三):SQL注入漏洞
一、前言 结合内部资料,与安全渗透部门同事合力整理的安全测试相关资料教程,全方位涵盖电商、支付、金融、网络、数据库等领域的安全测试,覆盖Web、APP、中间件、内外网、Linux、Windows多个平台。学完后一定能成为安全大佬! 全部…...
Webstorm 入门级玩转uni-app 项目-微信小程序+移动端项目方案
1. Webstorm uni-app语法插件 : Uniapp Support Uniapp Support - IntelliJ IDEs Plugin | Marketplace 第一个是不收费,第二个收费 我选择了第二个Uniapp Support ,有试用30天,安装重启webstorm之后,可以提高生产率…...
| 集群分发脚本xsync)
从零开始的Hadoop学习(三)| 集群分发脚本xsync
1. Hadoop目录结构 bin目录:存放对Hadoop相关服务(hdfs,yarn,mapred)进行操作的脚本etc目录:Hadoop的配置文件目录,存放Hadoop的配置文件lib目录:存放Hadoop的本地库(对…...

golang http transport源码分析
golang http transport源码分析 前言 Golang http库在日常开发中使用会很多。这里通过一个demo例子出发,从源码角度梳理golang http库底层的数据结构以及大致的调用流程 例子 package mainimport ("fmt""net/http""net/url""…...
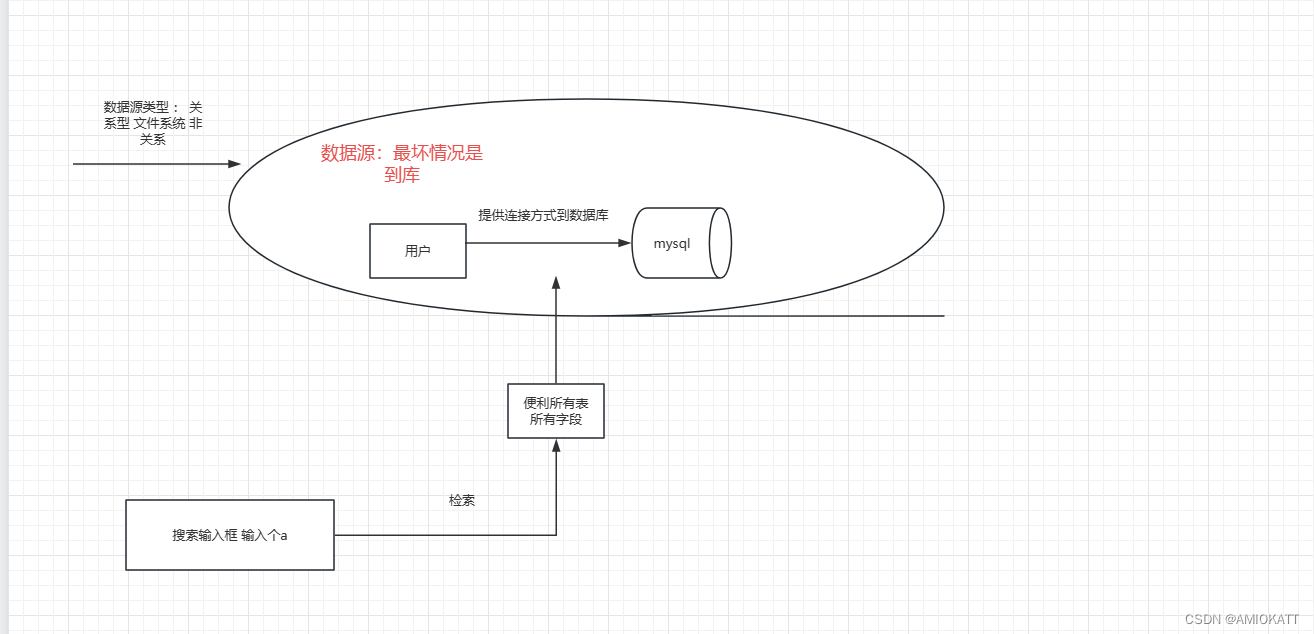
spring boot 项目整合 websocket
1.业务背景 负责的项目有一个搜索功能,搜索的范围几乎是全表扫,且数据源类型贼多。目前对搜索的数据量量级未知,但肯定不会太少,不仅需要搜索还得点击下载文件。 关于搜索这块类型 众多,未了避免有个别极大数据源影响整…...

统计学补充概念-17-线性决策边界
概念 线性决策边界是一个用于分类问题的线性超平面,可以将不同类别的样本分开。在二维空间中,线性决策边界是一条直线,将两个不同类别的样本分隔开来。对于更高维的数据,决策边界可能是一个超平面。 线性决策边界的一般形式可以表…...

指针变量、指针常量与常量指针的区别
指针变量、指针常量与常量指针 一、指针变量 定义:指针变量是指存放地址的变量,其值是地址。 一般格式:基类型 指针变量名;(int p) 关键点: 1、int * 表示一种指针类型(此处指int 类型),p(变量…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
