三、NetworkX工具包实战3——特征工程【CS224W】(Datawhale组队学习)
开源内容:https://github.com/TommyZihao/zihao_course/tree/main/CS224W
子豪兄B 站视频:https://space.bilibili.com/1900783/channel/collectiondetail?sid=915098
斯坦福官方课程主页:https://web.stanford.edu/class/cs224w
NetworkX主页:https://networkx.org
nx.Graph :https://networkx.org/documentation/stable/reference/classes/graph.html#networkx.Graph
给图、节点、连接添加属性:https://networkx.org/documentation/stable/tutorial.html#attributes
读写图:https://networkx.org/documentation/stable/reference/readwrite/index.html
文章目录
- PageRank节点重要度
- 节点连接数Node Degree度分析¶
- 最大连通域子图
- 节点的连接数可视化
- 棒棒糖图特征分析
- 图数据分析
- 每两个节点之间的最短距离
- 不同距离的节点对个数
- 计算节点特征
- 可视化辅助函数
- Node Degree
- 节点重要度特征 Centrality
- Degree Centrality
- Eigenvector Centrality
- Betweenness Centrality(必经之地)
- Closeness Centrality(去哪儿都近)
- PageRank
- Katz Centrality
- HITS Hubs and Authorities
- 社群属性 Clustering
- 三角形个数
- Clustering Coefficient
- Bridges
- Common Neighbors 、Jaccard Coefficient和Adamic-Adar index
- Katz Index
- 计算全图Graphlet个数
- 指定Graphlet
- 匹配Graphlet,统计个数
- 拉普拉斯矩阵特征值分解
- 拉普拉斯矩阵(Laplacian Matrix)
- 归一化拉普拉斯矩阵(Normalized Laplacian Matrix)
- 特征值分解
- 特征值分布直方图
- 北京上海地铁站图数据挖掘
- Shortest Path 最短路径
- 地图导航系统
- 总结
PageRank节点重要度
在NetworkX中,计算有向图节点的PageRank节点重要度。
# 图数据挖掘
import networkx as nx# 数据可视化
import matplotlib.pyplot as plt
%matplotlib inlineplt.rcParams['font.sans-serif']=['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False # 用来正常显示负号
G = nx.star_graph(7)
nx.draw(G, with_labels = True)
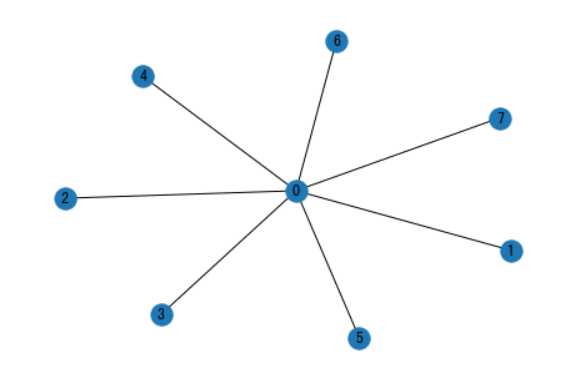
pagerank = nx.pagerank(G, alpha=0.8)
pagerank
{0: 0.4583348922684132,
1: 0.07738072967594098,
2: 0.07738072967594098,
3: 0.07738072967594098,
4: 0.07738072967594098,
5: 0.07738072967594098,
6: 0.07738072967594098,
7: 0.07738072967594098}
节点连接数Node Degree度分析¶
在NetworkX中,计算并统计图中每个节点的连接数Node Degree,绘制可视化和直方图。
# 图数据挖掘
import networkx as nximport numpy as np# 数据可视化
import matplotlib.pyplot as plt
%matplotlib inlineplt.rcParams['font.sans-serif']=['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False # 用来正常显示负号
# 创建 Erdős-Rényi 随机图,也称作 binomial graph
# n-节点数
# p-任意两个节点产生连接的概率G = nx.gnp_random_graph(100, 0.02, seed=10374196)# 初步可视化
pos = nx.spring_layout(G, seed=10)
nx.draw(G, pos)

最大连通域子图
Gcc = G.subgraph(sorted(nx.connected_components(G), key=len, reverse=True)[0])
pos = nx.spring_layout(Gcc, seed=10396953)
# nx.draw(Gcc, pos)nx.draw_networkx_nodes(Gcc, pos, node_size=20)
nx.draw_networkx_edges(Gcc, pos, alpha=0.4)
plt.figure(figsize=(12,8))
pos = nx.spring_layout(Gcc, seed=10396953)# 设置其它可视化样式
options = {"font_size": 12,"node_size": 350,"node_color": "white","edgecolors": "black","linewidths": 1, # 节点线宽"width": 2, # edge线宽
}nx.draw_networkx(Gcc, pos, **options)plt.title('Connected components of G', fontsize=20)
plt.axis('off')
plt.show()
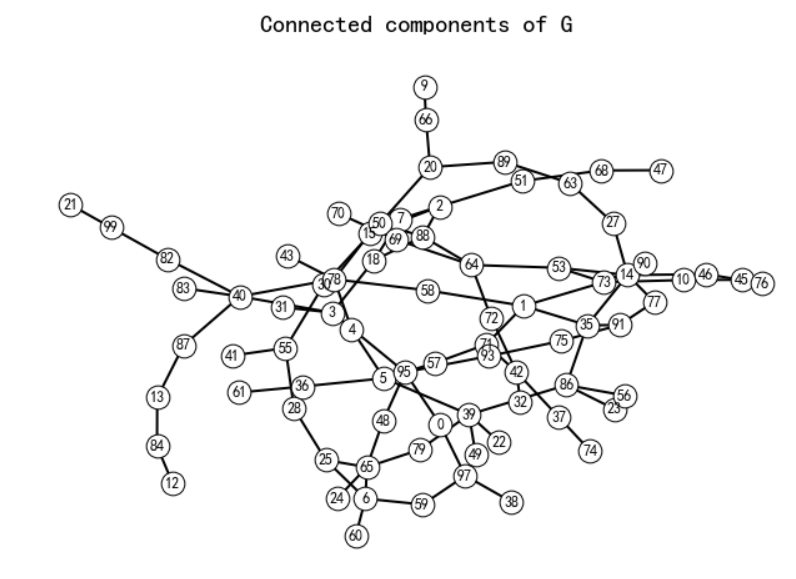
节点的连接数可视化
对节点按度的大小从大到小进行排列,绘制基本的点图
degree_sequence = sorted((d for n, d in G.degree()), reverse=True)
plt.figure(figsize=(12,8))
plt.plot(degree_sequence, "b-", marker="o")
plt.title('Degree Rank Plot', fontsize=20)
plt.ylabel('Degree', fontsize=25)
plt.xlabel('Rank', fontsize=25)
plt.tick_params(labelsize=20) # 设置坐标文字大小
plt.show()

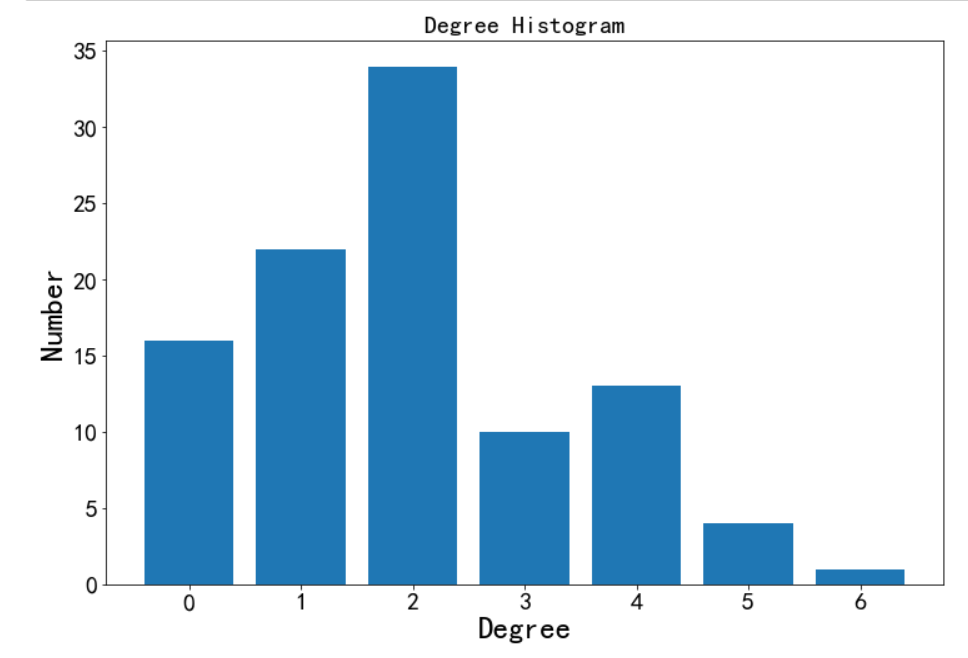
绘制直方图
X = np.unique(degree_sequence, return_counts=True)[0]
Y = np.unique(degree_sequence, return_counts=True)[1]plt.figure(figsize=(12,8))
# plt.bar(*np.unique(degree_sequence, return_counts=True))
plt.bar(X, Y)plt.title('Degree Histogram', fontsize=20)
plt.ylabel('Number', fontsize=25)
plt.xlabel('Degree', fontsize=25)
plt.tick_params(labelsize=20) # 设置坐标文字大小
plt.show()
plt.show()
棒棒糖图特征分析
# 图数据挖掘
import networkx as nx# 数据可视化
import matplotlib.pyplot as plt
%matplotlib inline# plt.rcParams['font.sans-serif']=['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False # 用来正常显示负号
导入棒棒图
# 第一个参数指定头部节点数,第二个参数指定尾部节点数
G = nx.lollipop_graph(4, 7)pos = nx.spring_layout(G, seed=3068)
nx.draw(G, pos=pos, with_labels=True)
plt.show()

图数据分析
对图的基本特征进行分析,包括:半径、直径、偏心度、中心节点、外围节点、图的密度
在图的密度中:n为节点个数,m为连接个数
对于无向图:
density=2mn(n−1)density = \frac{2m}{n(n-1)} density=n(n−1)2m
对于有向图:
density=mn(n−1)density = \frac{m}{n(n-1)} density=n(n−1)m
无连接图的density为0,全连接图的density为1,Multigraph(多重连接图)和带self
loop图的density可能大于1。
# 半径
nx.radius(G)
# 直径
nx.diameter(G)
# 偏心度:每个节点到图中其它节点的最远距离
nx.eccentricity(G)
# 中心节点,偏心度与半径相等的节点
nx.center(G)
# 外围节点,偏心度与直径相等的节点
nx.periphery(G)
# 图的密度
nx.density(G)
每两个节点之间的最短距离
pathlengths = []
for v in G.nodes():spl = nx.single_source_shortest_path_length(G, v)for p in spl:print('{} --> {} 最短距离 {}'.format(v, p, spl[p]))pathlengths.append(spl[p])
# 平均最短距离
sum(pathlengths) / len(pathlengths)
不同距离的节点对个数
dist = {}
for p in pathlengths:if p in dist:dist[p] += 1else:dist[p] = 1
计算节点特征
计算无向图和有向图的节点特征。
import networkx as nx
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
%matplotlib inline
可视化辅助函数
def draw(G, pos, measures, measure_name):nodes = nx.draw_networkx_nodes(G, pos, node_size=250, cmap=plt.cm.plasma, node_color=list(measures.values()),nodelist=measures.keys())nodes.set_norm(mcolors.SymLogNorm(linthresh=0.01, linscale=1, base=10))# labels = nx.draw_networkx_labels(G, pos)edges = nx.draw_networkx_edges(G, pos)# plt.figure(figsize=(10,8))plt.title(measure_name)plt.colorbar(nodes)plt.axis('off')plt.show()
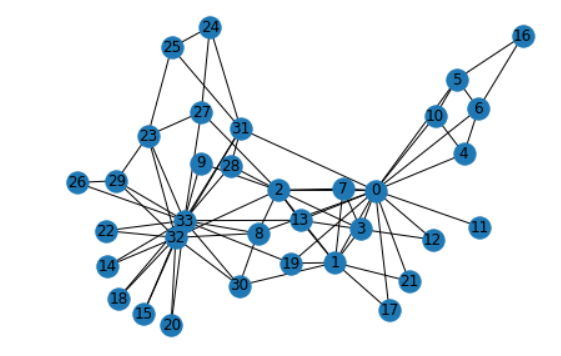
导入无向图
G = nx.karate_club_graph()
pos = nx.spring_layout(G, seed=675)
nx.draw(G, pos, with_labels=True)
导入有向图
DiG = nx.DiGraph()
DiG.add_edges_from([(2, 3), (3, 2), (4, 1), (4, 2), (5, 2), (5, 4),(5, 6), (6, 2), (6, 5), (7, 2), (7, 5), (8, 2),(8, 5), (9, 2), (9, 5), (10, 5), (11, 5)])
nx.draw(DiG, pos, with_labels=True)
Node Degree
list(nx.degree(G))dict(G.degree())
# 字典按值排序
sorted(dict(G.degree()).items(),key=lambda x : x[1], reverse=True)
draw(G, pos, dict(G.degree()), 'Node Degree')
节点重要度特征 Centrality
https://networkx.org/documentation/stable/reference/algorithms/centrality.html
Degree Centrality
无向图
nx.degree_centrality(G)draw(G, pos, nx.degree_centrality(G), 'Degree Centrality')
有向图
nx.in_degree_centrality(DiG)
nx.out_degree_centrality(DiG)draw(DiG, pos, nx.in_degree_centrality(DiG), 'DiGraph Degree Centrality')
draw(DiG, pos, nx.out_degree_centrality(DiG), 'DiGraph Degree Centrality')
Eigenvector Centrality
无向图
nx.eigenvector_centrality(G)draw(G, pos, nx.eigenvector_centrality(G), 'Eigenvector Centrality')
有向图
nx.eigenvector_centrality_numpy(DiG)draw(DiG, pos, nx.eigenvector_centrality_numpy(DiG), 'DiGraph Eigenvector Centrality')
Betweenness Centrality(必经之地)
#nx.betweenness_centrality?
#nx.betweenness_centrality??
nx.betweenness_centrality(G)draw(G, pos, nx.betweenness_centrality(G), 'Betweenness Centrality')
Closeness Centrality(去哪儿都近)
nx.closeness_centrality(G)draw(G, pos, nx.closeness_centrality(G), 'Closeness Centrality')
PageRank
nx.pagerank(DiG, alpha=0.85)draw(DiG, pos, nx.pagerank(DiG, alpha=0.85), 'DiGraph PageRank')
Katz Centrality
nx.katz_centrality(G, alpha=0.1, beta=1.0)draw(G, pos, nx.katz_centrality(G, alpha=0.1, beta=1.0), 'Katz Centrality')
draw(DiG, pos, nx.katz_centrality(DiG, alpha=0.1, beta=1.0), 'DiGraph Katz Centrality')
HITS Hubs and Authorities
h, a = nx.hits(DiG)
draw(DiG, pos, h, 'DiGraph HITS Hubs')
draw(DiG, pos, a, 'DiGraph HITS Authorities')
社群属性 Clustering
https://networkx.org/documentation/stable/reference/algorithms/clustering.html
nx.draw(G, pos, with_labels=True)
三角形个数
nx.triangles(G)draw(G, pos, nx.triangles(G), 'Triangles')
Clustering Coefficient
nx.clustering(G)
nx.clustering(G, 0)draw(G, pos, nx.clustering(G), 'Clustering Coefficient')
Bridges
如果某个连接断掉,会使连通域个数增加,则该连接是bridge。
bridge连接不属于环的一部分。
pos = nx.spring_layout(G, seed=675)
nx.draw(G, pos, with_labels=True)
list(nx.bridges(G))
[(0, 11)]
Common Neighbors 、Jaccard Coefficient和Adamic-Adar index
基于两节点局部连接信息(Local neighborhood overlap)
pos = nx.spring_layout(G, seed=675)
nx.draw(G, pos, with_labels=True)
sorted(nx.common_neighbors(G, 0, 4))
preds = nx.jaccard_coefficient(G, [(0, 1), (2, 3)])
for u, v, p in preds:print(f"({u}, {v}) -> {p:.8f}")for u, v, p in nx.adamic_adar_index(G, [(0, 1), (2, 3)]):print(f"({u}, {v}) -> {p:.8f}")
Katz Index
基于两节点在全图的连接信息(Global neighborhood overlap)
节点u到节点v,路径为k的路径个数。
import networkx as nx
import numpy as np
from numpy.linalg import inv
G = nx.karate_club_graph()# 计算主特征向量
L = nx.normalized_laplacian_matrix(G)
e = np.linalg.eigvals(L.A)
print('最大特征值', max(e))# 折减系数
beta = 1/max(e)# 创建单位矩阵
I = np.identity(len(G.nodes))# 计算 Katz Index
S = inv(I - nx.to_numpy_array(G)*beta) - I
array([[-0.630971 , 0.03760311, -0.50718655, …, 0.22028562,
0.08051109, 0.0187629 ],
[ 0.03760311, 0.0313979 , -1.09231501, …, 0.18920621,
-0.09098329, 0.08188737],
[-0.50718655, -1.09231501, 0.79993439, …, -0.4511988 ,
0.17631358, -0.23914987],
…,
[ 0.22028562, 0.18920621, -0.4511988 , …, -0.07349891,
0.47525815, -0.0457034 ],
[ 0.08051109, -0.09098329, 0.17631358, …, 0.47525815,
-0.28781332, -0.70104834],
[ 0.0187629 , 0.08188737, -0.23914987, …, -0.0457034 ,
-0.70104834, -0.50717615]])
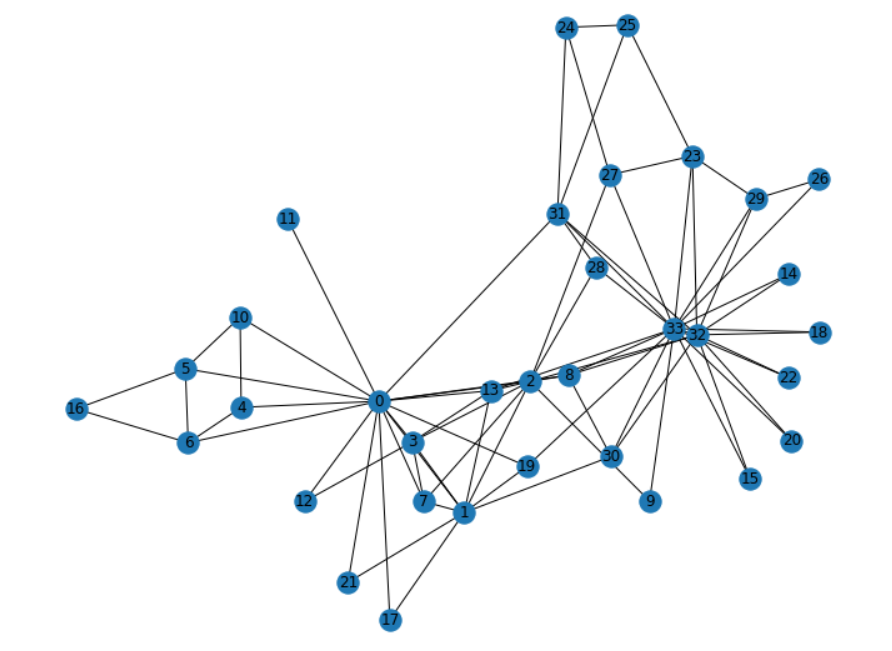
计算全图Graphlet个数
import networkx as nx
import matplotlib.pyplot as plt
%matplotlib inlineimport itertoolsG = nx.karate_club_graph()
plt.figure(figsize=(10,8))
pos = nx.spring_layout(G, seed=123)
nx.draw(G, pos, with_labels=True)
指定Graphlet
target = nx.complete_graph(3)
nx.draw(target)
匹配Graphlet,统计个数
num = 0
for sub_nodes in itertools.combinations(G.nodes(), len(target.nodes())): # 遍历全图中,符合graphlet节点个数的所有节点组合subg = G.subgraph(sub_nodes) # 从全图中抽取出子图if nx.is_connected(subg) and nx.is_isomorphic(subg, target): # 如果子图是完整连通域,并且符合graphlet特征,输出原图节点编号num += 1print(subg.edges())
num
拉普拉斯矩阵特征值分解
# 图数据挖掘
import networkx as nximport numpy as np# 数据可视化
import matplotlib.pyplot as plt
%matplotlib inlineplt.rcParams['font.sans-serif']=['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False # 用来正常显示负号import numpy.linalg # 线性代数
创建图
n = 1000 # 节点个数
m = 5000 # 连接个数
G = nx.gnm_random_graph(n, m, seed=5040)
邻接矩阵(Adjacency Matrix)
A = nx.adjacency_matrix(G)
A.todense()
matrix([[0, 0, 0, …, 0, 0, 0],
[0, 0, 0, …, 0, 0, 0],
[0, 0, 0, …, 0, 0, 0],
…,
[0, 0, 0, …, 0, 0, 0],
[0, 0, 0, …, 0, 0, 0],
[0, 0, 0, …, 0, 0, 0]], dtype=int32)
拉普拉斯矩阵(Laplacian Matrix)
L=D−AL = D - A L=D−A
L 为拉普拉斯矩阵(Laplacian Matrix)
D 为节点degree对角矩阵
A 为邻接矩阵(Adjacency Matrix)
L = nx.laplacian_matrix(G)
# 节点degree对角矩阵
D = L + A
D.todense()
matrix([[12, 0, 0, …, 0, 0, 0],
[ 0, 6, 0, …, 0, 0, 0],
[ 0, 0, 8, …, 0, 0, 0],
…,
[ 0, 0, 0, …, 8, 0, 0],
[ 0, 0, 0, …, 0, 6, 0],
[ 0, 0, 0, …, 0, 0, 7]], dtype=int64)
归一化拉普拉斯矩阵(Normalized Laplacian Matrix)
Ln=D−12LD−12L_n = D^{-\frac{1}{2}}LD^{-\frac{1}{2}} Ln=D−21LD−21
L_n = nx.normalized_laplacian_matrix(G)
L_n.todense()plt.imshow(L_n.todense())
plt.show()
特征值分解
e = np.linalg.eigvals(L_n.A)
# 最大特征值
max(e)
# 最小特征值
min(e)
特征值分布直方图
plt.figure(figsize=(12,8))plt.hist(e, bins=100)
plt.xlim(0, 2) # eigenvalues between 0 and 2plt.title('Eigenvalue Histogram', fontsize=20)
plt.ylabel('Frequency', fontsize=25)
plt.xlabel('Eigenvalue', fontsize=25)
plt.tick_params(labelsize=20) # 设置坐标文字大小
plt.show()

北京上海地铁站图数据挖掘
上海、北京地铁站点图数据挖掘,计算地铁站点的最短路径、节点重要度、集群系数、连通性。
import networkx as nx
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
%matplotlib inline
可视化辅助函数
def draw(G, pos, measures, measure_name):plt.figure(figsize=(20, 20))nodes = nx.draw_networkx_nodes(G, pos, node_size=250, cmap=plt.cm.plasma, node_color=list(measures.values()),nodelist=measures.keys())nodes.set_norm(mcolors.SymLogNorm(linthresh=0.01, linscale=1, base=10))# labels = nx.draw_networkx_labels(G, pos)edges = nx.draw_networkx_edges(G, pos)plt.title(measure_name, fontsize=30)# plt.colorbar(nodes)plt.axis('off')plt.show()
字典按值排序辅助函数
def dict_sort_by_value(dict_input):'''输入字典,输出按值排序的字典'''return sorted(dict_input.items(),key=lambda x : x[1], reverse=True)
导入地铁站连接表
数据来源:
上海地铁线路图:http://www.shmetro.com
上海地铁时刻表:http://service.shmetro.com/hcskb/index.htm
北京地铁线路图:https://map.bjsubway.com
北京地铁时刻表:https://www.bjsubway.com/station/smcsj
# 上海地铁站点连接表
df = pd.read_csv('shanghai_subway.csv')# 北京地铁站点连接表
# df = pd.read_csv('beijing_subway.csv')
df
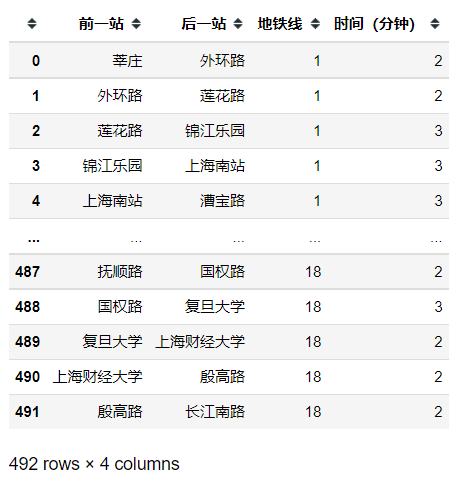
创建图
# 创建无向图
G = nx.Graph()# 从连接表创建图
for idx, row in df.iterrows(): # 遍历表格的每一行G.add_edges_from([(row['前一站'], row['后一站'])], line=row['地铁线'], time=row['时间(分钟)'])
可视化
# 节点排版布局-默认弹簧布局
pos = nx.spring_layout(G, seed=123)# 节点排版布局-每个节点单独设置坐标
# pos = {1: [0.1, 0.9], 2: [0.4, 0.8], 3: [0.8, 0.9], 4: [0.15, 0.55],
# 5: [0.5, 0.5], 6: [0.8, 0.5], 7: [0.22, 0.3], 8: [0.30, 0.27],
# 9: [0.38, 0.24], 10: [0.7, 0.3], 11: [0.75, 0.35]}
plt.figure(figsize=(15,15))
nx.draw(G, pos=pos)
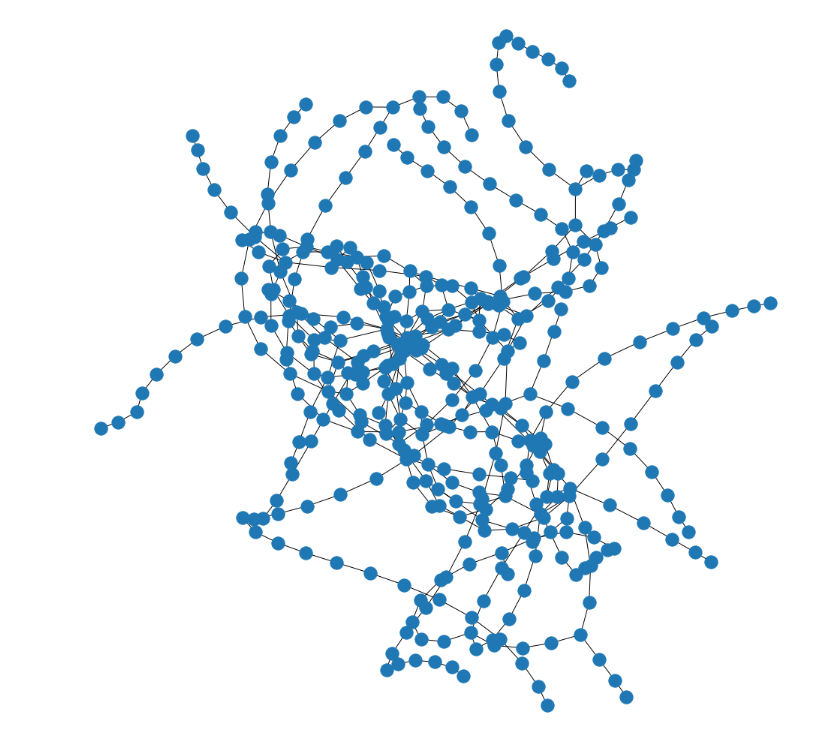
Shortest Path 最短路径
NetworkX-最短路径算法:https://networkx.org/documentation/stable/reference/algorithms/shortest_paths.html
# 任意两节点之间是否存在路径
nx.has_path(G, source='昌吉东路', target='同济大学')# 任意两节点之间的最短路径
nx.shortest_path(G, source='昌吉东路', target='同济大学', weight='time')# 任意两节点之间的最短路径长度
nx.shortest_path_length(G, source='昌吉东路', target='同济大学', weight='time')# 全图平均最短路径
nx.average_shortest_path_length(G, weight='time')# 某一站去其他站的最短路径
nx.single_source_shortest_path(G, source='同济大学')#某一站去其他站的最短路径长度
nx.single_source_shortest_path_length(G, source='同济大学')
地图导航系统
# 指定起始站和终点站
A_station = '昌吉东路'
B_station = '同济大学'# 获取最短路径
shortest_path_list = nx.shortest_path(G, source=A_station, target=B_station, weight='time')for i in range(len(shortest_path_list)-1):previous_station = shortest_path_list[i]next_station = shortest_path_list[i+1]line_id = G.edges[(previous_station, next_station)]['line'] # 地铁线编号time = G.edges[(previous_station, next_station)]['time'] # 时间print('{}--->{} {}号线 {}分钟'.format(previous_station, next_station, line_id, time)) # 输出结果# 最短路径长度
print('共计 {} 分钟'.format(nx.shortest_path_length(G, source=A_station, target=B_station, weight='time')))
昌吉东路—>上海赛车场 11号线 4分钟
上海赛车场—>嘉定新城 11号线 4分钟
嘉定新城—>马陆 11号线 3分钟
马陆—>陈翔公路 11号线 4分钟
陈翔公路—>南翔 11号线 3分钟
南翔—>桃浦新村 11号线 3分钟
桃浦新村—>武威路 11号线 3分钟
武威路—>祁连山路 11号线 2分钟
祁连山路—>李子园 11号线 3分钟
李子园—>上海西站 11号线 2分钟
上海西站—>真如 11号线 3分钟
真如—>枫桥路 11号线 2分钟
枫桥路—>曹杨路 11号线 2分钟
曹杨路—>镇坪路 4号线 3分钟
镇坪路—>中潭路 4号线 2分钟
中潭路—>上海火车站 4号线 3分钟
上海火车站—>宝山路 4号线 4分钟
宝山路—>海伦路 4号线 3分钟
海伦路—>邮电新村 10号线 2分钟
邮电新村—>四平路 10号线 2分钟
四平路—>同济大学 10号线 2分钟
共计 59 分钟
PageRank
draw(G, pos, nx.pagerank(G, alpha=0.85), 'PageRank')
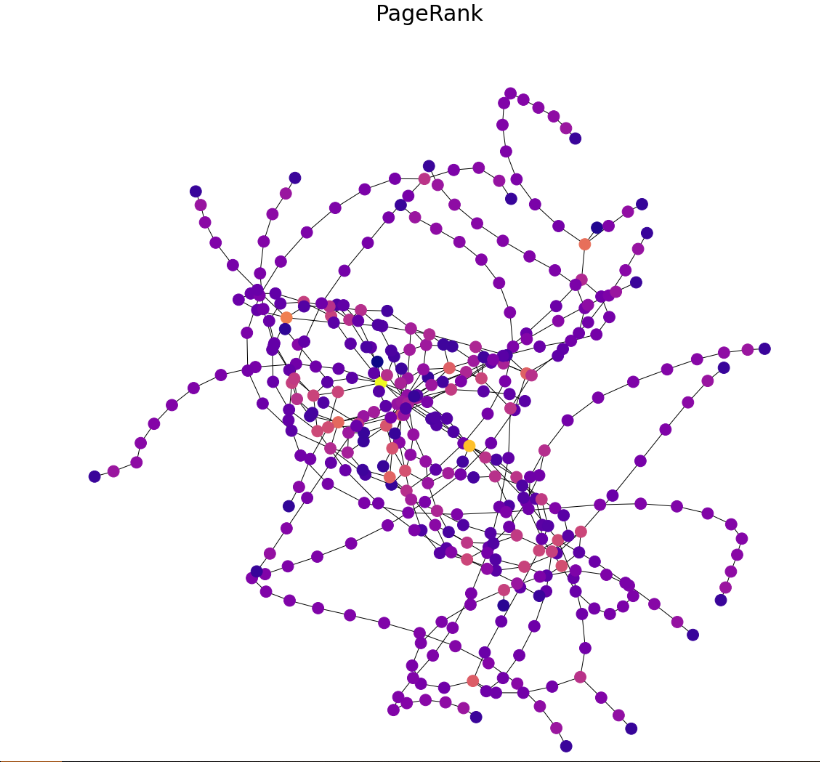
同样我们也可以计算节点的其它特征
总结
本篇文章主要介绍了NetworkX工具包实战在特征工程上的使用,利用NetworkX工具包对节点的度、节点重要度特征 、社群属性和等算法和拉普拉斯矩阵特征值分解等进行了计算,最后对北京上海地铁站图数据进行了挖掘。
相关文章:

三、NetworkX工具包实战3——特征工程【CS224W】(Datawhale组队学习)
开源内容:https://github.com/TommyZihao/zihao_course/tree/main/CS224W 子豪兄B 站视频:https://space.bilibili.com/1900783/channel/collectiondetail?sid915098 斯坦福官方课程主页:https://web.stanford.edu/class/cs224w NetworkX…...

分布式之Raft共识算法分析
写在前面 在分布式之Paxos共识算法分析 一文中我们分析了paxos算法,知道了其包括basic paxos和multi paxos,并了解了multi paxos只是一种分布式共识算法的思想,而非具体算法,但可根据其设计具体的算法,本文就一起来看…...

数据库——范式
目录 一、概念 二、各范式 第一范式 第二范式 第三范式 BC范式 第四范式 第五范式(略) 一、概念 基本概念 关系:通常一个关系对应一张表;元组:一行;属性:一列;码࿱…...
:Geospatial Data in Python)
Geospatial Data Science(2):Geospatial Data in Python
Geospatial Data Science(2):Geospatial Data in Python PART 1: 检查数据 1.1 Imports import geopandas as gpd # for geospatial data handling import osmnx # for handling data from OpenStreetMap (osm) with the help of networkX (nx) import contextily as cx # f…...
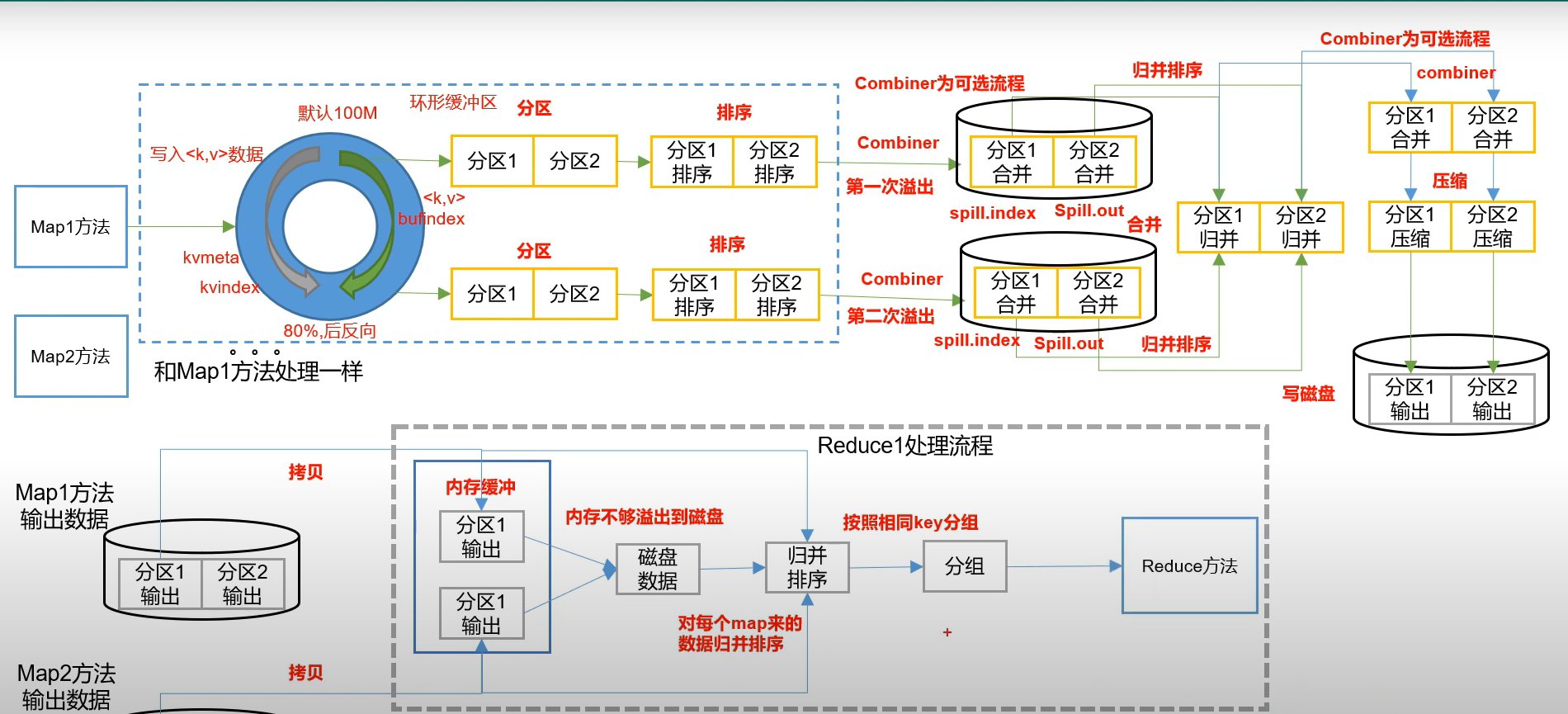
16.hadoop系列之MapReduce之MapTask与ReduceTask及Shuffle工作机制
1.MapTask工作机制 以上内容我们之前文章或多或少介绍过,就已网络上比较流行的该图进行理解学习吧 MapTask分为五大阶段 Read阶段Map阶段Collect阶段溢写阶段Merge阶段 2.ReduceTask工作机制 ReduceTask分为三大阶段 Copy阶段Sort阶段Reduce阶段 3.ReduceTask并…...

java 面试过程中遇到的几个问题记录20230220
微服务注册中心的作用微服务注册中心的作用是协调和管理微服务实例的注册和发现。它充当了服务注册表,可以维护服务实例的元数据,例如服务名称、IP 地址和端口号等。当一个微服务启动时,它会向注册中心注册自己的元数据,以使其他服…...

面试题:【数据库三】索引简述
目录 一、索引是什么 二、索引规则 三、索引失效场景 一、索引是什么 索引是帮助Mysql高效获取数据的【数据结构】索引存储在文件系统中索引的文件存储形式与存储引擎相关 mysql有三种存储引擎 InnoDBMyISAMMEMORY索引文件的结构 Hash Hash索引底层是哈希表,哈希…...
数据库必知必会:TiDB(12)TiDB连接管理
数据库必知必会:TiDB(12)TiDB连接管理TiDB连接管理TiDB的连接特性连接TiDBMySQL命令行客户端图形界面客户端连接其他连接方式写在后面TiDB连接管理 TiDB的连接特性 TiDB Server主要负责接收用户的会话请求,接收SQL并负责SQL语句…...
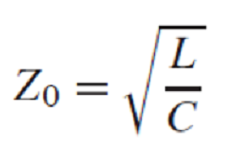
电源大事,阻抗二字
作者:一博科技高速先生成员 姜杰PCB设计时,我们通常会控制走线的特征阻抗;电源设计时,又会关注电源分配系统(PDN)的交流阻抗,虽然都是阻抗,一个是信号的通道要求,一个是电…...

ASE20N60-ASEMI的MOS管ASE20N60
编辑-Z ASE20N60在TO-247封装里的静态漏极源导通电阻(RDS(ON))为0.4Ω,是一款N沟道高压MOS管。ASE20N60的最大脉冲正向电流ISM为80A,零栅极电压漏极电流(IDSS)为10uA,其工作时耐温度范围为-55~150摄氏度。ASE20N60功耗…...
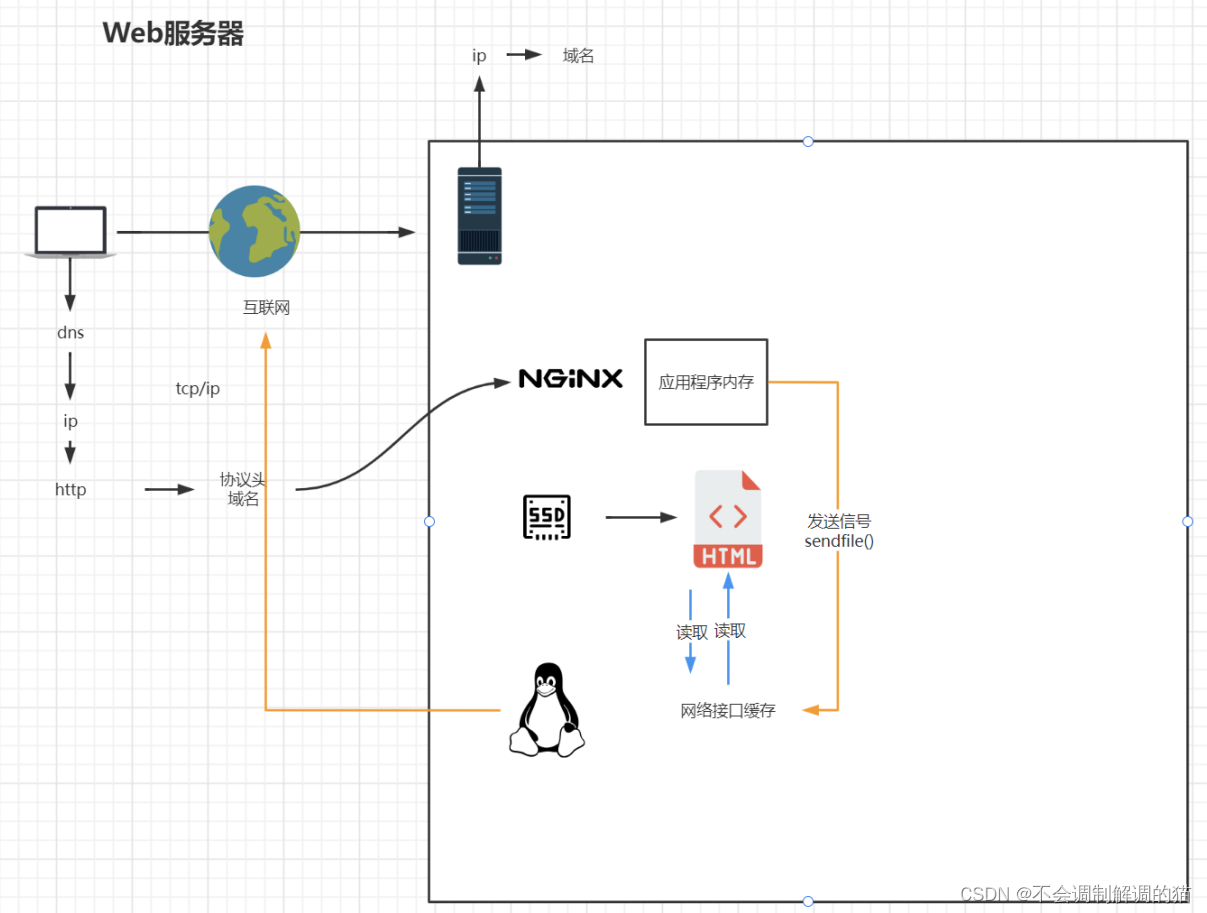
nginx 代理01(持续更新)
1、如果请求是post,而且请求原是188.188.3.171,处理方式403 if ($request_method ~* "POST") # $request_method 等同于request的method,通常是“GET”或“POST” # 如果访问request的method值为POST则返回“o” {set…...
初阶C语言——操作符【详解】
文章目录1.算术操作符2.移位操作符2.1 左移操作符2.2 右移操作符3.位操作符按位与按位或按位异或4.赋值操作符复合赋值符5.单目操作符5.1单目操作符介绍6.关系操作符7.逻辑操作符8.条件操作符9.逗号表达式10.下标引用、函数调用和结构成员11表达式求值11.1 隐式类型转换11.2算术…...

37k*16 薪,年后直接上岗,3年自动化测试历经3轮面试成功拿下阿里Offer....
前言 转眼过去,距离读书的时候已经这么久了吗?,从18年5月本科毕业入职了一家小公司,到现在快4年了,前段时间社招想着找一个新的工作,前前后后花了一个多月的时间复习以及面试,前几天拿到了阿里…...
利用Rust与Flutter开发一款小工具
1.起因 起因是年前看到了一篇Rust iOS & Android|未入门也能用来造轮子?的文章,作者使用Rust做了个实时查看埋点的工具。其中作者的一段话给了我启发: 无论是 LookinServer 、 Flipper 等 Debug 利器,还是 Flutt…...

零入门kubernetes网络实战-16->使用golang给docker环境下某个容器里添加一个额外的网卡
《零入门kubernetes网络实战》视频专栏地址 https://www.ixigua.com/7193641905282875942 本篇文章视频地址(稍后上传) 上一篇文章,我们使用了golang在veth pair链接的网络命名空间里添加了网卡, 本篇文章,我尝试,在docker环境下…...
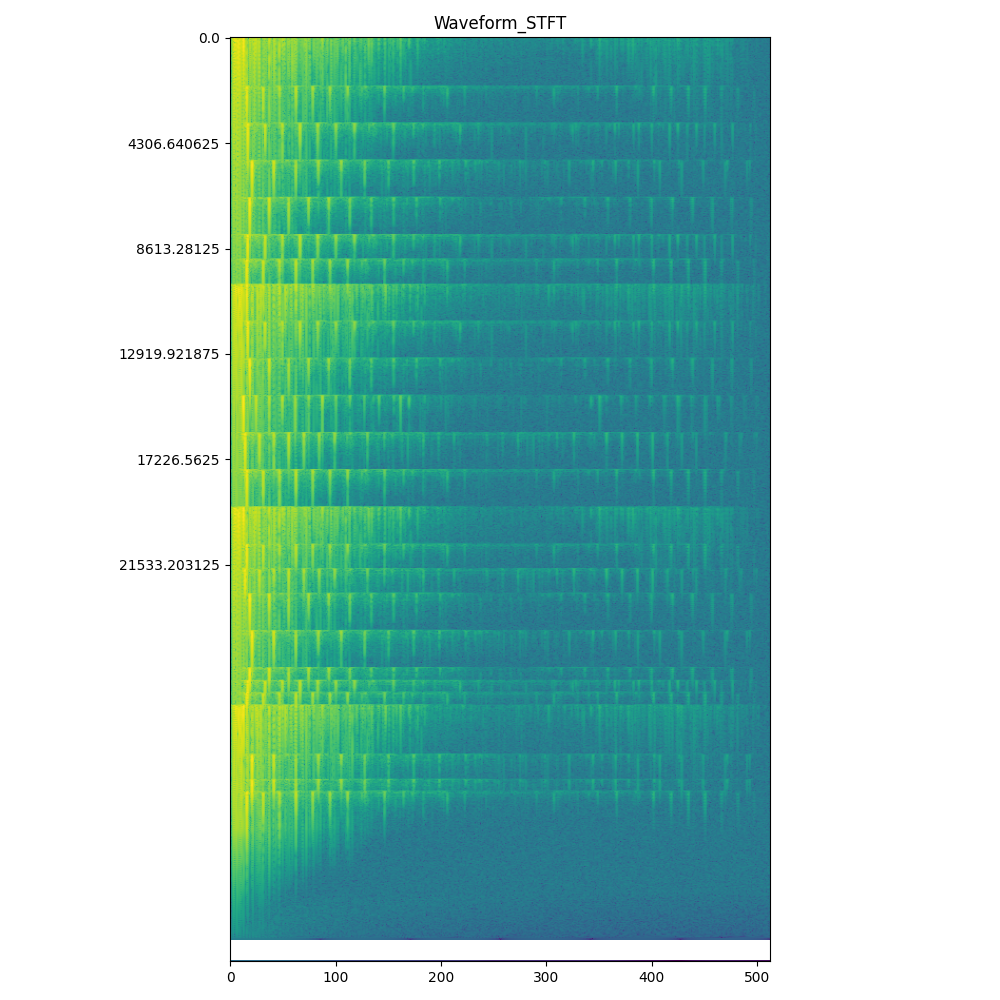
音频信号处理笔记(二)
文章目录1.1.3 过零率1.1.4 谱质心和子带带宽1.1.5 短时傅里叶分析法1.1.6 小波变换相关课程: 音频信号处理及深度学习教程傅里叶分析之掐死教程(完整版)更新于2014.06.06 - 知乎 (zhihu.com)1.1.3 过零率 过零率:是一个信号符号…...

钓鱼网站+bypassuac提权
本实验实现1 :要生成一个钓鱼网址链接,诱导用户点击,实验过程是让win7去点击这个钓鱼网站链接,则会自动打开一个文件共享服务器的文件夹,在这个文件夹里面会有两个文件,当用户分别点击执行后,则…...
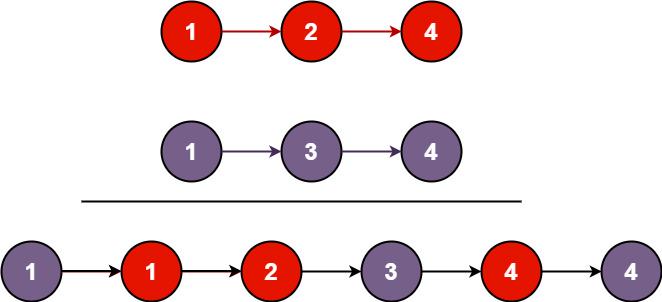
合并两个有序链表——递归解法
题目描述21. 合并两个有序链表难度简单2922收藏分享切换为英文接收动态反馈将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 示例 1:输入:l1 [1,2,4], l2 [1,3,4]输出:[1,1,2,3,4,4]示例…...
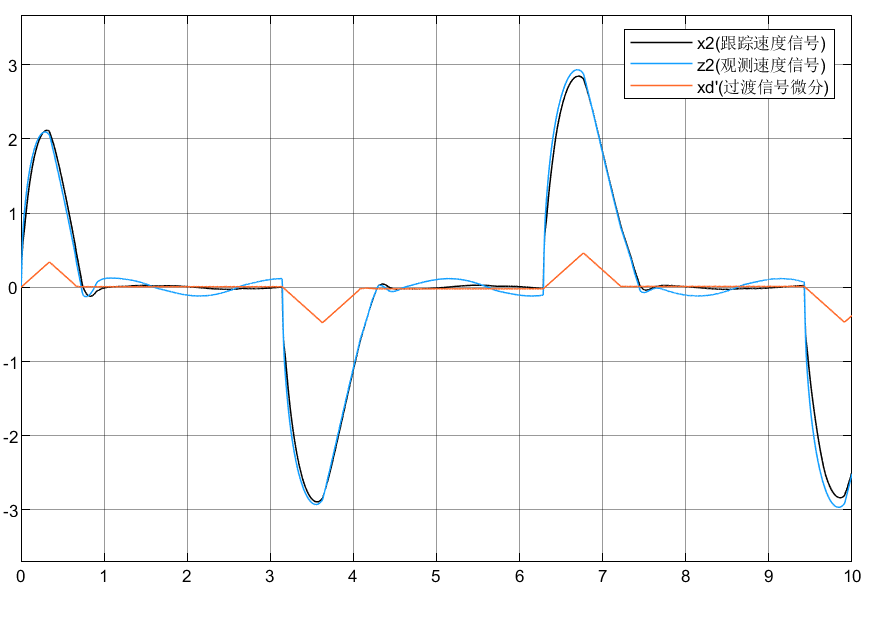
ADRC自抗扰控制总结
目录 前言 1.ADRC形式 1.1形一 1.2形二 2.被控对象 3.仿真分析 3.1仿真模型 3.2仿真结果 4.学习问题 前言 前面的3篇文章依次介绍了微分跟踪器TD、状态观测器ESO和非线性状态误差反馈NLSEF三部分内容,至此ADRC的结构已经介绍完毕,现在对分块学习…...
3年工作之后是不是还在“点点点”,3年感悟和你分享....
经常都有人问我软件测试前景怎么样,每年也都帮助很多朋友做职业分析和学习规划,也很欣慰能够通过自己的努力帮到一些人进入到大厂。 2023年软件测试行业的发展现状以及未来的前景趋势 最近很多测试人在找工作的时候,明显的会发现功能测试很…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...