【多思路解决喝汽水问题】1瓶汽水1元,2个空瓶可以换一瓶汽水,给20元,可以喝多少汽水
题目内容
喝汽水问题
喝汽水,1瓶汽水1元,2个空瓶可以换一瓶汽水,给20元,可以喝多少汽水(编程实现)。
题目分析
数学思路分析
根据给出的问题和引用内容,我们可以得出答案。
首先,我们用20元购买了20瓶汽水,现在有20个空瓶。
接下来,我们将这20个空瓶兑换成新的10瓶汽水。
然后,将这10个空瓶再次兑换成新的5瓶汽水,此时还剩下一个空瓶。
我们将这个剩余的空瓶与后面的空瓶结合兑换,得到1瓶新的汽水。
因此,到目前为止,我们总共获得了20+10+5+2+1+1=39瓶汽水。
所以,给了20元我们可以喝到39瓶汽水。
编程思路分析
思路一 循环实现
total = 20; //汽水总数
int k = 0; //空瓶数
int s = 0 ; //剩余空瓶
第一次(k=20)。
第二次(k=20/2=10,s=20%2=0),此时total又增加10了;
第三次(k=10/2=5,s=10%2=0);
第四次(k=5/2=2, s=5%2=1,);
第五次(k=2/2=1,s=2%2=0);
(s=1)。
#include<stdio.h>
#include<stdlib.h>
int main()
{int total = 20; //汽水总数int k = 0; //空瓶数int s = 0 ; //剩余空瓶k = 20;while(k>=1){k= k+s;total = total+k/2;//原有的汽水数+换来的汽水数s = k%2;k=k/2;//两个空瓶子换1个新汽水,汽水喝完就是1个瓶子}printf("%d\n",total);system("pause");return 0;
}
思路二 递归实现
第一次和第二次买汽水 ,分别花了一块钱(+2),
从第三次开始,每次去花一块钱买汽水,再加上用第一次和第二次的空瓶子可以换来一瓶,一共可以获得两瓶汽水(+2),
第四次拿着第三次那两空瓶子,再花一块钱,又可以得到两瓶汽水(+2),
第五次,第六次,以此类推,接下来的每一次都是相当于花1元钱和两个空瓶子,来获得两瓶新的汽水。
那么到最后一次时,手里已经没有钱了,即此时只有两个空瓶子换来一瓶汽水(+1)。
把去买汽水的过程定义为一个函数就可以递归计算最终结果。
#include<stdio.h>
#include<stdlib.h>
int Buy(int money)
{if(money==1)return 1;else return Buy(money-1)+2;
}
int main()
{int money = 20;printf("%d\n",Buy(money));system("pause");return 0;
}
相关文章:

【多思路解决喝汽水问题】1瓶汽水1元,2个空瓶可以换一瓶汽水,给20元,可以喝多少汽水
题目内容 喝汽水问题 喝汽水,1瓶汽水1元,2个空瓶可以换一瓶汽水,给20元,可以喝多少汽水(编程实现)。 题目分析 数学思路分析 根据给出的问题和引用内容,我们可以得出答案。 首先ÿ…...
)
P1591 阶乘数码(Java高精度)
题目描述 求 n ! n! n! 中某个数码出现的次数。 输入格式 第一行为 t ( t ≤ 10 ) t(t \leq 10) t(t≤10),表示数据组数。接下来 t t t 行,每行一个正整数 n ( n ≤ 1000 ) n(n \leq 1000) n(n≤1000) 和数码 a a a。 输出格式 对于每组数据&a…...

Mybatis的动态SQL及关键属性和标识的区别(对SQL更灵活的使用)
( 虽然文章中有大多文本内容,想了解更深需要耐心看完,必定大有受益 ) 目录 一、动态SQL ( 1 ) 是什么 ( 2 ) 作用 ( 3 ) 优点 ( 4 ) 特殊标签 ( 5 ) 演示 二、#和$的区别 2.1 #使用 ( 1 ) #占位符语法 ( 2 ) #优点 2.…...
mysql下载
网址 MySQL :: Download MySQL Community Serverhttps://dev.mysql.com/downloads/mysql/ 2、选择MSI进行安装 3、这里我选择离线安装 4、这里我选择直接下载 5、等待下载安装即可...

聚合函数与窗口函数
聚合函数 回答一 聚合函数(Aggregate Functions)是SQL中的函数,用于对一组数据进行计算,并返回单个结果。聚合函数通常用于统计和汇总数据,包括计算总和、平均值、计数、最大值和最小值等。 以下是一些常见的聚合函…...
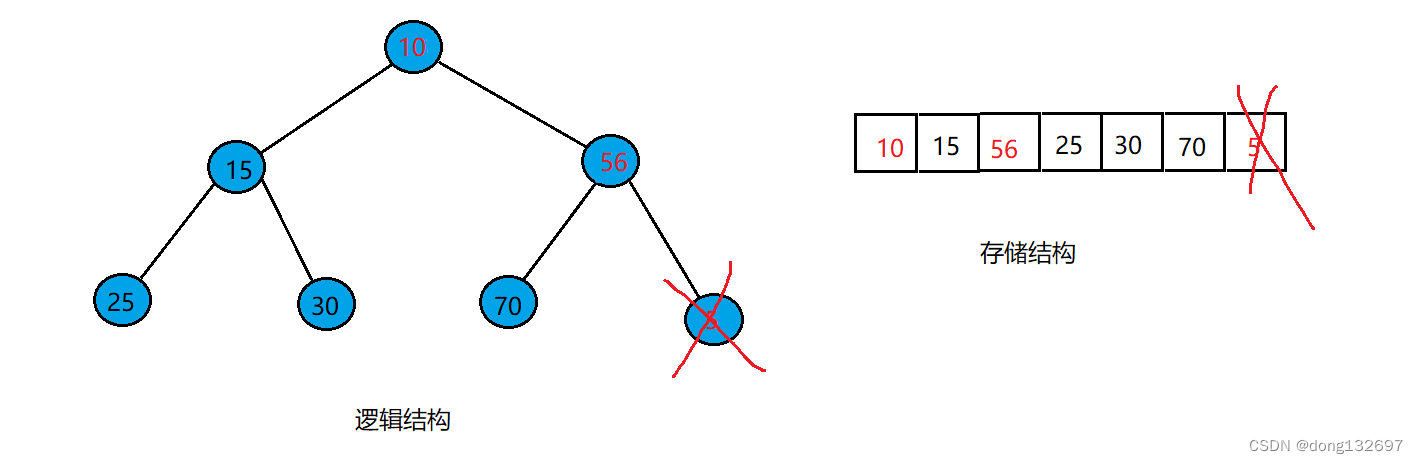
c语言实现堆
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、树1、树的概念2、树的相关概念3、树的表示 二、二叉树1、二叉树概念2、特殊的二叉树3、二叉树的性质4、二叉树的顺序结构5、二叉树的链式结构 三、堆(二叉树…...

ubuntu 如何将文件打包成tar.gz
要将文件打包成.tar.gz文件,可以使用以下命令: tar -czvf 文件名.tar.gz 文件路径 其中,-c表示创建新的归档文件,-z表示使用gzip进行压缩,-v表示显示详细的打包过程,-f表示指定归档文件的名称。 例如&am…...
)
前端优化页面加载速度的方法(持续更新)
提速方法方向 延迟脚本加载 使用 async 属性: 在这种方法中,脚本将在下载完成后立即执行,而不会阻塞其他页面资源的加载和渲染。这适用于那些不依赖于其他脚本和页面内容的脚本,例如分析脚本等。示例如下: html …...

利用SSL证书的SNI特性建立自己的爬虫ip服务器
今天我要和大家分享一个关于自建多域名HTTPS爬虫ip服务器的知识,让你的爬虫ip服务器更加强大!无论是用于数据抓取、反爬虫还是网络调试,自建一个支持多个域名的HTTPS爬虫ip服务器都是非常有价值的。本文将详细介绍如何利用SSL证书的SNI&#…...

HTML和CSS
HTML HTML(Hyper Text Markup Language):超文本语言 超文本:超越了文本的限制,比普通文本更强大。除了文字信息,还可以定义图片、音频、视频等内容。 标记语言:由标签构成的语言 HTML标签都是预定义好的。例如:使用&l…...

C#的IndexOf
在 C# 中,IndexOf 是一个字符串、数组或列表的方法,用于查找指定元素的第一个匹配项的索引。它返回一个整数值,表示匹配项在集合中的位置,如果未找到匹配项,则返回 -1。 IndexOf 方法有多个重载形式,可以根…...

深度学习2.神经网络、机器学习、人工智能
目录 深度学习、神经网络、机器学习、人工智能的关系 大白话解释深度学习 传统机器学习 VS 深度学习 深度学习的优缺点 4种典型的深度学习算法 卷积神经网络 – CNN 循环神经网络 – RNN 生成对抗网络 – GANs 深度强化学习 – RL 总结 深度学习 深度学习、神经网络…...

利用LLM模型微调的短课程;钉钉宣布开放智能化底座能力
🦉 AI新闻 🚀 钉钉宣布开放智能化底座能力AI PaaS,推动企业数智化转型发展 摘要:钉钉在生态大会上宣布开放智能化底座能力AI PaaS,与生态伙伴探寻企业服务的新发展道路。AI PaaS结合5G、云计算和人工智能技术的普及和…...
 UML之用例图详解)
软件工程(七) UML之用例图详解
1、UML-4+1视图 UML-4+1视图将会与后面的架构4+1视图会一一对应上 视图往往出现在什么场景:我们看待一个事物,我们觉得它很复杂,难以搞清楚,为了化繁为简,我们会从一个侧面去看,这就是视图。而4+1视图就是分不同角度去看事物。 逻辑视图(logical view) 一般使用类与对…...
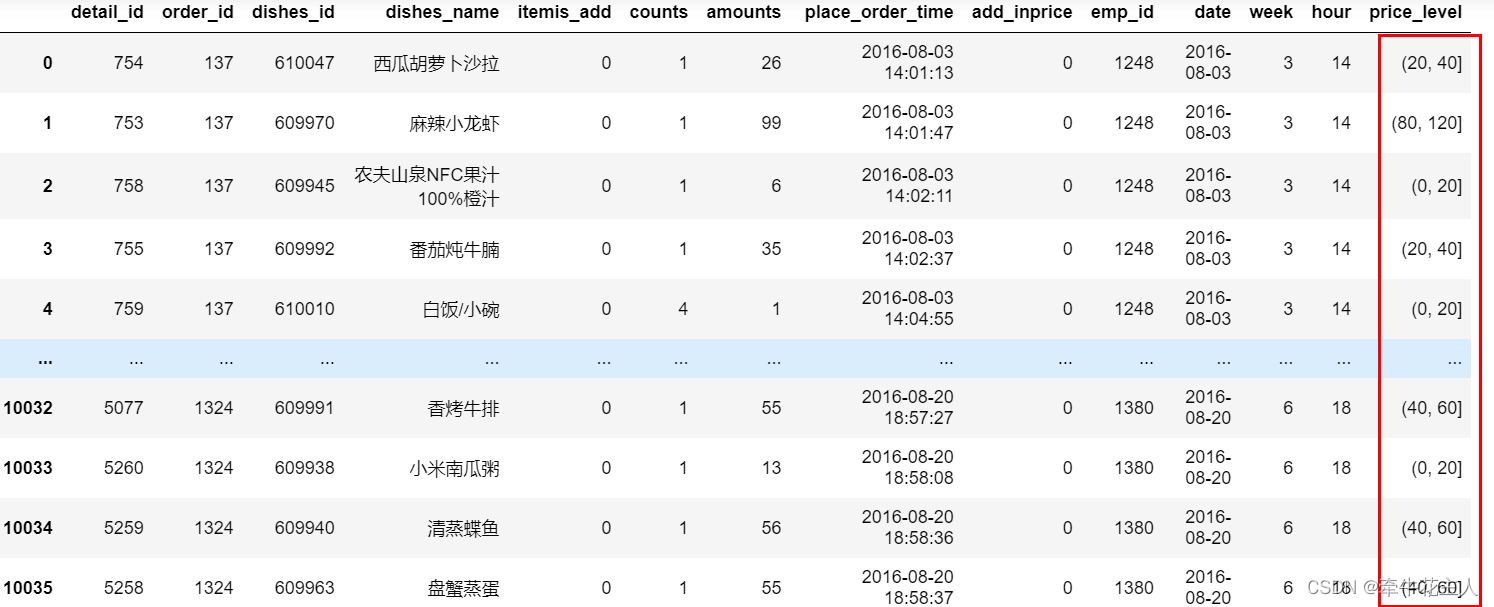
pd.cut()函数--Pandas
1. 函数功能 将连续性数值进行离散化处理:如对年龄、消费金额等进行分组 2. 函数语法 pandas.cut(x, bins, rightTrue, labelsNone, retbinsFalse, precision3, include_lowestFalse, duplicatesraise, orderedTrue)3. 函数参数 参数含义x要离散分箱操作的数组&…...

DataBinding的基本使用
目录 一、MVC、MVP和MVVM框架的使用场景二、Java使用 一、MVC、MVP和MVVM框架的使用场景 MVC: 适用于小型项目,够灵活, 缺点:Activity不仅要做View的事情还要做控制和模型的处理,导致Activity太过臃肿,管理…...
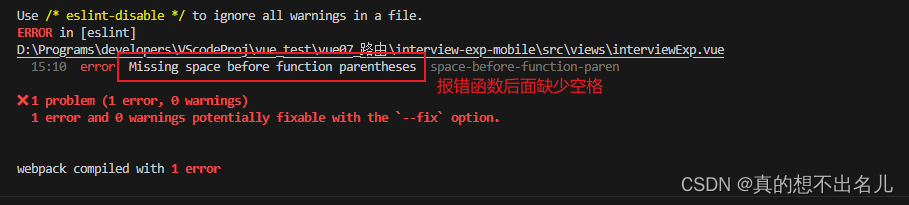
eslint和prettier格式化冲突
下载插件 ESLint 和 Prettier ESLint 进入setting.json中 setting.json中配置 {"editor.tabSize": 2,"editor.linkedEditing": true,"security.workspace.trust.untrustedFiles": "open","git.autofetch": true,"…...
matlab使用教程(26)—常微分方程的求解
1.求解非刚性 ODE 本页包含两个使用 ode45 来求解非刚性常微分方程的示例。MATLAB 提供几个非刚性 ODE 求解器。 • ode45 • ode23 • ode78 • ode89 • ode113 对于大多数非刚性问题,ode45 的性能最佳。但对于允许较宽松的误差容限或刚度适中的问题&…...

尚硅谷宋红康MySQL笔记 14-18
是记录,不会太详细,受本人知识限制会有错误,会有个人的理解在里面 第14章 视图 了解一下,数据库的常见对象 对象描述表(TABLE)表是存储数据的逻辑单元,以行和列的形式存在,列就是字段,行就是记…...
香港全新的虚拟资产服务商发牌制度
香港证监会2023年2月20日通告,原有虛擬資產交易平台如要符合資格參與當作為獲發牌的安排,必須在2023 年6 月1 日至2024 年2 月29 日期間(即由2023 年6 月1 日37起計九個月內)內,根據《打擊洗錢條例》下的虛擬資產服務提供者制度在網上提交完全…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...
