PRML笔记2-关于回归参数w的先验的理解
接上篇,现在考虑给w\boldsymbol{w}w加入先验,考虑最简单的假设,也就是w\boldsymbol{w}w服从均值为0,协方差矩阵为α−1I\alpha^{-1}\boldsymbol{I}α−1I的高斯分布。
p(w∣α)=N(w∣0,α−1I)=(α2π)(M+1)/2exp{−α2wTw}\begin{aligned} p(\boldsymbol{w}|\alpha)&=\mathcal{N}(\boldsymbol{w}|0,\alpha^{-1}\boldsymbol{I})\\ &=(\frac{\alpha}{2\pi})^{(M+1)/2}\exp\{-\frac{\alpha}{2}\boldsymbol{w}^T\boldsymbol{w}\} \end{aligned} p(w∣α)=N(w∣0,α−1I)=(2πα)(M+1)/2exp{−2αwTw}我们一步一步看一下给定(x,t,α,β)(\boldsymbol{x},\boldsymbol{t},\alpha,\beta)(x,t,α,β)后,参数w\boldsymbol{w}w的概率
p(w∣t)=p(t∣w)p(w)p(t)p(w∣t,x,α,β)=p(t∣w,x,α,β)p(w∣x,α,β)p(t∣x,α,β)\begin{aligned} p(\boldsymbol{w}|\boldsymbol{t})&=\frac{p(\boldsymbol{t}|\boldsymbol{w})p(\boldsymbol{w})}{p(\boldsymbol{t})}\\ p(\boldsymbol{w}|\boldsymbol{t},\boldsymbol{x},\alpha,\beta)&=\frac{p(\boldsymbol{t}|\boldsymbol{w},\boldsymbol{x},\alpha,\beta)p(\boldsymbol{w}|\boldsymbol{x},\alpha,\beta)}{p(\boldsymbol{t}|\boldsymbol{x},\alpha,\beta)} \end{aligned} p(w∣t)p(w∣t,x,α,β)=p(t)p(t∣w)p(w)=p(t∣x,α,β)p(t∣w,x,α,β)p(w∣x,α,β)
由于α\alphaα和ttt独立,因此上式似然函数p(t∣w,x,α,β)=p(t∣w,x,β)p(\boldsymbol{t}|\boldsymbol{w},\boldsymbol{x},\alpha,\beta)=p(\boldsymbol{t}|\boldsymbol{w},\boldsymbol{x},\beta)p(t∣w,x,α,β)=p(t∣w,x,β),而w\boldsymbol{w}w的先验我们已经有了假设,因此得到书上的结果(此处个人理解):
p(w∣x,t,α,β)∝p(t∣x,w,β)p(w∣α)p(\boldsymbol{w}|\boldsymbol{x},\boldsymbol{t},\alpha,\beta)\propto p(\boldsymbol{t}|\boldsymbol{x},\boldsymbol{w},\beta)p(\boldsymbol{w}|\alpha) p(w∣x,t,α,β)∝p(t∣x,w,β)p(w∣α)
现在成了,我们最大化后验概率求w\boldsymbol{w}w,变成了最大化似然函数p(t∣x,w,β)p(\boldsymbol{t}|\boldsymbol{x},\boldsymbol{w},\beta)p(t∣x,w,β)和先验概率p(w∣α)p(\boldsymbol{w}|\alpha)p(w∣α)乘积的值。由于p(t∣x,w,β)=∏n=1NN(tn∣y(xn,w),β−1)=∏n=1N1(2π)12β−12exp(tn−y(xn,w))2−2β−1p(\boldsymbol{t}|\boldsymbol{x},\boldsymbol{w},\beta)=\prod_{n=1}^N\mathcal{N}(t_n|y(x_n,\boldsymbol{w}),\beta^{-1})=\prod_{n=1}^N\frac{1}{(2\pi)^{\frac{1}{2}}\beta^{-\frac{1}{2}}}exp{\frac{(t_n-y(x_n,\boldsymbol{w}))^2}{-2\beta^{-1}}}p(t∣x,w,β)=n=1∏NN(tn∣y(xn,w),β−1)=n=1∏N(2π)21β−211exp−2β−1(tn−y(xn,w))2
p(w∣α)=N(w∣0,α−1I)=(α2π)(M+1)/2exp{−α2wTw}\begin{aligned} p(\boldsymbol{w}|\alpha)&=\mathcal{N}(\boldsymbol{w}|0,\alpha^{-1}\boldsymbol{I})\\ &=(\frac{\alpha}{2\pi})^{(M+1)/2}\exp\{-\frac{\alpha}{2}\boldsymbol{w}^T\boldsymbol{w}\} \end{aligned} p(w∣α)=N(w∣0,α−1I)=(2πα)(M+1)/2exp{−2αwTw}
因此
p(t∣x,w,β)p(w∣α)=[∏n=1N1(2π)12β−12exp(tn−y(xn,w))2−2β−1](α2π)(M+1)/2exp{−α2wTw}\begin{aligned} p(\boldsymbol{t}|\boldsymbol{x},\boldsymbol{w},\beta)p(\boldsymbol{w}|\alpha)& =\left[\prod_{n=1}^N\frac{1}{(2\pi)^{\frac{1}{2}}\beta^{-\frac{1}{2}}}exp{\frac{(t_n-y(x_n,\boldsymbol{w}))^2}{-2\beta^{-1}}}\right] \left(\frac{\alpha}{2\pi}\right)^{(M+1)/2}\exp\{-\frac{\alpha}{2}\boldsymbol{w}^T\boldsymbol{w}\} \end{aligned} p(t∣x,w,β)p(w∣α)=[n=1∏N(2π)21β−211exp−2β−1(tn−y(xn,w))2](2πα)(M+1)/2exp{−2αwTw}两边取ln可得
lnp(t∣x,w,β)p(w∣α)=−β2∑n=1N{y(xn,w)−tn}2+N2lnβ−N2ln(2π)+M+12lnα−M+12ln2π−α2wTw\begin{aligned} \ln{p}(\boldsymbol{t}|\boldsymbol{x},\boldsymbol{w},\beta)p(\boldsymbol{w}|\alpha) &=-\frac{\beta}{2}\sum_{n=1}^N\{y(x_n,\boldsymbol{w})-t_n\}^2+\frac{N}{2}\ln{\beta}-\frac{N}{2}\ln{(2\pi)} +\frac{M+1}{2}\ln{\alpha}-\frac{M+1}{2}\ln{2\pi}-\frac{\alpha}{2}\boldsymbol{w}^T\boldsymbol{w} \end{aligned} lnp(t∣x,w,β)p(w∣α)=−2βn=1∑N{y(xn,w)−tn}2+2Nlnβ−2Nln(2π)+2M+1lnα−2M+1ln2π−2αwTw我们现在要找的是最可能的w\boldsymbol{w}w的值,因此只考虑与w\boldsymbol{w}w有关的部门,去掉常数可得:
lnp(t∣x,w,β)p(w∣α)=−β2∑n=1N{y(xn,w)−tn}2−α2wTw\begin{aligned} \ln{p}(\boldsymbol{t}|\boldsymbol{x},\boldsymbol{w},\beta)p(\boldsymbol{w}|\alpha)&=-\frac{\beta}{2}\sum_{n=1}^N\{y(x_n,\boldsymbol{w})-t_n\}^2-\frac{\alpha}{2}\boldsymbol{w}^T\boldsymbol{w} \end{aligned} lnp(t∣x,w,β)p(w∣α)=−2βn=1∑N{y(xn,w)−tn}2−2αwTw这就相当于最小化
β2∑n=1N{y(xn,w)−tn}2+α2wTw\frac{\beta}{2}\sum_{n=1}^N\{y(x_n,\boldsymbol{w})-t_n\}^2+\frac{\alpha}{2}\boldsymbol{w}^T\boldsymbol{w} 2βn=1∑N{y(xn,w)−tn}2+2αwTw
相关文章:

PRML笔记2-关于回归参数w的先验的理解
接上篇,现在考虑给w\boldsymbol{w}w加入先验,考虑最简单的假设,也就是w\boldsymbol{w}w服从均值为0,协方差矩阵为α−1I\alpha^{-1}\boldsymbol{I}α−1I的高斯分布。 p(w∣α)N(w∣0,α−1I)(α2π)(M1)/2exp{−α2wTw}\begin{…...

Selenium原理
我们使用Selenium实现自动化测试,主要需要3个东西1.测试脚本,可以是python,java编写的脚本程序(也可以叫做client端)2.浏览器驱动, 这个驱动是根据不同的浏览器开发的,不同的浏览器使用不同的webdriver驱动…...

Disconf、Apollo和Nacos分布式配置框架差异对比
差异对比表格: 功能点DisconfApolloNacos依赖高可用框架完全依赖于Zookeeper来实现监听拉取,向外提供了HTTP拉取数据接口依赖于Eureka实现内部服务发现注册,提供HTTP接口给Client SDK拉取监听数据内部自研实现框架高可用CAP理论偏重点Zookee…...

高新技术企业认定条件条件 高企认定要求
高新技术企业认定条件 一、成立年限:申报企业须注册成立365个日历天数,而非一个会计年度。 二、知识产权 (1)申报企业必须拥有在中国境内授权或审批审定的知识产权,且知识产权在有效保护期内。知识产权权属人应为申请企…...
 | 机试题+算法思路+考点+代码解析 【2023】)
华为OD机试 - 新学校选址(JavaScript) | 机试题+算法思路+考点+代码解析 【2023】
新学校选址 题目 为了解新学期学生暴涨的问题,小乐村要建立所新学校 考虑到学生上学安全问题,需要所有学生家到学校的距离最短. 假设学校和所有学生家都走在一条直线之上,请问学校建立在什么位置, 能使得到学校到各个学生家的距离和最短 输入 第一行: 整数 n 取值范围 [1,1…...

二进制部署K8S
目录 一、环境准备 1、常见的k8s部署方式 2、关闭防火墙 3、关闭selinux 4、关闭swap 5、根据规划设置主机名 6、在master添加hosts 7、将桥接的IPv4流量传递到iptables的链 8、时间同步 二、部署etcd集群 1、master节点部署 2、查看证书的信息 2.1 创建k8s工作目…...

高效获知Activity的生命周期
Activity生命周期监听 使用 Instrumentation 对 Activity 生命周期进行监听。 优点: 全局仅一次反射,性能影响极小所有Activity的生命周期都能够被监听到由于Java的单继承,为了拓展性,可以使用装饰器模式对Instrumentation进行功…...

分析现货黄金价格一般有什么方法
分析现货黄金价格一般有什么方法呢?我相信很多投资者都会说,是技术分析。很多人并不知道技术分析是什么,并且技术分析是如何去分析现货黄金价格的,那么本文就介绍一下技术分析的主要分类。可以说,小编的其他文章都是以…...
Spring中的拦截器
这里写目录标题基本概念HandlerInterceptor拦截器HandlerInterceptor讲解MethodInterceptor拦截器二者的区别基本概念 在web开发中,拦截器是经常用到的功能。它可以帮我们预先设置数据以及统计方法的执行效率等等。 Spring中拦截器主要分两种,一个是Han…...

【Linux操作系统】【综合实验四 Linux的编译环境及线程编程】
文章目录一、实验目的二、实验要求三、实验内容四、实验报告要求一、实验目的 要求熟悉Linux环境中的程序编译、调试与项目管理过程并能实现具体操作;熟练使用基础函数库中与线程库中的管理函数,实现用户线程编程过程,并深入了解Linux的线程…...

Switch 如何使用NSCB 转换XCI NSP NSZ教程
很多小白经常碰到Switch游戏文件格式和预期不符的情况,比如碰到nsz自己不会安装(安装NSZ格式文件教程);或者是碰到xci格式的,想转换为nsp;抑或想将nsz格式文件还原回nsp格式。本文对此提供了解决方案。 文中…...
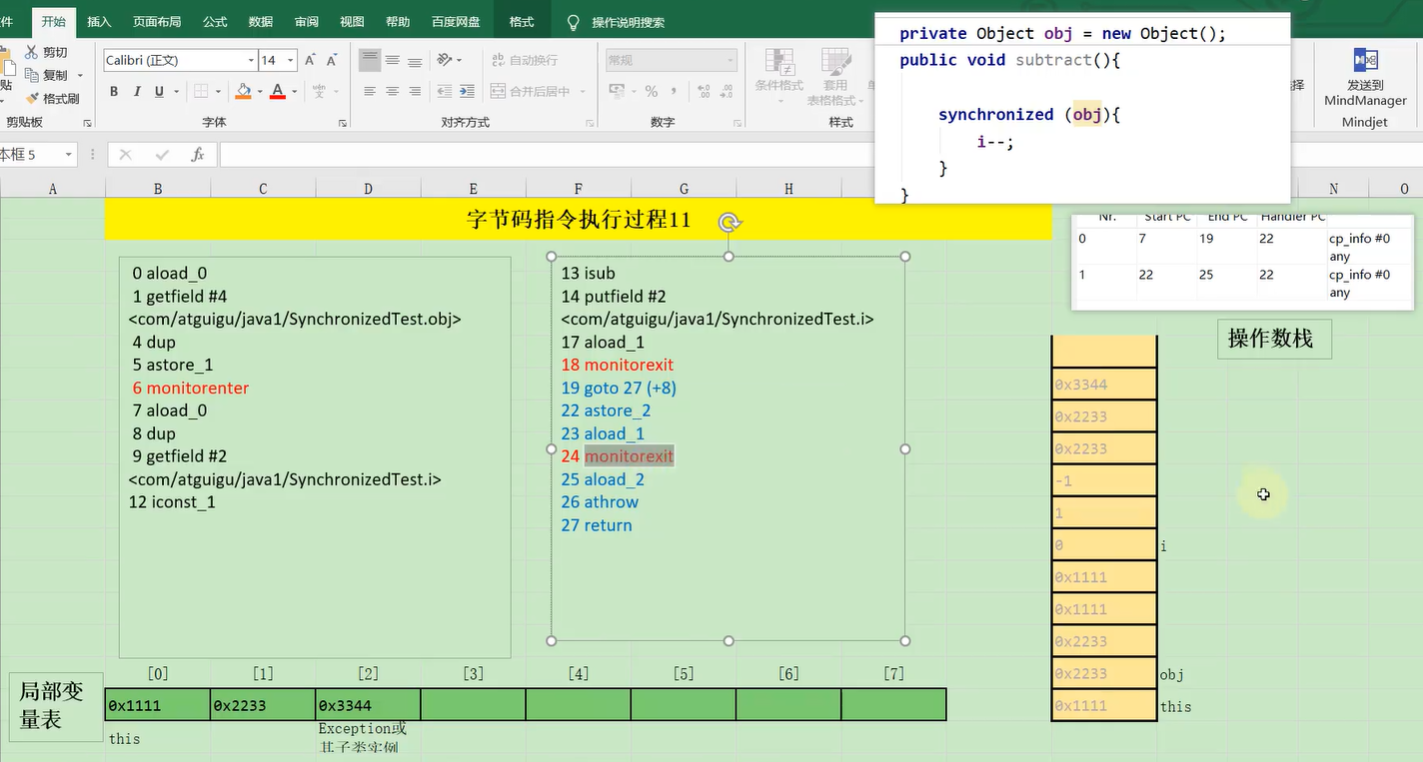
JVM12 字节码指令集
1. 概述 2. 加载与存储指令 2.1. 局部变量压栈指令 iload 从局部变量中装载int类型值 lload 从局部变量中装载long类型值 fload 从局部变量中装载float类型值 dload 从局部变量中装载double类型值 aload 从局部变量中装载引用类型值(refernce) iload_0 从…...

centos之python安装与多版本python之间的共存
一、背景 随着python版本迭代加快,有写python模块再低版本无法运行,此时需要我们在进行安装一个python版本 例如:uvloop 在python3.7上运行;python 3.6官方不再维护与更新 有些模块或不支持较低版本、有些模块支持较高版本python…...
)
SpringBoot学习笔记(一)
Idea中隐藏指定文件或指定类型文件 setting->File Types->Ignored Files and Folders输入要隐藏的文件名,支持*号通配符回车确认添加 SpringBoot概述 parent 小结: 开发SpringBoot程序要继承spring-boot-starter-parentspring-boot-starter-pa…...

美国原装KEYSIGHT E4981A(安捷伦) E4981A电容计
KEYSIGHT E4981A(安捷伦) Keysight E4981A(安捷伦)电容计为生产线中的陶瓷电容器测试提供了高速、可靠的测量。E4981A 实现了电容从小到大的测量能力,测量准确。Agilent E4981A 电容计有助于提高测试吞吐量࿰…...
K8S的基础概念
目录 一、k8s概述 1、k8s简介 1.1 k8s的作用 1.2 k8s的由来 1.3 k8s的含义 1.4 k8s的官网 1.5 GitHub 2、为什么要用 K8S? 2.1 K8s的目标 2.2 K8s解决了裸跑Docker 的若干痛点: 2.3 K8s的主要功能 3、K8s的特性 二、Kubernetes 集群架构与组件 1、工作流程 2、…...

【数据结构】——环形队列
文章目录一.环形队列的定义及其特点二.使用数组来实现环形队列1.创建一个队列2.初始化队列3. 判断环形队列是否为空4.判断环形队列是否已满5. 向循环队列插入元素,插入成功返回真6.删除环形链表的数据7. 取队头元素8.取队尾元素8.释放空间总结一.环形队列的定义及其…...
windows 安装Qt
下载 下载地址https://download.qt.io/,此文已5.7.0为例子。 根据图片依次选择即可。 安装 安装过程参考另一篇文章Ubuntu 安装 Qt5.7.0即可 配置环境变量 ps:我就是之前没配置环境变量,直接使用创建项目,项目源码直接运行是…...
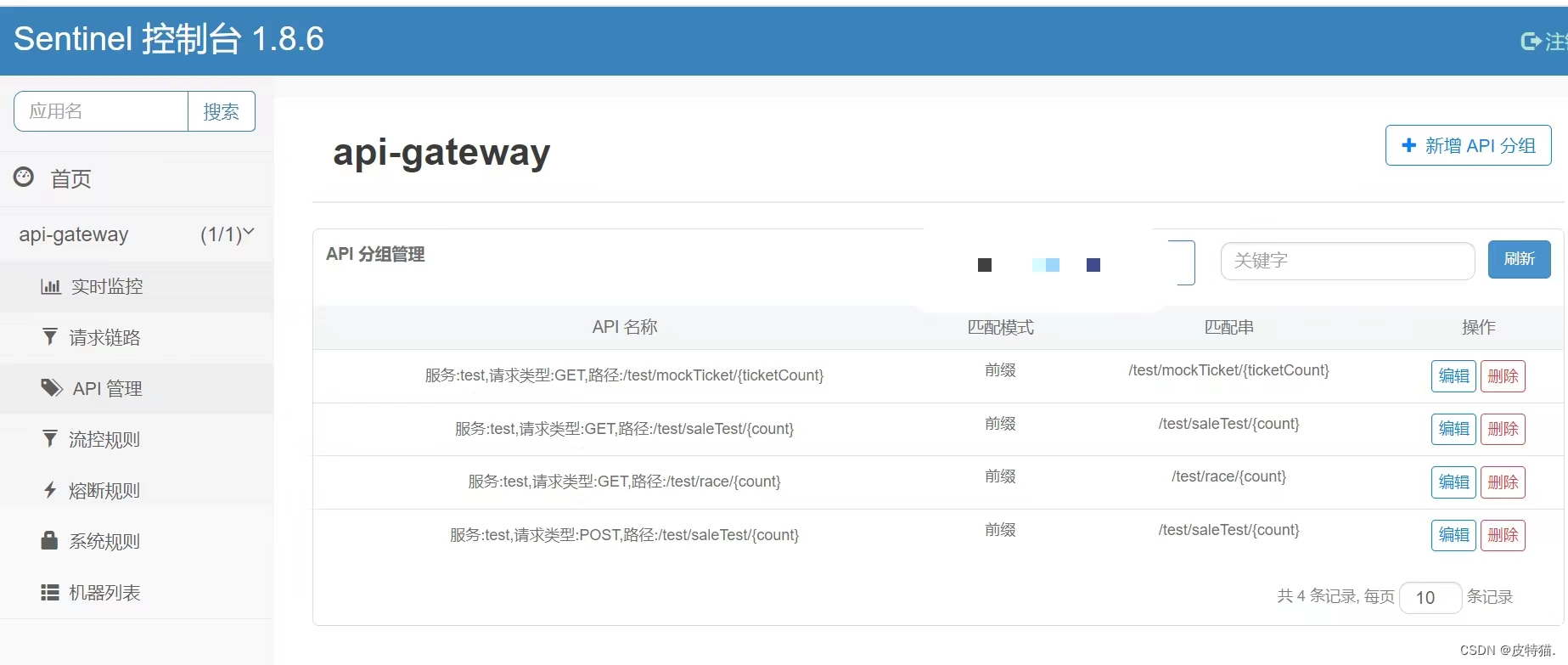
spring cloud gateway集成sentinel并扩展支持restful api进行url粒度的流量治理
sentinel集成网关支持restful接口进行url粒度的流量治理前言使用网关进行总体流量治理(sentinel版本:1.8.6)1、cloud gateway添加依赖:2、sentinel配置3、网关类型项目配置4、通过zk事件监听刷新上报api分组信息1、非网关项目上报api分组信息…...
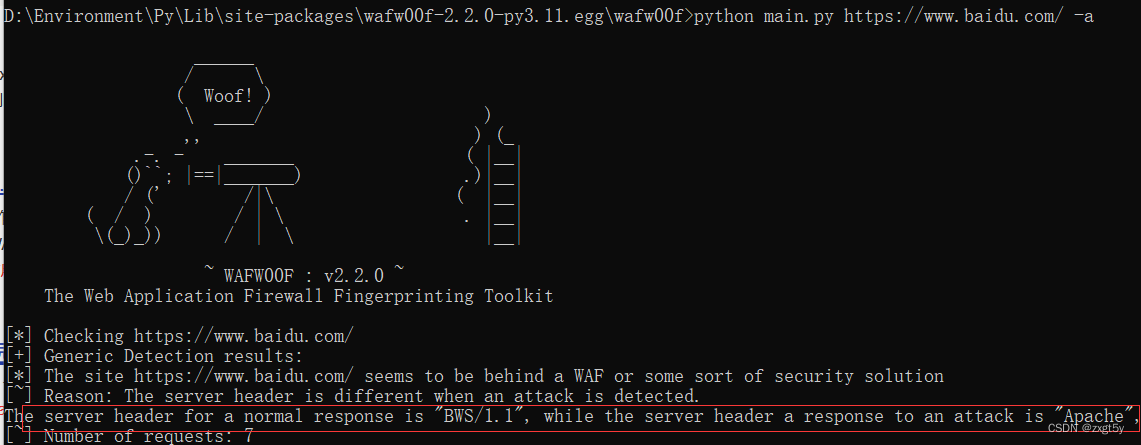
wafw00f工具
wafw00f Web应用程序防火墙指纹识别工具 github地址:https://github.com/EnableSecurity/wafw00f 安装环境:python3环境 —>使用 pip install wafw00f 进行安装 安装成功后目录:python安装目录中的Lib\site-packages\wafw00f 本机为&a…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
