谷歌面试-扔鸡蛋
今天想跟大家分享一个有意思的面试题,这让我再一次感叹思维的奇妙,接下来我们一起看看吧~
首先来看看题目:
你有2颗鸡蛋,需要以最少的尝试次数来判断在100层的高楼上,哪一层楼是鸡蛋的安全层。
换句话说,就是需要确定我们从哪一层楼扔鸡蛋下去,鸡蛋恰好不会摔碎。高于安全层鸡蛋都会碎,低于安全层都不会碎。比如鸡蛋在第1层没有摔碎,在第2层摔碎了,那么鸡蛋的安全层就是第1层。
这里有几个假设条件:
-
没有摔碎的鸡蛋可以重复使用;
-
每颗鸡蛋的坚硬程度都是相同的。

这道题乍一看挺简单的,但其实解答相对复杂,而且解法多种多样,要在面试时逻辑清楚地表达完整思路,不仅要求面试者的知识储备要广、反应能力要快,逻辑思维和语言表达能力也是必不可少的。
成为经典可谓当之无愧。
解法1:简单粗暴
我们先来个最省事儿的方法:假设我们只有一颗鸡蛋,显然只有从一楼开始扔,逐层试探,直到鸡蛋摔碎,安全层就是第N-1层。
但是缺点想必大家也看出来了,这是拼运气啊,最坏情况需要扔100次。
用一颗鸡蛋的方法虽然简单粗暴,但也是给两颗鸡蛋的情况缕清一些思路。
简单写一下如何实现:
// 假设arr表示100层楼,每层楼鸡蛋会不会碎,如果arr[i] === 1 表示i层楼的鸡蛋会碎,arr[i] === 0表示第i层楼的鸡蛋不会碎// 简单暴力
const throwEggs1 = (arr) => {for(let i = 1; i <= 100; i++) {if (arr[i] === 1) {return i}}
}
解法2:常规二分
有两颗鸡蛋,二分法想必是大多数同学脑海里浮现的第一个念头吧?
我们先从50楼扔一颗鸡蛋,如果没碎,就往上继续二分,到75楼继续扔······
这是比较顺利的情况,如果不顺利呢,比如我们从50楼扔鸡蛋,直接碎了,那就只有一颗鸡蛋了。
这时候我们就回到解法1了,只能从1楼开始遍历,又是拼运气的时候了,要是运气好,1楼鸡蛋就没了,那测试次数就是1+1=2次,但最坏情况就是1+49=50次。
这么多次,显然是不能通过google面试的。
// 常规二分const throwEggs2 = (arr) => {let left = 1let right = 100let mid = 0while(left <= right) {mid = Math.floor(left + right) / 2if (arr[mid] === 0) {left = mid + 1} else {right = mid - 1}}return mid
}
解法3:均衡切割
虽然二分法不够优秀,但体现了切分范围的思想。
我们的基本思路是,将100层切分成两个维度,由两个鸡蛋分别控制一个维度。
一个维度是用第一颗鸡蛋分金定穴,另一个维度是用第二颗鸡蛋在前蛋的基础上进行遍历。
换言之,我们是将100层切分成若干个区块,由第一颗鸡蛋确定最高安全楼层所属的区块,再由第二颗鸡蛋逐层确定其具体的位置。
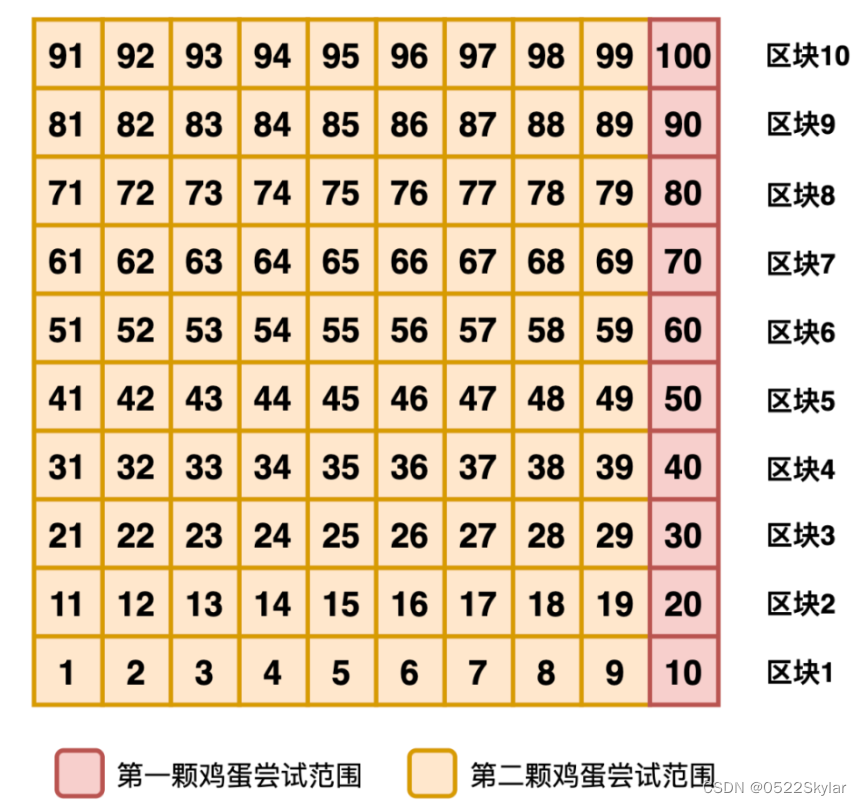
在1-100层楼之间,假设我们从上往下尝试,即从100层开始扔第一颗蛋,大概率是碎了,那第二颗蛋便又回到了解法1。
所以,我们应该从下往上进行划分、尝试,这样即使第一颗鸡蛋碎了,用第二颗蛋遍历的成本也比较低。
比如第一颗蛋每10层扔一次,第一次从10层扔,第二次从20层扔,第三次从30层扔……一直扔到100层。
第二颗蛋就只用在第一颗蛋摔碎的层数和前一次的安全层之间的9层进行范围遍历。
也就是说,要是第一颗鸡蛋在第30层摔碎了,那就拿第二颗蛋从21层到29层逐层尝试。
这样的最好情况就是第一颗蛋在第10层碎掉,总的尝试次数为1+1=2次。
最坏的情况是在第100层碎掉,总尝试次数为10+9=19次。
// 均衡切割
const throwEggs3 = (arr) => {let count = 0// 第一个鸡蛋for (let i = 1; i < 10; i++) {if (arr[i * 10] === 1) {count = i * 10break}}// 第二个鸡蛋for(let i = count - 1; i >= count - 10; i--) {if (arr[i] !== 1) {return i}}
}
解法4:微妙平衡
上面的方法,看似已经比较完美了。
但是我们再具像化一点,就能发现问题:第一颗鸡蛋能快速定位安全楼层低的情况,但如果安全楼层位置越高,耗时就会越久,而第二颗鸡蛋在每个区块内的消耗,都是一样的。
如果鸡蛋的最高安全层为18或者98,用解法3的思路的话,这两种情况的总尝试次数并不一样:
最高安全楼层为18时,第一颗鸡蛋试了2次就定位了区块;而最高安全楼层为98时,第一颗鸡蛋试了10次才定位了区块。
虽然第二颗鸡蛋在区块内部的逐层尝试次数是一样的,但98层对应的总尝试次数就多太多了。
原因就是区块完全均匀划分对大数不利。
明白了这个缺陷,也就知道了改进的基本思想:要对100找出一种二维区块划分,但不是均匀划分。
对于比较小的区块部分,其包含的楼层范围可以适当增加;越向大数部分走,其包含的楼层范围越来越小。从下往上,每一个区块内所含楼层递减。
在最高安全楼层比较低的情况下,第一颗鸡蛋尝试的次数少;在最高安全楼层比较高的情况下,则第二颗鸡蛋尝试的次数少。
就是用第二颗鸡蛋尝试次数的减少来弥补第一颗鸡蛋需要的尝试次数的递增,使两颗鸡蛋在不同维度上的尝试次数此消彼长,达到一种总体上的平衡。
每上一个区块,第一颗鸡蛋消耗的次数就+1,我们索性就假设每个区块包含的楼层数逐级递减1,以达到平衡。
那么每个区块包含的层数应该如何划分呢?
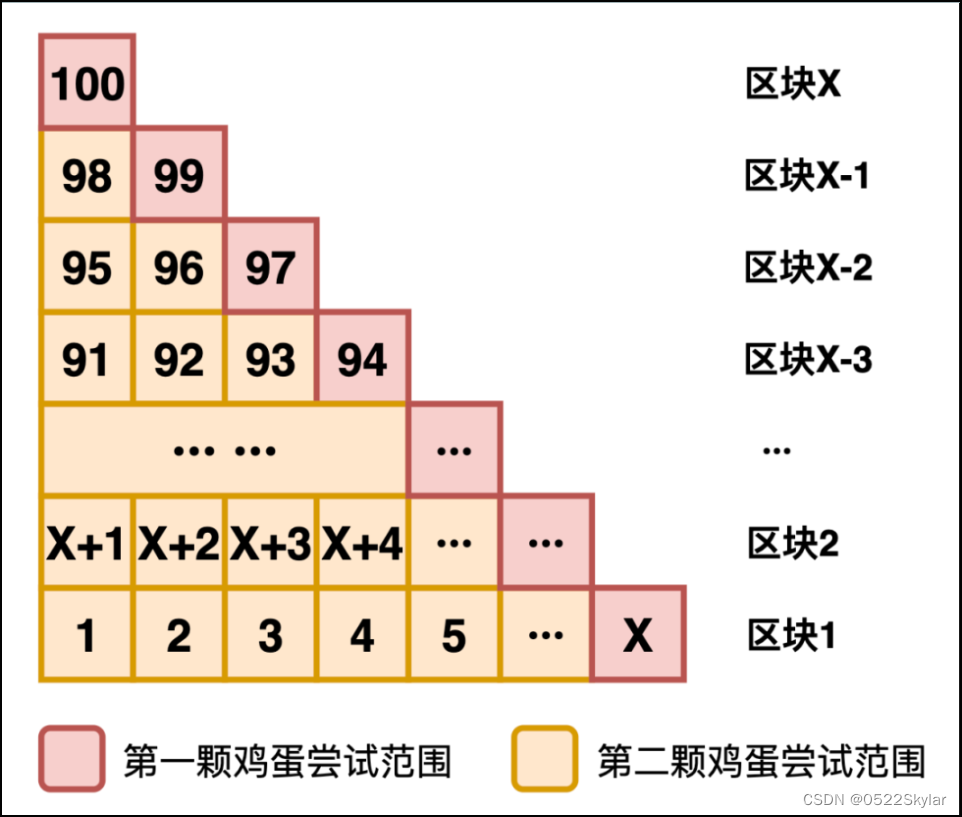
我们假设第一个区块有X层,那么第二个就是X-1,以此类推,我们就得到了一个方程式:
X+(X-1)+(X-2)+···+3+2+1≥100
可以看出来,这时候区块个数和第一个区块包含的层数其实是相等的。
现在我们回过头来,再仔细看看方程式,是不是有点熟悉,不就是等差数列求和么!
所以我们化简方程式:
X(X+1)/2≥100
这里X最小值我们向上取整,得到14。
有同学会问为什么一定到1呢,最后一个区块一定只有1层吗?
不是的,到1是表示在X个区块的情况下,最多能覆盖的层数。
比如我们这个例子,X是14,求出的楼层总数是105,也就是可以覆盖105层,题目要求的100层当然绰绰有余。
由此,第一个区块包含14层楼,即1到14层;
第二个区块包含13层楼,即15到27层;
第三个区块包含12层楼,即28到39层;
······
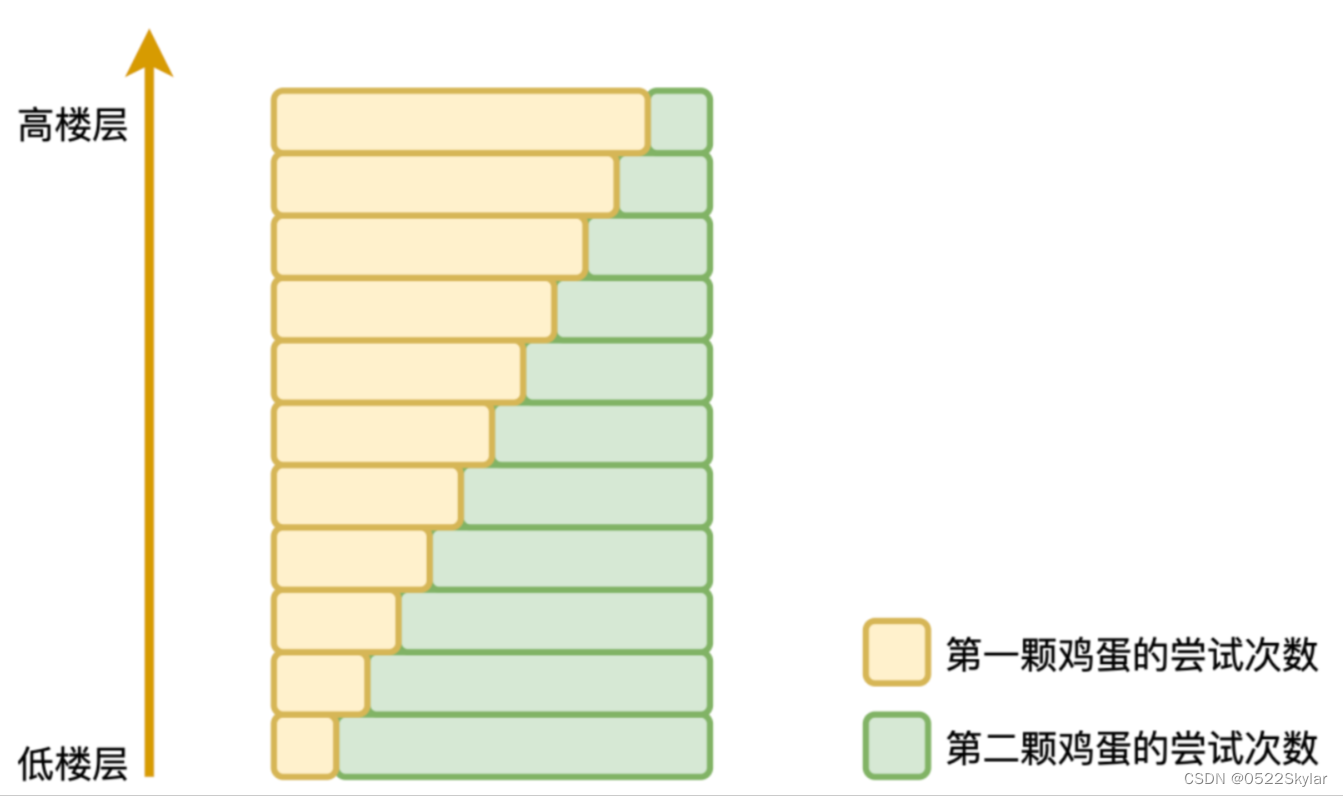
第一颗鸡蛋依次试第14、27、39、50、60、69、77、84、90、95、99、100层。只要期间任何一次鸡蛋碎了,就拿第二颗鸡蛋从上一次的安全层之后开始逐层尝试,直至第二颗鸡蛋也摔碎为止。
用这个方法,总次数一定不会超过14次。
因为最高安全楼层越高,第一颗鸡蛋的尝试次数也就越多,但第二颗鸡蛋的尝试次数随之越来越少,两者始终维持着一种微妙的平衡,最后总的尝试次数波动也不会太大。
下面是全部的代码实现:
// 假设arr表示100层楼,每层楼鸡蛋会不会碎,如果arr[i] === 1 表示i层楼的鸡蛋会碎,arr[i] === 0表示第i层楼的鸡蛋不会碎// 暴力
const throwEggs1 = (arr) => {for(let i = 1; i <= 100; i++) {if (arr[i] === 1) {return i}}
}// 常规二分const throwEggs2 = (arr) => {let left = 1let right = 100let mid = 0while(left <= right) {mid = Math.floor(left + right) / 2if (arr[mid] === 0) {left = mid + 1} else {right = mid - 1}}return mid
}// 均衡切割
const throwEggs3 = (arr) => {let count = 0// 第一个鸡蛋for (let i = 1; i < 10; i++) {if (arr[i * 10] === 1) {count = i * 10break}}// 第二个鸡蛋for(let i = count - 1; i >= count - 10; i--) {if (arr[i] !== 1) {return i}}
}// 微妙平衡
const throwEggs4 = (arr) => {let block = 10let count = 0// block(block + 1) / 2 >= 100while(block * block + block < 100 * 2) {block++}// 第一个鸡蛋的尝试let temp = block // 每层区块的最后一个while(temp <= 100) {if (arr[temp] === 1) {count = tempbreak}--blocktemp += block}// 第二个鸡蛋的尝试for(let i = count - 1; i >= count - block; i--) {if (arr[i] === 0) {return i}}
}
除了文中我们讨论的解法,这道题也还有其他解法可以选择,如果感兴趣大家可以自己研究研究,也欢迎来一起讨论!
凭心而论,要是在毫无准备的情况下,一般人只能想到第一种,做过算法题的,应该能够想到第二种,想到解法三已经是最优解了,能在这么短的时间内想到解法四的大神是凤毛麟角。
好了,祝大家周末愉快!
最后,希望大家读完这篇文章都能有所收获!
相关文章:

谷歌面试-扔鸡蛋
今天想跟大家分享一个有意思的面试题,这让我再一次感叹思维的奇妙,接下来我们一起看看吧~ 首先来看看题目: 你有2颗鸡蛋,需要以最少的尝试次数来判断在100层的高楼上,哪一层楼是鸡蛋的安全层。 换句话说,…...
Unity血条制作
一、使用UGUI制作血条 我一般使用image制作血条,当然,也可以使用滑动组件Slider。image的具体操作步骤如下 普通血条 1、在Hierarchy面板中,创建两个image组件,将其中一个设置为另外一个的子节点 2、在Inspector面板中&#…...

vue,uniapp生成二维码
话不多说直接开干 先是vue的 1,首先按照一下依赖 npm install --save qrcode 2,在需要使用的页面引入 import QRCode from qrcode; 3,使用 const codeDetail (item) > {//这个item.code是要生成的数据,我的是一串数字QRCode.toDataURL(item.co…...
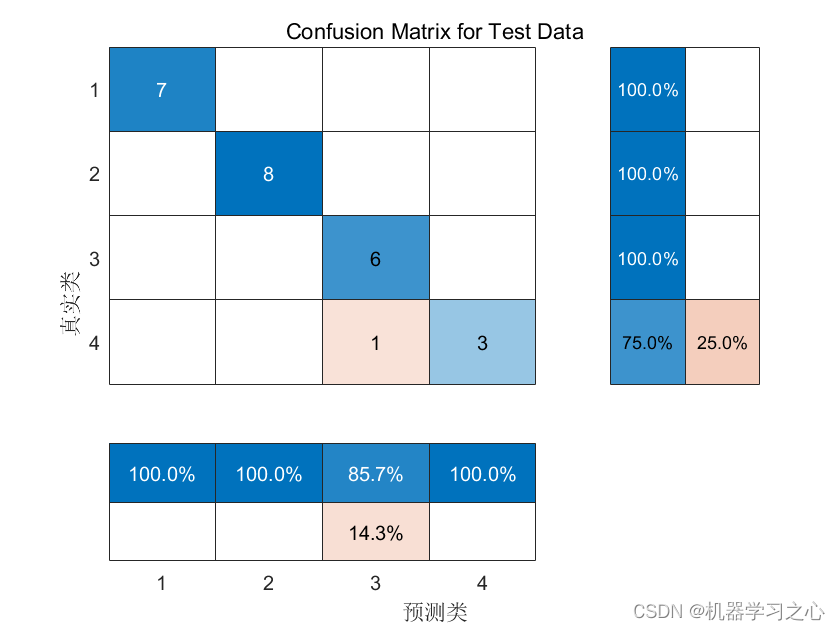
分类预测 | MATLAB实现SSA-CNN-SVM基于麻雀算法优化卷积支持向量机分类预测
分类预测 | MATLAB实现SSA-CNN-SVM基于麻雀算法优化卷积支持向量机分类预测 目录 分类预测 | MATLAB实现SSA-CNN-SVM基于麻雀算法优化卷积支持向量机分类预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 MATLAB实现SSA-CNN-SVM基于麻雀算法优化卷积支持向量机分类预测…...
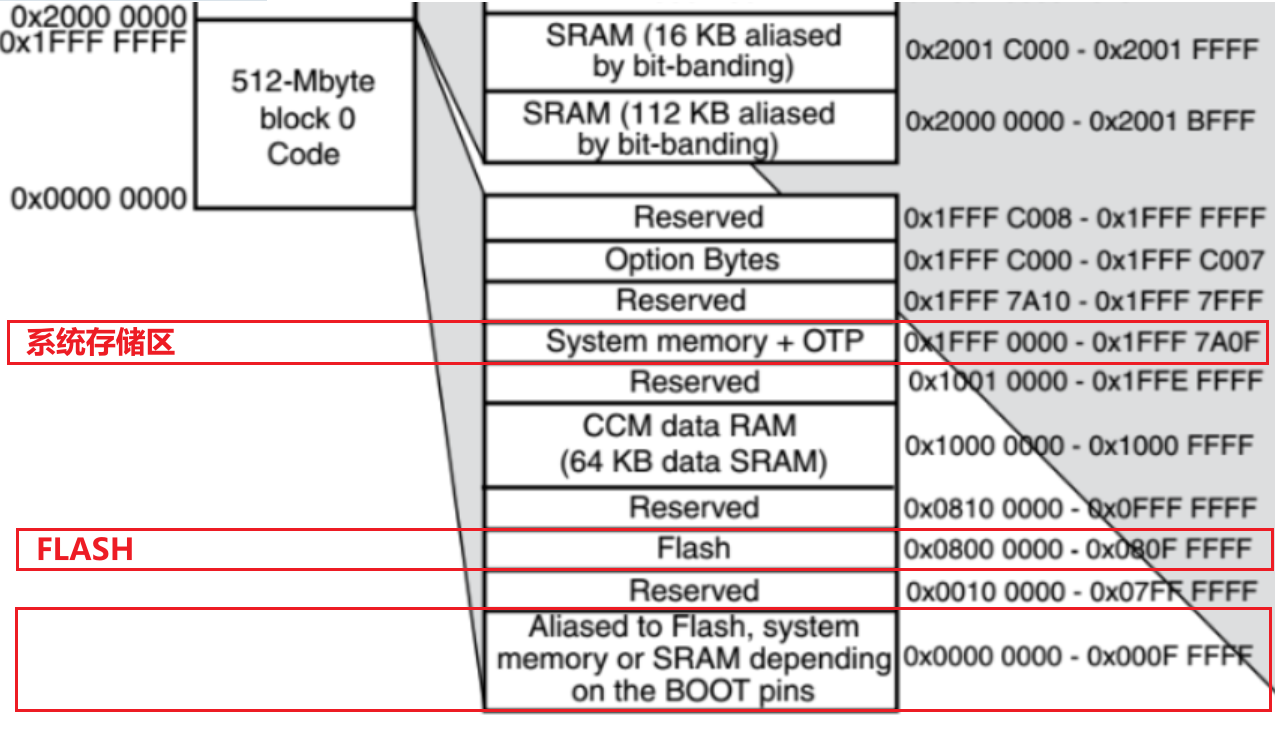
STM32启动模式详解
文章目录 前置知识1. 单片机最小系统组成2. BOOT电路3. 三种启动模式4. 存储器映射 从主FLASH启动从系统存储区启动从SRAM启动 前置知识 1. 单片机最小系统组成 一个单片机最小系统由电源、晶振、下载电路、BOOT电路、和复位电路组成。少一个单片机都启动不了。 2. BOOT电路 …...
go语言中的切片
切片底层 切片(Slice)是一个拥有相同类型元素的可变长度的序列。它是基于数组类型做的一层封装。它非常灵活,支持自动扩容。 切片是一个引用类型,它的内部结构包含地址、长度和容量。切片一般用于快速地操作一块数据集合。 切片…...
HTML-常见标签、HTML5新特性
HTML 软件架构 1.C/S架构 (1) C/S架构即Client/Server(客户机/服务器)结构。 (2) C/S 架构特点 C/S结构在技术上很成熟,它的主要特点是交互性强、具有安全的存取模式、网络通信量低、响应速度快、利于处理大量数据。但是该结构的程序是…...

微信有自己的“知乎”,微信问一问来了!
这几个月来,微信问一问一直挺火的,有人涨粉,有人变现,有人引流~ 这个全新的流量入口对流量玩家来说又是一波巨大的流量红利。 微信问一问就类似于微信版的知乎,未来将对知乎产生一定竞争压力。 依托于微信这个庞大的流…...
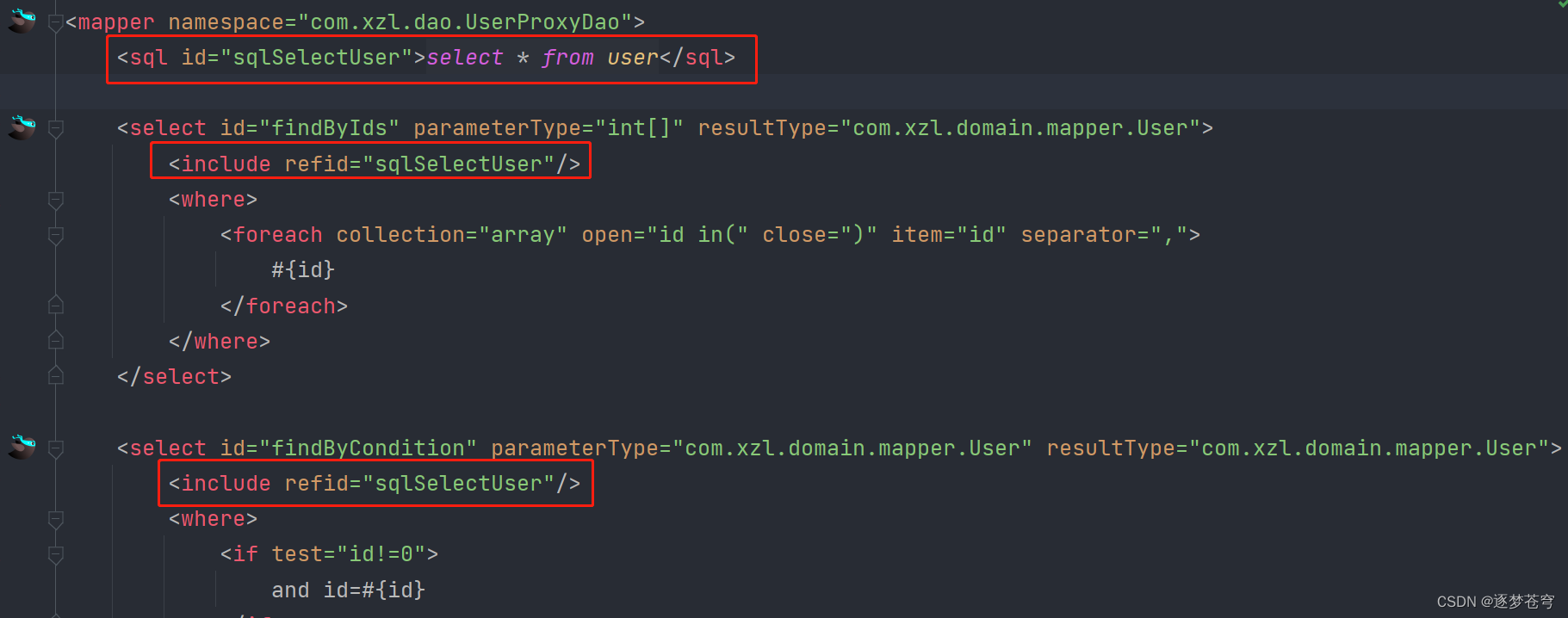
[MyBatis系列③]动态SQL
目录 1、简介 2、if标签 3、foreach标签 4、SQL抽取 ⭐MyBatis系列①:增删改查 ⭐MyBatis系列②:两种Dao开发方式 1、简介 开发中在MyBatis映射文件配置SQL语句,但是前面配置的都是比较简单的,不涉及稍复杂的业务场景。想要应…...
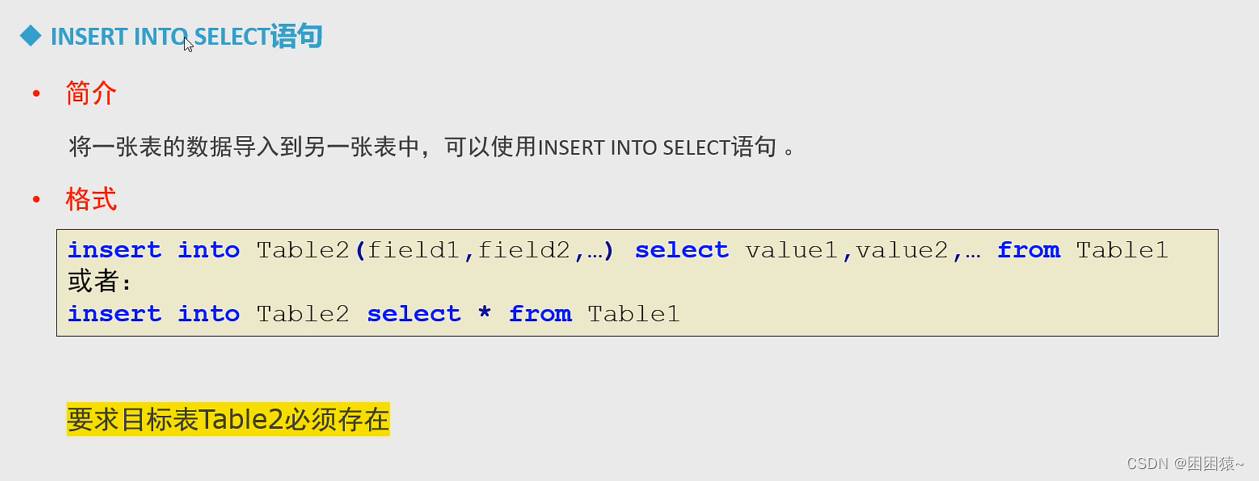
开始MySQL之路—— DDL语法、DML语法、DQL语法基本操作详解
DDL语法 DDL(Data Definition Language) 数据定义语言,该语言部分包括以下内容。 对数据库的常用操作 对表结构的常用操作 修改表结构 对数据库的常用操作 1: 查看当前所有的数据库 show databases; 2:创建数据库 create dat…...
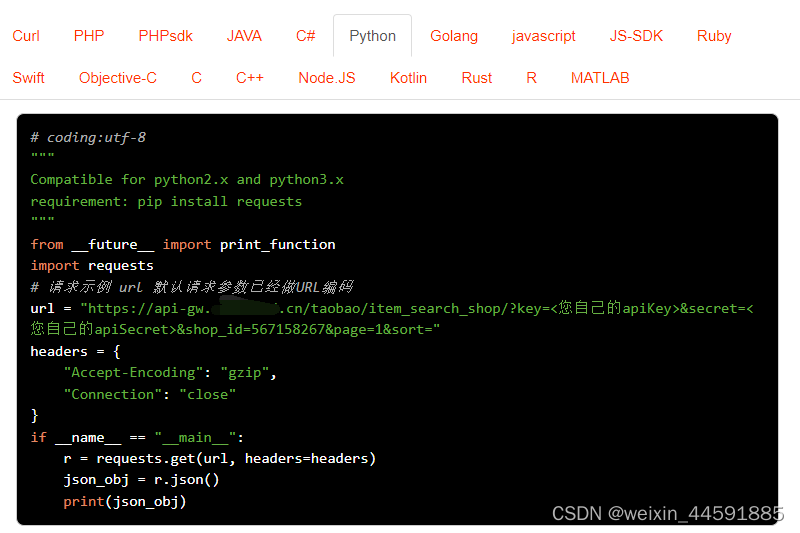
Java“牵手”天猫整店商品API接口数据,通过店铺ID获取整店商品详情数据,天猫店铺所有商品API申请指南
天猫平台店铺所有商品数据接口是开放平台提供的一种API接口,通过调用API接口,开发者可以获取天猫整店的商品的标题、价格、库存、月销量、总销量、库存、详情描述、图片、价格信息等详细信息 。 获取店铺所有商品接口API是一种用于获取电商平台上商品详…...

用AI重构的钉钉,“钱”路在何方?
点击关注 文|郝 鑫,编|刘雨琦 钉钉2023年生态大会,离开了两年的无招,遇到了单飞9天的钉钉。 “做小钉钉、做好钉钉、做酷钉钉”,无招重申了钉钉的方向。 无招提到的三点,再加上“高质量增长”…...

批量根据excel数据绘制柱状图
要批量根据Excel数据绘制柱状图,可以使用Python中的pandas和matplotlib库来实现。下面是示例代码: import pandas as pd import matplotlib.pyplot as plt import os def draw_bar_chart_from_excel(file_path, x_column, y_column, output_folder): …...

浅谈 Java 中的 Lambda 表达式
更好的阅读体验 \huge{\color{red}{更好的阅读体验}} 更好的阅读体验 Lambda 表达式是一种匿名函数,它可以作为参数传递给方法或存储在变量中。在 Java8 中,它和函数式接口一起,共同构建了函数式编程的框架。 什么是函数式编程 函数式编程是…...

闭包的概念
概念 内层函数可以访问到外层函数的变量和参数,即一个函数和它周围状态捆绑在一起的组合。 举例 函数作为返回值 // 函数作为返回值 function test(){const a 1;return function() {console.log(a:,a);} }const fn test(); const a 6; fn(); // 1 2. 函数作…...

openGauss学习笔记-52 openGauss 高级特性-LLVM
文章目录 openGauss学习笔记-52 openGauss 高级特性-LLVM52.1 适用场景52.2 非适用场景52.3 其他因素对LLVM性能的影响52.4 LLVM使用建议 openGauss学习笔记-52 openGauss 高级特性-LLVM openGauss借助LLVM(Low Level Virtual Machine)提供的库函数&…...

MySQL 8.0字符集校正
MySQL升级为8.0版本时,之前版本的字符集往往是不同的,需要校正。 执行下面的三个SQL语句的查询结果,可以从库、表、列三个层面对字符集进行校正。 库 select concat(alter database , schema_name, default character set utf8mb4 collate …...

软考:中级软件设计师:数据库恢复与备份,故障与恢复,反规范化
软考:中级软件设计师:数据库恢复与备份 提示:系列被面试官问的问题,我自己当时不会,所以下来自己复盘一下,认真学习和总结,以应对未来更多的可能性 关于互联网大厂的笔试面试,都是需要细心准备…...
Unbutu系统-Docker安装、JDK环境配置,Docker常用指令、Docker安装MySQL、Redis、Tomcat、Nginx,前端后分离项目部署
目录 1、防火墙 1.1、查看防火墙状态 1.2、开启防火墙 1.3、关闭防火墙 1.4、重启防火墙 1.5、查看防火墙版本 2、安装JDK 2.1、官网下载tar包 2.3、解压tar.gz文件 2.4、配置环境变量 2.4.1、查看安装路径 2.4.2、设置环境变量 2.4.3、执行该让环境变量生效 2.4…...

Python绘图系统10:在父组件中使用子组件的函数
文章目录 Combobox绑定事件互相调用源代码 Python绘图系统: 📈从0开始实现一个三维绘图系统自定义控件:坐标设置控件📉坐标列表控件📉支持多组数据的绘图系统图表类型和风格:散点图和条形图📊混…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...
