Java之初始化顺序实践
功能概述
- 在创建Java对象时,需要将对象中的成员变量进行初始化后,才能调用对象的构造方法创建对象。本文中将会讲解初始化时父类与子类对应的顺序。
功能实践
场景1:父类、子类的初始化顺序
用例代码
@Test
public void test_init_order() {new Child();
}public class Parent {static {System.out.println("父类静态块");}{System.out.println("父类非静态块");}public Parent() {System.out.println("父类构造方法");}
}public class Child extends Parent {static {System.out.println("子类静态块");}{System.out.println("子类非静态块");}public Child() {System.out.println("子类构造方法");}
}
结果输出
父类静态块
子类静态块
父类非静态块
父类构造方法
子类非静态块
子类构造方法
结果分析
- 先初始化静态块:父类的静态块 -> 子类的静态块。
- 再初始化非静态块以及构造方法:
- 父类的非静态块 -> 父类的构造方法
- 子类的非静态块 -> 子类的构造方法
场景2:块、成员域中初始化顺序
用例代码
static {a = 2;} //静态块中初始化
static int a = 1; //成员域中初始化
static int b = 3;static {b = 4;}{c = 5;} //可以放在声明的上面
int c = 3;@Test
public void test_order() {System.out.println(a);System.out.println(b);System.out.println(c);
}
结果输出
1
4
3
结果分析
- 块中的初始化与成员域中的初始化是平级的,所以会按照从上到下初始化,最后一次初始化为最终的值。
场景3:静态变量的调用
用例代码
@Test
public void test_static_var() {System.out.println(InitB.c);
}public class InitA {public static String c = "C";static {System.out.println("A");}
}public class InitB extends InitA {static {System.out.println("B");}
}用例输出
A
C
结果分析
- 因为调用InitB.c,static变量c在A类中,所以会加载父类A,所以输出了静态块中的"A"。
- 因为InitB.c直接访问InitA的变量,不需要访问InitB中的其它内容,所以就不要加载InitB了。
功能总结
- 初始化时,执行的顺序为:父类静态变量 -> 父类静态代码块 -> 子类静态变量 -> 子类静态代码块 -> 父类非静态变量 -> 父类非静态代码块 -> 父类构造方法 -> 子类非静态变量 -> 子类的非静态代码块 -> 子类构造方法。
相关文章:

Java之初始化顺序实践
功能概述 在创建Java对象时,需要将对象中的成员变量进行初始化后,才能调用对象的构造方法创建对象。本文中将会讲解初始化时父类与子类对应的顺序。 功能实践 场景1:父类、子类的初始化顺序 用例代码 Test public void test_init_order(…...

静态库与动态链接库,第三方库集成到VS
目录 介绍静态库与动态链接库静态库动态链接库 如何将第三方库集成到VS上VS属性管理器配置静态库配置动态链接库属性管理器其他的内容MKL库的安装boost库的安装 介绍 众所周知,.c文件或者.cpp文件变成.exe文件需要经历四个过程 分别是预处理,编译&#…...

生态经济学领域里的R语言机器学(数据的收集与清洗、综合建模评价、数据的分析与可视化、数据的空间效应、因果推断等)
近年来,人工智能领域已经取得突破性进展,对经济社会各个领域都产生了重大影响,结合了统计学、数据科学和计算机科学的机器学习是人工智能的主流方向之一,目前也在飞快的融入计量经济学研究。表面上机器学习通常使用大数据…...
)
【ROS】自定义消息方面的bug总结(1)
根据需要创建功能包 一类引用ros库函数的一类是自己定义的消息类型 库函数中有的可以直接在创建功能包的时候添加依赖,也可以在CMakeLists.txt中手动添加 catkin_create_pkg crepes roscpp rospy std_msgs nav_msgs sensor_msgs geometry_msgs创建文件夹msg…...

CTF-XXE(持续更新,欢迎分享更多相关知识点的题目)
知识 实例 BUU [PHP]XXE 进来看到 然后一起看 Write BUU XXE COURSE 1 进来看到 一起看 write NSS [NCTF2019]Fake XML cookbook 反正是XXE 直接整 write [NCTF 2019]True XML cookbook 不整花里胡哨,解题在最下面 write 与博主不同,我通过…...

Python工具箱系列(四十一)
使用zip批量压缩文件 前文的代码示例了使用gzip对单个文件进行压缩。本文示例使用更通用的zipfile来批量压缩文件。zipfile也是python内置的库,使用起来非常方便。废话不说,直接上代码示例。 import dbm import glob import zipfile# 保存压缩计划的库名…...
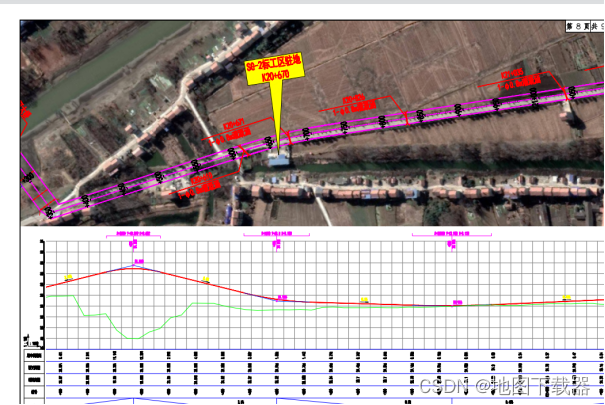
Bigemap在路桥行业是怎么应用的?
选择Bigemap的原因: 奥维下架了,后来了解到的bigemap,于是测试了这款软件 使用场景: 下载影像、矢量路网做前期策划,下载完数据后导出cad ,做一些标注,最终出图下载等高线,作为前期选址依据 …...

代码随想录算法训练营Day48 || ● 198.打家劫舍 ● 213.打家劫舍II ● 337.打家劫舍III
问题1:198. 打家劫舍 - 力扣(LeetCode) 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上…...
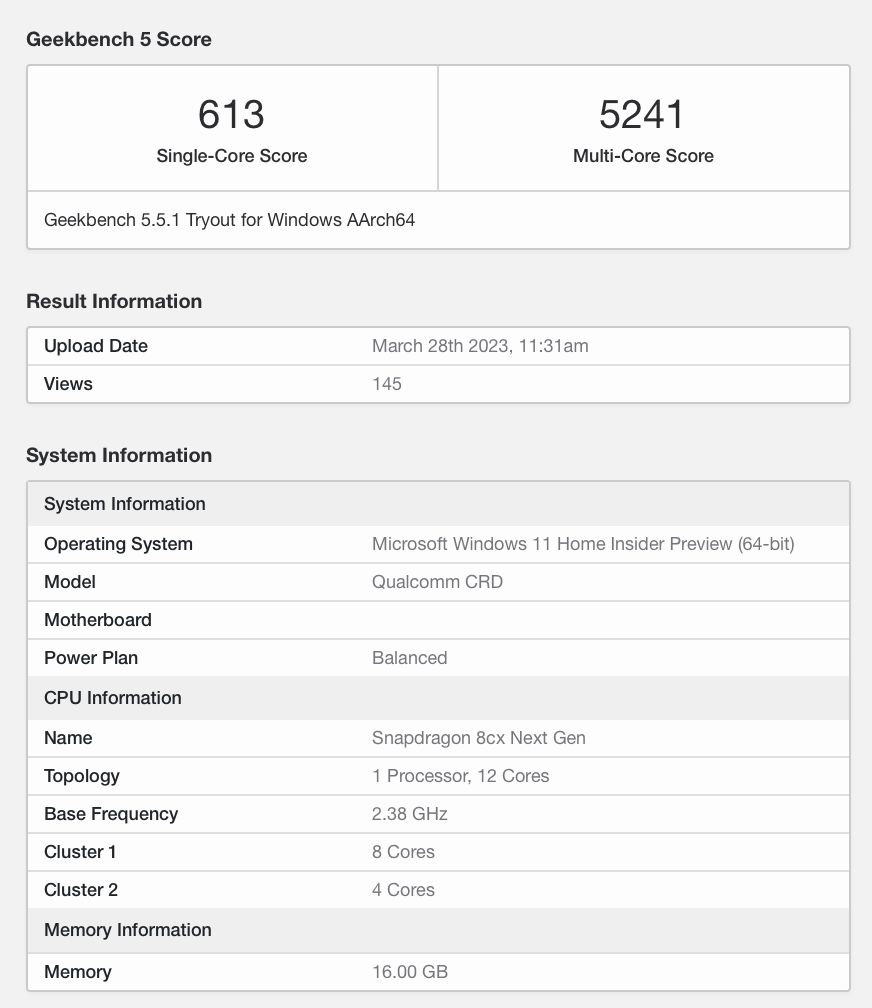
高通面临难题,Oryon核心存在问题,高通8cx Gen 4芯片将推迟发布
"高通公司面临难题,可能会导致骁龙8cx Gen 4的发布时间推迟",关于骁龙8cx Gen 4处理器,还有一些其他值得关注的特点和功能。首先,据悉,骁龙8cx Gen 4采用了高通自家研发的Oryon核心架构,这是一项…...
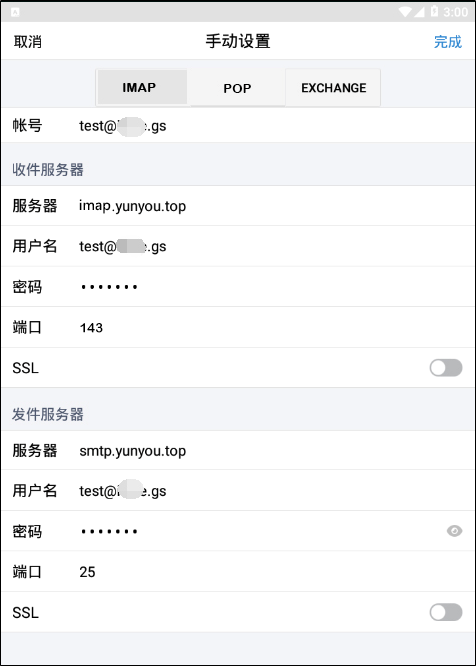
安卓手机如何使用邮箱客户端收发邮件
安卓手机品牌较多,设置界面都不太相同,部分手机常见的如vivo、小米手机都是直接填写邮箱用户名和密码,软件自动设置,即可登录邮箱,其他安卓手机或者第三方安卓手机软件有时候需要手动设置,此处以安卓手机的…...

对java中的List进行深拷贝,并进行删除测试
List<String> list new ArrayList<>(); // 需要拷贝的原始List list.add("aaa"); list.add("bbb"); list.add("ccc"); List<String> listNew new ArrayList<>(); // 新List // 将原始List的值赋值给新List Co…...

springboot服务注册到Eureka,端口总是默认8080,自己配置端口不生效
这段时间接手了一个公司的老项目,用的是SpringCloud,在我用的时候突然发现有一个服务,注册到Eureka后,界面显示的端口和实际Ribbon调用的实例端口是不一致的,后来我自己写了个端口获取了一下所有的实例信息,…...

LeetCode第11~15题解
CONTENTS LeetCode 11. 盛最多水的容器(中等)LeetCode 12. 整数转罗马数字(中等)LeetCode 13. 罗马数字转整数(简单) LeetCode 11. 盛最多水的容器(中等) 【题目描述】 给定一个长…...

如何编译打包OpenSSH 9.4并实现批量升级
1 介绍 openssh 9.4版本已于8月10号发布,安全团队又催着要赶紧升级环境里的ssh版本,本文主要介绍Centos5、Centos6、Centos7下openssh 9.4源码编译rpm包以及批量升级服务器openssh版本的方法。关注公众号后台回复ssh可获取本文相关源码文件。 https://w…...

AcWing 898. 数字三角形 (每日一题)
大家好 我是寸铁 希望这篇题解对你有用,麻烦动动手指点个赞或关注,感谢您的关注 注意 像数组下标出现i-1的,在循环的时候从i1开始。 关于0x3f3f3f3f和Integer.MAX_VALUE 0x3f3f3f3f:1061109567 Integer.MAX_VALUE:2147483647 在选用Integ…...

深度学习中,batchsize的大小对训练结果有什么影响,如何正确使用
一、影响: Batch size在深度学习训练中起着非常重要的作用,它对训练速度、模型性能、以及模型的泛化能力都有影响。以下是一些主要的影响: 训练速度:较大的batch size可以更充分地利用硬件并行性,从而加快单个epoch的…...
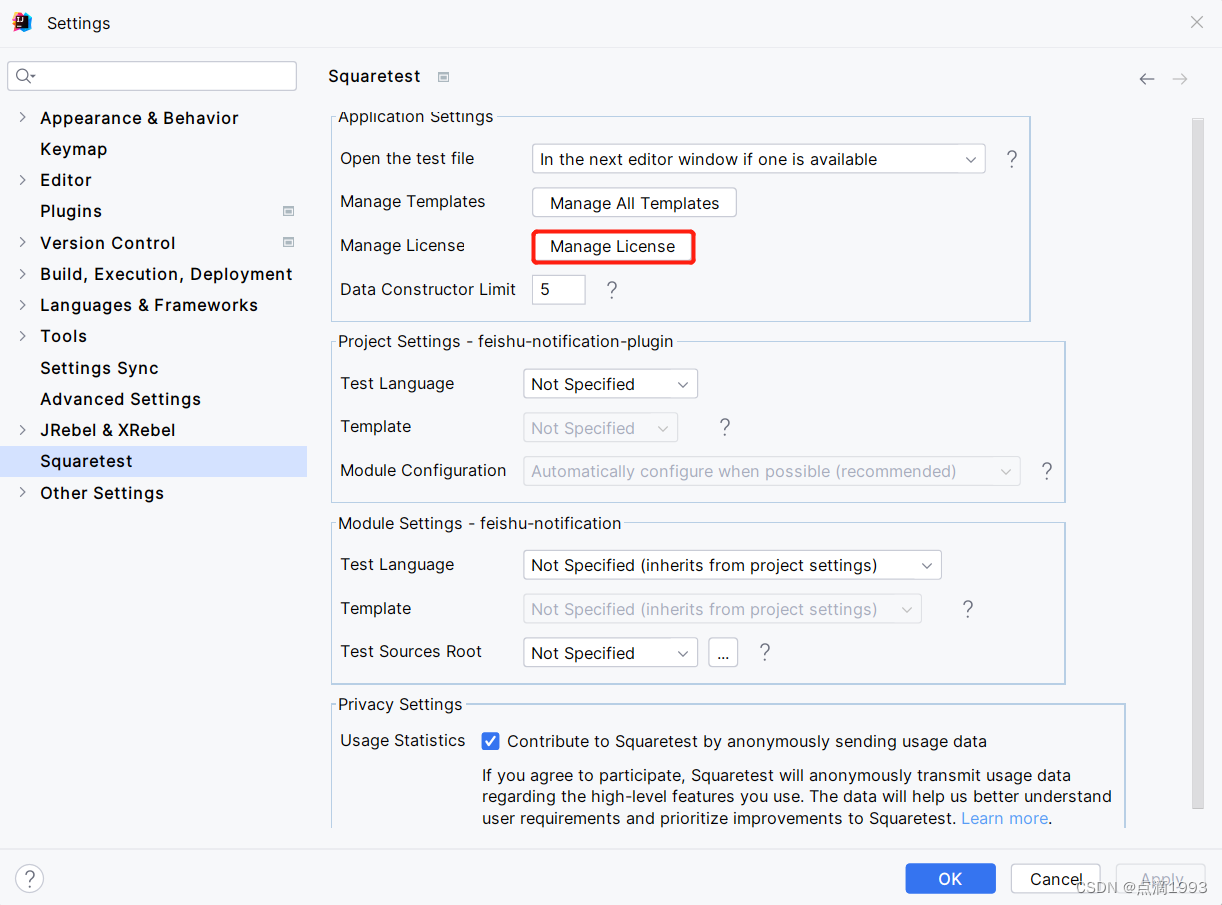
Squaretest 1.8.3 安装激活
1. 插件下载 2. 离线安装 3. 插件激活...

P21~22 第六章 储能元件——电容存储电场能,电感存储磁场能
1、电容元件 a定义 b线性时不变电容元件 c电容的电压与电流关系 i有限则u有限 注意理解面积 d电容的功率和储能 e例一 跃变就是指物体的物理量从有限值变为无限值的过程。 分析上图例题:对于电源波形要吃负无穷到正无穷去刻画。即时间轴要铺满。 有有图控制电…...
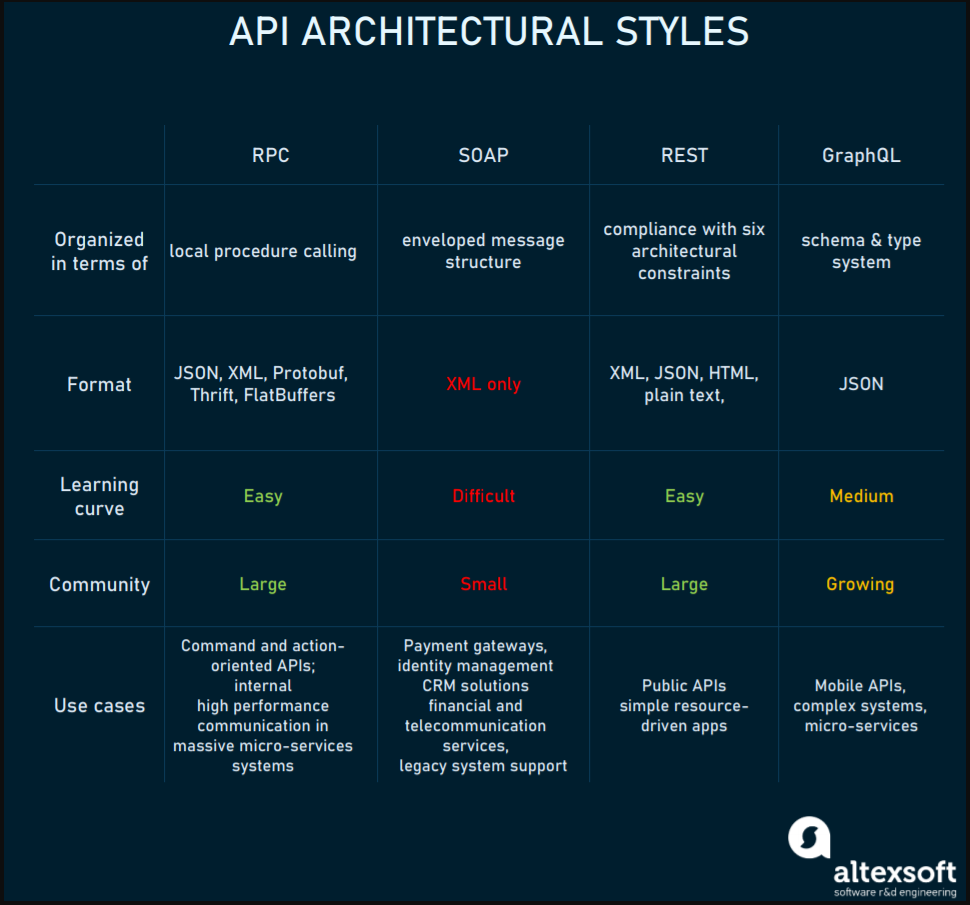
常见API架构介绍
常见API架构介绍 两个服务间进行接口调用,通过调用API的形式进行交互,这是常见CS架构实现的模式,客户端通过调用API即可使用服务端提供的服务。相较于SPI这种模式,就是服务端只规定服务接口,但具体实现交由第三方或者自…...
)
Vue全局组件与局部组件(详解)
当使用 Vue.js 构建应用时,组件是其核心概念之一。Vue 组件允许你将用户界面分割成独立、可复用的部分。这里我会更详细地解释 Vue 的全局组件和局部组件,包括它们的定义、使用方式以及适用场景。 Vue 全局组件: 全局组件是在整个 Vue 应用…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...
