数据结构,队列,顺序表队列,链表队列
队列是一种常见的数据结构,它具有先进先出(First-In-First-Out,FIFO)的特性,类似于排队等候的场景。以下是队列的要点:
1. 定义:队列是一种线性数据结构,由一系列元素组成,可以进行插入和删除操作。插入操作(称为入队)只能在队列的末尾进行,删除操作(称为出队)只能从队列的前端进行。
2. 特性:队列遵循先进先出的原则,最先入队的元素将最先出队。
3. 基本操作:
- 入队(Enqueue):将元素插入到队列的末尾。
- 出队(Dequeue):从队列的前端删除一个元素,并返回删除的元素。
- 队列是否为空(isEmpty):判断队列是否为空,即没有任何元素。
- 队列长度(size):返回队列中元素的个数。
4. 实现方式:
- 数组:使用数组实现队列时,需要维护两个指针,一个指向队列的前端,另一个指向队列的末尾。出队时移动前端指针,入队时移动末尾指针。注意需要循环利用数组空间。
- 链表:使用链表实现队列时,新元素可以直接添加到链表末尾,出队时删除链表的头节点。
5. 队列的应用:
- 广度优先搜索算法(BFS):在图的遍历中,广度优先搜索需要使用队列来实现层次遍历。
- 计算机任务调度:操作系统中的任务调度可以使用队列来管理任务的执行顺序。
- 队列作为其他数据结构的辅助结构:例如,树的层次遍历、图的广度优先搜索等。
6. 常见类型:
- 普通队列(普通队列):遵循FIFO原则,用于常规的数据排队。
- 优先队列(Priority Queue):在出队时按照优先级进行排序,元素的出队顺序不一定按照插入顺序。
队列在计算机科学中具有广泛的应用,从操作系统到算法设计都有着重要作用。它是解决许多问题的重要工具之一。
顺序表队列
/*===============================================
* 文件名称:queue.c
* 创 建 者:WM
* 创建日期:2023年08月21日
* 描 述:顺序队列//下标为rear里没有数据
================================================*/
#include <stdio.h>
#include<stdlib.h>
#define SIZE 8
typedef int data_t;//构造节点类型
typedef struct node{data_t data[SIZE];//保存数据的数据域data_t front;data_t rear;
} sequeue;
sequeue *createEmptySequeue()
{sequeue *p = (sequeue *)malloc(sizeof(sequeue));if(NULL == p){perror("createEmptySequeue malloc failed");return NULL;}//只要你申请空间就是为了让他装上数据p->rear = 0;//使用的时候是数组的下标p->front = 0;//使用的时候是数组的下标return p;
}
int insert(sequeue* sq,data_t h)
{sq->data[sq->rear]=h;sq->rear=(sq->rear+1)%SIZE;//注意
}
int out_queue(sequeue *sq)
{ data_t val=sq->data[sq->front];sq->front=(sq->front+1)%SIZE;printf("%d \n",val);return val;
}
int isQueue_empty(sequeue *sq)
{if(sq==NULL) -1;return sq->front==sq->rear;
}
//注意
int isQueue_full(sequeue *sq)
{//return (sq->rear-sq->front+SIZE)%SIZE==SIZE-1;//这个算法很重要return (sq->rear+1) % SIZE == sq->front;//或者这个。
}
//注意
int isQueue_full2(sequeue*sq)
{if(sq->front>sq->rear)return sq->front-sq->rear==1;if(sq->front<sq->rear)return sq->rear-sq->front==SIZE-1;
}int queue_num(sequeue* sq)//谁大谁在前面。
{return (sq->front<=sq->rear)?(sq->rear-sq->front):(sq->rear-sq->front+SIZE);
}void clear_queue(sequeue *sq)
{while (!isQueue_empty(sq))out_queue(sq);
}int main(int argc, char *argv[])
{ sequeue*phead=createEmptySequeue();for (int i = 0; i < SIZE-1; i++){insert(phead,i+1);}out_queue(phead);printf("%d \n",queue_num(phead));return 0;
}
链表队列
/*===============================================
* 文件名称:queue.c
* 创 建 者:WM
* 创建日期:2023年08月21日
* 描 述:链表队列
================================================*/
#include <stdio.h>
#include<stdlib.h>
typedef int data_t;//构造链表节点类型
typedef struct node{data_t data;//保存数据的数据域struct node*next;//保存下一个节点的地址
} linklist ;
typedef struct {linklist *front;linklist* rear;
} lqueue;lqueue* creat_lqueue()
{lqueue*lq=(lqueue*)malloc(sizeof(lqueue));lq->front=(linklist*)malloc(sizeof(linklist));lq->front->next=NULL;lq->rear=lq->front;return lq;
}
int insert(lqueue* lq,data_t h)
{linklist *new=(linklist *)malloc(sizeof(linklist));if(NULL==new) return -1;new->data=h;new->next=NULL;lq->rear->next=new;lq->rear=new;
}
int out_queue(lqueue*lq)
{linklist* m=lq->front->next;lq->front->next=m->next;int val=m->data;free(m);m=NULL;printf("%d \n",val);return val;
}
int isQueue_empty(lqueue*lq)
{return lq->front==lq->rear;
}
int queue_num(lqueue*lq)
{int len=0;linklist* h = lq->front;while (h->next!=NULL){h=h->next;len++;}return len;
}
void clear_queue(lqueue*lq)
{while (!isQueue_empty(lq))out_queue(lq);
}
int main(int argc, char *argv[])
{ lqueue*lqhead=creat_lqueue();insert(lqhead,9);insert(lqhead,110);printf("%d \n",queue_num(lqhead));out_queue(lqhead);out_queue(lqhead);printf("%d \n",queue_num(lqhead));clear_queue(lqhead);printf("%d \n",queue_num(lqhead));return 0;
}
相关文章:

数据结构,队列,顺序表队列,链表队列
队列是一种常见的数据结构,它具有先进先出(First-In-First-Out,FIFO)的特性,类似于排队等候的场景。以下是队列的要点: 1. 定义:队列是一种线性数据结构,由一系列元素组成ÿ…...
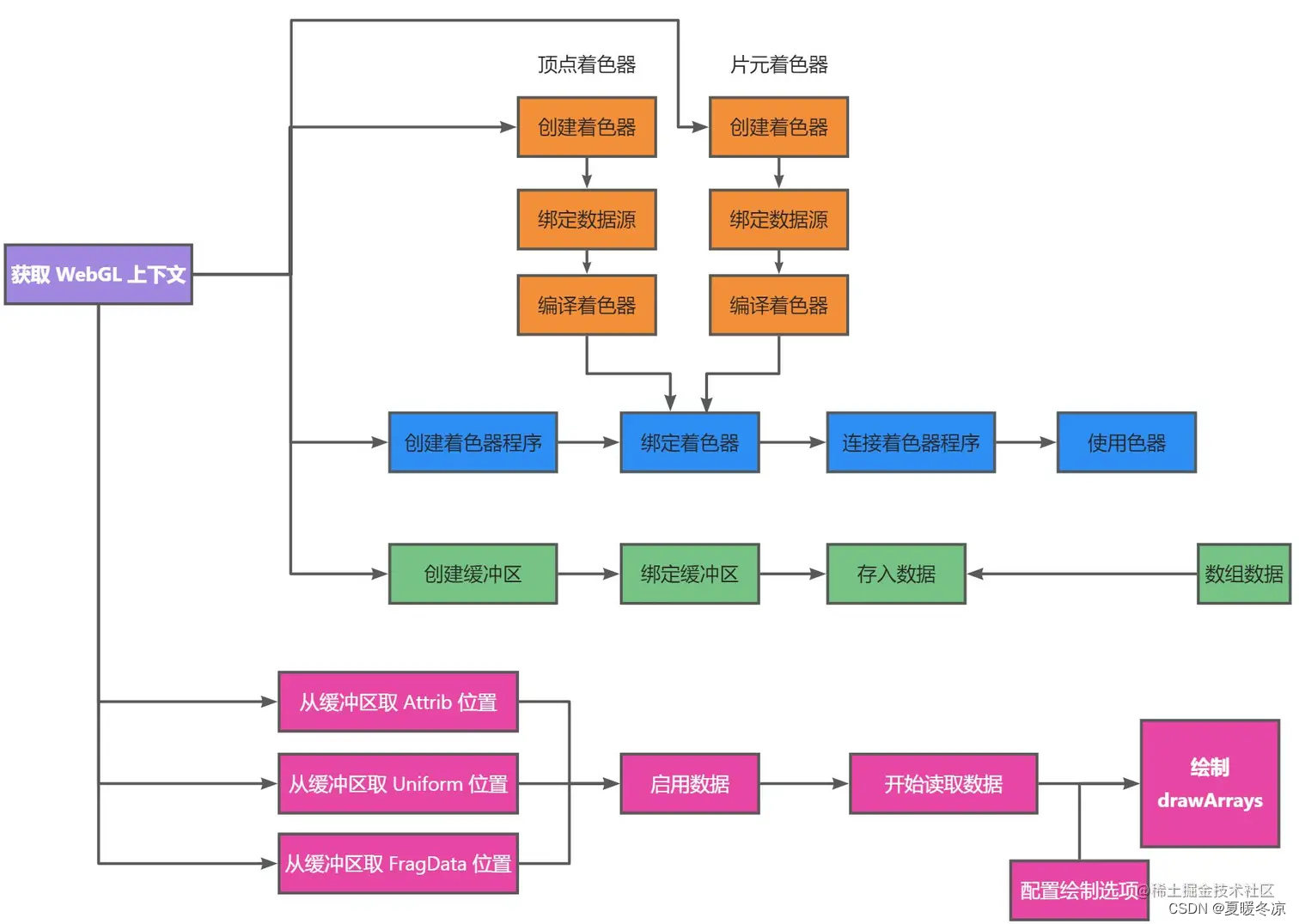
Webgl利用缓冲区绘制三角形
什么是attribute 变量 它是一种存储限定符,表示定义一个attribute的全局变量,这种变量的数据将由外部向顶点着色器内传输,并保存顶点相关的数据,只有顶点着色器才能使用它 <!DOCTYPE html> <html lang"en"&g…...

正则表达式应用
正则表达式应用 正则匹配以{开头,以}结尾 \{.*?\}正则匹配以[开头,以]结尾 \[.*?\]校验数字的表达式 数字:^[0-9]*$n位的数字:^\d{n}$至少n位的数字:^\d{n,}$m-n位的数字:^\d{m,n}$零和非零开头的数字…...

9.4 【C语言】用指针处理链表
9.4.1 什么是链表 它是动态地进行存储分配的一种结构。 链表中各元素在内存中的地址是不连续的。要找某一元素,必须先找到上一个元素,根据它提供的下一元素地址才能找到下一个元素。 如果不提供“头指针”,则整个链表无法访问。 9.4.2 建…...

后端面试话术集锦第四篇:rabbitmq面试话术
🚗后端面试集锦目录 💖后端面试话术集锦第一篇:spring面试话术💖 💖后端面试话术集锦第二篇:spring boot面试话术💖 💖后端面试话术集锦第三篇:spring cloud面试话术💖 💖后端面试话术集锦第四篇:ElasticSearch面试话术💖 💖后端面试话术集锦第五篇:r…...
 (三))
Linux目录结构与文件管理(01) (三)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、Linux 系统的组成 二、目录结构 根目录 三、文件管理 目录管理 总结 前言 今天主要学习了Linux的目录结构,主要是一些命令的含义和用法&am…...
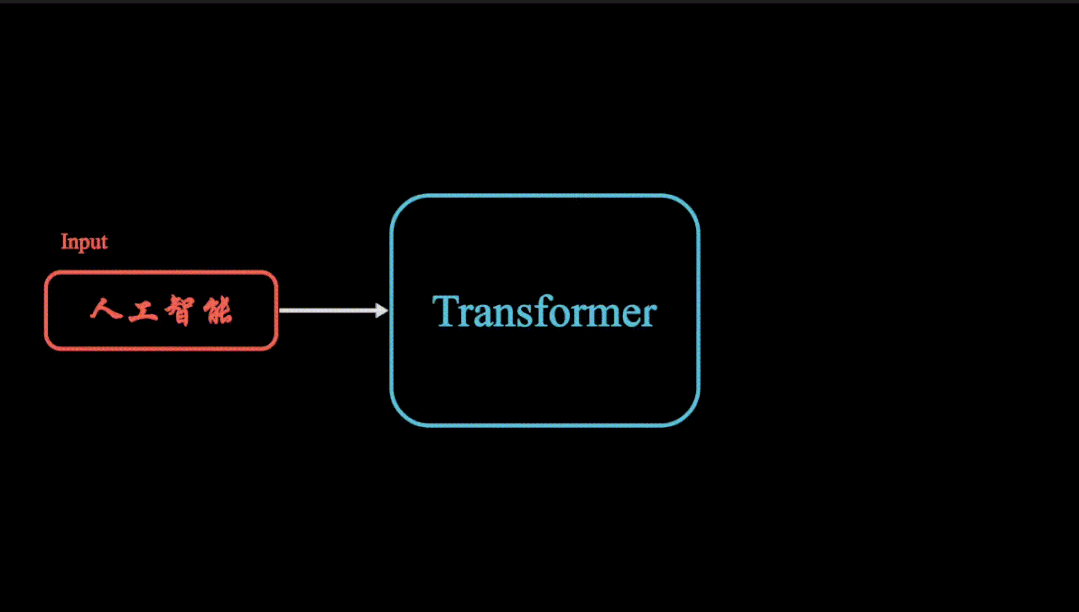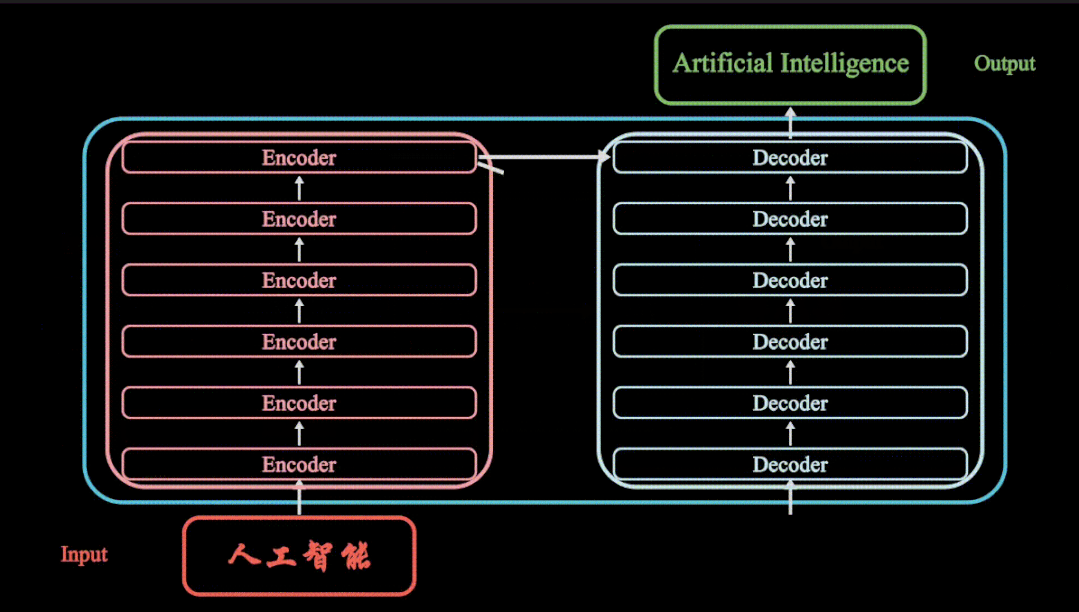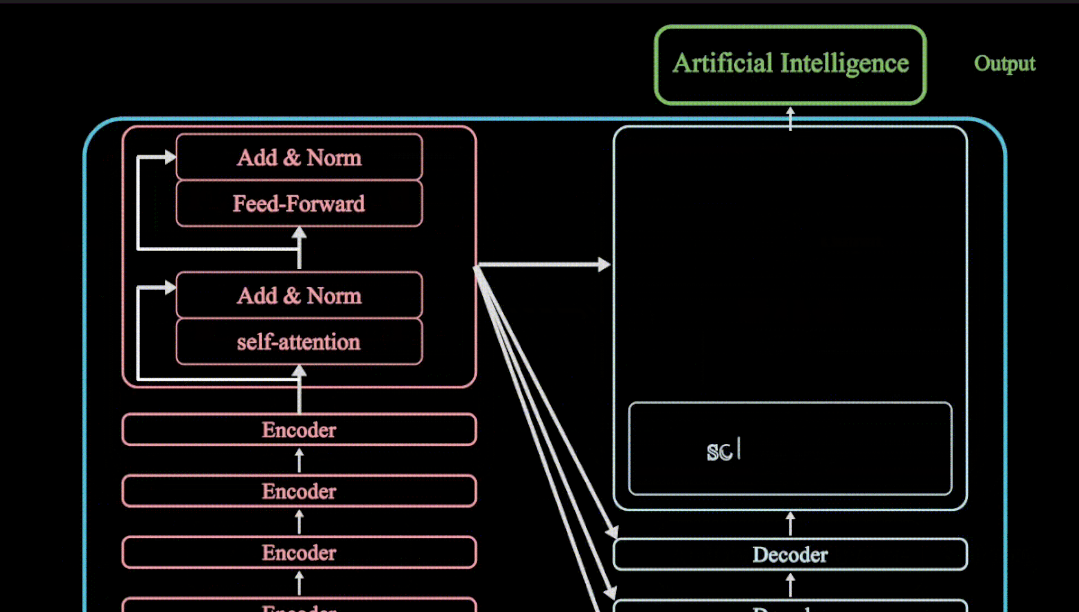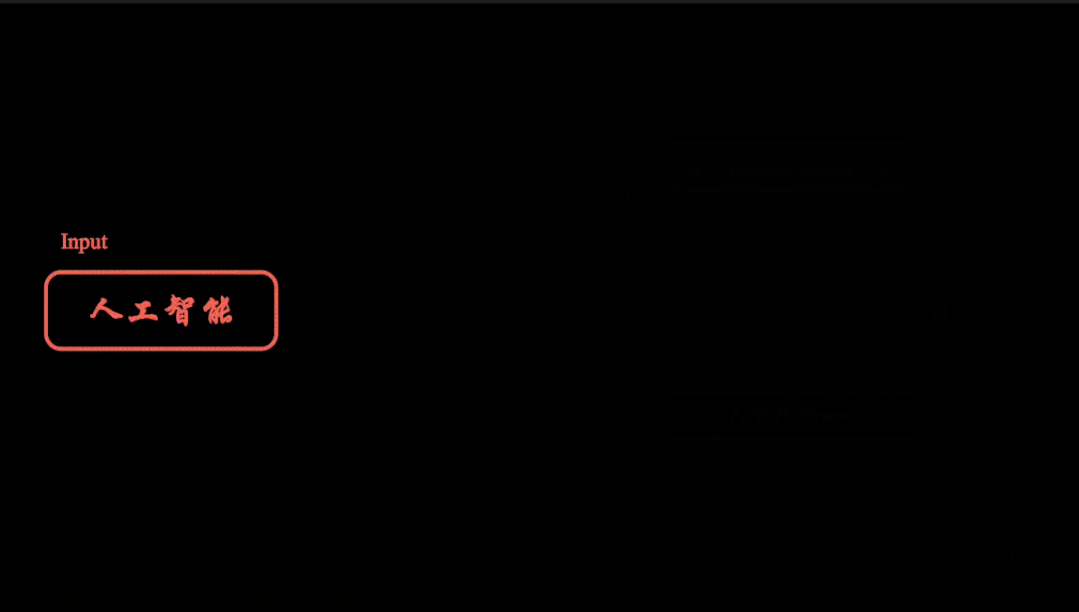
OpenCV为老照片,黑白照片增加色彩
Colorful Image Colorization 图片的颜色上色,主要使用到了CNN卷积神经网络,作者在ImageNet数据集上进行了大量的训练,并将此问题使用在分类任务中,以解决问题的潜在的不确定性,并在训练时使用颜色重新平衡的损失函数方…...
HTML之VSCode简单配置与创建
目录 插件下载 然后输入源码: 使用 效果 插件下载 下载这个插件后可以直接运行: 然后创建一个文件: 然后输入源码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"…...

2023亿发一体化新零售POS收银解决方案,打造连锁门店经营新未来
在零售业不断演变的今天,门店形态繁多,收银环节的共通性与差异性并存。传统的通用解决方案已不适应多样化的业态需求,而在线上线下一体化的时代背景下,全渠道经营能力也成为商家的迫切需求。 一体化新零售POS收银系统,…...
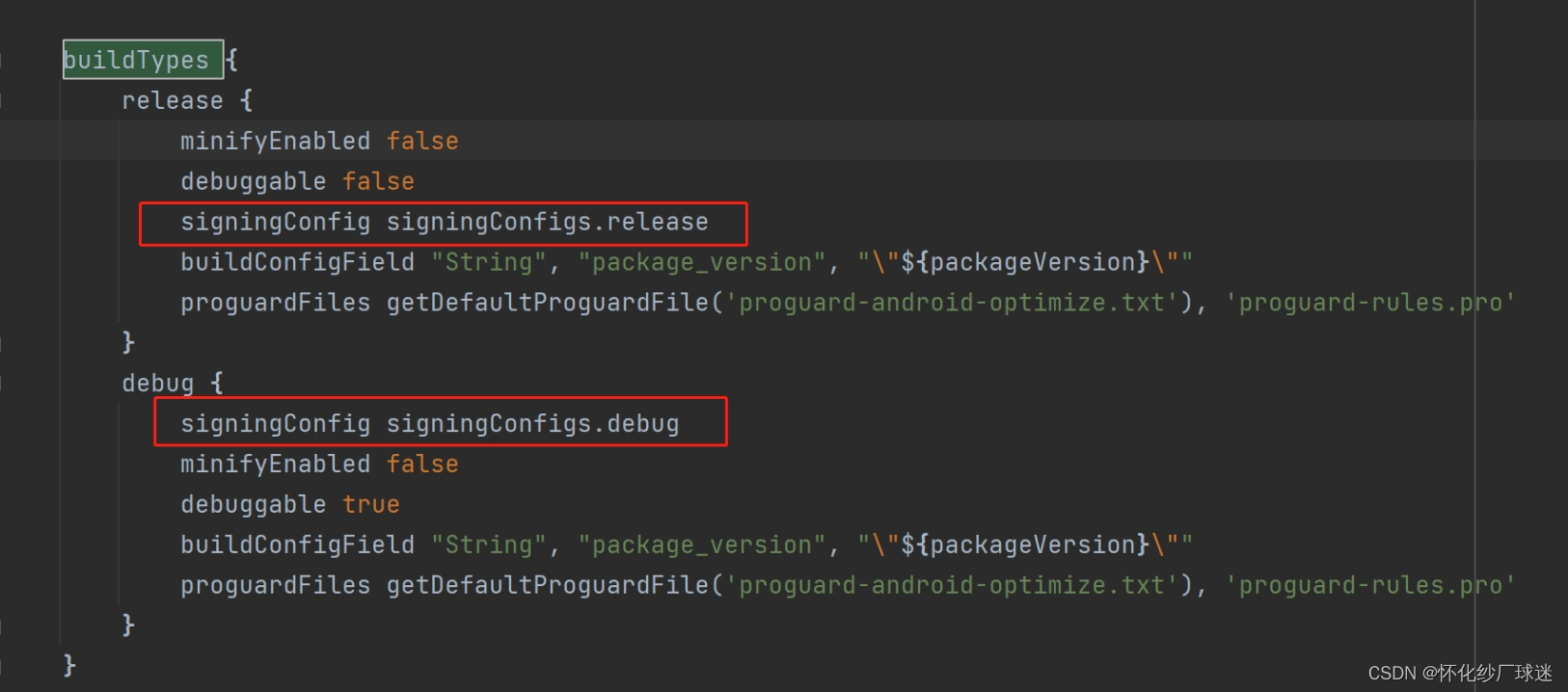
Android ---使用Jenkins 打包release版本不能安装或者安装后不显示APP
大家在用 Jenkins的时候,是不是会觉得很爽,因为他在用的过程中,是无脑的,毕竟一键触发!!!! 这边记录一个昨天,今天遇到的一个坑货问题,别人提交了所有代码&am…...

【Spring】什么是 AOP(面向切面编程) ? 为什么要有 AOP ? 如何实现 Spring AOP ?
文章目录 前言一、什么是 AOP ?二、为什么要使用 AOP ?三、 AOP 的组成四、Spring AOP 的实现1, 添加依赖2, 定义切面3, 定义切点4, 定义通知5, 创建连接点 总结 前言 各位读者好, 我是小陈, 这是我的个人主页, 希望我的专栏能够帮助到你: 📕 JavaSE基础: 基础语法…...

11.并发:自旋锁
原子操作和自旋锁的区别 相同点都是保护共享资源。 不同点在于: 原子操作简单易用,但只能做计数操作,保护的东西太少。 自旋锁主要用于多核处理器。短时期的轻量级加锁,加锁失败时原地打转、忙等待。避免了上下文调度和系统开销较…...

使用EF Core更新与修改生产数据库
使用EF Core的Code First,在设计阶段,直接使用Database.EnsureCreated()和EnsureDeleted()可以快速删除、更新最新的数据结构。由于没有什么数据,删除的风险非常低。但是对于已经投入生产的数据库,这个方法就绝对不可行了。 考虑…...
法律小程序开发:让法律咨询更便捷
在现代社会,法律咨询服务越来越受到人们的重视和需求。为了方便用户预约法律咨询,很多律所都开始使用小程序来提供在线预约服务。那么,如何制作一款律所预约小程序呢? 首先,我们可以选择乔拓云网作为制作小程序的平台。…...

【C++多线程】C++11互斥锁和条件变量实现生产者消费者模型
先看几个问题,第三个问题可以先看代码然后再理解 Q1:临界区在哪 A1: 队列中元素在「生产者生产(push)」和「消费者消费(pop)」时就是临界区 Q2:同步操作在哪 A2: 很显然,队列只有…...

Webpack迁移Vite采坑指南
前言 本文不介绍什么是webpack、什么是vite,也不分析为什么要迁移。如果你想从webpack迁移到vite,你可能会遇到一些坑,这里我会尽量详细地介绍每一种可能遇到的坑以及解决办法。 老规矩,先说AI的评价:这篇从webpack迁…...

设计模式-职责链模式
文章目录 职责链模式模式概述主要角色适用场景实现步骤优点注意事项 定义职责链结构示例总结 职责链模式 职责链模式是一种行为设计模式,它可以将请求的发送者和请求的处理者解耦,并按照预定义的顺序处理请求。职责链模式常用于需要逐级审批或转交处理的…...

CMake学习笔记-VSCode使用Cmake编译C++工程
环境 Win MinGW CMake Git 单文件工程 # 1 指定最小版本号 cmake_minimum_required(VERSION 3.10) # 2 指定工程名 project(Tutorial) # 3 设置编译器路径 set(CMAKE_C_COMPILER "D:/ProgramPackage/mingw64/mingw64/bin/gcc.exe") set(CMAKE_CXX_COMPILER &q…...

redis相关
如果redis没有设置expire,他是否默认永不过期? 清理线上Redis没有设置过期时间的key_青苔小榭的博客-CSDN博客 如何给Redis中未设置过期时间key添加过期时间? - 知乎 Redis中的几种更新策略_如何实现redis数据的局部更新_LG_985938339的博客…...
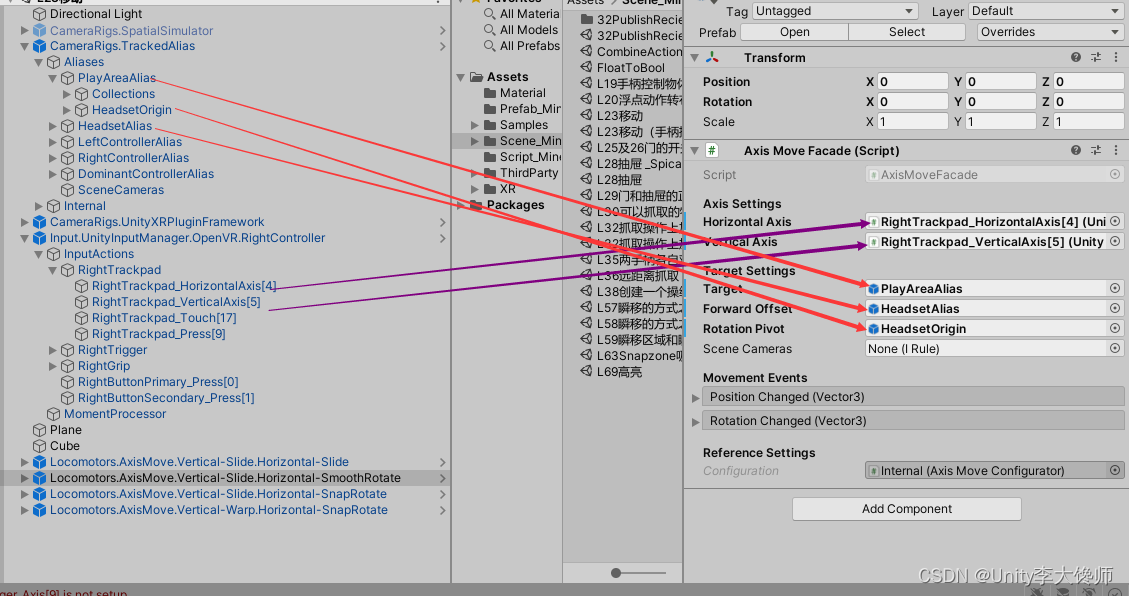
【VRTK4.0运动专题】轴移动AxisMove(真实身体的移动)
文章目录 1、概览2、释义3、属性设置 1、概览 2、释义 “竖直轴”控制的行为“水平轴”控制的行为1Vertical-Slide 滑动Horizontal-Slide 滑动2Vertical-Slide 滑动Horizontal-SmoothRotate 转动3Vertical-Slide 滑动Horizontal-SnapRotate 转动(不连续)…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...
