【考研数学】线形代数第三章——向量 | 3)向量组秩的性质、向量空间、过渡矩阵
文章目录
- 引言
- 三、向量组等价、向量组的极大线性无关组与秩
- 3.2 向量组秩的性质
- 四、 n n n 维向量空间
- 4.1 基本概念
- 4.2 基本性质
- 写在最后
引言
紧接前文学习完向量组秩的基本概念后,继续往后学习向量的内容。
三、向量组等价、向量组的极大线性无关组与秩
3.2 向量组秩的性质
性质 1(三秩相等) —— 设 A = ( β 1 , β 2 , … , β n ) = ( α 1 , α 2 , … , α n ) T \pmb{A=(\beta_1,\beta_2,\dots,\beta_n)=(\alpha_1,\alpha_2,\dots,\alpha_n)^T} A=(β1,β2,…,βn)=(α1,α2,…,αn)T ,其中 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 与 β 1 , β 2 , … , β n \pmb{\beta_1,\beta_2,\dots,\beta_n} β1,β2,…,βn 分别为矩阵 A A A 的行向量组和列向量组,则矩阵 A A A 的秩、 A A A 的行向量组的秩、 A A A 的列向量组的秩相等。
性质 2 —— 设 A : α 1 , α 2 , … , α n A:\pmb{\alpha_1,\alpha_2,\dots,\alpha_n} A:α1,α2,…,αn 与 B : β 1 , β 2 , … , β n B:\pmb{\beta_1,\beta_2,\dots,\beta_n} B:β1,β2,…,βn 为两个维数相同的向量组,若向量组 A A A 可由向量组 B B B 线性表示,则向量组 A A A 的秩不超过向量组 B B B 的秩。
性质 3 —— 等价的向量组秩相等,反之不对。
1,设向量组 A : α 1 , α 2 , … , α n A:\pmb{\alpha_1,\alpha_2,\dots,\alpha_n} A:α1,α2,…,αn 与 B : β 1 , β 2 , … , β n B:\pmb{\beta_1,\beta_2,\dots,\beta_n} B:β1,β2,…,βn 的秩相等,且向量组 A A A 可由向量组 B B B 线性表示,则向量组 A A A 与向量组 B B B 等价。
2,设向量组 A : α 1 , α 2 , … , α n A:\pmb{\alpha_1,\alpha_2,\dots,\alpha_n} A:α1,α2,…,αn 可由 B : β 1 , β 2 , … , β n B:\pmb{\beta_1,\beta_2,\dots,\beta_n} B:β1,β2,…,βn 线性表示,但向量组 A A A 不可由向量组 B B B 线性表示,则向量组 A A A 的秩小于向量组 B B B 。
3,两个等价的向量组,各自构成的矩阵也等价,但反之不一定。
四、 n n n 维向量空间
4.1 基本概念
n n n 维向量空间 —— 所有 n n n 维向量连同向量的加法及数与向量的乘法运算称为 n n n 维向量空间,记为 R n . \pmb{R}^n. Rn.
基 —— 设 R n \pmb{R}^n Rn 为 n n n 维向量空间,设 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 为向量空间中的 n n n 个向量,若满足:
(1) α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性无关;
(2)对任意的 β ∈ R n , β \pmb{\beta \in R^n,\beta} β∈Rn,β 都可由向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性表示,
称 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 为 n n n 维向量空间 R n R^n Rn 的基。
特别地,若 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 两两正交,且都是单位向量,称其为正交规范基。
向量在基下的坐标 —— 设 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 为 R n R^n Rn 的基, β ∈ R n \beta \in R^n β∈Rn ,若 β = k 1 α 1 + k 2 α 2 + ⋯ + k n α n \beta=k_1\alpha_1+k_2\alpha_2+\dots+k_n\alpha_n β=k1α1+k2α2+⋯+knαn ,称 ( k 1 , k 2 , … , k n ) (k_1,k_2,\dots,k_n) (k1,k2,…,kn) 为向量 β \beta β 在基 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 下的坐标。
过渡矩阵 —— 由一组基变换为另一组基,可乘上一个矩阵,该矩阵称为过渡矩阵。
需要一些直观印象,才能更好理解向量空间。首先应理解的是,一个矩阵就代表一种变换。
4.2 基本性质
定理 1 设 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 为 n n n 维向量空间 R n R^n Rn 的基, β ∈ R n \beta \in R^n β∈Rn ,令 A = ( α 1 , α 2 , … , α n ) A=(\pmb{\alpha_1,\alpha_2,\dots,\alpha_n}) A=(α1,α2,…,αn) ,则向量 β \beta β 在基 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 下的坐标为 X = A − 1 β . \pmb{X=A^{-1}\beta}. X=A−1β.
定理 2 —— 设 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 与 β 1 , β 2 , … , β n \pmb{\beta_1,\beta_2,\dots,\beta_n} β1,β2,…,βn 为向量空间 R n R^n Rn 的两个基,令 A = ( α 1 , α 2 , … , α n ) , B = ( β 1 , β 2 , … , β n ) A=(\pmb{\alpha_1,\alpha_2,\dots,\alpha_n}),B=(\pmb{\beta_1,\beta_2,\dots,\beta_n}) A=(α1,α2,…,αn),B=(β1,β2,…,βn) ,则从基 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 到基 β 1 , β 2 , … , β n \pmb{\beta_1,\beta_2,\dots,\beta_n} β1,β2,…,βn 的过渡矩阵为 Q = A − 1 B . \pmb{Q=A^{-1}B}. Q=A−1B.
定理 3 —— 从基 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 到基 β 1 , β 2 , … , β n \pmb{\beta_1,\beta_2,\dots,\beta_n} β1,β2,…,βn 的过渡矩阵与从基 β 1 , β 2 , … , β n \pmb{\beta_1,\beta_2,\dots,\beta_n} β1,β2,…,βn 到基 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 到的过渡矩阵互为逆矩阵。
写在最后
到此,向量的理论部分就结束了。矩阵、向量、方程组三者的联系最近会总结发出来的。
相关文章:
向量组秩的性质、向量空间、过渡矩阵)
【考研数学】线形代数第三章——向量 | 3)向量组秩的性质、向量空间、过渡矩阵
文章目录 引言三、向量组等价、向量组的极大线性无关组与秩3.2 向量组秩的性质 四、 n n n 维向量空间4.1 基本概念4.2 基本性质 写在最后 引言 紧接前文学习完向量组秩的基本概念后,继续往后学习向量的内容。 三、向量组等价、向量组的极大线性无关组与秩 3.2 向…...
【技术】SpringBoot Word 模板替换
SpringBoot Word 模板替换 什么是 Word 模板替换如何实现 Word 模板替换 什么是 Word 模板替换 模板一般是具有固定格式的内容,其中一部分需要替换。Word 模板通俗的讲是以 Word 的形式制作模板,固定格式和内容,然后将其中的一部分数据替换掉…...

java jni nv21和nv12互转
目录 libyuv性能比较 NV12 NV21 YUV420格式介绍 jni YUV420toYUV420SemiPlanar java YUV420toYUV420SemiPlanar java NV12toYUV420SemiPlanar jni NV12toYUV420SemiPlanar...

后端面试话术集锦第二篇:spring boot面试话术
🚗后端面试集锦目录 💖后端面试话术集锦第一篇:spring面试话术💖 💖后端面试话术集锦第二篇:spring boot面试话术💖 💖后端面试话术集锦第三篇:spring cloud面试话术💖 💖后端面试话术集锦第四篇:ElasticSearch面试话术💖 💖后端面试话术集锦第五篇:r…...

Doris中分区和分桶使用教程
1 分区与分桶 Doris中有两层的数据划分,第一层是分区(Partition),第二层是分桶(Bucket), Partition又能分为Range分区和List分区。 Bucket仅支持Hash方式。 1.1 Partition 只能指定…...
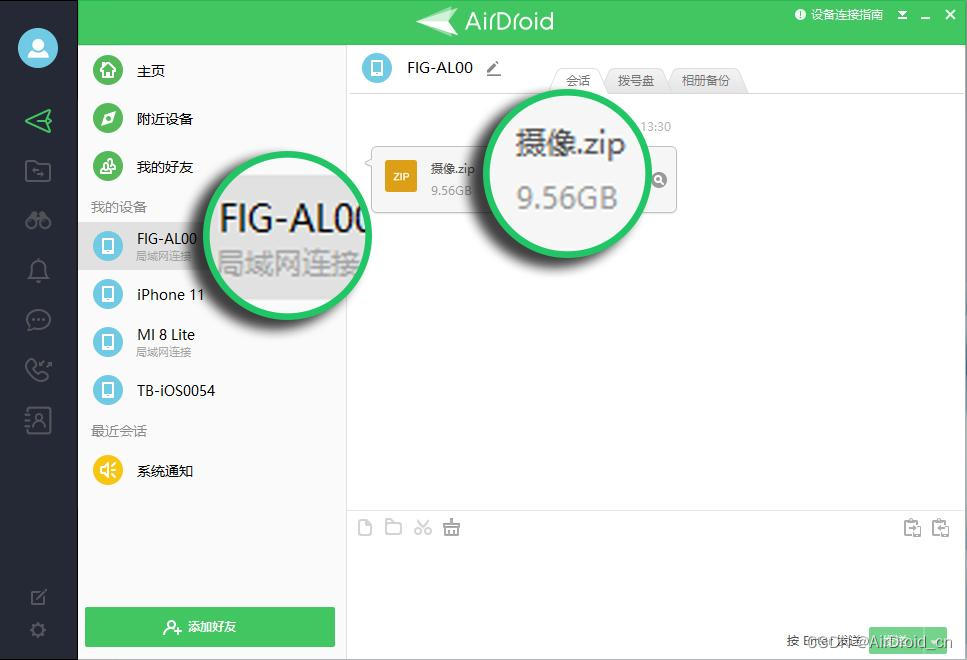
电脑不安装软件,怎么将手机文件传输到电脑?
很多人都知道,AirDroid有网页版(web.airdroid.com)。 想要文件传输,却不想在电脑安装软件时,AirDroid的网页版其实也可以传输文件。 然而,要将文件从手机传输文件到网页端所在的电脑时,如果按…...

vue3 publish 出现的问题
vue3项目使用 yarn build 编译出dist文件, 发布后出现错误 #问题与解决 1)登录迭代错误(Maximum call stack size exceeded) >deepclone 的问题 在 GrandhallLayout 中判断菜单和权限中; const mainMenu cloneDeep(router.getRoutes()) lodash.clonedee…...

网络防御和入侵检测
网络防御和入侵检测是维护网络安全的关键任务,可以帮助识别和阻止未经授权的访问和恶意行为。以下是一些基本的步骤和方法,用于进行网络防御和入侵检测。 网络防御: 防火墙设置: 部署防火墙来监控和控制网络流量,阻止…...
【科研论文配图绘制】task5 SciencePlots绘图包入门
【科研论文配图绘制】task5 SciencePlots绘图包入门 task5主要学习了SciencePlots拓展包的出图样式,掌握SciencePlots的安装及具体使用。 SciencePlots作为一个专门用于科研论文绘图的第三方拓展工具包,提供了主流英文科技 期刊(如 Nature、Science 和 …...

R语言常用数学函数
目录 1. - * / ^ 2.%/%和%% 3.ceiling,floor,round 4.signif,trunc,zapsamll 5.max,min,mean,pmax,pmin 6.range和sum 7.prod 8.cumsum,cumprod,cummax,cummin 9.sort 10. approx 11.approx fun 12.diff 13.sign 14.var和sd 15.median 16.IQR 17.ave 18.five…...
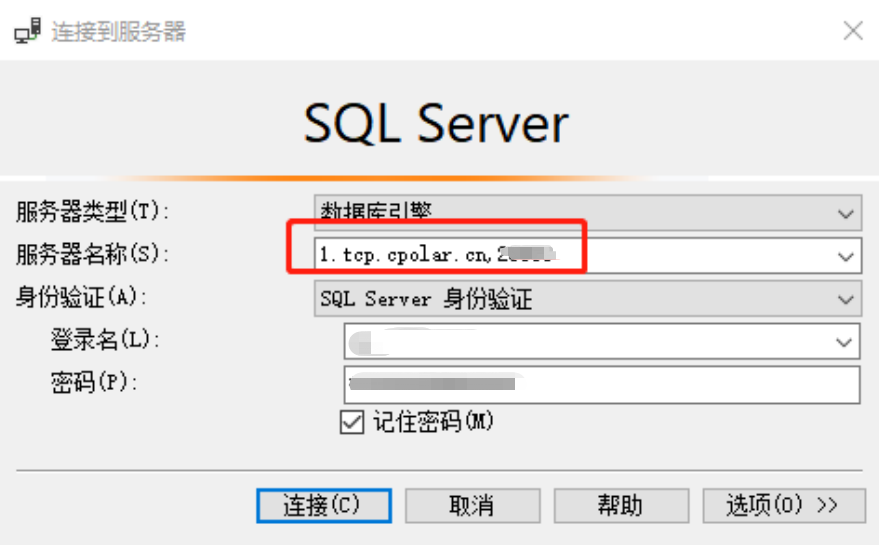
公网远程访问局域网SQL Server数据库
文章目录 1.前言2.本地安装和设置SQL Server2.1 SQL Server下载2.2 SQL Server本地连接测试2.3 Cpolar内网穿透的下载和安装2.3 Cpolar内网穿透的注册 3.本地网页发布3.1 Cpolar云端设置3.2 Cpolar本地设置 4.公网访问测试5.结语 1.前言 数据库的重要性相信大家都有所了解&…...

Apache Celeborn 让 Spark 和 Flink 更快更稳更弹性
摘要:本文整理自阿里云/数据湖 Spark 引擎负责人周克勇(一锤)在 Streaming Lakehouse Meetup 的分享。内容主要分为五个部分: Apache Celeborn 的背景Apache Celeborn——快Apache Celeborn——稳Apache Celeborn——弹Evaluation…...
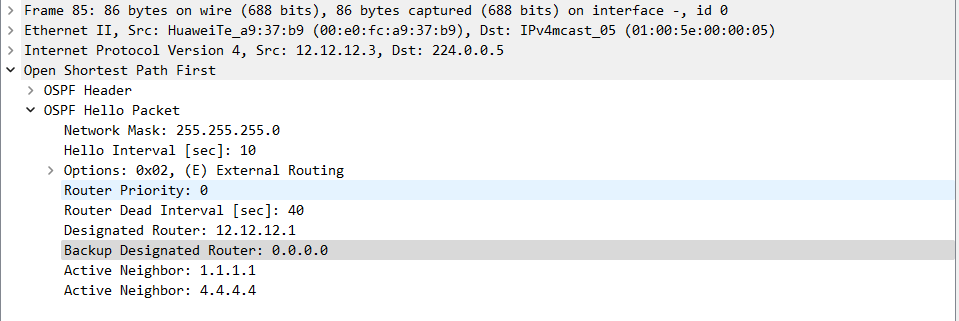
华为数通方向HCIP-DataCom H12-821题库(单选题:141-160)
第141题 Router-LSA 能够描述不同的链路类型,不属于Router LSA 链路类型的是以下哪一项? A、Link Type 可以用来描述到末梢网络的连接,即 SubNet B、Link Type 可以用来描述到中转网络的连接,即 TranNet C、Link Type 可以用来描述到另一…...

Windows-docker集成SRS服务器的部署和使用
Windows-docker集成SRS服务器的部署和使用 一、Windows Docker安装 Docker Desktop 官方下载地址: https://docs.docker.com/desktop/install/windows-install/ 下载windows版本的就可以了。 注意:此方法仅适用于 Windows 10 操作系统专业版、企业版、…...

element-ui table表格滚动条拉到最右侧 表头与内容不能对齐
1.问题概述 当表格数据太多,会出现纵向滚动条和横向滚动条,把横向滚动条拉到最右侧时,会出现表头与内容不能对齐的现象。 2.解决方法 1.当页面数据加载完毕后,在后面加上 this.$nextTick(() > {this.$refs.table.doLayout()…...

React中的性能测试工具组件Profiler的基本使用
React中的性能测试工具组件Profiler是一个非常有用的工具,它可以帮助我们分析React应用程序的性能瓶颈。在本文中,我们将学习如何使用Profiler组件来测试React应用程序的性能。 首先,让我们来了解一下Profiler组件的基本用法。在React中&…...

提升生产效率,降低运维成本:纺织业物联网网关应用
在众多物联网技术应用中纺织业正逐渐崭露头角。物联网技术通过无线连接纺织设备、PLC、传感器,实现了纺织厂的生产数据信息的远程监控和数据采集、远程管理,为企业提供了更高效、智能的生产方式。智联物联小编在本文中将重点介绍纺织业物联网的应用与通讯…...
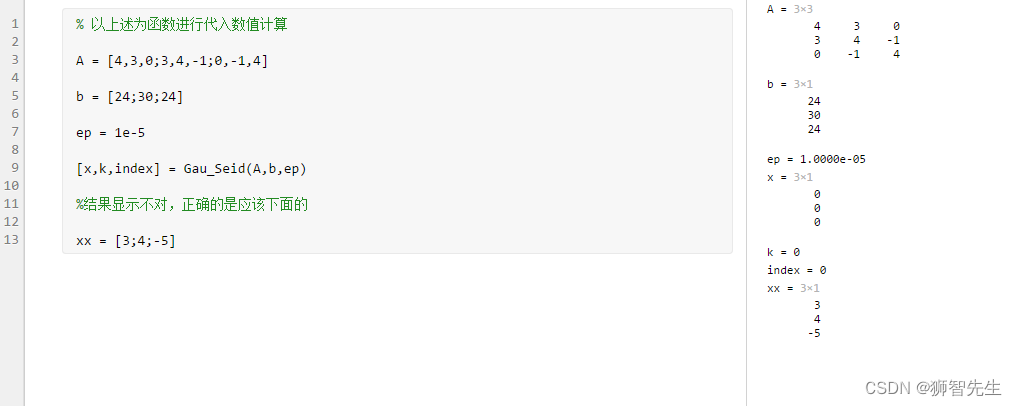
【学习笔记】求解线性方程组的G-S迭代法
求解线性方程组的G-S迭代法 // 运行不成功啊function [x,k,index] Gau_Seid(A,b,ep,it_max) % 求解线性方程组的G-S迭代法,其中 % A为方程组的系数矩阵 % b为方程组的右端项 % ep为精度要求,省缺为1e-5 % it_max为最大迭代次数,省缺为100 % …...
Kotlin协程flow缓冲buffer
Kotlin协程flow缓冲buffer 先看一个普通的flow: import kotlinx.coroutines.delay import kotlinx.coroutines.flow.* import kotlinx.coroutines.runBlocking import kotlin.system.measureTimeMillisfun main(args: Array<String>) {val delayTime 100Lru…...
完全免费的GPT,最新整理,2023年8月24日,已人工验证,不用注册,不用登录,更不用魔法,点开就能用
完全免费的ChatGPT,最新整理,2023年8月24日,已人工验证, 不用注册,不用登录,更不用魔法,点开就能用! 第一个:网址地址统一放在文末啦!文末直达 看上图你就能…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...
