R语言常用数组函数
目录
1.array
2.matrix
3.data.matrix
4.lower.tri
5.mat.or.vec
6.t:转置矩阵
7.cbind
8.rbind
9.diag
10.aperm:对数组进行轴置换(维度重排)操作
11.%*%:乘法操作要求矩阵 A 的列数等于矩阵 B 的行数
12.crossprod:用于计算矩阵的交叉积
13.outer
14.Kronecker
15. apply
16.tapply
17.sweep:对矩阵的某个维度进行操作
18.aggregate
19.scale
20.matplot
21.cor
22.Contrast,row,col
1.array
array(data, dim = NULL, dimnames = NULL)
data:填充数组的数据向量或矩阵。dim:指定数组的维度,即一个整数向量。例如,dim = c(3, 4, 2)表示创建一个3行、4列、2个深度(即三维)的数组。dimnames:指定数组维度的名称,通常是一个包含维度名称的列表。每个元素可以是字符向量,用于为相应维度的标签命名。
(1)创建一个二维数组
arr_2d <- array(data = c(1, 2, 3, 4), dim = c(2, 2))
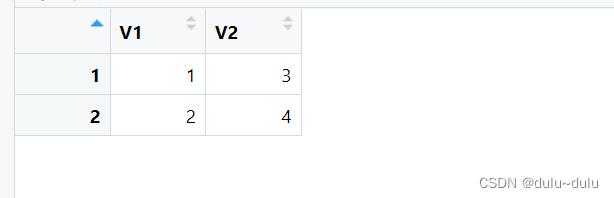
(2)创建一个三维数组
arr_3d <- array(data = c(1, 2, 3, 4, 5, 6), dim = c(2, 3, 1))
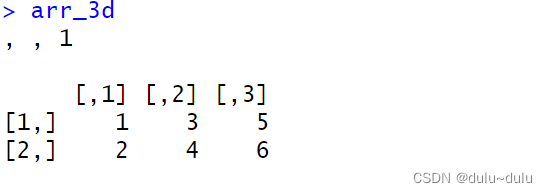
(3)创建一个具有维度名称的数组
arr_named <- array(data = c(1, 2, 3, 4), dim = c(2, 2), dimnames = list(c("row1", "row2"), c("col1", "col2")))

2.matrix
matrix(data, nrow = 1, ncol = 1, byrow = FALSE, dimnames = NULL)
data:用于填充矩阵的数据向量或矩阵。nrow:指定矩阵的行数。ncol:指定矩阵的列数。byrow:逻辑值,指定是否按行填充矩阵,默认为FALSE表示按列填充。dimnames:矩阵维度的名称。
# 创建一个2行3列的矩阵
mat <- matrix(data = c(1, 2, 3, 4, 5, 6), nrow = 2, ncol = 3)
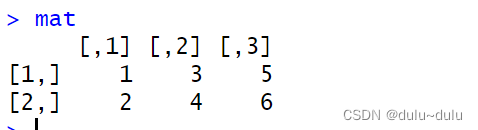
3.data.matrix
# 创建一个数据框
df <- data.frame(a = c(1, 2, 3),b = c(4, 5, 6),c = c(7, 8, 9))# 将数据框转换为数值型矩阵
mat <- data.matrix(df)# 打印输出结果
print(mat)

4.lower.tri
# 创建一个3x3的矩阵
mat <- matrix(c(1, 2, 3, 4, 5, 6, 7, 8, 9), nrow = 3)# 提取矩阵的下三角部分
lower_tri <- lower.tri(mat)# 打印输出结果
print(lower_tri)

5.mat.or.vec
# 生成一个2行3列的零矩阵
m <- mat.or.vec(nr = 2, nc = 3)# 生成一个含有5个元素的零向量
v <- mat.or.vec(nr = 5, nc = 1)
6.t:转置矩阵
# 创建一个3x2的矩阵
mat <- matrix(c(1, 2, 3, 4, 5, 6), nrow = 3)# 对矩阵进行转置
transposed_mat <- t(mat)# 打印输出结果
print(transposed_mat)

7.cbind
# 创建两个向量
v1 <- c(1, 2, 3)
v2 <- c(4, 5, 6)# 将两个向量按列合并
result <- cbind(v1, v2)# 打印输出结果
print(result)

8.rbind
# 创建两个向量
v1 <- c(1, 2, 3)
v2 <- c(4, 5, 6)# 将两个向量按行合并
result <- rbind(v1, v2)# 打印输出结果
print(result)

9.diag
获取对角矩阵元素
# 创建一个3x3的矩阵
mat <- matrix(c(1, 2, 3, 4, 5, 6, 7, 8, 9), nrow = 3)# 获取矩阵的对角元素向量
diag_vec <- diag(mat)# 打印输出结果
print(diag_vec)#输出 [1] 1 5 9
生成对角矩阵
# 创建一个5x5的对角矩阵,对角线上的元素为1
diag_mat <- diag(1, nrow = 5)# 打印输出结果
print(diag_mat)

10.aperm:对数组进行轴置换(维度重排)操作
# 创建一个3x4x2的三维数组
arr <- array(1:24, dim = c(3, 4, 2))第一个维度行数,第二个维度列数,第三个维度层数# 对数组进行轴置换,重新排列维度
permuted_arr <- aperm(arr, perm = c(3, 2, 1))
#将第一个元素排在最后,第二个元素排在中间,第三个元素排在第一个,即(2,4,3)# 打印输出结果
print(permuted_arr)

11.%*%:乘法操作要求矩阵 A 的列数等于矩阵 B 的行数
# 创建两个矩阵
A <- matrix(c(1, 2, 3, 4), nrow = 2, ncol = 2)
B <- matrix(c(5, 6, 7, 8), nrow = 2, ncol = 2)# 执行矩阵乘法
C <- A %*% B# 打印结果
print(C)
矩阵A
[,1] [,2]
[1,] 1 3
[2,] 2 4
矩阵B[,1] [,2]
[1,] 5 7
[2,] 6 8
矩阵乘法运算
c_11 = (1*5) + (3*6) = 5 + 18 = 23#A的第一行,B的第一列
c_12 = (1*7) + (3*8) = 7 + 24 = 31#A的第一行,B的第二列
c_21 = (2*5) + (4*6) = 10 + 24 = 34#A的第二行,B的第一列
c_22 = (2*7) + (4*8) = 14 + 32 = 46#A的第二行,B的第二列
矩阵C的值
[,1] [,2]
[1,] 23 31
[2,] 34 46
12.crossprod:用于计算矩阵的交叉积
# 创建向量
x <- c(1, 2, 3)
y <- c(4, 5, 6)# 计算向量的内积
result <- crossprod(x, y)# 打印结果
print(result)
[,1]
[1,] 32计算过程:
[1, 2, 3] * [4, 5, 6] = (1 * 4) + (2 * 5) + (3 * 6) = 4 + 10 + 18 = 32
# 创建矩阵
A <- matrix(c(1, 2, 3, 4), nrow = 2, ncol = 2)# 计算矩阵的交叉积
result <- crossprod(A)# 打印结果
print(result)
矩阵A
[,1] [,2]
[1,] 1 3
[2,] 2 4
转置后的矩阵A[,1] [,2]
[1,] 1 2
[2,] 3 4[,1] [,2]
[1,] 1*1 + 2*2 1*3 + 2*4
[2,] 3*1 + 4*2 3*3 + 4*4
[,1] [,2]
[1,] 5 11
[2,] 11 25
13.outer
# 创建向量
x <- c(1, 2, 3)# 计算向量元素之间的外积
result <- outer(x, x)# 打印结果
print(result)#矩阵中的第 i 行和第 j 列的元素是向量 x 中的第 i 个元素与第 j 个元素的乘积。
[,1] [,2] [,3]
[1,] 1*1 1*2 1*3
[2,] 2*1 2*2 2*3
[3,] 3*1 3*2 3*3
14.Kronecker
# 创建两个矩阵
A <- matrix(c(1, 2, 3, 4), nrow = 2)
B <- matrix(c(5, 6, 7, 8), nrow = 2)# 计算Kronecker积
result <- kronecker(A, B)# 打印结果
print(result)
[,1] [,2] [,3] [,4]
[1,] 1*5 1*6 2*5 2*6#第一列*第一列
[2,] 1*7 1*8 2*7 2*8#第一列*第二列
[3,] 3*5 3*6 4*5 4*6#第二列*第一列
[4,] 3*7 3*8 4*7 4*8#第二列*第二列
15. apply
apply(X, MARGIN, FUN)
X是要操作的矩阵或数组
MARGIN指定要应用函数的维度(1表示行,2表示列,其他值表示整个维度)
FUN是要应用的函数。
# 创建一个矩阵
X <- matrix(1:9, nrow = 3)# 对每一行求和
row_sums <- apply(X, 1, sum)
print(row_sums)# 对每一列取平均值
col_means <- apply(X, 2, mean)
print(col_means)# 对整个矩阵进行乘法运算
matrix_product <- apply(X, c(1, 2), function(x) x * 2)
print(matrix_product)
[1] 6 15 24
[1] 2 5 8
[,1] [,2] [,3]
[1,] 2 8 18
[2,] 4 10 20
[3,] 6 12 22
16.tapply
tapply(X, INDEX, FUN)
X是要操作的向量或矩阵
INDEX是一个或多个因子,用于指定分组依据
FUN是要应用的函数。
# 创建一个向量
x <- c(1, 2, 3, 4, 5, 6)# 定义一个因子,用于分组
group <- c("A", "B", "A", "B", "A", "B")# 对向量按照因子进行分组,并对每个组求和
result <- tapply(x, group, sum)
print(result)
A B
9 12
17.sweep:对矩阵的某个维度进行操作
sweep(x, MARGIN, STATS, FUN = "-", ...)
x是要进行操作的矩阵
MARGIN指定要操作的维度(1为行,2为列)
STATS是要进行操作的向量或矩阵;FUN是要应用的函数,它将用于在矩阵的指定维度上进行操作,默认为减法(-)。
# 创建一个矩阵
x <- matrix(1:6, nrow = 2)# 创建一个要进行操作的向量
stats <- c(3, 2)# 对矩阵的每一列进行减法操作
result <- sweep(x, 2, stats, FUN = "-")
print(result)
每个元素-2
[,1] [,2]
[1,] -2 -1
[2,] -1 0
18.aggregate
aggregate(formula, data, FUN, ...)
formula是一个公式,指定了要汇总的变量和分组因子
data是包含要汇总的数据的数据框
FUN是要应用的函数
sum(): 求和mean(): 平均值median(): 中位数min(): 最小值max(): 最大值length(): 长度(计数)
# 创建一个数据框
df <- data.frame(group = c("A", "A", "B", "B", "A", "B"),value = c(1, 2, 3, 4, 5, 6)
)# 对数据框按照 group 列进行分组,并对每个组计算平均值
result <- aggregate(value ~ group, data = df, FUN = mean)
print(result)
group value
1 A 2.666667
2 B 4.333333
19.scale
scaled_data <- scale(x, center = TRUE, scale = TRUE)
x是要进行标准化处理的向量、矩阵或数据框;
center参数用于指定是否进行中心化,默认为TRUE,表示进行中心化;
scale参数用于指定是否进行缩放,默认为TRUE,表示进行缩放。
# 创建一个矩阵
x <- matrix(c(1, 2, 3, 4, 5, 6), nrow = 3)# 对矩阵按列进行标准化处理
scaled_data <- scale(x, center = TRUE, scale = TRUE)
print(scaled_data)
#通过标准化处理,每列的均值被转换成了 0,标准差变成了 1
#第一列的标准化结果是
[-1.2247449, 0.0000000, 1.2247449]#第二列的标准化结果也是
[-1.2247449, 0.0000000, 1.2247449]。[,1] [,2]
[1,] -1.2247449 -1.2247449
[2,] 0.0000000 0.0000000
[3,] 1.2247449 1.2247449
20.matplot
matplot(x, y = NULL, type = "l", lty = 1, lwd = 1, col = 1, pch = NULL, ...)
x是一个矩阵或数据框,它的每列(或每行)代表一个变量;
y是一个可选参数,当x为单个矩阵时,y可以为 NULL,当x为两个矩阵时,y表示第二个矩阵;
type参数指定绘图类型,可以是 "l"(线图)或 "p"(点图);
lty、lwd、col和pch分别指定线型、线宽、颜色和点的形状等。
# 创建一个矩阵
x <- matrix(c(1, 2, 3, 4, 5, 6), nrow = 3)# 使用 matplot() 绘制线图
matplot(x, type = "l", lwd = 2, col = c("red", "blue"), xlab = "X", ylab = "Y")
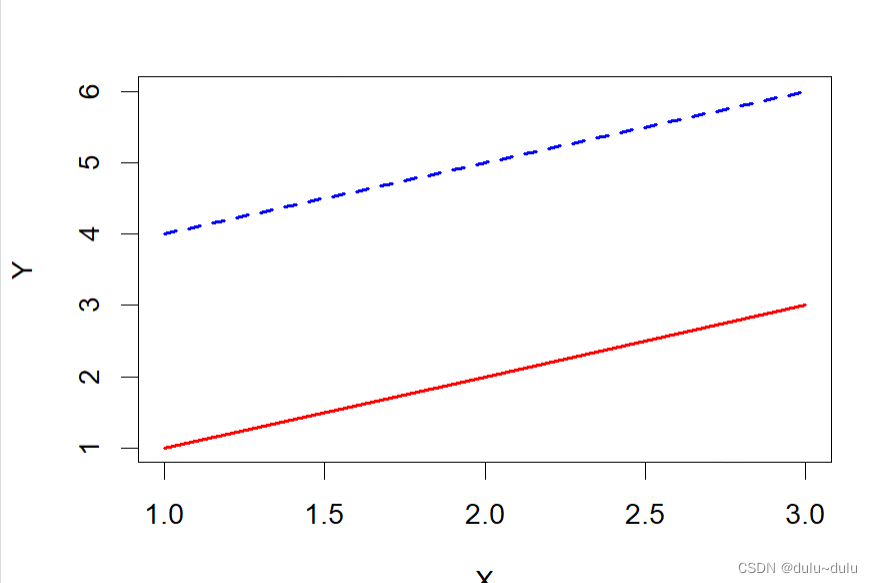
21.cor
cor(x, y = NULL, use = "everything", method = c("pearson", "kendall", "spearman"))
x和y是要计算相关系数的向量、矩阵或数据框;
use参数用于指定处理缺失值的方式,默认为"everything",表示包括所有的缺失值;method参数用于指定使用的相关系数类型,默认为"pearson",还可以是"kendall"(肯德尔相关系数)或"spearman"(斯皮尔曼相关系数)。
# 创建两个向量
x <- c(1, 2, 3, 4, 5)
y <- c(2, 4, 6, 8, 10)# 使用 cor() 计算两个向量的相关系数
correlation <- cor(x, y)
print(correlation)
[1] 1
向量
x和y是完全正相关的,相关系数为 1。
22.Contrast,row,col
#假设有一个包含销售数据的矩阵,其中行表示不同的产品,列表示不同的地区。
Contrast:对照矩阵:其每一行代表一种对照或比较,每一列表示一种变量或影响因素。对照矩阵描述了不同对照之间的差异
row:矩阵的行下标集:可以使用行下标集来选择该产品所在的行
col:求列下标集 :使用列下标集来选择这几个地区所在的列。
整理不易,若有遗漏或错误,请大佬们不吝赐教!!❤❤❤
相关文章:

R语言常用数组函数
目录 1.array 2.matrix 3.data.matrix 4.lower.tri 5.mat.or.vec 6.t:转置矩阵 7.cbind 8.rbind 9.diag 10.aperm:对数组进行轴置换(维度重排)操作 11.%*%:乘法操作要求矩阵 A 的列数等于矩阵 B 的行数 12.crossprod…...
前端开发之Element Plus的分页组件el-pagination显示英文转变为中文
前言 在使用element的时候分页提示语句是中文的到了element-plus中式英文的,本文讲解的就是怎样将英文转变为中文 效果图 解决方案 如果你的element-plus版本为2.2.29以下的 import { createApp } from vue import App from ./App.vue import ElementPlus from …...
基于Java+SpringBoot+Vue前后端分离社区医院管理系统设计和实现
博主介绍:✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专…...

浅谈单例模式在游戏开发中的应用
前言 如果在外部想在不同的时间结点、不同的位置访问某类中的成员且想要保持访问时,成员地址唯一。那么可以考虑将该类声明为静态类,但若是成员中包含公共的数据类型,此时便可以考虑将该类做成一个单例。 单例模式 由于类中的数据&#x…...

Stable Diffusion WebUI 整合包
现在网络上出现的各种整合包只是整合了运行 Stable Diffusion WebUI(以下简称为 SD-WebUI)必需的 Python 和 Git 环境,并且预置好模型,有些整合包还添加了一些常用的插件,其实际与手动进行本地部署并没有区别。 不过&a…...

什么是 RESTful API
什么是 RESTful API? RESTful API是一种设计哲学和架构风格,它基于 HTTP 协议和其状态管理原则,用于构建分布式系统。RESTful API 遵循以下设计原则: 资源层:API 应该代表一种资源,例如一个用户、一个订单…...

如何搭建关键字驱动自动化测试框架?
前言 那么这篇文章我们将了解关键字驱动测试又是如何驱动自动化测试完成整个测试过程的。关键字驱动框架是一种功能自动化测试框架,它也被称为表格驱动测试或者基于动作字的测试。关键字驱动的框架的基本工作是将测试用例分成四个不同的部分。首先是测试步骤&#x…...
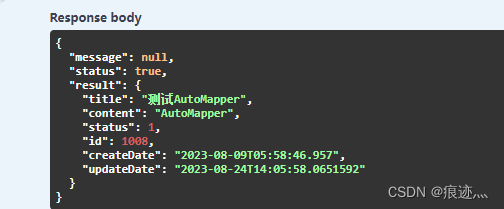
WPF实战项目十二(API篇):配置AutoMapper
1、新建类库WPFProjectShared,在类库下新建文件夹Dtos,新建BaseDto.cs,继承INotifyPropertyChanged,实现通知更新。 public class BaseDto : INotifyPropertyChanged{public int Id { get; set; }public event PropertyChangedEv…...

Linux 内核模块加载过程之重定位
文章目录 一、内核模块符号解析1.1 内核模块重定位函数调用1.1.1 struct load_info info1.1.2 copy_module_from_user 1.2 simplify_symbols1.2.1 simplify_symbols1.2.2 resolve_symbol_wait1.2.3 resolve_symbol1.2.4 find_symbol 二、 apply_relocations2.1 apply_relocatio…...
:PyFlink DataStream API之State)
Flink流批一体计算(19):PyFlink DataStream API之State
目录 keyed state Keyed DataStream 使用 Keyed State 实现了一个简单的计数窗口 状态有效期 (TTL) 过期数据的清理 全量快照时进行清理 增量数据清理 在 RocksDB 压缩时清理 Operator State算子状态 Broadcast State广播状态 keyed state Keyed DataStream 使用 k…...

adb shell获取安卓设备电量ROM内存帧率等信息
adb shell获取安卓设备电量ROM内存帧率等信息 adb shell指令获取Android设备的运行状态,如电池信息(包含电量百分比,电池状态,电池温度,电池电压,充放电电流),CPU占比,内…...
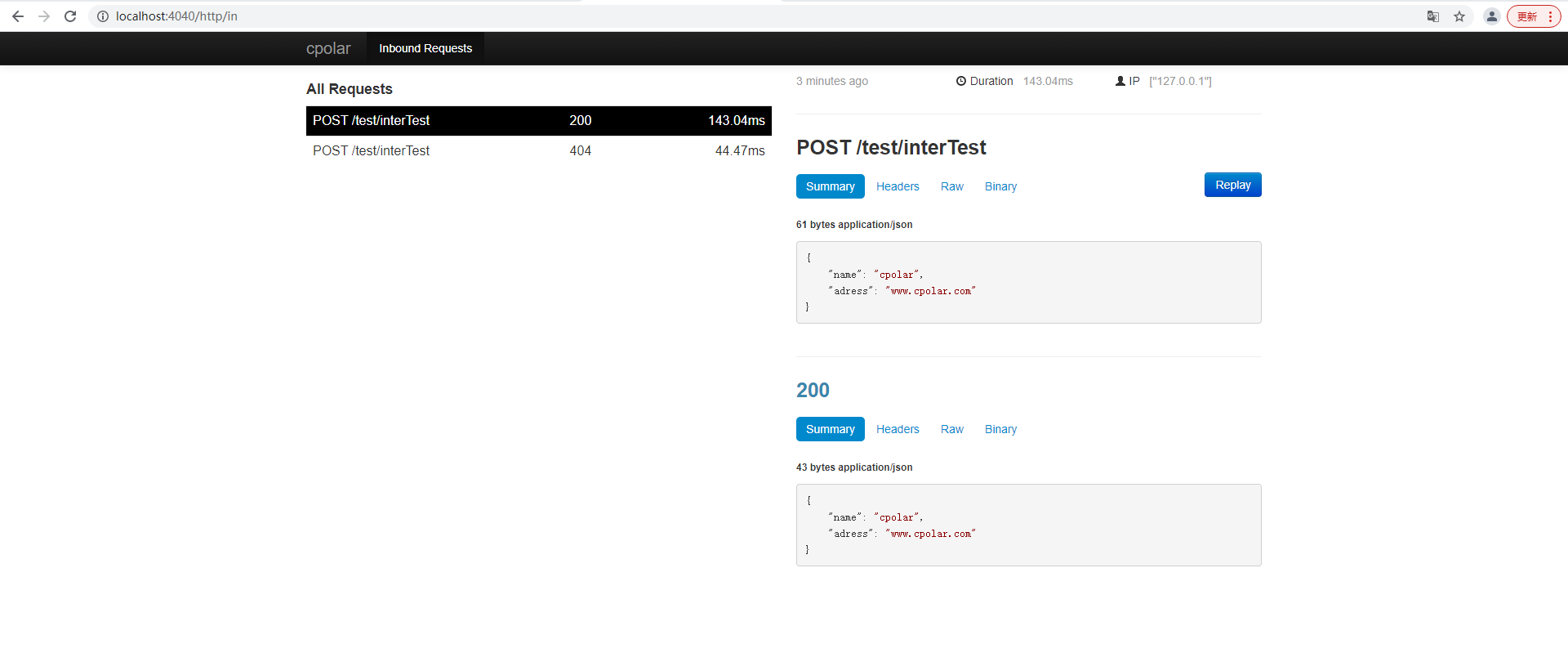
springboot服务端接口外网远程调试,并实现HTTP服务监听
文章目录 前言1. 本地环境搭建1.1 环境参数1.2 搭建springboot服务项目 2. 内网穿透2.1 安装配置cpolar内网穿透2.1.1 windows系统2.1.2 linux系统 2.2 创建隧道映射本地端口2.3 测试公网地址 3. 固定公网地址3.1 保留一个二级子域名3.2 配置二级子域名3.2 测试使用固定公网地址…...
代码随想录算法训练营之JAVA|第四十二天|70. 爬楼梯
今天是第 天刷leetcode,立个flag,打卡60天,如果做不到,完成一件评论区点赞最高的挑战。 算法挑战链接 70. 爬楼梯https://leetcode.cn/problems/climbing-stairs/ 第一想法 这是一个动态规划的入门题目,在看完完全背…...

【uniapp】 实现公共弹窗的封装以及调用
图例:红框区域为 “ 内容区域 ” 一、组件 <!-- 弹窗组件 --> <template> <view class"add_popup" v-if"person.isShowPopup"><view class"popup_cont" :style"{width:props.width&&props.width&…...

DevOps系列文章之 Python基础
列表 Python中的列表类似于C语言中的数组的概念,列表由内部的元素组成,元素可以是任何对象 Python中的列表是可变的 简单的理解就是:被初始化的列表,可以通过列表的API接口对列表的元素进行增删改查 1、定义列表 1.可以将列表当成…...

代码随想录第五十天
代码随想录第五十天 Leetcode 123. 买卖股票的最佳时机 IIILeetcode 188. 买卖股票的最佳时机 IV Leetcode 123. 买卖股票的最佳时机 III 题目链接: 买卖股票的最佳时机 III 自己的思路:想不到!!!!高维dp数组!&#x…...
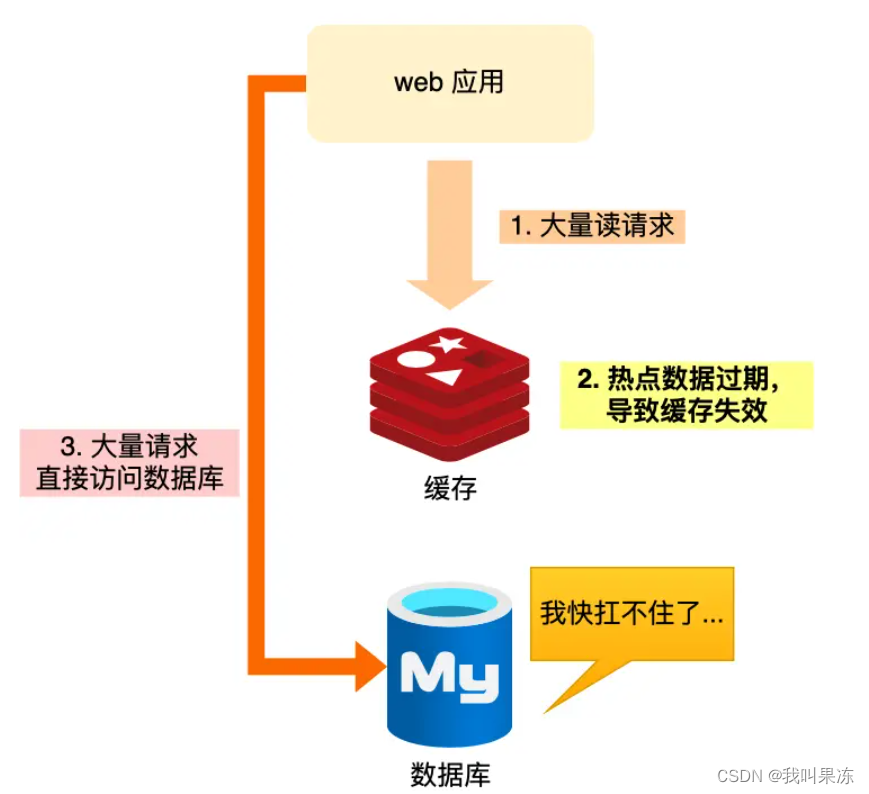
redis缓存雪崩、穿透、击穿解决方案
redis缓存雪崩、穿透、击穿解决方案 背景缓存雪崩缓存击穿缓存穿透总结背景 关于缓存异常,我们常见的有三个问题:缓存雪崩、缓存击穿、缓存穿透。这三个问题一旦发生,会导致大量请求直接落到数据库层面。如果请求的并发量很大,会影响数据库的运行,严重的会导致数据库宕机…...

基于HarmonyOS ArkUI实现七夕壁纸轮播
七夕情人节,为了Ta,你打算用什么方式表达爱?是包包、鲜花、美酒、巧克力,还是一封充满爱意的短信?作为程序员,以代码之名,表达爱。本节将演示如何在基于HarmonyOS ArkUI的SwiperController、Ima…...
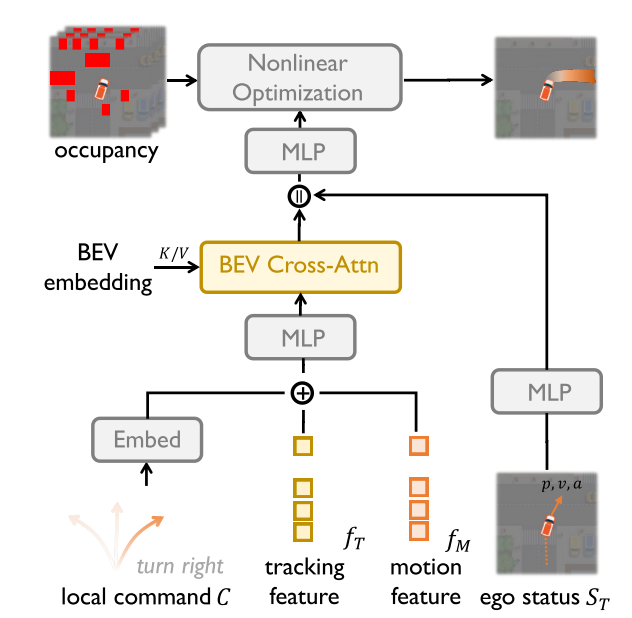
FusionAD:用于自动驾驶预测和规划任务的多模态融合
论文背景 自动驾驶(AD)任务通常分为感知、预测和规划。在传统范式中,AD中的每个学习模块分别使用自己的主干,独立地学习任务。 以前,基于端到端学习的方法通常基于透视视图相机和激光雷达信息直接输出控制命令或轨迹…...

C# 序列化json数据,datatabel转对象
datatabel直接转对象 转对象逻辑 1.将datatabel转为json格式 2.将json格式的内容转化为模型data_model的list对象 JsonConvert.DeserializeObject<List<data_model>>(JsonConvert.SerializeObject(dt))...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...