2022 ICPC 济南 E Identical Parity (扩欧)
2022 ICPC 济南 E. Identical Parity (扩欧)
Problem - E - Codeforces
大意:给出一个 n 和一个 k , 问是否能构造一个长 n 的排列使得所有长 k 的连续子序列和的奇偶性相同。
思路:通过分析可知 , 任两个间隔 k - 1 的元素奇偶性必然相同 , 这样的话 , 问题就转化成了
( n % k )个( ⌊ n k ⌋ + 1 )和( k − n % k )个( ⌊ n k ⌋ )是否能组成( ⌊ n 2 ⌋ )和( n − ⌊ n 2 ⌋ )的问题 (n ~\% ~k ~)个(\left \lfloor \frac{n}{k} \right \rfloor +1)和(k-n~\%~k)个(\left \lfloor \frac{n}{k} \right \rfloor)是否能组成(\left \lfloor \frac{n}{2} \right \rfloor)和(n - \left \lfloor \frac{n}{2} \right \rfloor)的问题 (n % k )个(⌊kn⌋+1)和(k−n % k)个(⌊kn⌋)是否能组成(⌊2n⌋)和(n−⌊2n⌋)的问题
很自然的就可以想到 01 背包去解决这个问题 , 但是显然 n 和 k 的范围太大了 , 无法使用 01 背包去解决这个问题。 于是转化问题 , 考虑现有范围的 x 和 y 是否能满足以下式子。
( ⌊ n k ⌋ + 1 ) ∗ x + ( ⌊ n k ⌋ ) ∗ y = ( ⌊ n 2 ⌋ ) (\left \lfloor \frac{n}{k} \right \rfloor +1)*x~+~(\left \lfloor \frac{n}{k} \right \rfloor)*y = (\left \lfloor \frac{n}{2} \right \rfloor) (⌊kn⌋+1)∗x + (⌊kn⌋)∗y=(⌊2n⌋)
带入扩欧得到通解:
x = x 0 ∗ c g c d ( a , b ) + k ∗ b g c d ( a , b ) x=x_0*{c\over gcd(a,b)}+{k*b\over gcd(a,b)} x=x0∗gcd(a,b)c+gcd(a,b)k∗b
y = y 0 ∗ c g c d ( a , b ) − k ∗ a g c d ( a , b ) y=y_0*{c\over gcd(a,b)}-{k*a\over gcd(a,b)} y=y0∗gcd(a,b)c−gcd(a,b)k∗a
根据已有的 x 的范围 和 y 的范围分别求出两个 k 的范围 , 判断这两个区间是否相交即可。
易错点:是否可以通过 x 的范围求出对应 k 的范围然后带入求 y 的范围 ?显然是可以的 , 但是这样求出的 y 的范围区间是不连续的 , 也就不能判交。
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int N = 2e6 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;int n , t , k;int exgcd(int a , int b , int &x , int &y){if(b == 0){ x = 1; y = 0; return a;}int g = exgcd(b , a % b , y , x);y -= a / b * x;return g;
}signed main(){IOScin >> t;while(t --){cin >> n >> k;if(n % k == 0){int num = n / k , od , ev;ev = n / 2;od = n - ev;if(ev % num == 0 && od % num == 0){cout << "Yes" << "\n";}else{cout << "No" << "\n";}}else{int a = n / k , b = n / k + 1 , c = n / 2;int cntb = n % k , cnta = k - n % k;int x , y , gcds;gcds = exgcd(a , b , x , y);a /= gcds;b /= gcds;c /= gcds;int k1_max = floor((double)(cnta - x * c) / (double) b);int k1_min = ceil((double)(0 - x * c) / (double) b);int k2_max = floor((double)(y * c) / (double) a);int k2_min = ceil((double)(y * c - cntb) / (double) a); if(k1_min > k1_max || k2_min > k2_max){cout << "No\n";}else{if(min(k2_max , k1_max) >= max(k1_min , k2_min)){cout << "Yes\n";}else{cout << "No\n";}}}}return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
相关文章:
)
2022 ICPC 济南 E Identical Parity (扩欧)
2022 ICPC 济南 E. Identical Parity (扩欧) Problem - E - Codeforces 大意:给出一个 n 和一个 k , 问是否能构造一个长 n 的排列使得所有长 k 的连续子序列和的奇偶性相同。 思路:通过分析可知 , 任两个间隔 k - 1 的元素奇偶…...

【BUG事务内消息发送】事务内消息发送,事务还未结束,消息发送已被消费,查无数据怎么解决?
问题描述 在一个事务内完成插入操作,通过MQ异步通知其他微服务进行事件处理。 由于是在事务内发送,其他服务消费消息,查询数据时还不存在如何解决呢? 解决方案 通过spring-tx包的TransactionSynchronizationManager事务管理器解…...
数据分析作业四-基于用户及物品数据进行内容推荐
## 导入支持库 import pandas as pd import matplotlib.pyplot as plt import sklearn.metrics as metrics import numpy as np from sklearn.neighbors import NearestNeighbors from scipy.spatial.distance import correlation from sklearn.metrics.pairwise import pairwi…...

在腾讯云服务器OpenCLoudOS系统中安装svn(有图详解)
1. 安装svn yum -y install subversion 安装成功: 2. 创建数据根目录及仓库 mkdir -p /usr/local/svn/svnrepository 创建test仓库: svnadmin create /usr/local/svn/test test仓库创建成功: 3. 修改配置test仓库 cd /usr/local/svn/te…...

C语言日常刷题5
文章目录 题目答案与解析1234567、 题目 1、以下叙述中正确的是( ) A: 只能在循环体内和switch语句体内使用break语句 B: 当break出现在循环体中的switch语句体内时,其作用是跳出该switch语句体,并中止循环体的执行 C: continue语…...
【LeetCode-中等题】73. 矩阵置零
题目 题解一:使用标记数组 public void setZeroes(int[][] matrix) {int m matrix.length;int n matrix[0].length;boolean[] row new boolean[m];boolean[] col new boolean[n];for(int i0; i< m;i){for(int j 0;j<n;j){if (matrix[i][j] 0) row[i]col…...

本地部署 FastGPT
本地部署 FastGPT 1. FastGPT 是什么2. 部署 FastGPT 1. FastGPT 是什么 FastGPT 是一个基于 LLM 大语言模型的知识库问答系统,提供开箱即用的数据处理、模型调用等能力。同时可以通过 Flow 可视化进行工作流编排,从而实现复杂的问答场景! …...

软件工程(十八) 行为型设计模式(四)
1、状态模式 简要说明 允许一个对象在其内部改变时改变它的行为 速记关键字 状态变成类 类图如下 状态模式主要用来解决对象在多种状态转换时,需要对外输出不同的行为的问题。比如订单从待付款到待收货的咋黄台发生变化,执行的逻辑是不一样的。 所以我们将状态抽象为一…...
Socket通信与WebSocket协议
文章目录 目录 文章目录 前言 一、Socket通信 1.1 BIO 1.2 NIO 1.3 AIO 二、WebSocket协议 总结 前言 一、Socket通信 Socket是一种用于网络通信的编程接口(API),它提供了一种机制,使不同主机之间可以通过网络进行数据传输和通信…...

新KG视点 | Jeff Pan、陈矫彦等——大语言模型与知识图谱的机遇与挑战
OpenKG 大模型专辑 导读 知识图谱和大型语言模型都是用来表示和处理知识的手段。大模型补足了理解语言的能力,知识图谱则丰富了表示知识的方式,两者的深度结合必将为人工智能提供更为全面、可靠、可控的知识处理方法。在这一背景下,OpenKG组织…...

详解过滤器Filter和拦截器Interceptor的区别和联系
目录 前言 区别 联系 前言 过滤器(Filter)和拦截器(Interceptor)都是用于在Web应用程序中处理请求和响应的组件,但它们在实现方式和功能上有一些区别。 区别 1. 实现方式: - 过滤器是基于Servlet规范的组件,通过实现javax.servlet.Filt…...

List常用的操作
1、看List里是否存在某个元素 contains //省略建立listboolean contains stringList.contains("上海");System.out.println(contains); 如果存在是true,不存在是false 2、看某个元素在List中的索引号 .indexOf List<String>stringList new Ar…...

Android studio APK切换多个摄像头(Camera2)
1.先设置camera的权限 <uses-permission android:name"android.permission.CAMERA" /> 2.布局 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas.android.com/apk/res/android"and…...

ChatGPT 对教育的影响,AI 如何颠覆传统教育
胜量老师 来源:BV1Nv4y1H7kC 由Chat GPT引发的对教育的思考,人类文明发展至今一直靠教育完成文明的传承,一个年轻人要经历若干年的学习,才能进入社会投入对文明的建设,而学习中有大量内容是需要记忆和反复训练的。 无…...
Spring(九)声明式事务
Spring整合Junit4和JdbcTemplater如下所示: 我们所使用的junit的jar包不同,可以整合不同版本的junit。 我们导入的依赖如下所示: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.a…...
)
java中用HSSFWorkbook生成xls格式的excel(亲测)
SXSSFWorkbook类是用于生成XLSX格式的Excel文件(基于XML格式),而不是XLS格式的Excel文件(基于二进制格式)。 如果你需要生成XLS格式的Excel文件,可以使用HSSFWorkbook类。以下是一个简单的示例:…...

做平面设计一般电脑可以吗 优漫动游
平面设计常用的软件如下:Photoshop、AutoCAD、AI等。其中对电脑配置要求高的是AutoCAD,可运行AutoCAD的软件均可运行如上软件。 做平面设计一般电脑可以吗 AutoCAD64位版配置要求:AMDAthlon64位处理器、支持SSE2技术的AMDOpteron处理器、…...
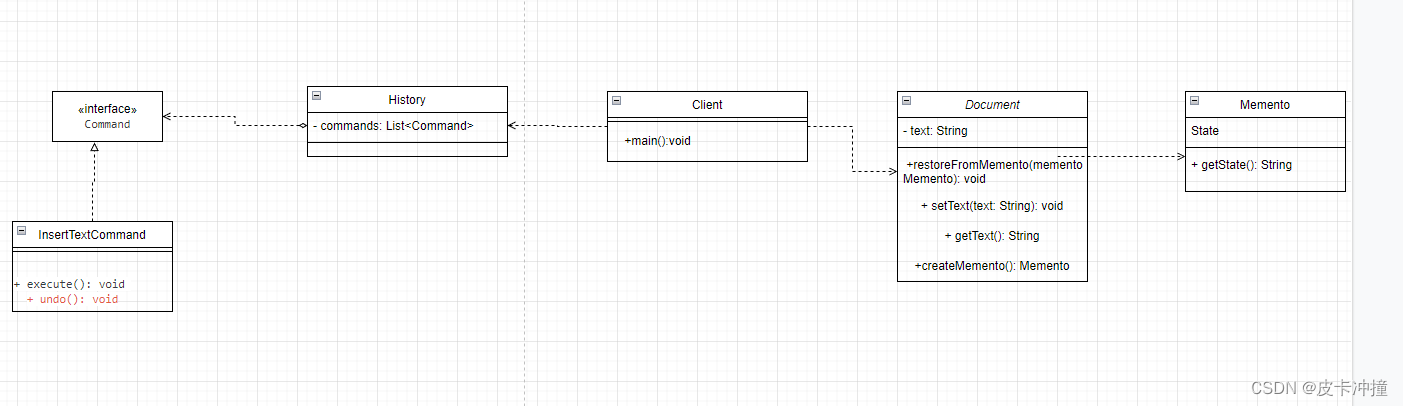
设计模式备忘录+命令模式实现Word撤销恢复操作
文章目录 前言思路代码实现uml类图总结 前言 最近学习设计模式行为型的模式,学到了备忘录模式提到这个模式可以记录一个对象的状态属性值,用于下次复用,于是便想到了我们在Windows系统上使用的撤销操作,于是便想着使用这个模式进…...

Linux centos7 bash编程小训练
训练要求: 求比一个数小的最大回文数 知识点: 一个数字正读反读都一样,我们称为回文数,如5、11、55、121、222等。 我们训练用bash编写一个小程序,由我们标准输入一个整数,计算机将显示出一个比这个数小…...

创作2周年纪念日-特别篇
创作2周年纪念日-特别篇 1. 与CSDN的机缘2. 收获3. 憧憬 1. 与CSDN的机缘 很荣幸,在大学时候,能够接触到CSDN这样一个平台,当时对嵌入式开发、编程、计算机视觉等内容比较感兴趣。后面一个很偶然的联培实习机会,让我接触到了Pych…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

鸿蒙HarmonyOS 5军旗小游戏实现指南
1. 项目概述 本军旗小游戏基于鸿蒙HarmonyOS 5开发,采用DevEco Studio实现,包含完整的游戏逻辑和UI界面。 2. 项目结构 /src/main/java/com/example/militarychess/├── MainAbilitySlice.java // 主界面├── GameView.java // 游戏核…...
