随机化快速排序(Java 实例代码)
随机化快速排序
一、概念及其介绍
快速排序由 C. A. R. Hoare 在 1960 年提出。
随机化快速排序基本思想:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
二、适用说明
快速排序是一种比较快速的排序算法,它的平均运行时间是 O(nlogn),之所以特别快是由于非常精练和高度优化的内部循环,最坏的情形性能为 O(n^2)。像归并一样,快速排序也是一种分治的递归算法。从空间性能上看,快速排序只需要一个元素的辅助空间,但快速排序需要一个栈空间来实现递归,空间复杂度也为O(logn)。
三、过程图示
在一个数组中选择一个基点,比如第一个位置的 4,然后把4挪到正确位置,使得之前的子数组中数据小于 4,之后的子数组中数据大于 4,然后逐渐递归下去完成整个排序。
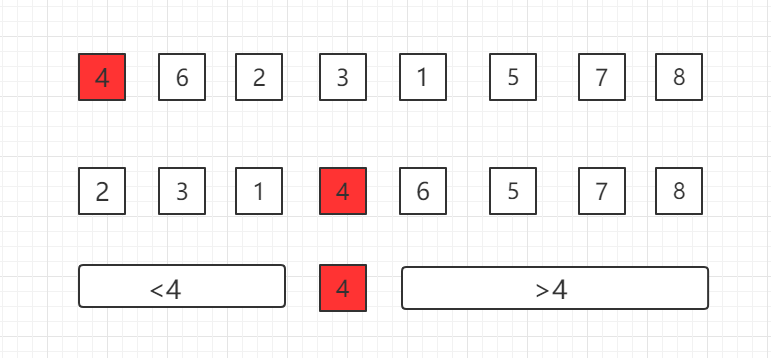
如何和把选定的基点数据挪到正确位置上,这是快速排序的核心,我们称为 Partition。
过程如下所示,其中 i 为当前遍历比较的元素位置:
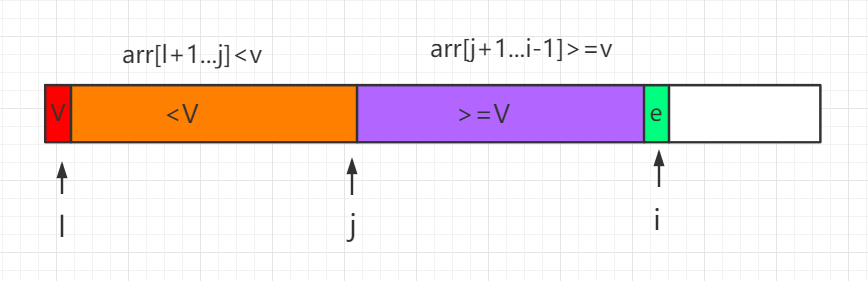
这个 partition 过程用代码表示为:
实例
...
private static int partition(Comparable[] arr, int l, int r){
Comparable v = arr[l];
int j = l;
for( int i = l + 1 ; i <= r ; i ++ )
if( arr[i].compareTo(v) < 0 ){
j ++;
//数组元素位置交换
swap(arr, j, i);
}
swap(arr, l, j);
return j;
}
...
如果是对近乎有序的数组进行快速排序,每次 partition 分区后子数组大小极不平衡,容易退化成 O(n^2) 的时间复杂度算法。我们需要对上述代码进行优化,随机选择一个基点做为比较,称为随机化快速排序算法。只需要在上述代码前加上下面一行,随机选择数组中一数据和基点数据进行交换。
swap( arr, l , (int)(Math.random()*(r-l+1))+l );
四、Java 实例代码
源码包下载:Download![]() https://www.runoob.com/wp-content/uploads/2020/09/runoob-algorithm-random-quick-sort.zip
https://www.runoob.com/wp-content/uploads/2020/09/runoob-algorithm-random-quick-sort.zip
QuickSort.java 文件代码:
package runoob;
/**
* 随机化快速排序
*/
public class QuickSort {
// 对arr[l...r]部分进行partition操作
// 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
private static int partition(Comparable[] arr, int l, int r){
// 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
swap( arr, l , (int)(Math.random()*(r-l+1))+l );
Comparable v = arr[l];
// arr[l+1...j] < v ; arr[j+1...i) > v
int j = l;
for( int i = l + 1 ; i <= r ; i ++ )
if( arr[i].compareTo(v) < 0 ){
j ++;
swap(arr, j, i);
}
swap(arr, l, j);
return j;
}
// 递归使用快速排序,对arr[l...r]的范围进行排序
private static void sort(Comparable[] arr, int l, int r){
if (l >= r) {
return;
}
int p = partition(arr, l, r);
sort(arr, l, p-1 );
sort(arr, p+1, r);
}
public static void sort(Comparable[] arr){
int n = arr.length;
sort(arr, 0, n-1);
}
private static void swap(Object[] arr, int i, int j) {
Object t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
// 测试 QuickSort
public static void main(String[] args) {
// Quick Sort也是一个O(nlogn)复杂度的算法
// 可以在1秒之内轻松处理100万数量级的数据
int N = 1000000;
Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 100000);
sort(arr);
SortTestHelper.printArray(arr);
}
}
相关文章:
随机化快速排序(Java 实例代码)
随机化快速排序 一、概念及其介绍 快速排序由 C. A. R. Hoare 在 1960 年提出。 随机化快速排序基本思想:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数…...
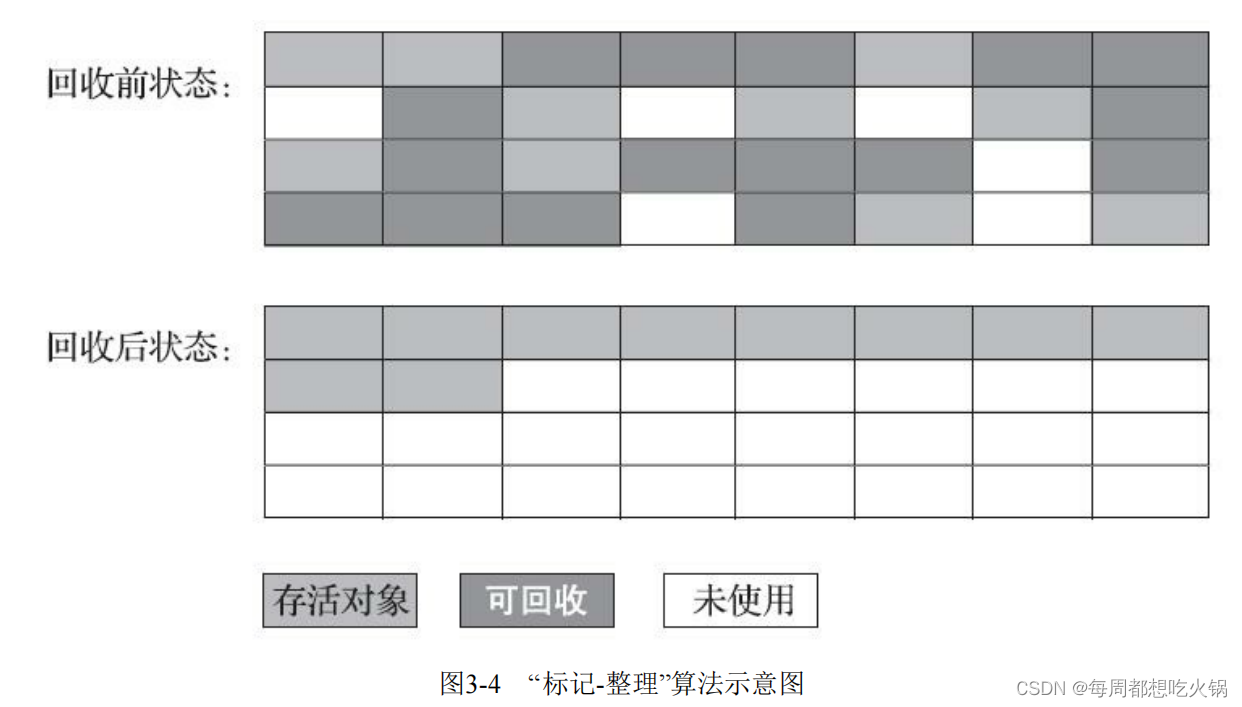
JVM 垃圾收集
垃圾收集 分代理论Java 堆的内存分区不同分代收集垃圾收集算法 分代理论 弱分代假说:绝大多数对象都是朝生夕灭,即绝大多数对象都是用完很快需要销毁的。强分代假说:熬过多次垃圾收集过程的对象就越难以消亡,即如果对象经过多次垃…...
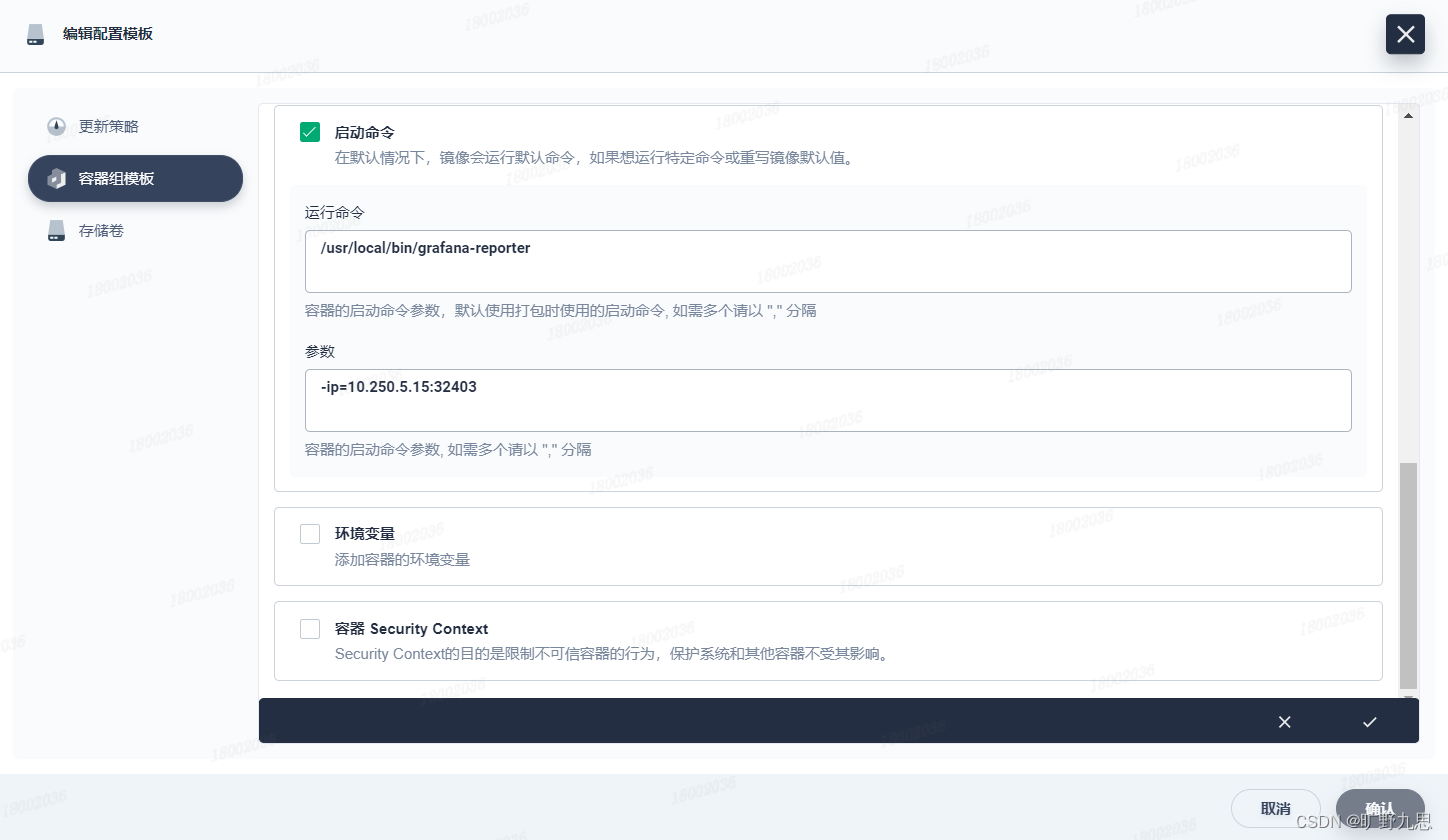
kubesphere中部署grafana实现dashboard以PDF方式导出
1,部署grafana-image-renderer 2,部署grafana GF_RENDERING_SERVER_URL http://ip:30323/render #grafana-image-renderer地址 GF_RENDERING_CALLBACK_URL http://ip:32403/ #grafana地址 GF_LOG_FILTERS rend…...
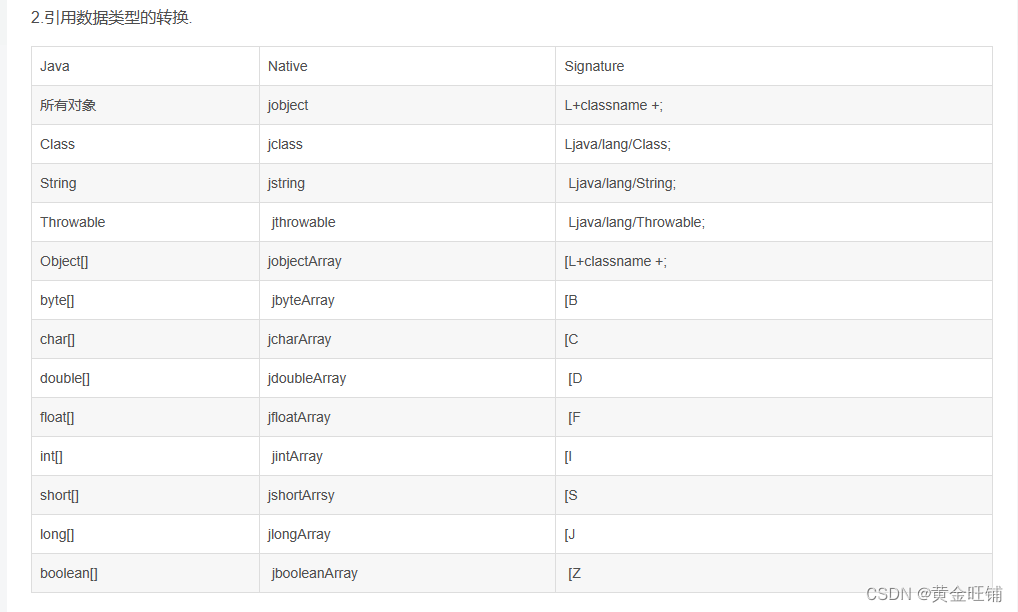
【环境配置】Android-Studio-OpenCV-JNI以及常见错误 ( 持续更新 )
最近一个项目要编译深度学习的库,需要用到 opencv 和 JNI,本文档用于记录环境配置中遇到的常见错误以及解决方案 Invalid Gradle JDK configuration found failed Invalid Gradle JDK configuration foundInvalid Gradle JDK configuration found. Open…...
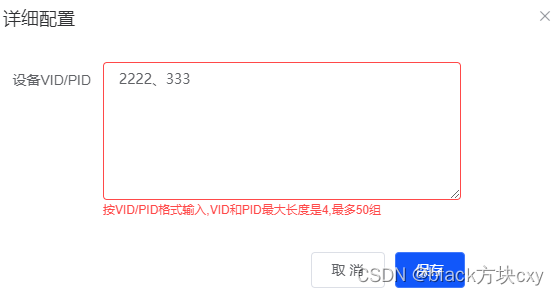
js 正则表达式 验证 :页面中一个输入框,可输入1个或多个vid/pid,使用英文逗号隔开...
就是意思一个输入框里面,按VID/PID格式输入,VID和PID最大长度是4,最多50组 1、页面代码 <el-form ref"ruleForm" :model"tempSet" :rules"rules" label-position"right"> <!-- 最多 50组,每组9个字符…...
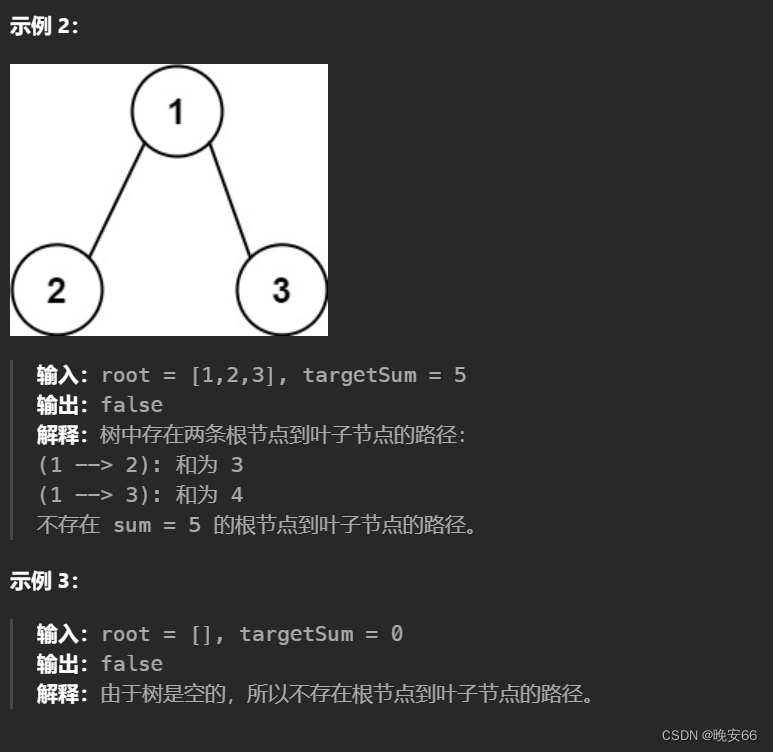
【算法与数据结构】112、LeetCode路径总和
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:本题通过计算根节点到叶子节点路径上节点的值之和,然后再对比目标值。利用文章【算法和数据…...
②matlab桌面和编辑器
目录 matlab编辑器练习 运行脚本 matlab编辑器练习 您可以通过点击灰色代码框在脚本中输入命令。 准备就绪后,您可以通过点击蓝色的提交按钮提交代码。 任务 在脚本中输入命令 r 3。 2.任务 在脚本中添加命令 x pi*r^2。 附加练习 当您在实时编辑器中完成…...

高亮img、pdf重点部分(html2canvas、pdfjs-dist、react-pdf)
可用业务场景 报销单据审批中,高亮发票部分 需求 后台返回一张图片或者pdf、返回一组坐标,坐标类型[number,number,number,number],分别代表了x、y、width、height。需要根据坐标在图片上高亮出来坐标位置。如下图 高亮的坐标是࿱…...

18.神奇导航菜单指示器
效果 源码 <!DOCTYPE html> <html> <head> <title>Magic Menu Indicator | 03</title> <link rel="stylesheet" type="text/css" href="style.css"> </head> <body><div class="navig…...
WPF+Prism+WebApi 学习总结
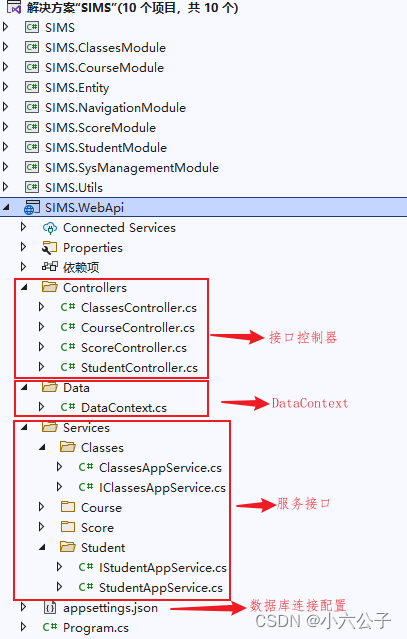
一、基本概念 WPF:WPF(Windows Presentation Foundation)是(微软推出的)基于Windows的用户界面框架,提供了统一的编程模型,语言和框架,做到了分离界面设计人员与开发人员的工作;WPF…...
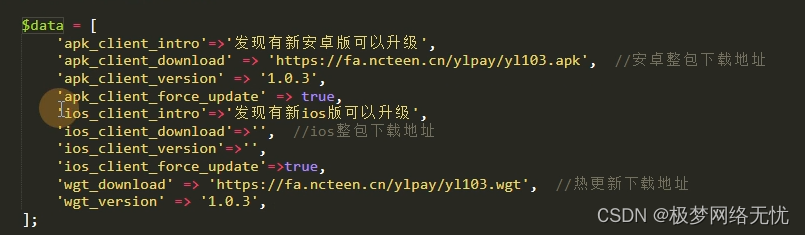
uniapp热更新
首先热更新需要wgt包; 其次先了解这两个组件 下载的方法 安装的组件 场景: 当你项目的js文件或者页面文件或者静态图片文件css文件更新的时候可以走热更新; 而当你安装新的组件插件或者开启新的权限等功能的时候就无法通过热更新进行更新了…...
)
AUTOSAR从入门到精通-【应用篇】基于CAN协议的汽车尾气后处理诊断系统的软件开发(续)
目录 尾气后处理诊断程序的开发 5.1 数据库的解析 5.1.1 寻找XML文件 5.1.2 读取XML文件...
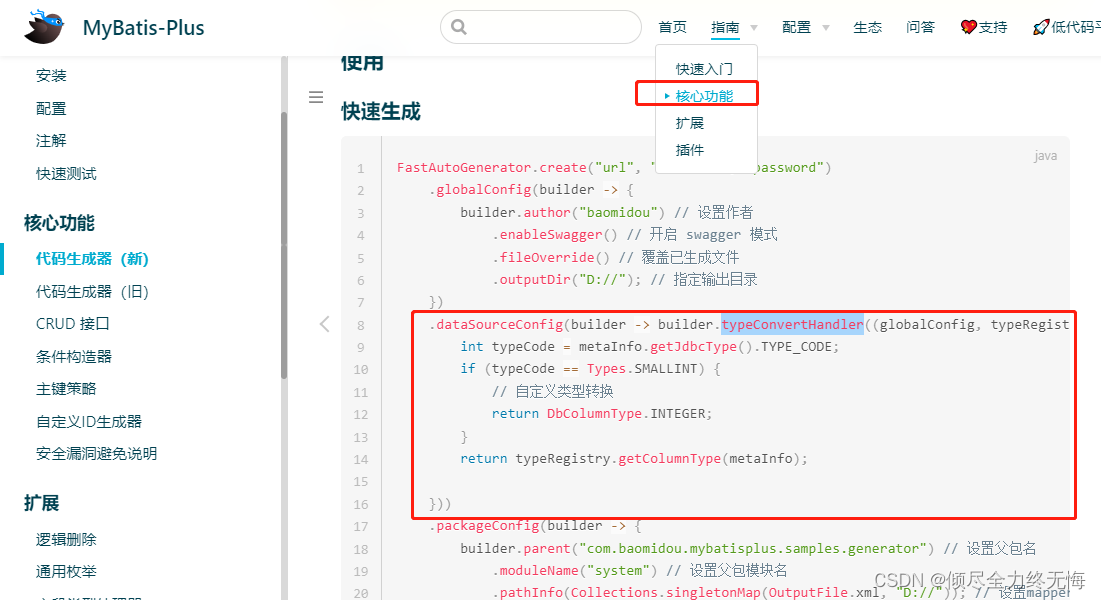
mybatis plus新版代码生成器,类型转换处理器ITypeConvertHandler使用
目录 引言关键代码源码分析记录一坑类型转换的第二种方式完整源码地址 引言 当默认生成的数据类型不满足时,就需要自定义指定要生成的类型 关键代码 FastAutoGenerator.create(url, username, password).dataSourceConfig(builder -> {builder.typeConvertHandl…...
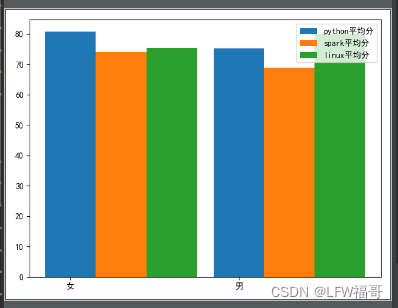
python中的matplotlib画直方图(数据分析与可视化)
python中的matplotlib画直方图(数据分析与可视化) import numpy as np import pandas as pd import matplotlib.pyplot as pltpd.set_option("max_columns",None) plt.rcParams[font.sans-serif][SimHei] plt.rcParams[axes.unicode_minus]Fa…...

【详解】文本检测OCR模型的评价指标
关于文本检测OCR模型的评价指标 前言:网上关于评价标准乱七八糟的,有关于单词的,有关于段落的,似乎没见过谁解释一下常见论文中常用的评价指标具体是怎么计算的,比如DBNet,比如RCNN,这似乎好像…...
)
Python遥感图像处理应用篇038 GDAL 遥感图像特征提取(统计特征图)
1.图像统计特征 遥感图像的统计特征是对图像中像素值的统计分布进行定量化描述的过程。这些统计特征可以提供关于图像内容和特性的有用信息。下面是一些常用的遥感图像统计特征描述方法: 平均值(Mean):计算图像中所有像素值的平均值,可以反映整个图像的亮度水平。 方差(…...

全局ID生成方式
全局ID生成方式 目录 1. 全局唯一id介绍 1.1 特点 2. 常见的全局唯一id生成策略 2.1 利用数据库自增字段生成id2.2 UUID2.3 Redis生成id2.4 zookeeper生成ID2.5 Twitter的snowflake算法 3. 面试题目:实现一个全局的ID生成器,注意线程安全 3.1 单例模式…...
c++之指针
总结性质 我们如何在一个函数中获取数组的长度: 我们都知道,在main函数中我们获得数组的长度只需要使用sizeof(a)/sizeof(a【0】)即可获得,但当我们把一个数组传入到方法时,c默认把…...
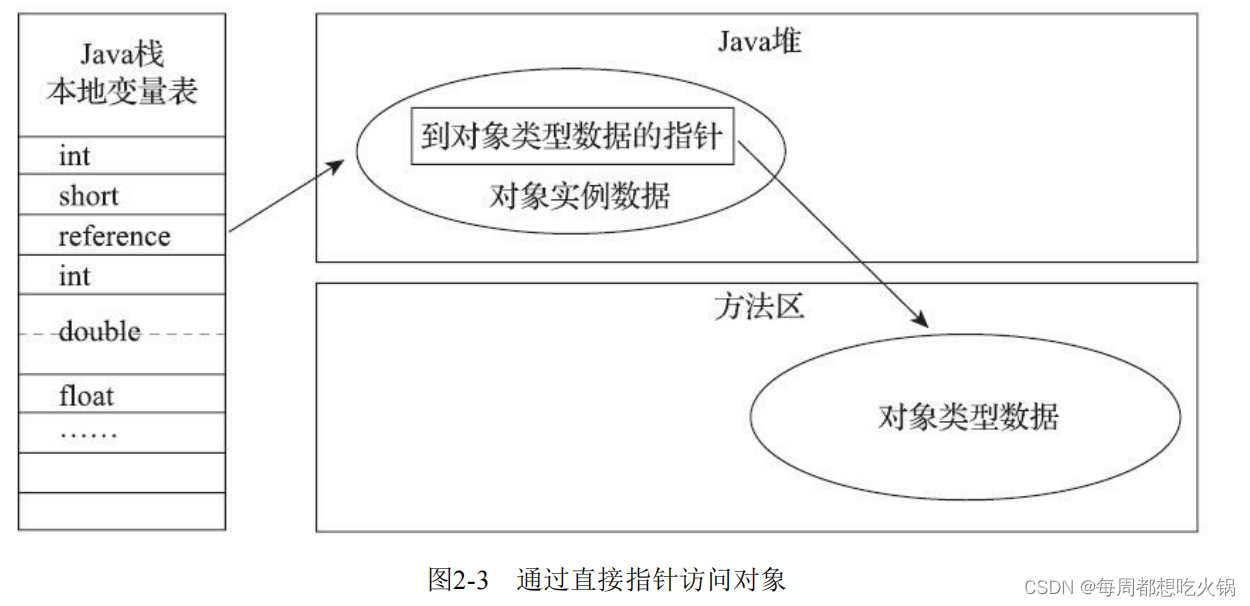
JVM 访问对象的两种方式
Java 程序会通过栈上的 reference 数据来操作堆上的具体对象。由于 reference 类型在《Java 虚拟机规范》里面只规定了它是一个指向对象的引用,并没有定义这个引用应该通过什么方式去定位、访问到堆中对象的具体位置,所以对象访问方式也是由虚拟机实现而…...

yo!这里是Linux基础开发工具介绍
目录 前言 基础开发工具 yum vim 1.基本介绍 2.基本操作 3.正常模式常用命令 4.底行模式常用命令 gcc/g gdb 1.基本介绍 2.常用操作 make/Makefile 1.背景 2.介绍 3.使用 git 1.介绍 2.操作 进度条程序简单实现 后记 前言 在学完初步的基础指令及权限控…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...

LangChain【6】之输出解析器:结构化LLM响应的关键工具
文章目录 一 LangChain输出解析器概述1.1 什么是输出解析器?1.2 主要功能与工作原理1.3 常用解析器类型 二 主要输出解析器类型2.1 Pydantic/Json输出解析器2.2 结构化输出解析器2.3 列表解析器2.4 日期解析器2.5 Json输出解析器2.6 xml输出解析器 三 高级使用技巧3…...
