A - 最短路径
给出一张包含 n 个节点、 m 条边的无向图,请你求出图上两点 s,t 间的最短路径长度。
(请大家自行处理重边和自环)
Input
第一行两个数 n,m ,分别表示节点数和边数,以空格隔开,其中1≤n≤500,1≤m≤50000 ;
之后 m 行,每行 3 个数 u,v,w[i] ,表示点 u 和 v 间有一条权值为 w[i] 的边,
其中1≤u,v≤n ,1≤w[i]≤500000 ;最后一行,两个数 s,t 表示选择的两个点,以空格隔开。
Output
输出一个数,表示 s,t 间最短路径的长度。
Data Description
对于 27% 的数 n≤10 , m≤50 ;
对于 70% 的数据, n≤100 ,m≤5000 ;
对于 100% 的数据,n≤500 ,m≤50000 ,1≤w[i]≤500000 ;
Sample 1
| Inputcopy | Outputcopy |
|---|---|
4 3 1 2 6 1 3 4 2 4 2 3 4 | 12 |
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 510;
const int INF = 0x3f3f3f3f;
int a[N][N];int n, m;void floyd()
{for (int k = 1; k <= n; k++)for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++)a[i][j] = min(a[i][j], a[i][k] + a[k][j]);
}int main()
{memset(a, INF, sizeof a);cin >> n >> m;for (int i = 1; i <= m; i++){int num1, num2, num3;cin >> num1 >> num2 >> num3;a[num1][num2] = a[num2][num1] = min(a[num1][num2],num3);}floyd();for(int i=1;i<=n;i++) a[i][i] = 0;int num3, num4;cin >> num3 >> num4;cout << a[num3][num4] << endl;
}
相关文章:

A - 最短路径
给出一张包含 n 个节点、 m 条边的无向图,请你求出图上两点 s,t 间的最短路径长度。 (请大家自行处理重边和自环) Input 第一行两个数 n,m ,分别表示节点数和边数,以空格隔开,其中1≤n≤500,1≤m≤50000 ; 之后 m 行…...
自然语言处理(三):基于跳元模型的word2vec实现
跳元模型 回顾一下第一节讲过的跳元模型 跳元模型(Skip-gram Model)是一种用于学习词向量的模型,属于Word2Vec算法中的一种。它的目标是通过给定一个中心词语来预测其周围的上下文词语。 这节我们以跳元模型为例,讲解word2vec的…...

1.1 数据库系统简介
思维导图: 1.1.数据库系统简介 前言: 数据库系统是一个软件系统,用于管理和操作数据库。它提供了一个组织良好、高效并能够方便存取的数据存储机制,并且能够支持各种数据操作、事务管理、并发控制和恢复功能。以下是数据库系统的…...

WebGL 绘制圆点
前言 这篇文章不说WebGL相关概念了,初学者先到网上看看WebGL相关概念。这里着重写一下在vue3前端框架下,如何通过webGL绘制圆点。 着色器代码(画点) 画点相关的着色器代码有顶点着色器和片元着色器,代码如下: 顶点着色器&…...

迅为RK3588开发板Android12 设置系统默认不锁屏
修改 frameworks/base/packages/SettingsProvider/res/values/defaults.xml 文件,修改为如下 所示: - <bool name"def_lockscreen_disabled">false</bool> <bool name"def_lockscreen_disabled">true</bool&…...

香港服务器速度快的原因
1. 传统域名解析过程 了解CDN系统先从域名解析说起。通常,我们在浏览器中输入域名,敲回车后,进入网站进行信息的获取。您分析过输入域名后浏览是如何请求到服务器上的信息,您了解域名解析的过程么? 1.1. 主机解析域…...

过滤器,监听器与拦截器的区别
过滤器,监听器与拦截器的区别 过滤器和监听器不是Spring MVC中的组件,而是Servlet的组件,由Servlet容器来管理。拦截器是Spring MVC中的组件,由Spring容器来管理 Servlet过滤器与Spring MVC 拦截器在Web应用中所处的层次如…...

clickhouse ssb-dbgen数据构造 及 clickhouse-benchmark简单压测
一、 测试数据构造 1. 数据样例 官方文档有给出一批数据样例。优点是比较真实,缺点是太大了,动辄上百G不适合简单小测试 Anonymized Yandex.Metrica DatasetStar Schema BenchmarkWikiStatTerabyte of Click Logs from CriteoAMPLab Big Data Benchma…...
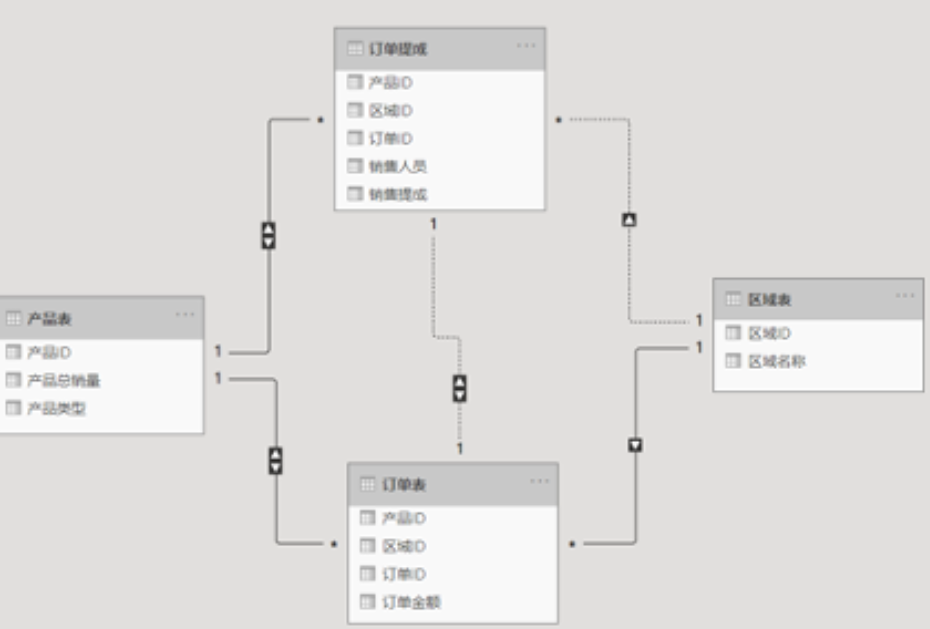
【数据分析】统计量
1. 均值、众数描述数据的集中趋势度量,四分位差、极差描述数据的离散程度。 2. 标准差、四分位差、异众比率度量离散程度,协方差是度量相关性。 期望值分别为E[X]与E[Y]的两个实随机变量X与Y之间的协方差Cov(X,Y)定义为: 从直观上来看&…...

【通用消息通知服务】0x4 - 目前进展 阶段复盘
【通用消息通知服务】0x4 - 阶段复盘 达成 基本的API已经写完✍️了(消息查看发送, 模板crud,终端crud,发送渠道crud,计划crud,计划执行查看)拆分server, executor, planner三个入口, 方便针对性水平扩展整体架构初步形成,通过队列实现了事件驱动模型和消息订阅发…...
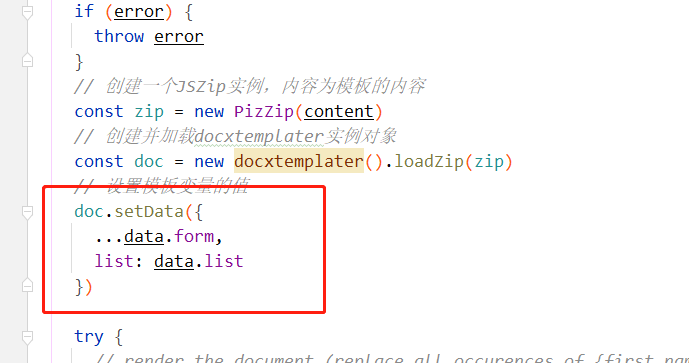
vue若依导出word文件,简单的实现
首先前端导包,注意exportDocx的导包位置要修改成你自己的 import {exportDocx} from /utils/docUtil/docutil.js; import {addDays} from date-fns; import {listGongyi} from "/api/system/detail";然后新建一个测试按钮 <el-col :span"1.5"><…...
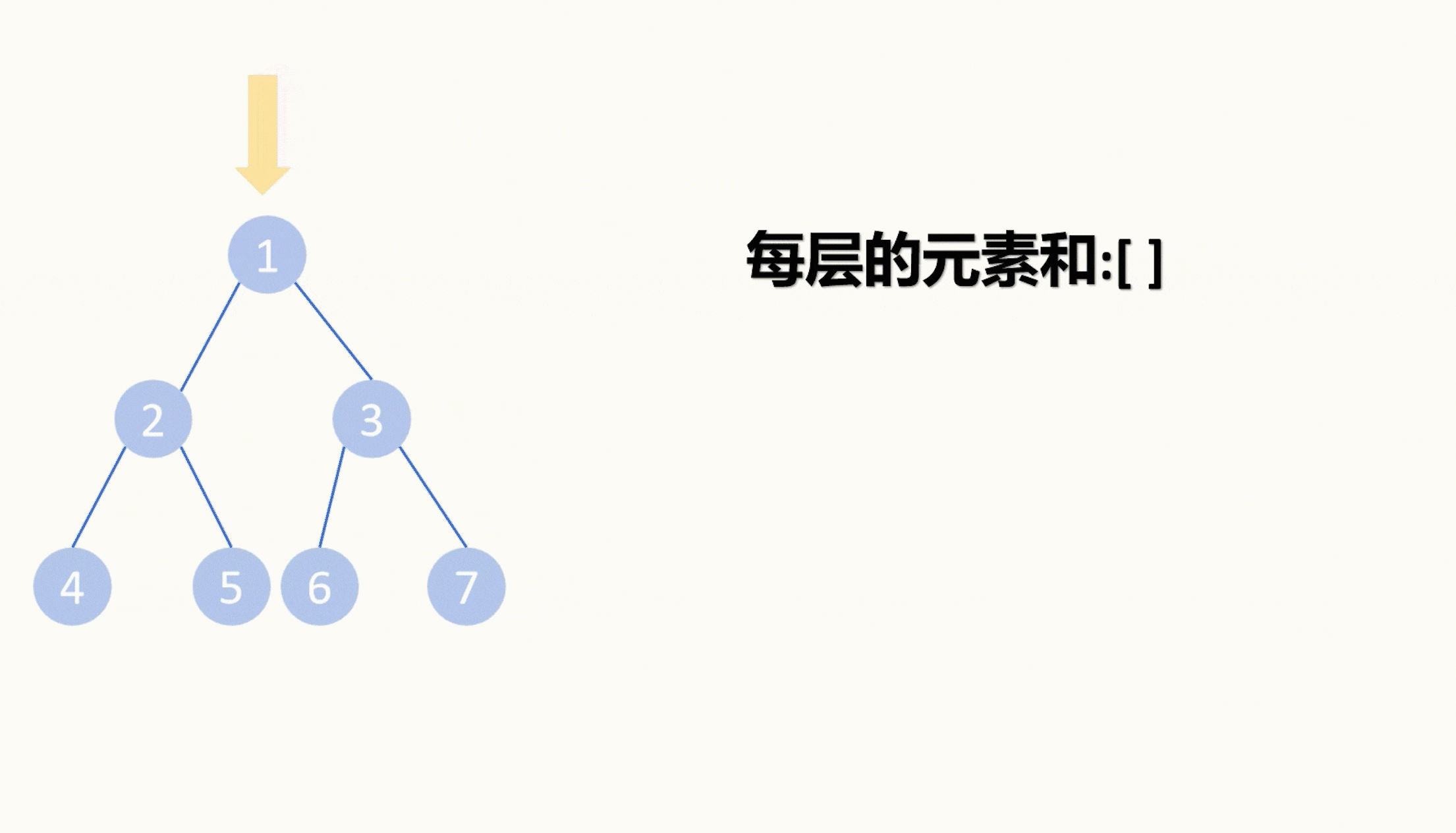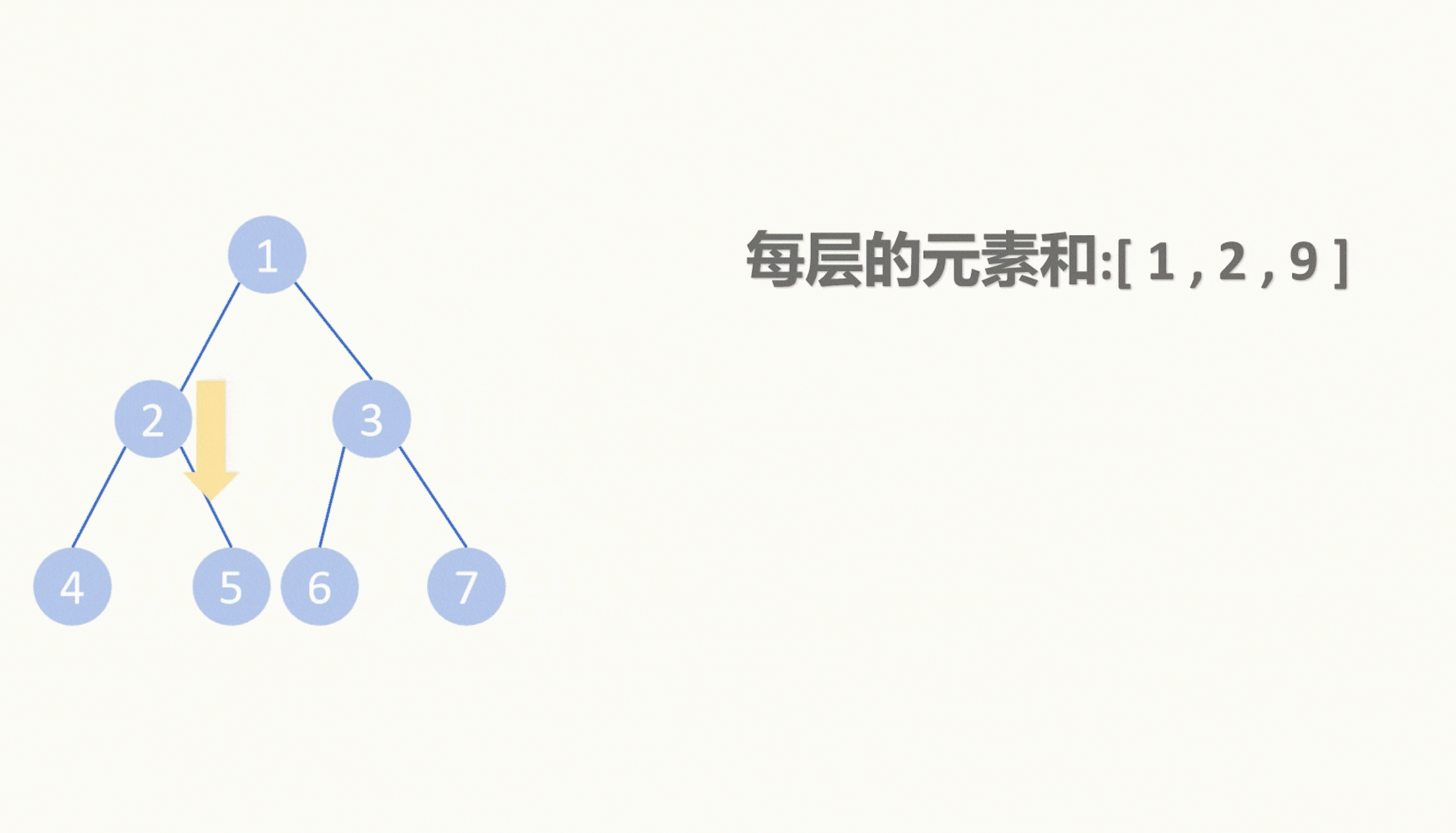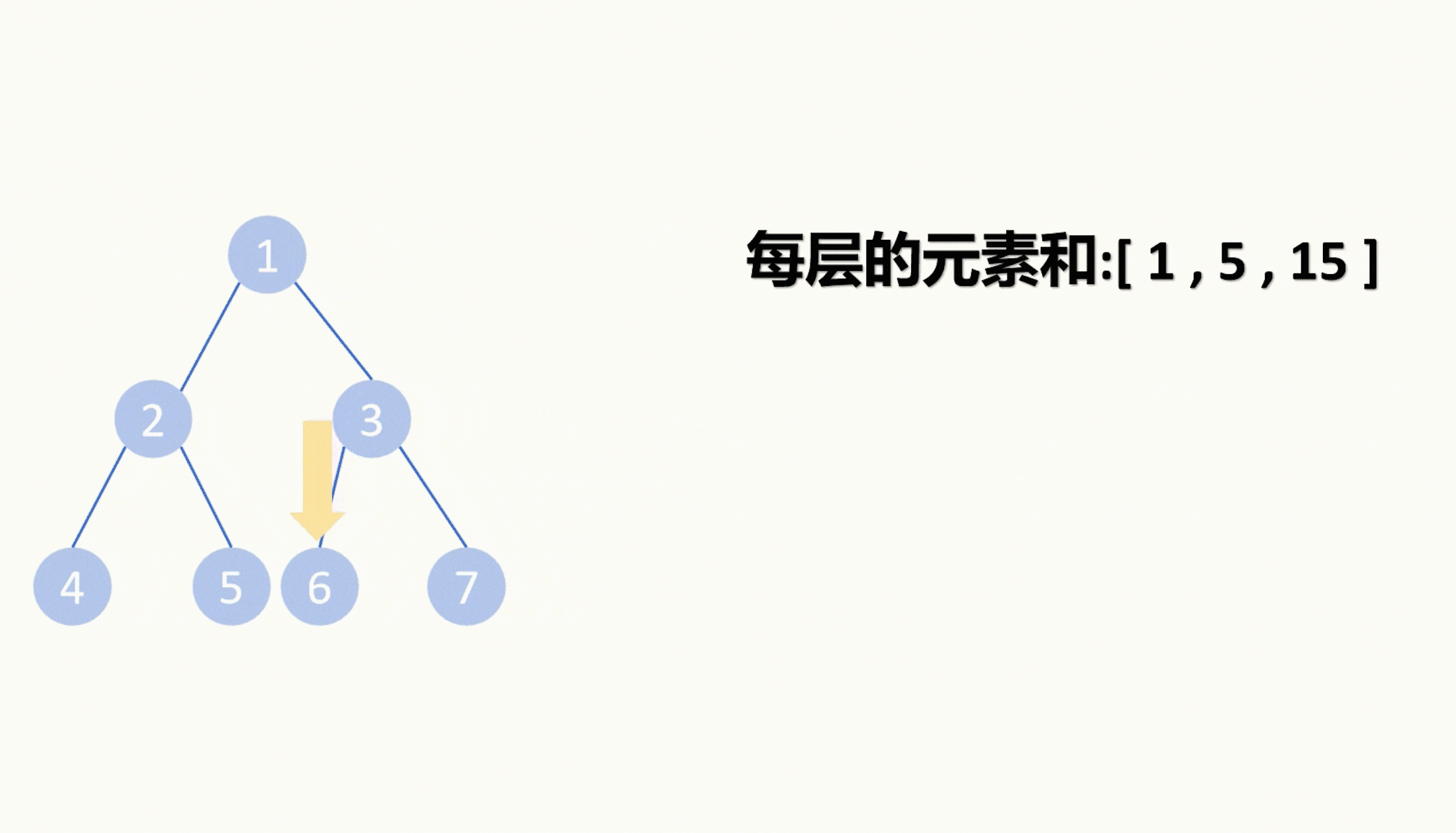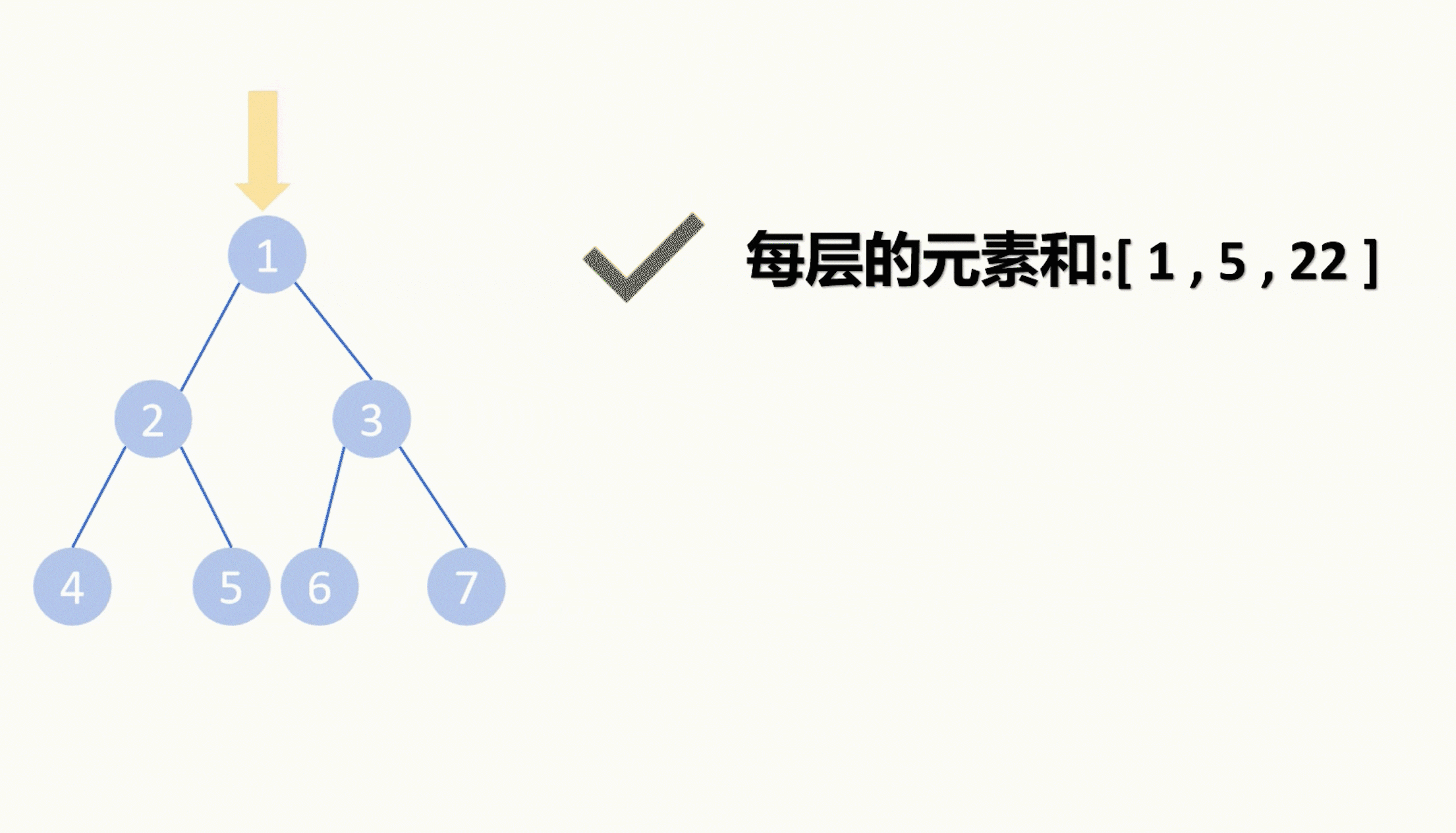
【LeetCode75】第四十题 最大层内元素和
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 这道题和LeetCode75的上一题大同小异,都是要我们对二叉树进行层序遍历。 那具体如何层序遍历我再上一题也详细介绍过了&#…...

脱离束缚:数字化工厂中ARM控制器的革命性应用!
近年来,中国数字经济体系已进入高速增长阶段。制造业作为中国经济高质量发展的重要支撑力量,在面临生产成本不断上涨、关键装备和核心零部件“受制于人”等挑战时,建设数字化工厂已成必然。 数字化工厂数据采集出现的问题 在数字工厂的建设…...
queue ide is not exists in YARN
报错内容: 2023-08-17 17:30:31.342 [ERROR] [BaseTaskScheduler-Thread-7 ] o.a.l.o.s.a.AsyncExecTaskRunnerImpl (79) [run] - Failed to execute task astJob_1_codeExec_1 org.apache.linkis.orchestrator.ecm.exception.ECMPluginErrorException: errCode:…...

【C++】UDP通信:客户端向服务端发送消息并接收服务端回应的消息
目录 1 UDP简介 2 通信 3 实践 4 运行结果 1 UDP简介 (1)UDP通信是无连接的,因此不需要connect操作。 (2)UDP通信过程需要指定数据接收端的IP和端口。 (3)UDP不对收到的数据进行排序。 (4)UDP对接收到的数据报不回复确认信息。 (5)如果发生了数据丢失,不会丢一…...
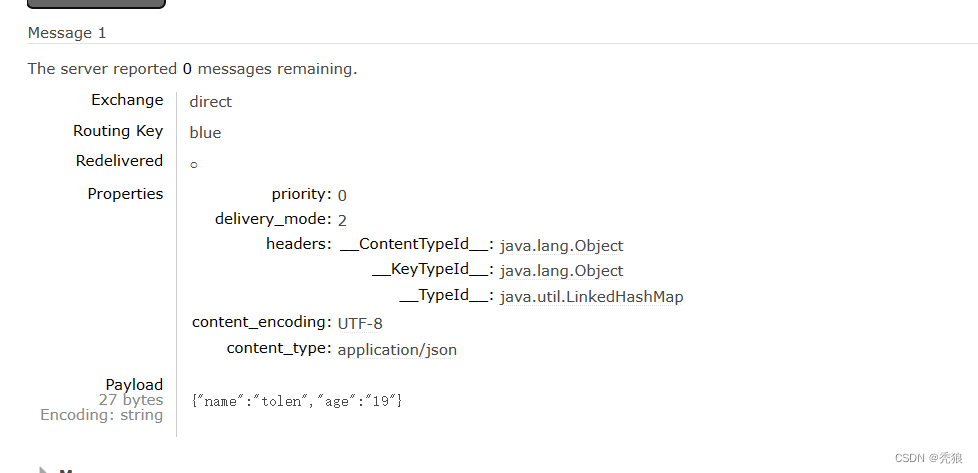
RabbitMq深度学习
什么是RabbitMq? RabbitMQ是一个开源的消息队列中间件,它实现了高级消息队列协议(AMQP)。它被广泛用于分布式系统中的消息传递和异步通信。RabbitMQ提供了一种可靠的、可扩展的机制来传递消息,使不同的应用程序能够相互之间进行…...
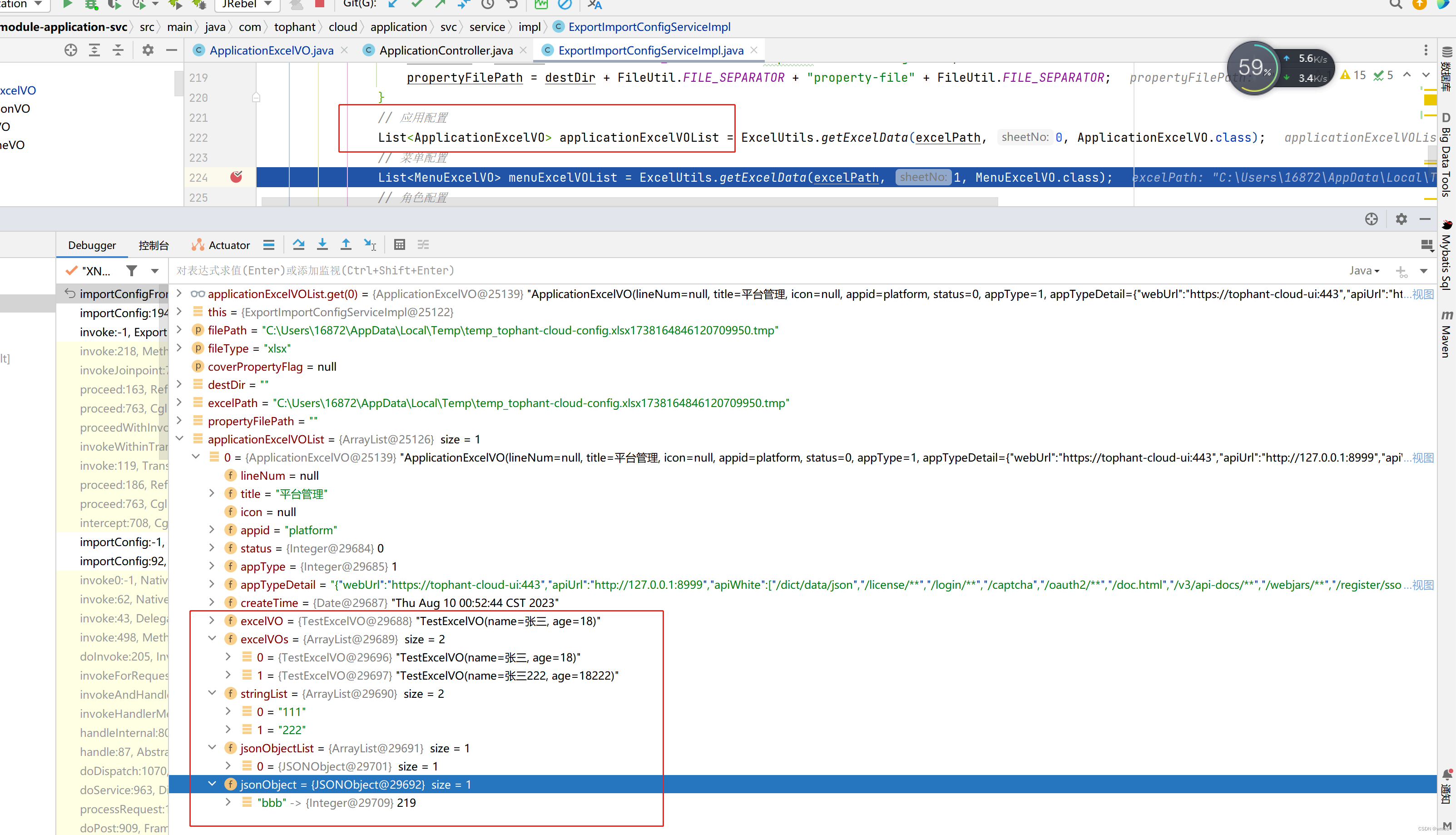
EasyExcel自定义字段对象转换器支持转换实体和集合实体
文章目录 1. 实现ObjectConverter2. 使用3. 测试3.1 导出excel3.2 导入excel 1. 实现ObjectConverter package com.tophant.cloud.common.excel.converters;import cn.hutool.json.JSONUtil; import com.alibaba.excel.converters.Converter; import com.alibaba.excel.enums.…...
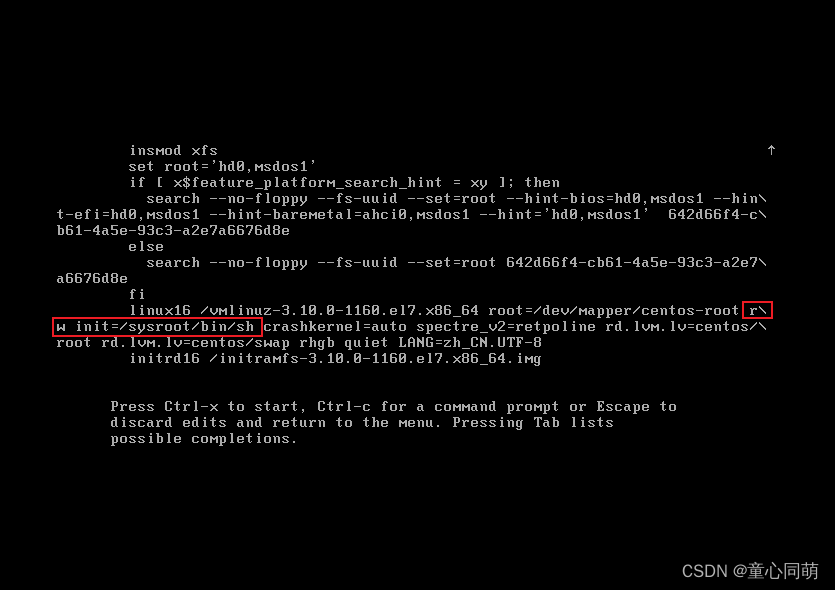
Linux重置ROOT密码(CentOS)
解释说明 在CentOS中重置root密码通常需要进入单用户模式,这是一个没有密码限制的特殊模式,允许您以root权限登录系统并更改密码。 重启系统 如果您无法登录到系统,可以通过重启系统来开始这个过程。您可以使用虚拟机控制台、物理服务器控制台…...

【Spring】一文带你彻底搞懂IOC、AOP
目录 首先简单了解一下什么是spring框架 什么是IOC? 什么是依赖注入(DI)? 控制反转和依赖注入又有什么关系? AOP是什么? SpringAOP的实现 说了这么多抽象概念,举个实例方便理解 首先简单…...
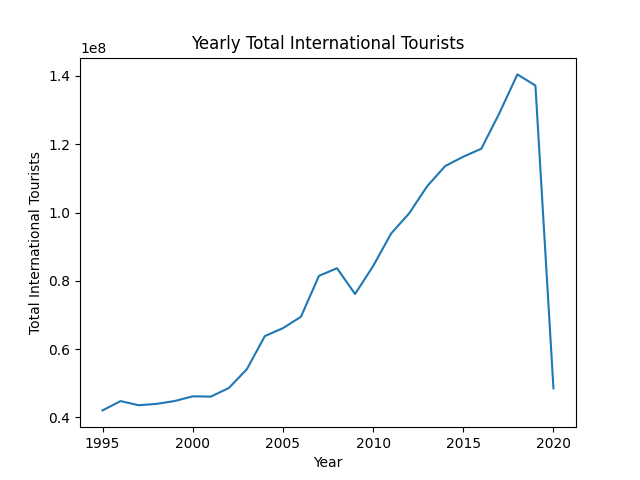
国际旅游网络的大数据分析(数学建模练习题)
题目:国际旅游网络的大数据分析 伴随着大数据时代的到来,数据分析已经深入到现代社会生活中的各个方面。 无论是国家政府部门、企事业单位还是个人,数据分析工作都是进行决策之前的 重要环节。 山东省应用统计学会是在省民政厅注册的学术类社会组织&…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

【版本控制】GitHub Desktop 入门教程与开源协作全流程解析
目录 0 引言1 GitHub Desktop 入门教程1.1 安装与基础配置1.2 核心功能使用指南仓库管理日常开发流程分支管理 2 GitHub 开源协作流程详解2.1 Fork & Pull Request 模型2.2 完整协作流程步骤步骤 1: Fork(创建个人副本)步骤 2: Clone(克隆…...
