数学建模-模型详解(2)
微分模型
当谈到微分模型时,通常指的是使用微分方程来描述某个系统的动态行为。微分方程是描述变量之间变化率的数学方程。微分模型可以用于解决各种实际问题,例如物理学、工程学、生物学等领域。
微分模型可以分为两类:常微分方程和偏微分方程。常微分方程描述的是只有一个自变量的函数的导数,而偏微分方程描述的是多个自变量的函数的导数。
常微分方程的一些常见类型包括:一阶线性常微分方程、一阶非线性常微分方程、高阶线性常微分方程等。偏微分方程的一些常见类型包括:热传导方程、波动方程、扩散方程等。





Logistic 模型
对下列人口数据:
# %%import numpy as np
import pandas as pd
from scipy.optimize import curve_fit# %%# 源数据
df = pd.DataFrame({'year': [1790, 1800, 1810, 1820, 1830, 1840, 1850, 1860, 1870],'population': [3.9, 5.3, 7.2, 9.6, 12.9, 17.1, 23.2, 31.4, 38.6],
})x0 = float(df['population'][0])
t0 = float(df['year'][0])# %%# Logistic 模型
def x(t, r, xm):return xm / (1 + (xm/x0-1)*np.exp(-r*(t-t0)))# 拟合参数
popt, pcov = curve_fit(x,df['year'].tolist(),df['population'].tolist(),bounds=((0, 1), (.1, np.inf)))
r, xm = popt[0], popt[1]
print('r =', r)
print('xm =', xm)# 预测 1900 人口
print('population in 1900 =', x(1900, r, xm))# %%# 画出预测曲线
import matplotlib.pyplot as pltyear = np.linspace(1790,2000,21)
population = []
for each in year:population.append(x(each,r,xm))
plt.scatter(df['year'], df['population'], label='actual')
plt.plot(year, population, label='predict', color='coral')
plt.legend()
得到 r = 0.032 , x m = 159.3 r=0.032,x_m=159.3r=0.032,x =159.3,并预测 1900 年人口为 73.09 73.0973.09,得到预测曲线。
Python 代码
微分方程求解
求微分方程:
# %%import numpy as np
from scipy.integrate import odeint
from sympy import *# %%# 使用 scipy 求数值解
# 微分方程
dy = lambda y,x:-2*y + x**2 + 2*x# 数值范围
x1 = np.linspace(1,10,20)# 求数值解,y 的初始值为 2
y1 = odeint(dy, 2, x1)
y1# %%# 使用 sympy 求解析解# 定义变量和函数
x = symbols('x', real=True)
y = Function('y')# 定义方程和约束
eq = y(x).diff(x) + 2*y(x) - x**2 - 2*x
con = {y(1): 2,
}# 求解
f = simplify(dsolve(eq, ics=con))
f# %%# 向解中代入不同的值
x2 = np.linspace(1,10,100)
y2 = []
for each in x2:y2.append(list(sorted(f.subs(x,each).evalf().atoms()))[1])# %%# 画图
import matplotlib.pyplot as pltplt.scatter(x1,y1, label='x1', color='coral')
plt.plot(x2,y2, label='x2')
plt.legend()
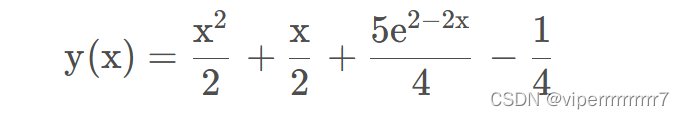
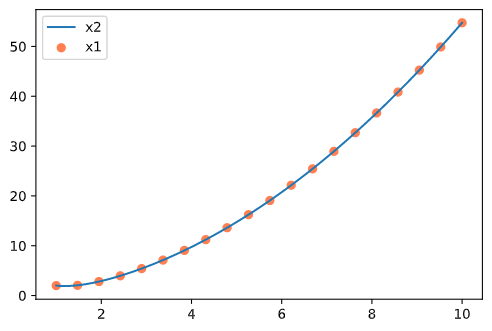
得到解析解的公式,以及数值解 x 1 和解析解的曲线 x 2 ,发现数值解和解析解大致吻合。
相关文章:

数学建模-模型详解(2)
微分模型 当谈到微分模型时,通常指的是使用微分方程来描述某个系统的动态行为。微分方程是描述变量之间变化率的数学方程。微分模型可以用于解决各种实际问题,例如物理学、工程学、生物学等领域。 微分模型可以分为两类:常微分方程和偏微分…...
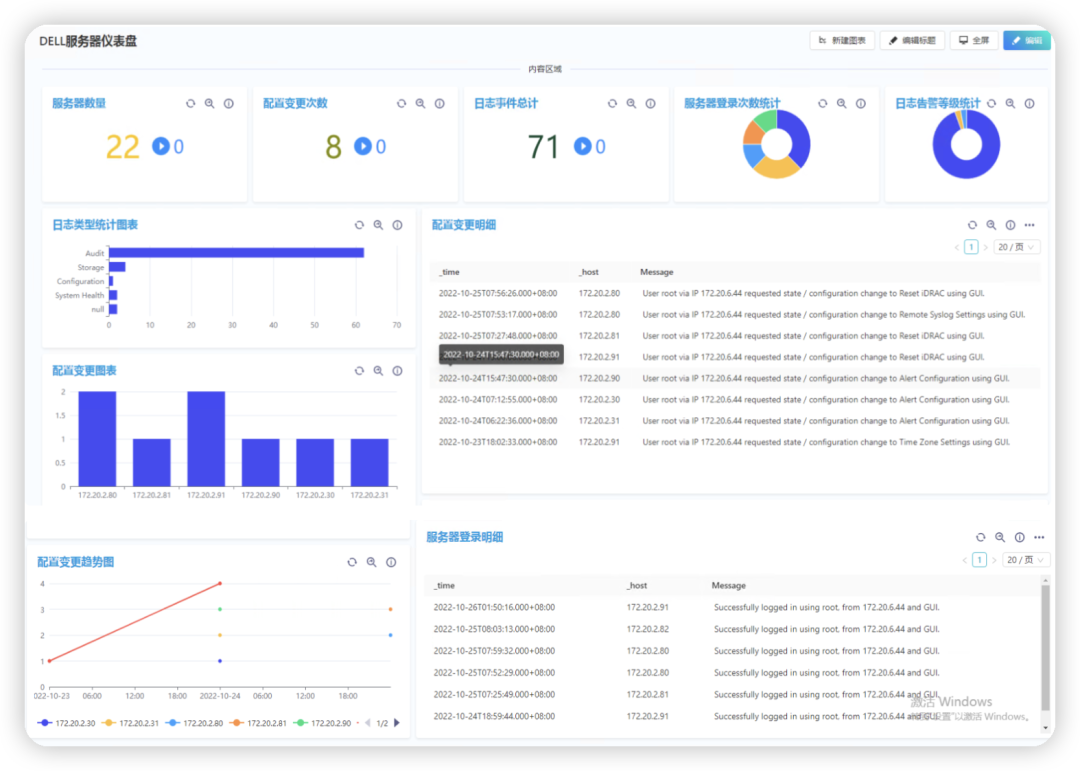
IT运维:使用数据分析平台监控DELL服务器
概述 在企业日常运维中,我们有着大量的服务器设备,设备故障一般可以通过常用的监控软件实现自动告警,但如果在管理运维中我们要做的不仅仅是发现故障,处理硬件故障,我们还需要进一步的了解,今年一共出现了多…...
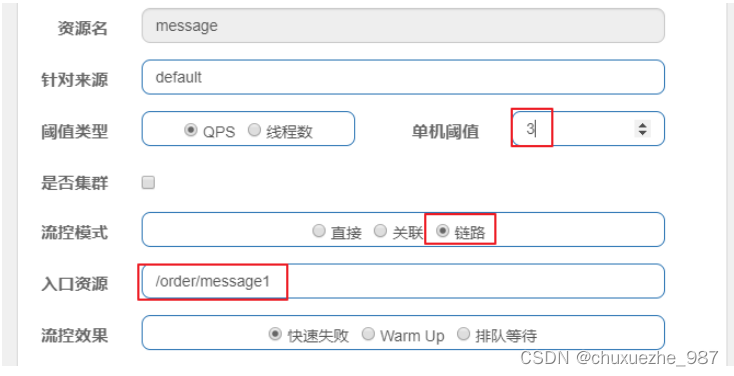
Spring Cloud Alibaba-Sentinel规则
1 流控规则 流量控制,其原理是监控应用流量的QPS(每秒查询率) 或并发线程数等指标,当达到指定的阈值时 对流量进行控制,以避免被瞬时的流量高峰冲垮,从而保障应用的高可用性。 第1步: 点击簇点链路,我们就可以看到访…...

go http-proxy
我们这里主要讲使用HTTP/1.1协议中的CONNECT方法建立起来的隧道连接,实现的HTTP Proxy。这种代理的好处就是不用知道客户端请求的数据,只需要原封不动的转发就可以了,对于处理HTTPS的请求就非常方便了,不用解析他的内容…...
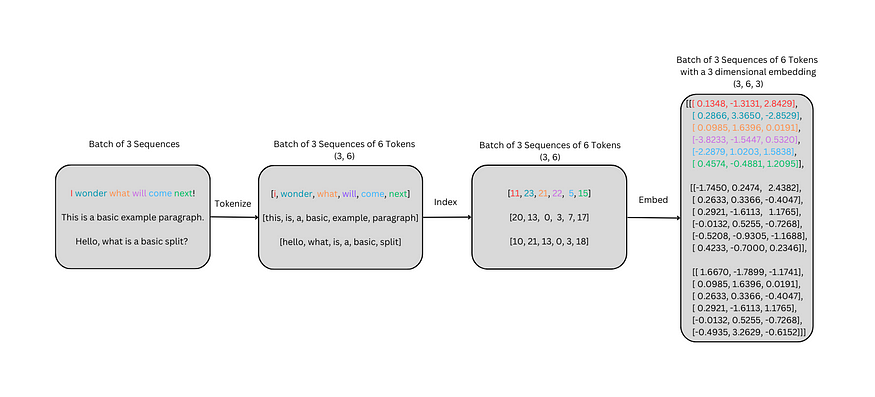
用变压器实现德-英语言翻译【01/8】:嵌入层
一、说明 本文是“用变压器实现德-英语言翻译”系列的第一篇文章。它引入了小规模的嵌入来建立感知系统。接下来是嵌入层的变压器使用。下面简要概述了每种方法,然后是德语到英语的翻译。 二、技术背景 嵌入层的目标是使模型能够详细了解单词、标记或其他输入之间的…...

【vue3.0中ref与reactive的区别及使用】
什么是ref与reactive ref与reactive都是Vue3.0中新增的API,用于响应式数据的处理。 1. ref ref是一个函数,可以用于将一个普通的数据类型转换成响应式数据。ref返回一个包含value属性的对象,通过修改value属性的值,可以触发组件…...
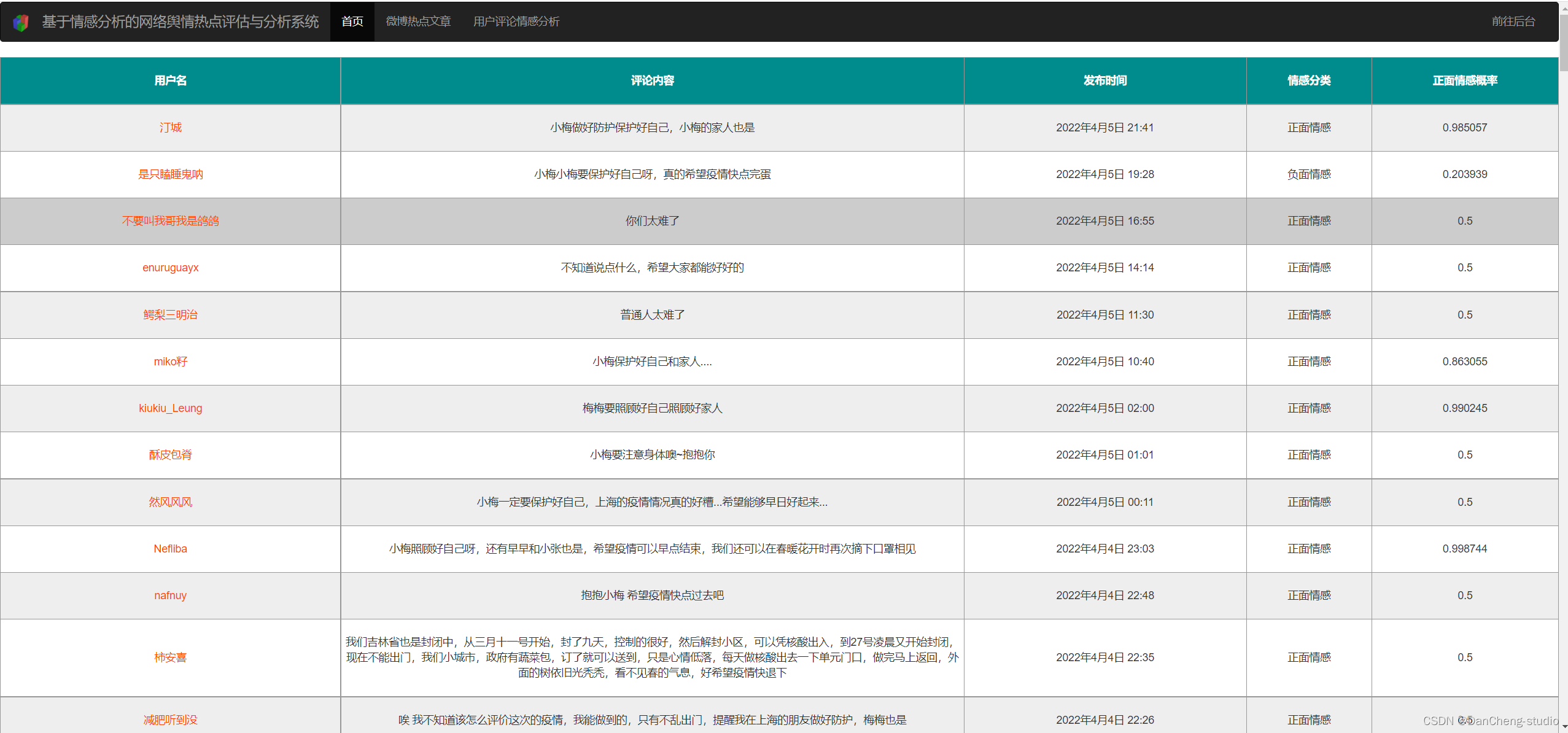
计算机竞赛 基于情感分析的网络舆情热点分析系统
文章目录 0 前言1 课题背景2 数据处理3 文本情感分析3.1 情感分析-词库搭建3.2 文本情感分析实现3.3 建立情感倾向性分析模型 4 数据可视化工具4.1 django框架介绍4.2 ECharts 5 Django使用echarts进行可视化展示5.1 修改setting.py连接mysql数据库5.2 导入数据5.3 使用echarts…...

C++ 动态分配内存|动态数组
int** arr new int* [n]; for (int i 0; i < n; i) {arr[i] new int[2]; } 以上代码是用C动态分配了一个二维数组arr,其中arr是一个指向int指针的指针,n是一个整数。代码的目的是创建一个包含n个大小为2的整数数组的二维数组。 首先,…...

React Diff算法原理
文章目录 前言Diff算法原理 前言 👉点此(想要了解Diff算法) Diff算法原理 React Diff算法是React用于更新虚拟DOM树的一种算法。它通过比较新旧虚拟DOM树的差异,然后只对有差异的部分进行更新,从而提高性能。 Reac…...
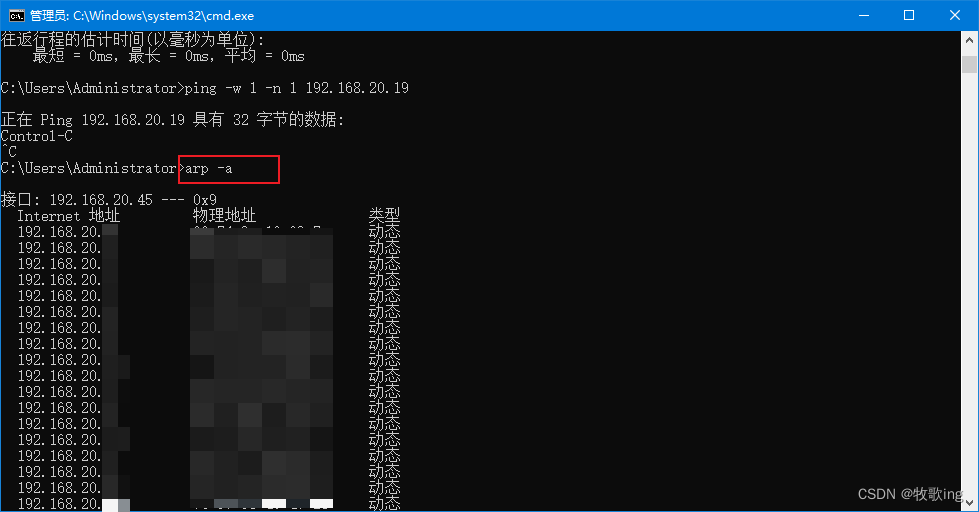
查局域网所有占用IP
查局域网所有占用IP 按:winr 出现下面界面,在文本框中输入 cmd 按确定即可出现cmd命令界面 在cmd命令窗口输入你想要ping的网段,下面192.168.20.%i即为你想要ping的网段,%i代表0-255 for /L %i IN (1,1,254) DO ping -w 1 -n 1…...

【MySQL】引擎类型
与其他DBMS一样,MySQL有一个 具体管理和处理数据的内部引擎 。在使用create table语句时,该引擎具体创建表,而在使用select或进行其他数据库处理时,该引擎在内部处理你的请求。多数时候,引擎都隐藏在DBMS内࿰…...

springMVC之HttpMessageConverter
文章目录 前言一、RequestBody二、RequestEntity三、ResponseBody四、SpringMVC处理json五、SpringMVC处理ajax六、RestController注解七、ResponseEntity总结 前言 HttpMessageConverter,报文信息转换器,将请求报文转换为Java对象,或将Java…...

计算机网络aaaaaaa
差错检测 在一段时间内,传输错误的比特占所传输比特总数的比率称为误码率BER(Bit Error Rate) 11111111111111111111111111111111111111111111111111111111111111111111111111111111 11111111111111111111111111111111111111111111111111111111111111111111111111…...
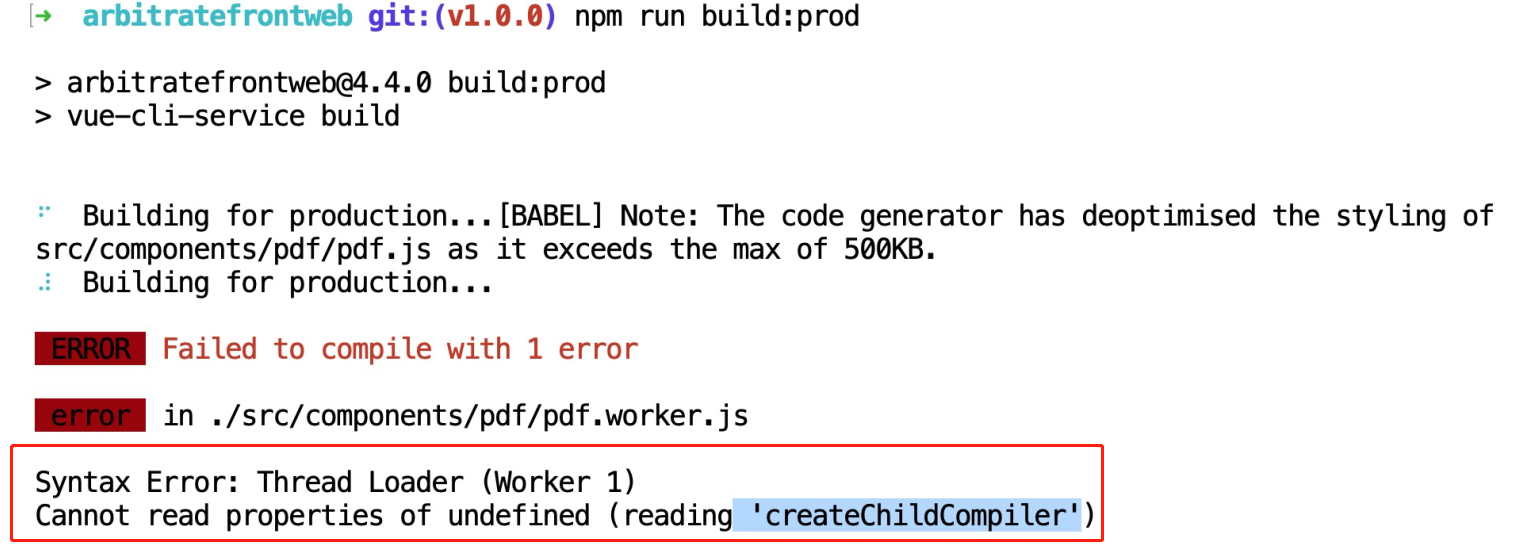
pdf.js构建时,报Cannot read property ‘createChildCompiler‘ of undefined #177的解决方法
在本地和CI工具进行构建时,报如下错误。 Cannot read property createChildCompiler of undefined #177解决方法: 找到vue.config.js,在 module.exports {parallel: false, //新增的一行chainWebpack(config) {....config.module.rule(&…...

Spring Boot(Vue3+ElementPlus+Axios+MyBatisPlus+Spring Boot 前后端分离)【六】
😀前言 本篇博文是关于Spring Boot(Vue3ElementPlusAxiosMyBatisPlusSpring Boot 前后端分离)【六】,希望你能够喜欢 🏠个人主页:晨犀主页 🧑个人简介:大家好,我是晨犀,希望我的文章…...

idea配置注释模板
一、类的模板 设置里面依次找到图中标注的地方 填入 /** ${describe} author 填入你的名字 date ${YEAR}-${MONTH}-${DAY} ${TIME} version 1.0.0 */配置完成后,新创建的类就会自动生成类开头的注释 二、方法的注释模板 如图创建模板 步骤6中填入 *** $descrip…...

Unity编辑器扩展:提高效率与创造力的关键
Unity编辑器扩展:提高效率与创造力的关键 前言 一、理解Unity编辑器二、扩展Unity编辑器的意义三、扩展Unity编辑器的必要性四、Unity编辑器的扩展方式五、扩展Unity编辑器的步骤六、Unity编辑器扩展的应用案例七、总结 前言 Unity是一款广泛使用的游戏开发引擎&am…...

Java之对象引用实践
功能概述 从JDK1.2版本开始,程序可以通过4种类型的对象的引用来管控对象的生命周期。这4种引用分别为,强引用、软引用、弱引用和虚引用。本文中针对各种引用做了相关测试,并做对应分析。 功能实践 场景1:弱引用、虚引用、软引用…...
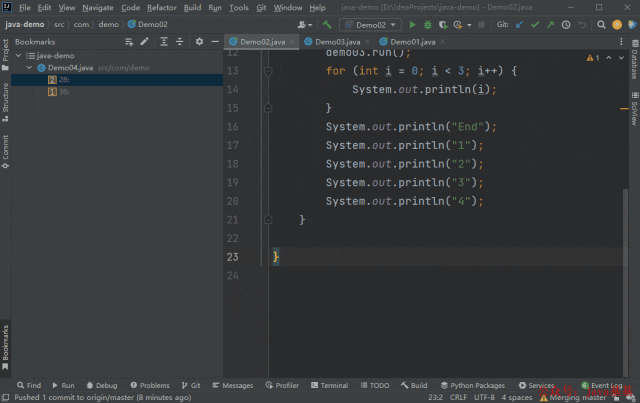
IntelliJ IDEA快捷键大全 + 动图演示!
来自:https://mp.weixin.qq.com/s/434xV02QkDiAFC1yFCAtZw 一、构建/编译 二、文本编辑 三、光标操作 四、文本选择 五、代码折叠 六、多个插入符号和范围选择 七、辅助编码 八、上下文导航 九、查找操作 十、符号导航 十一、代码分析 十二、运行和调试 …...
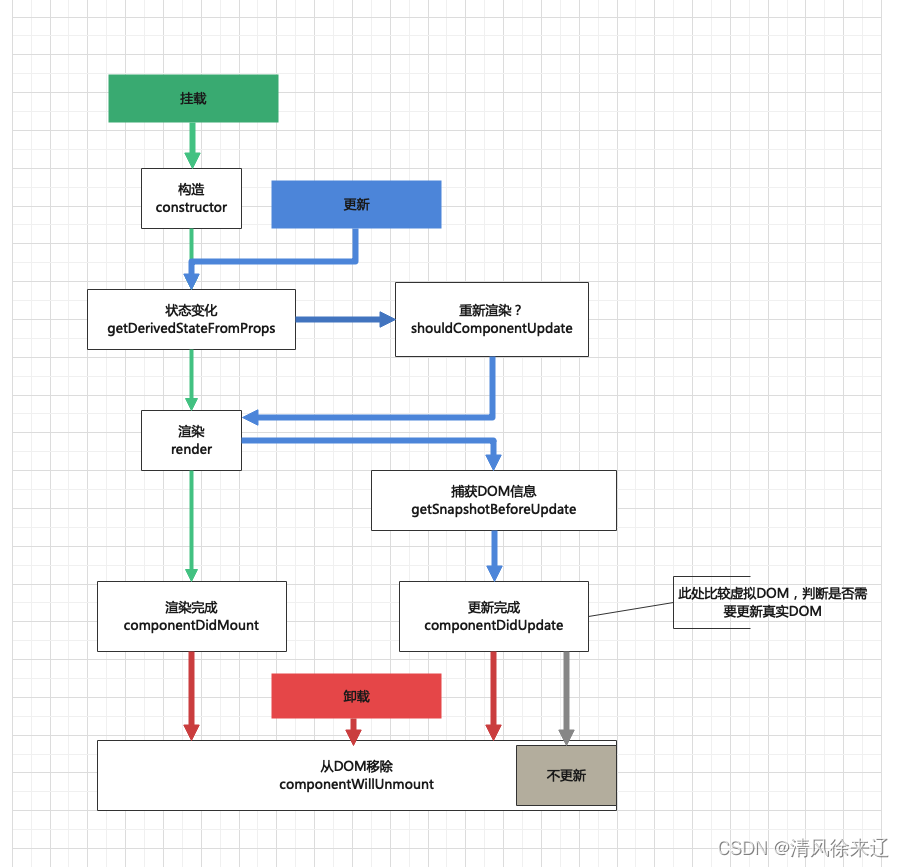
React 生命周期
React的生命周期 一、什么是React的生命周期二、传统生命周期2.1、挂载(Mounting)2.2、更新(Updating)2.3、卸载(Unmounting)2.4、API2.4.1、render2.4.1.1、Updating 阶段,render调用完还有可能…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

字符串哈希+KMP
P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...

react菜单,动态绑定点击事件,菜单分离出去单独的js文件,Ant框架
1、菜单文件treeTop.js // 顶部菜单 import { AppstoreOutlined, SettingOutlined } from ant-design/icons; // 定义菜单项数据 const treeTop [{label: Docker管理,key: 1,icon: <AppstoreOutlined />,url:"/docker/index"},{label: 权限管理,key: 2,icon:…...

【多线程初阶】单例模式 指令重排序问题
文章目录 1.单例模式1)饿汉模式2)懒汉模式①.单线程版本②.多线程版本 2.分析单例模式里的线程安全问题1)饿汉模式2)懒汉模式懒汉模式是如何出现线程安全问题的 3.解决问题进一步优化加锁导致的执行效率优化预防内存可见性问题 4.解决指令重排序问题 1.单例模式 单例模式确保某…...

