JavaScript刷LeetCode拿offer-树的遍历
什么是树
- 一种
分层数据的抽象模型。 - 前端工作中常见的树包括:DOM树,级联选择,树形控件
- JS中没有树,可以用Object和Array构建树
- 树的常用操作:
深度/广度优先遍历,先中后序遍历
深度优先遍历
- 访问
根节点 - 对根节点的
children挨个进行深度优先遍历
代码展示:
const tree = {val: 'a',children: [{val: 'b',children: [{val: 'd',children: []},{val: 'e',children: []}]},{val: 'c',children: [{val: 'f',children: []},{val: 'g',children: []}]}],
};const dfs = (root) => {console.log(root.val);root.children.forEach(dfs);
}dfs(tree);
输出顺序:a -> b -> d -> e -> c -> f -> g
广度优先遍历
- 新建一个
队列,把根节点入队 - 把
队头出队并访问 - 把
队头的children分别入队 - 重复二,三步,直到队列为空
代码展示:
const bfs = (root) => {const q = [root];while (q.length) {const n = q.shift();console.log(n.val);n.children.forEach((child) => {q.push(child);})}
}bfs(tree);
输出顺序:a -> b -> c -> d -> e -> f -> g
先序遍历
- 访问
根节点 - 对根节点的
左子树进行先序遍历 - 对根节点的
右子树进行先序遍历
代码展示:
const bt = {val: 1,left: {val: 2,left: {val: 4,left: null,right: null},right: {val: 5,left: null,right: null}},right: {val: 3,left: {val: 6,left: null,right: null},right: {val: 7,left: null,right: null}}
};
// 递归
const preorder = (root) => {if (!root) return;console.log(root.val);preorder(root.left);preorder(root.right);
}preorder(tree);// 迭代
const preorder = (root) => {if (root) return;const stack = [root];while (stack.length) {const n = stack.pop();console.log(top.val);if (n.right) stack.push(n.right);if (n.left) stack.push(n.left);}}
}preorder(tree);
参考视频:传送门
输出顺序:1 -> 2 -> 4 -> 5 -> 3 -> 6 -> 7
中序遍历
- 对根节点的
左子树进行中序遍历 - 访问
根节点 - 对根节点的
右子树进行中序遍历
代码展示:
// 递归
const inorder = (root) => {if (!root) return;preorder(root.left);console.log(root.val);preorder(root.right);
}inorder(tree);// 迭代
const inorder = (root) => {if (!root) return;const stack = [];let p = root;while (stack.length || p) {while (p) {stack.push(p);p = p.left;}const n = stack.pop();console.log(n.val);p = n.right;}
}inorder(tree);
输出顺序:4 -> 2 -> 5 -> 1 -> 6 -> 3 -> 7
后序遍历
- 对根节点的
左子树进行后序遍历 - 对根节点的
右子树进行后序遍历 - 访问
根节点
代码展示:
// 递归
const postorder = (root) => {if (!root) return;preorder(root.left);preorder(root.right);console.log(root.val);
}postorder(tree);// 迭代
const postorder = (root) => {if (!root) return;const stack = [root];const outputStack = [];while (stack.length) {const n = stack.pop();outputStack.push(n);if (n.left) stack.push(n.left);if (n.right) stack.push(n.right);}while (outputStack) {const n = outputStack.pop();console.log(n.val);}
}postorder(tree);
输出顺序:4 -> 5 -> 2 -> 6 -> 7 -> 3 -> 1
leetcode题目
难度:简单
- 二叉树的最大深度
思路:
- 求最大深度,优先考虑
深度优先遍历 - 在深度优先遍历过程中,
记录每个节点所在的层级,找到最大的层级即可
代码展示:
/*** @param {TreeNode} root* @return {number}*/
var maxDepth = function(root) {let maxDepth = 0;const dfs = (n, l) => {if (!n) return;dfs(n.left, l + 1);dfs(n.right, l + 1);if (!n.left && !n.right) maxDepth = Math.max(maxDepth, l);}dfs(root, 1);return maxDepth;
};
复杂度分析:
-
时间复杂度:O(n):n为二叉树节点个数。
-
空间复杂度:O(height):height为二叉树的最大深度。在平均情况下,二叉树的高度与节点个数为对数关系,即 O(logN)。而在最坏情况下,树形成链状,空间复杂度为 O(N)。
- 翻转二叉树
思路:
- 方法一使用
广度优先遍历,在遍历树的过程中,交换当前层级下的左右子树 - 方法二使用
递归解决,递归最重要的是定义子问题。
代码展示:
方法一:广度优先遍历
/*** @param {TreeNode} root* @return {TreeNode}*/
var invertTree = function(root) {if (!root) root;const bfs = (root) => {const q = [root];while (q.length) {const n = q.shift();const temp = n.right;n.right = n.left;n.left = temp;if (n.left) q.push(n.left);if (n.right) q.push(n.right);}}bfs(root);return root;
}
方法二:递归
/*** @param {TreeNode} root* @return {TreeNode}*/
var invertTree = function(root) {if (!root) return null;let newTree = new TreeNode(root.val);newTree.left = invertTree(root.right);newTree.right = invertTree(root.left);return newTree;
};
复杂度分析:
-
时间复杂度:O(n):n为二叉树节点个数。
-
空间复杂度:O(height):height为二叉树的最大深度。在平均情况下,二叉树的高度与节点个数为对数关系,即 O(logN)。而在最坏情况下,树形成链状,空间复杂度为 O(N)。
- 对称二叉树
思路:
- 通过遍历比较两个相同根节点的左子树和右子树的值是否相等
- 如果每次都相等,直到两个节点都不存在,说明是对称的
- 如果两个节点不相等,则说明不对称
代码展示:
/** * @param {TreeNode} root * @return {boolean} */
var isSymmetric = function(root) {if (!root) return false;const checkSym = (p, q) => {if (!p && !q) return true;if (!p || !q) return false;return p.val === q.val && checkSym(p.left, q.right) && checkSym(q.left, p.right);}return checkSym(root, root);
}
复杂度分析:
-
时间复杂度:O(n):n为二叉树节点数。
-
空间复杂度:O(n):n为二叉树节点数,最差情况为O(n)。
- 二叉树的直径
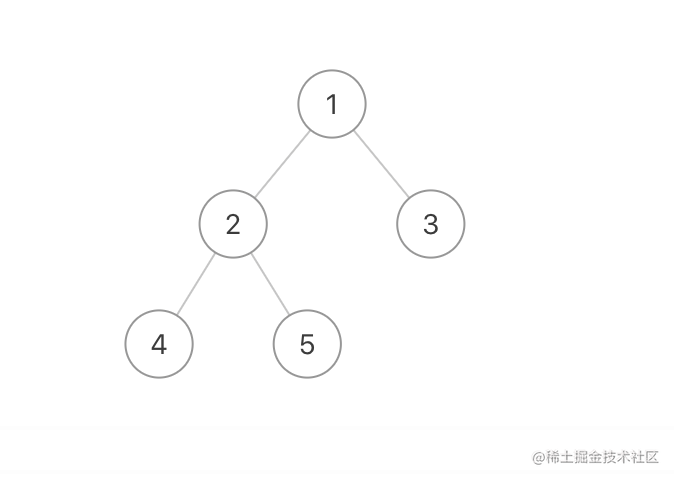
思路:
- 考虑
深度优先遍历 - 寻找两个最深的节点距离之和
代码展示:
/*** @param {TreeNode} root* @return {number}*/
var diameterOfBinaryTree = function(root) {if (!root) return 0;let res = 1; // 默认为根节点的路径长度const dfs = (root) => {if (!root) return 0;let L = dfs(root.left); // 左子树深度,上图为例,最长L为2let R = dfs(root.right); // 右子树深度,上图为例,最长R为1res = Math.max(res, L + R + 1); // 最大L+R+1,+1为根节点,总共深度为4,即节点树为4return Math.max(L, R) + 1; // 包含根节点的深度,上图为例,最长L为2,最长R为1}dfs(root);return res - 1; // 最终结果要得到直径为3
};
复杂度分析:
- 时间复杂度:O(n):n为二叉树节点数。
- 空间复杂度:O(height):height为二叉树的最大深度。在平均情况下,二叉树的高度与节点个数为对数关系,即 O(logN)。而在最坏情况下,树形成链状,空间复杂度为 O(N)。
剑指 Offer 27. 二叉树的镜像
思路:
- 逐层递归互换左右子树节点的位置
代码展示:
/*** @param {TreeNode} root* @return {TreeNode}*/
var mirrorTree = function(root) {if (!root) return root;const temp = root.left;root.left = root.right;root.right = temp;mirrorTree(root.left);mirrorTree(root.right);return root;
}
优化后:
/** * @param {TreeNode} root * @return {TreeNode} */
var mirrorTree = function(root) {if (!root) return root;[root.left, root.right] = [mirrorTree(root.right), mirrorTree(root.left)];return root;
}
复杂度分析:
-
时间复杂度:O(n):n为二叉树节点数。
-
空间复杂度:O(n):n为二叉树节点树。
- 二叉树的最近公共祖先
剑指 Offer 68 - II. 二叉树的最近公共祖先
思路:
- 递归
代码展示:
/** * @param {TreeNode} root * @param {TreeNode} p * @param {TreeNode} q * @return {TreeNode} */
var lowestCommonAncestor = function(root, p, q) {// 当传入递归的树等于 p 或者等于 q,说明找到了 p 或者 q,返回给递归调用的 l 或 rif (!root || p === root || q === root) return root;let l = lowestCommonAncestor(root.left, p, q); // 递归调用,寻找 p 和 qlet r = lowestCommonAncestor(root.right, p, q); // 递归调用,寻找 p 和 qreturn l && r ? root : l || r; // 如果 p 和 q 分别在 root.left 和 root.right 中找到,则根节点 root 成为最近的公共祖先返回。// 假如 p 和 q 在 root.left 中找到,递归会把 p 和 q 的公共祖先返回给 l。// 假如,p 和 q 在 root.right 中找到,递归会把 p 和 q 的公共祖先返回给 r。// 根节点root,l 或 r 最终成为当前函数的返回值。
};
复杂度分析:
- 时间复杂度:O(n):n为二叉树节点数。
- 空间复杂度:O(n):n为二叉树节点数。递归调用的栈深度取决于二叉树的高度,二叉树最坏情况下为一条链,此时高度为 N,因此空间复杂度为 O(N)。
剑指 Offer 55 - I. 二叉树的深度
思路:
- 考虑
深度优先遍历
代码展示:
var maxDepth = function (root) {if (!root) return 0;let max = 0;const dfs = (root, l) => {if (root.left) dfs(root.left, l + 1);if (root.right) dfs(root.right, l + 1);if (!root.left && !root.right) max = Math.max(max, l);}dfs(root, 1);return max;
}
复杂度分析:
-
时间复杂度:O(n):n为二叉树节点数,计算树的深度需要遍历所有节点。
-
空间复杂度:O(n):最差情况下,空间复杂度为O(n)。
- 二叉树的所有路径
思路:
- 本题考虑使用
深度优先遍历。 - 如果当前节点有
左子树或右子树,就递归调用函数,直到左右子树都不存在,此时就是我们要找的的路径。
代码展示:
/*** @param {TreeNode} root* @return {string[]}*/
var binaryTreePaths = function(root) {if (!root) return [];const res = [];const dfs = (root, path) => {if (root) {path += root.val;if (!root.left && !root.right) {res.push(path);} else {path += '->';dfs(root.left, path);dfs(root.right, path);}}}dfs(root, "");return res;
};
复杂度分析:
- 时间复杂度:O(n^2):n为二叉树节点数。在深度优先搜索中每个节点会被访问一次且只会被访问一次,每一次会对 path 变量进行拷贝构造,时间代价为 O(N),故时间复杂度为 O(N^2)。
- 空间复杂度:O(n^2):n为二叉树节点数。
剑指 Offer 32 - I. 从上到下打印二叉树
剑指 Offer 32 - II. 从上到下打印二叉树 II
- 解题方法同二叉树的层序遍历
- 平衡二叉树
思路:
-
考虑
深度优先遍历 -
算出最大深度和最小深度的差值,即可判断是否为平衡二叉树 (本题和求二叉树直径做法类似)
代码展示:
/*** @param {TreeNode} root* @return {boolean}*/
var isBalanced = function(root) {if (!root) return true;let diff = 0;const dfs = (root) => {if (!root) return 0;let L = dfs(root.left);let R = dfs(root.right);diff = Math.max(diff, Math.abs(R - L));return Math.max(L, R) + 1;}dfs(root);return diff - 1 <= 0;
};
复杂度分析:
-
时间复杂度:O(n):n为二叉树节点数。
-
空间复杂度:O(n):n为二叉树节点数,最差情况为O(n)。
- 合并二叉树
思路:
- 递归对两个相同位置的节点相加
代码展示:
/*** @param {TreeNode} root1* @param {TreeNode} root2* @return {TreeNode}*/
var mergeTrees = function(root1, root2) {if (!root1 || !root2) return root1 || root2;let newRoot = new TreeNode(root1.val + root2.val);newRoot.left = mergeTrees(root1.left, root2.left);newRoot.right = mergeTrees(root1.right, root2.right);return newRoot;
};
复杂度分析:
-
时间复杂度:O(n):n为二叉树节点数。
-
空间复杂度:O(n):n为二叉树节点数。
- 路径总和
思路:
- 考虑
深度优先遍历 - 记录从根节点到当前节点的和,与target比较。
代码展示:
/** * @param {TreeNode} root * @param {number} targetSum * @return {boolean} */
var hasPathSum = function(root, targetSum) {if (!root) return false;let res = false;const dfs = (root, val) => {if (root.left) dfs(root.left, val + root.left.val);if (root.right) dfs(root.right, val + root.right.val);if (!root.left && !root.right && val === targetSum) res = true;}dfs(root, root.val);return res;
};
复杂度分析:
-
时间复杂度:O(n):n为二叉树节点数。
-
空间复杂度:O(n):n为二叉树节点数。
- 二叉树的最小深度
思路:
-
方法一考虑使用
广度优先遍历 -
方法二考虑使用
深度优先遍历
代码展示:
方法一:
/*** @param {TreeNode} root* @return {number}*/
var minDepth = function(root) {if (!root) return 0;let minDep = Infinity;const bfs = (root, l) => {const q = [[root, l]];while (q.length) {const [n, l] = q.shift();if (n.left) q.push([n.left, l + 1]);if (n.right) q.push([n.right, l + 1]);if (!n.left && !n.right) minDep = Math.min(minDep, l);}}bfs(root, 1);return minDep;
};
方法二:
/** * @param {TreeNode} root * @return {number} */
var minDepth = function(root) {if (!root) return 0;if (root.left && root.right) {return 1 + Math.min(minDepth(root.left), minDepth(root.right));} else if (root.left) {return 1 + minDepth(root.left);} else if (root.right) {return 1 + minDepth(root.right);} else {return 1;}
};
复杂度分析:
-
时间复杂度:O(n):n为二叉树节点数。
-
空间复杂度:O(n):n为二叉树节点数。
- N 叉树的前序遍历
思路:
- 类似于二叉树的前序遍历
代码展示:
// 递归
var preorder = function(root) {if (!root) return [];const res = [];const preord = (n) => {if (n) res.push(n.val);n.children.forEach(preord);}preord(root);return res;
};// 迭代
var preorder = function(root) {if (!root) return [];const stack = [root];const res = [];while (stack.length) {const n = stack.pop();res.push(n.val);n.children.reverse().forEach(child => {stack.push(child);});}return res;
}
复杂度分析:
- 时间复杂度:O(n):n为二叉树节点数。
- 空间复杂度:O(height):height为二叉树最大深度。
剑指 Offer 54. 二叉搜索树的第k大节点
思路:
- 根据树的特点,采用
中序遍历,按右子树 - 根节点 - 左子树的顺序遍历,就可以由大到小找到第k大节点
代码展示:
/*** @param {TreeNode} root* @param {number} k* @return {number}*/
var kthLargest = function(root, k) {if (!root || k <= 0) return null;const stack = [];const res = null;let p = root;while (stack.length || p) {while (p) {stack.push(p);p = p.right;}const top = stack.pop();if (--k === 0) return top.val;p = top.left;}return res;
};
复杂度分析:
- 时间复杂度:O(n):n为二叉树节点数。
- 空间复杂度:O(n):n为二叉树节点数。
难度:中等
- 二叉树的前序遍历
代码展示:
/*** @param {TreeNode} root* @return {number[]}*/
var preorderTraversal = function(root) {if (!root) return [];const stack = [root];const res = [];while (stack.length) {const n = stack.pop();res.push(n.val);if (n.right) stack.push(n.right);if (n.left) stack.push(n.left);}return res;
};
复杂度分析:
-
时间复杂度:O(n):n为二叉树节点数。
-
空间复杂度:O(n)
- 二叉树的中序遍历
代码展示:
/*** @param {TreeNode} root* @return {number[]}*/
var inorderTraversal = function(root) {if (!root) return [];const stack = [];const res = [];let p = root;while (stack.length || p) {while (p) {stack.push(p);p = p.left;}const n = stack.pop();res.push(n.val);p = n.right;}return res;
};
复杂度分析:
-
时间复杂度:O(n):n为二叉树节点数。
-
空间复杂度:O(n)
- 二叉树的后序遍历
代码展示:
/*** @param {TreeNode} root* @return {number[]}*/
var postorderTraversal = function(root) {if (!root) return [];const stack = [root];const outputStack = [];const res = [];while (stack.length) {const n = stack.pop();outputStack.push(n);if (n.left) stack.push(n.left);if (n.right) stack.push(n.right);}while (outputStack.length) {const n = outputStack.pop();res.push(n.val);}return res;
};
复杂度分析:
-
时间复杂度:O(n):n为二叉树节点数。
-
空间复杂度:O(n)
- 二叉树的层序遍历
代码展示:
方法一:深度优先遍历
/*** @param {TreeNode} root* @return {number[][]}*/
var levelOrder = function(root) {if (!root) return [];const res = [];const dfs = ([root, l]) => {if (!res[l]) {res[l] = [root.val];} else {res[l].push(root.val)}if (root.left) dfs([root.left, l + 1]);if (root.right) dfs([root.right, l + 1]);}dfs([root, 0]);return res;
};
方法二:广度优先遍历
/*** @param {TreeNode} root* @return {number[][]}*/
var levelOrder = function(root) {if (!root) return [];let res = [];const bfs = (root, l) => {const q = [[root, l]];while (q.length) {const [n, l] = q.shift();if (!res[l]) res[l] = [];res[l].push(n.val);if (n.left) q.push([n.left, l + 1]);if (n.right) q.push([n.right, l + 1]);}};bfs(root, 0);return res;
};
复杂度分析:
-
时间复杂度:O(n):n为二叉树节点数。
-
空间复杂度:O(n)
-
从前序与中序遍历序列构造二叉树
-
从中序与后序遍历序列构造二叉树
剑指 Offer 07. 重建二叉树
思路:
- 递归
代码展示:
参考:多种解法,逐渐优化
/*** @param {number[]} preorder* @param {number[]} inorder* @return {TreeNode}*/
var buildTree = function(preorder, inorder) {if (!preorder.length || !inorder.length) return null;const map = new Map();for (let i = 0; i < inorder.length; i++) {map.set(inorder[i], i);}const builder = (p_start, p_end, i_start, i_end) => {if (p_start > p_end) return null;let rootVal = preorder[p_start]; // 找到根节点let root = new TreeNode(rootVal); // 设置二叉树的根节点let mid = map.get(rootVal); // 找到根节点在inorder中的位置let leftNum = mid - i_start; // 左子树的个数root.left = builder(p_start + 1, p_start + leftNum, i_start, mid - 1);root.right = builder(p_start + leftNum + 1, p_end, mid + 1, i_end);return root;}return builder(0, preorder.length - 1, 0, inorder.length - 1);
};
复杂度分析:
-
时间复杂度:O(n):n为二叉树节点数。
-
空间复杂度:O(n)
- 二叉树的锯齿形层序遍历
思路:
- 同二叉树层序遍历
代码展示:
/*** @param {TreeNode} root* @return {number[][]}*/
var zigzagLevelOrder = function(root) {if (!root) return [];const res = [];const bfs = ([root, index]) => {if (!root) return;if (!res[index]) {res[index] = [root.val];} else {index % 2 === 0 ? res[index].push(root.val) : res[index].unshift(root.val);}if (root.left) bfs([root.left, index + 1]);if (root.right) bfs([root.right, index + 1]);}bfs([root, 0]);return res;
};
复杂度分析:
-
时间复杂度:O(n):n为二叉树节点数。
-
空间复杂度:O(n)
- 二叉树的右视图
思路:
-
方法一考虑
广度优先遍历,每层保留最后一个元素 -
方法二考虑使用类似
先序遍历,根 - 右 - 左的方式遍历,每层第一个出现的元素保留下来即可
代码展示:
方法一:广度优先遍历
/*** @param {TreeNode} root* @return {number[]}*/
var rightSideView = function(root) {if (!root) return [];const res = [];const bfs = (root, l) => {const q = [[root, l]]while (q.length) {const [n, l] = q.shift();res[l] = n.val;if (n.left) q.push([n.left, l + 1]);if (n.right) q.push([n.right, l + 1]);}}bfs(root, 0);return res;
};
方法二:
/*** @param {TreeNode} root* @return {number[]}*/
var rightSideView = function(root) {if (!root) return [];const res = [];const stack = [[root, 0]];while (stack.length) {const [n, l] = stack.pop();if (res[l] == undefined) res.push(n.val);if (n.left) stack.push([n.left, l + 1]);if (n.right) stack.push([n.right, l + 1]);}return res;
};
复杂度分析:
- 时间复杂度:O(n):n为二叉树节点数。
- 空间复杂度:O(n)
剑指 Offer 26. 树的子结构
思路:
- 递归比较
代码展示:
/** * @param {TreeNode} A * @param {TreeNode} B * @return {boolean} */
var isSubStructure = function(A, B) {if (!A || !B) return false;const isSameSub = (p, q) => {if (!q) return true;if (!p) return false;if (p.val !== q.val) return false;return isSameSub(p.left, q.left) && isSameSub(p.right, q.right);}return isSameSub(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B);
};
复杂度分析:
-
时间复杂度:O(mn):m,n分别为A和B的节点数。
-
空间复杂度:O(m)
- 验证二叉搜索树
代码展示:
/** * @param {TreeNode} root * @return {boolean} */
var isValidBST = function(root) {const helper = (root, lower, upper) => {if (root === null) {return true;}if (root.val <= lower || root.val >= upper) {return false;}return helper(root.left, lower, root.val) && helper(root.right, root.val, upper);}return helper(root, -Infinity, Infinity);
};
复杂度分析:
-
时间复杂度:O(n):n为二叉树节点数。
-
空间复杂度:O(n)
- 不同的二叉搜索树
思路:
- 卡塔兰数公式
代码展示:
var numTrees = function(n) {let C = 1;for (let i = 0; i < n; ++i) {C = C * 2 * (2 * i + 1) / (i + 2);}return C;
};
复杂度分析:
-
时间复杂度:O(n):n为二叉树节点数。
-
空间复杂度:O(1)
- 完全二叉树的节点个数
代码展示:
/** * @param {TreeNode} root * @return {number} */
var countNodes = function(root) {return root ? countNodes(root.left) + countNodes(root.right) + 1 : 0;
};
复杂度分析:
- 时间复杂度:O(n):n为二叉树节点数。
- 空间复杂度:O(1)
剑指 Offer 34. 二叉树中和为某一值的路径
代码展示:
/*** @param {TreeNode} root* @param {number} target* @return {number[][]}*/
var pathSum = function(root, target) {if (!root) return [];const res = [];let temp = [];const dfs = (root, v) => {if (!root) return null;temp.push(root.val);if (root.left) dfs(root.left, root.left.val + v);if (root.right) dfs(root.right, root.right.val + v);if (!root.left && !root.right && v === target) {res.push([...temp]);}temp.pop();}dfs(root, root.val);return res;
};
复杂度分析:
- 时间复杂度:O(n):n为二叉树节点数。
- 空间复杂度:O(n)
难度:困难
- 二叉树中的最大路径和
代码展示:
参考解法
/*** @param {TreeNode} root* @return {number}*/
var maxPathSum = function(root) {let maxNum = Number.MIN_SAFE_INTEGER;const dfs = (root) => {if (!root) return 0;const left = dfs(root.left);const right = dfs(root.right);const curMaxSum = left + root.val + right; // 当前子树内部最大路径和maxNum = Math.max(maxNum, curMaxSum);const outputMaxSum = root.val + Math.max(left, right); // 当前子树对上一层输出的最大路径和return outputMaxSum > 0 ? outputMaxSum : 0; // 大于0有输出的必要,小于0就返回0};dfs(root);return maxNum;
}
复杂度分析:
- 时间复杂度:O(n):n为二叉树节点数。
- 空间复杂度:O(n)
剑指 Offer 37. 序列化二叉树
总结
继续对树的深度/广度优先遍历,先中后序遍历,层序遍历等遍历和递归的方法,有更深入的理解和学习。
相关文章:

JavaScript刷LeetCode拿offer-树的遍历
什么是树 一种分层数据的抽象模型。前端工作中常见的树包括:DOM树,级联选择,树形控件JS中没有树,可以用Object和Array构建树树的常用操作:深度/广度优先遍历,先中后序遍历 深度优先遍历 访问根节点对根节…...

《FPGA学习》->呼吸灯
🍎与其担心未来,不如现在好好努力。在这条路上,只有奋斗才能给你安全感。你若努力,全世界都会为你让路。呼吸灯,简而言之就像人类呼吸一样,有节奏的让LED灯从:灭->微微亮->微亮->亮-&g…...
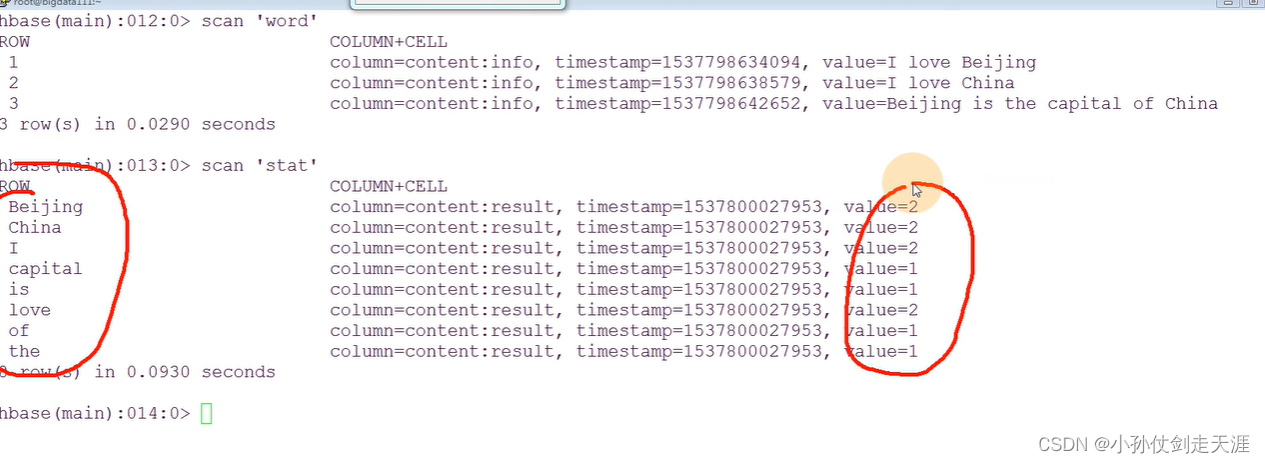
【大数据离线开发】7.4 HBase数据保存和过滤器
7.4 数据保存的过程 注意:数据的存储,都需要注意Region的分裂 HDFS:数据的平衡 ——> 数据的移动(拷贝)HBase:数据越来越多 ——> Region的分裂 ——> 数据的移动(拷贝) …...
CentOS7安装MariaDB步骤
文章目录1.配置MariaDB yum源2.安装MariaDBMariaDB数据库管理系统是MySQL的一个分支,主要由开源社区在维护,采用GPL授权许可。 MariaDB的目的是完全兼容MySQL,包括API和命令行,使之能轻松成为MySQL的代替品。 CentOS 6 或早期的版…...

软件测试13个最容易犯的错误
目录 一、 输入框测试 二、 搜索功能测试 三、 添加/修改功能 四、 删除功能 五、 上传图片功能测试 六、 查询结果列表 七、 返回键检查 八、 回车键检查 九、 刷新键检查 十、 直接URL链接检查(盗链问题) 十一、并发问题 十二、 业务流程测…...
)
华为OD机试真题Java实现【5键键盘的输出】真题+解题思路+代码(20222023)
🔥系列专栏 华为OD机试(Python)真题目录汇总华为OD机试(JAVA)真题目录汇总华为OD机试(C++)真题目录汇总华为OD机试(JavaScript)真题目录汇总文章目录 🔥系列专栏题目输入输出描述:示例1:示例2:解题思路代码实现运行结果:版权说明:题目...
化解射频和微波设计挑战的六个技巧
即使是最自信的设计人员,对于射频电路也往往望而却步,因为它会带来巨大的设计挑战,并且需要专业的设计和分析工具。这里将为您介绍六条技巧,来帮助您简化任何射频PCB 设计任务和减轻工作压力! 1、保持完好、精确的射频…...
)
linux内核—进程调度(核心)
目录 核心函数__schedule() 处理过程 1、选择下一个进程 2、切换线程 1)切换进程的虚拟地址空间 2)切换寄存器 3)执行清理工作 核心函数__schedule() 主要的调度程序 进入次函数的主要方法是: 1、显示阻塞:互…...
【STM32笔记】__WFI();进入不了休眠的可能原因(系统定时器SysTick一直产生中断)
【STM32笔记】__WFI();进入不了休眠的可能原因(系统定时器SysTick一直产生中断) 【STM32笔记】低功耗模式配置及避坑汇总 前文: blog.csdn.net/weixin_53403301/article/details/128216064 【STM32笔记】HAL库低功耗模式配置&am…...
【期末复习】例题讲解Dijkstra算法
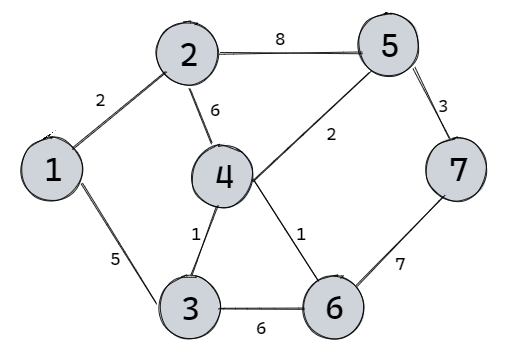
使用场景Dijkstra算法用于解决单源点最短路径问题,即给一个顶点作为源点,依次求它到图中其他n-1个顶点的最短距离。例题讲解Dijkstra算法将图中所有顶点分成两部分,第一部分是已知到源点最短距离的顶点Known(K),第二部分是不知道到…...

Pytorch 基础之张量索引
本次将介绍一下 Tensor 张量常用的索引与切片的方法: 1. index 索引 index 索引值表示相应维度值的对应索引 a torch.rand(4, 3, 28, 28) print(a[0].shape) # 返回维度一的第 0 索引 tensor print(a[0, 0].shape) # 返回维度一 0 索引位置…...
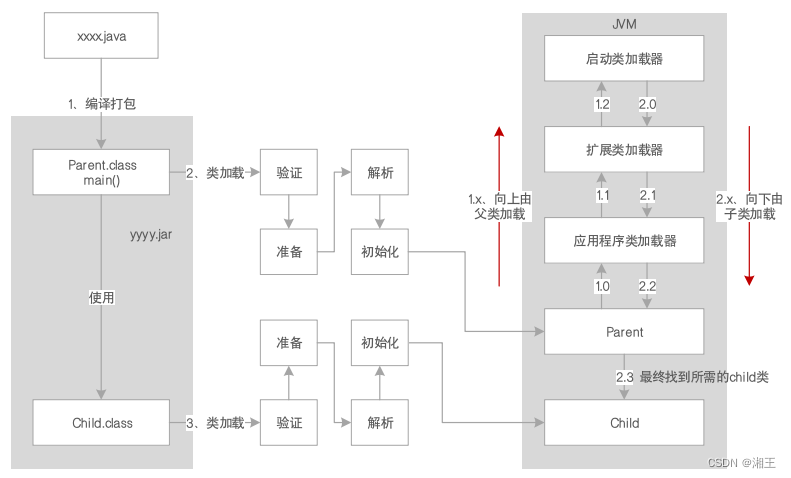
JVM系统优化实践(1):JVM概览
您好,我是湘王,这是我的CSDN博客,欢迎您来,欢迎您再来~这是多年之前做过的学习笔记,今天再翻出来,觉得仍然是记忆犹新。「独乐乐不如众乐乐」,就拿出来分享给「众乐乐」吧。目前大多…...

优秀!19年后,它再次成为TIOBE年度编程语言
新年伊始,TIOBE发布了2022年度编程语言,C时隔19年再度登顶,成为2022年最受欢迎的编程语言。TIOBE在2003年首次统计编程语言的流行指数时,C便成为年度编程语言。2022年,C获得了最高的人气4.62%,紧随其后的是…...
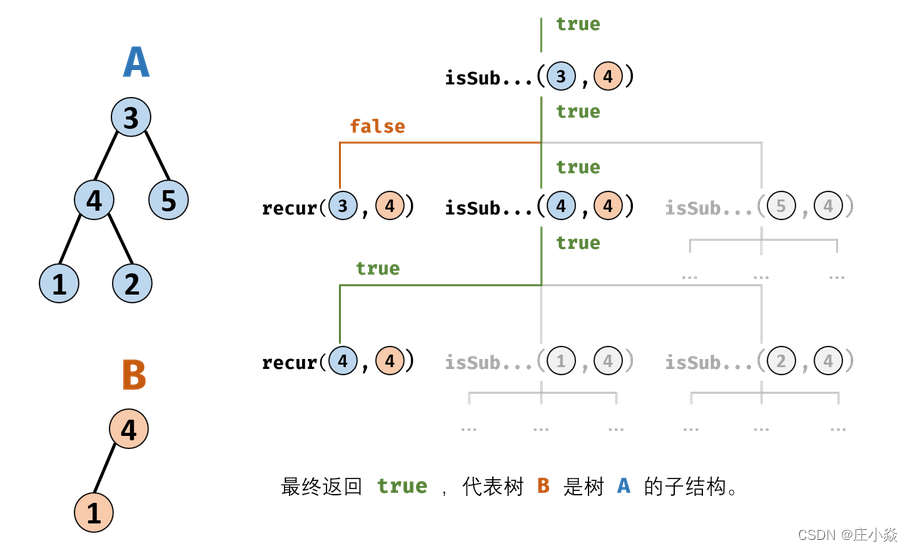
剑指 Offer 26. 树的子结构
摘要 剑指 Offer 26. 树的子结构 输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构),B是A的子结构, 即 A中有出现和B相同的结构和节点值。 一、子树解析 思路解析:若树B是树A的子结构,则…...

他是00年的,我们卷不过他...
现在的小年轻真的卷得过分了。前段时间我们公司来了个00年的,工作没两年,跳槽到我们公司起薪18K,都快接近我了。后来才知道人家是个卷王,从早干到晚就差搬张床到工位睡觉了。 最近和他聊了一次天,原来这位小老弟家里条…...

C#开发的OpenRA的OpenGL创建纹理流程
C#开发的OpenRA的OpenGL创建纹理流程 由于OpenRA采用的是OpenGL来显示游戏画面, 那么它就必然采用纹理来显示了。 并且由于它是2D的游戏,所以3D的模型是没有的,只要使用纹理贴图,就可以完全实现了游戏的功能。 OpenGL的纹理要起作用,需要经过一系列的动作。 先要使用glGen…...
3D目标检测(一)—— 基于Point-Based方法的PointNet系列
3D目标检测(一)—— PointNet,PointNet,PointNeXt, PointMLP 目录 3D目标检测(一)—— PointNet,PointNet,PointNeXt, PointMLP 前言 零、网络使用算法 …...

《设计模式》策略模式
策略模式 前言 先了解一下设计模式的几种类似: 行为型设计模式(Behavioral Design Pattern)是指一组设计模式,它们关注的是对象之间的通信和协作。行为型设计模式描述了对象之间的职责分配和算法的封装,以及如何在运…...

【离散数学】1. 数理逻辑
1.数理逻辑 2. 集合论 3. 代数系统 4. 图论 离散数学:研究离散量结构及相互关系的学科 数理逻辑集合论代数系统图论 逻辑:研究推理的科学 数学方法:引进一套符号系统的方法 数理逻辑是用数学方法研究形式逻辑的科学,即使用符号化…...
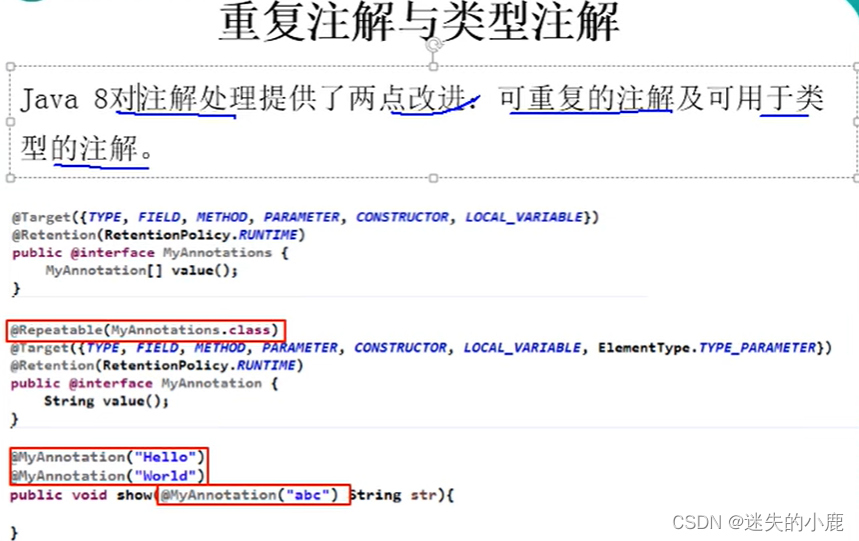
Java8新特性学习
Java8新特性学习为啥使用Lambda表达式Lambda表达式的基础语法无参无返回有参无返回一个参数多参单个语句体类型推断四大内置核心函数式接口其他接口方法引用与构造器引用Stream简介什么是StreamStream操作步骤创建Stream中间操作终止操作(终端操作)归约与收集并行流…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...
