C++--动态规划背包问题(1)
1. 【模板】01背包_牛客题霸_牛客网
你有一个背包,最多能容纳的体积是V。
现在有n个物品,第i个物品的体积为vivi ,价值为wiwi。
(1)求这个背包至多能装多大价值的物品?
(2)若背包恰好装满,求至多能装多大价值的物品?
输入描述:
第一行两个整数n和V,表示物品个数和背包体积。
接下来n行,每行两个数vivi和wiwi,表示第i个物品的体积和价值。
1≤n,V,vi,wi≤10001≤n,V,vi,wi≤1000
输出描述:
输出有两行,第一行输出第一问的答案,第二行输出第二问的答案,如果无解请输出0。
示例1
输入:
3 5 2 10 4 5 1 4输出:
14 9说明:
装第一个和第三个物品时总价值最大,但是装第二个和第三个物品可以使得背包恰好装满且总价值最大。示例2
输入:
3 8 12 6 11 8 6 8输出:
8 0说明:
装第三个物品时总价值最大但是不满,装满背包无解。
分析:对于背包问题,这道题十分重要,分析过程看下图:

#include <iostream>
#include <string.h>
#include <vector>
#include <stdio.h>
using namespace std;
const int V=1010;//体积
int n=0;
int v=0;
int num[V];//体积
int val[V];//价值
int main()
{cin>>n;cin>>v;for(int i=0;i<n;i++){ cin>>num[i]>>val[i];} int dp[V];//第一题memset(dp,0,sizeof dp);//初始化for(int i=1;i<=n;i++){for(int j=v;j>=num[i-1];j--){dp[j] = max(dp[j],dp[j - num[i-1]] + val[i-1]);}}cout<<dp[v]<<endl;//第二题memset(dp,0,sizeof dp);for(int j = 1; j <= v; j++)dp[j] = -1;for(int i=1;i<=n;i++){for(int j=v;j>=num[i-1];j--){if(dp[j - num[i-1]] != -1)dp[j] = max(dp[j],dp[j - num[i-1]] + val[i-1]);}}cout << (dp[v] == -1 ? 0 : dp[v]) << endl;return 0;
}2.分割等和子集 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
给你一个 只包含正整数 的 非空 数组
nums。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。示例 1:
输入:nums = [1,5,11,5] 输出:true 解释:数组可以分割成 [1, 5, 5] 和 [11] 。示例 2:
输入:nums = [1,2,3,5] 输出:false 解释:数组不能分割成两个元素和相等的子集。
分析:对于这道题而言,需要解决的问题是如何转化为背包问题,这道题要求分割数组,使两个子数组的大小相等,所以我们可以求出数组元素和,然后除以2,判断是否可以整除,如果不可以,则返回false;可以整除2则适用背包问题:
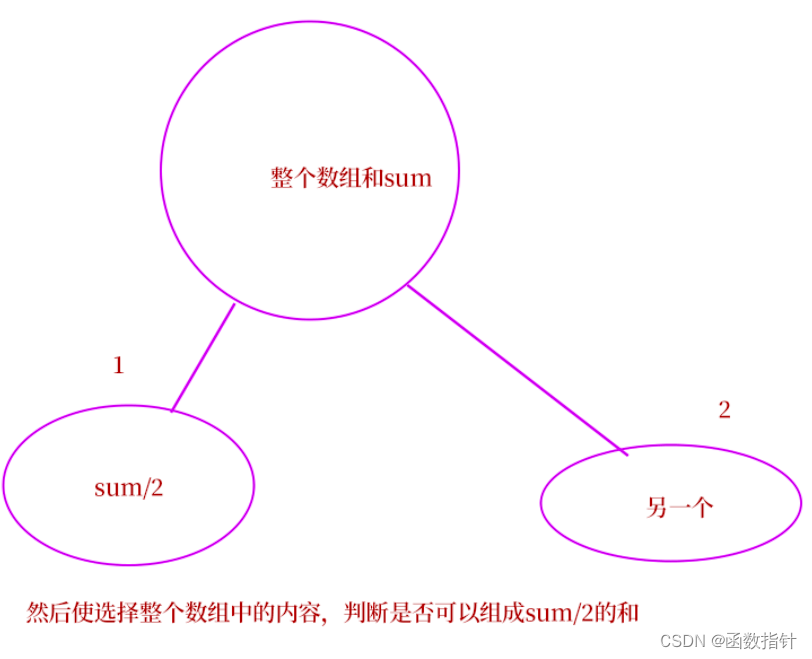
class Solution {
public:bool canPartition(vector<int>& nums) {int n=nums.size();int sum=0;for(const auto& s:nums) sum+=s;if(sum%2==1)return false;sum=sum/2;//初始化vector<bool> dp(sum+1);dp[0]=true;for(int i=1;i<=n;i++){for(int j=sum;j>=nums[i-1];j--){dp[j]=dp[j]||dp[j-nums[i-1]]; }}return dp[sum];}
};3.目标和 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
给你一个非负整数数组
nums和一个整数target。向数组中的每个整数前添加
'+'或'-',然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。返回可以通过上述方法构造的、运算结果等于
target的不同 表达式 的数目。示例 1:
输入:nums = [1,1,1,1,1], target = 3 输出:5 解释:一共有 5 种方法让最终目标和为 3 。 -1 + 1 + 1 + 1 + 1 = 3 +1 - 1 + 1 + 1 + 1 = 3 +1 + 1 - 1 + 1 + 1 = 3 +1 + 1 + 1 - 1 + 1 = 3 +1 + 1 + 1 + 1 - 1 = 3示例 2:
输入:nums = [1], target = 1 输出:1
分析:
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int sum=0;int n=nums.size();//转化为背包问题for(int i=0;i<n;i++) sum+=nums[i];if((sum+target)<0||(sum+target)%2) return 0;sum=(sum+target)/2;//初始化vector<int> dp(sum+1);dp[0]=1;for(int i=1;i<=n;i++){for(int j=sum;j>=nums[i-1];j--){dp[j]+=dp[j-nums[i-1]];}}return dp[sum];}
};4.最后一款石头的重量(2) 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
有一堆石头,用整数数组
stones表示。其中stones[i]表示第i块石头的重量。每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为
x和y,且x <= y。那么粉碎的可能结果如下:
- 如果
x == y,那么两块石头都会被完全粉碎;- 如果
x != y,那么重量为x的石头将会完全粉碎,而重量为y的石头新重量为y-x。最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回
0。示例 1:
输入:stones = [2,7,4,1,8,1] 输出:1 解释: 组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1], 组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1], 组合 2 和 1,得到 1,所以数组转化为 [1,1,1], 组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。示例 2:
输入:stones = [31,26,33,21,40] 输出:5
分析:
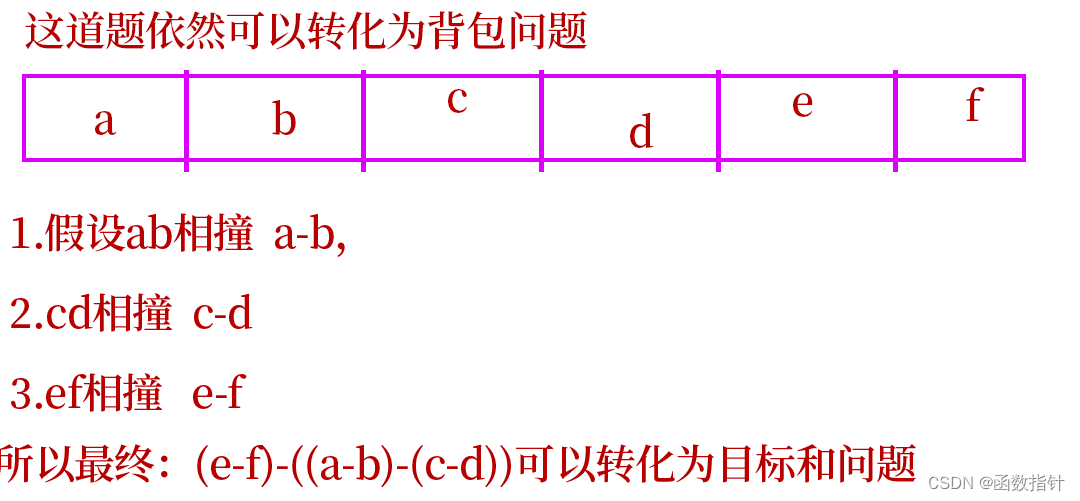
class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int sum=0;int n=stones.size();for(int i=0;i<n;i++) sum+=stones[i];int enquesum=sum;sum=sum/2;vector<int> dp(sum+1);for(int i=1;i<=n;i++){for(int j=sum;j>=stones[i-1];j--){dp[j]=max(dp[j],dp[j-stones[i-1]]+stones[i-1]);}}return enquesum-2*dp[sum];}
};相关文章:

C++--动态规划背包问题(1)
1. 【模板】01背包_牛客题霸_牛客网 你有一个背包,最多能容纳的体积是V。 现在有n个物品,第i个物品的体积为vivi ,价值为wiwi。 (1)求这个背包至多能装多大价值的物品? (2)若背包恰好装满&a…...
【Android-Flutter】我的Flutter开发之旅
目录: 0、文档:1、在Windows上搭建Flutter开发环境(1)[使用中国镜像(❌详细看官方文档)](https://docs.flutter.dev/community/china)(2)[下载最新版Flutter SDK(已包含Dart)](https://docs.flu…...
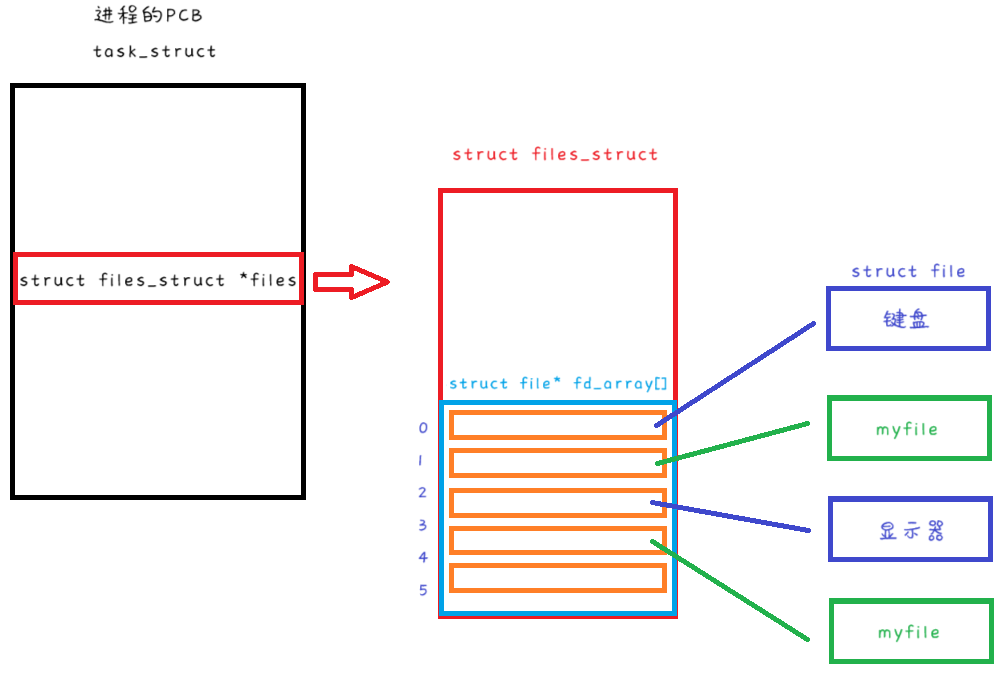
【Linux】深入理解文件操作
文章目录 初次谈论文件重温C语言文件操作系统文件操作接口openwriteread 再次谈论文件文件描述符文件描述符的分配规则 重定向什么是重定向重定向的本质系统调用接口实现重定向<、>、>> 初次谈论文件 开始之前先谈论一下关于文件的一些共识性问题。 一个文件可以…...
异地使用PLSQL远程连接访问Oracle数据库【内网穿透】
文章目录 前言1. 数据库搭建2. 内网穿透2.1 安装cpolar内网穿透2.2 创建隧道映射 3. 公网远程访问4. 配置固定TCP端口地址4.1 保留一个固定的公网TCP端口地址4.2 配置固定公网TCP端口地址4.3 测试使用固定TCP端口地址远程Oracle 前言 Oracle,是甲骨文公司的一款关系…...

【方案】基于AI边缘计算的智慧工地解决方案
一、方案背景 在工程项目管理中,工程施工现场涉及面广,多种元素交叉,状况较为复杂,如人员出入、机械运行、物料运输等。特别是传统的现场管理模式依赖于管理人员的现场巡查。当发现安全风险时,需要提前报告࿰…...

华为各型号交换机开启SNMP v3
设备型号:华为S5720S-28P-LI-AC 设备软件版本:V200R011C10SPC600 调试命令: snmp-agent snmp-agent sys-info version v3 snmp-agent group v3 GroupName privacy //{GroupName}是设置一个SNMP的组名,我设置是SNMPGroup snm…...

CocosCreator3.8研究笔记(一)windows环境安装配置
一、安装Cocos 编辑器 (1)、下载Cocos Dashboard安装文件 Cocos 官方网站Cocos Dashboard下载地址 : https://www.cocos.com/creator-download9下载完成后会得到CocosDashboard-v2.0.1-win-082215.exe 安装文件,双击安装即可。 …...

【JavaWeb 专题】15个最经典的JavaWeb面试题
文章目录 HTTP长连接和短连接HTTP/1.1 与 HTTP/1.0 的区别可扩展性缓存带宽优化长连接消息传递Host 头域错误提示 AjaxAjax 的优势: JSP 和 servlet 有什么区别?定义区别 JSP 的9大内置对象及作用JSP 的 4 种作用域?session 和 cookie 有什么…...
)
力扣:75. 颜色分类(Python3)
题目: 给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。 我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。 必须在不使用库内置的 sort …...
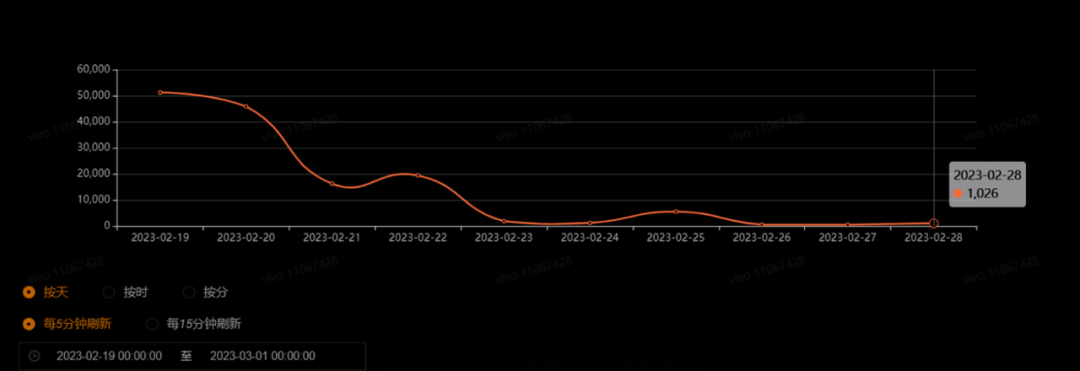
JVM 内存大对象监控和优化实践
作者:vivo 互联网服务器团队 - Liu Zhen、Ye Wenhao 服务器内存问题是影响应用程序性能和稳定性的重要因素之一,需要及时排查和优化。本文介绍了某核心服务内存问题排查与解决过程。首先在JVM与大对象优化上进行了有效的实践,其次在故障转移与…...

vue indexedDB 取指定数据库指定表 全部key用request.onsuccess
1 例子 export async function funcGetKey(dbName, tableName) {return new Promise((resolve, reject) > {// 打开指定的数据库const request indexedDB.open(dbName);request.onerror (event) > {console.error(打开数据库失败: , event.target.error);reject(event…...

Java 数据结构使用学习
Set和List的区别 Set 接口实例存储的是无序的,不重复的数据。List 接口实例存储的是有序的,可以重复的元素。 Set 检索效率低下,删除和插入效率高,插入和删除不会引起元素位置改变 <实现类有HashSet,TreeSet>。 List 和数…...
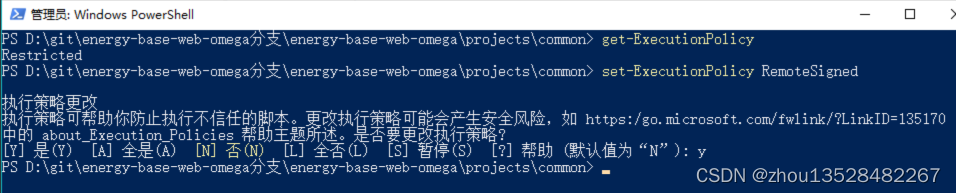
monorepo更新组件报错,提示“无法加载文件 C:\Program Files\nodejs\pnpm.ps1,因为在此系统上禁止运行脚本”
解决方法: 第一步:管理员身份运行 window.powershell, win x打开powerShell命令框,进入到对应项目路径。 第二步:执行:get-ExecutionPolicy,显示Restricted,表示状态是禁止的; 第…...

vue中html引入使用<%= BASE_URL %>变量
首先使用src相对路径引入 注意: js 文件放在public文件下 不要放在assets静态资源文件下 否则 可能会报错 GET http://192.168.0.113:8080/src/assets/js/websockets.js net::ERR_ABORTED 500 (Internal Server Error) 正确使用如下:eg // html中引…...

Android全面屏下,默认不会全屏显示,屏幕底部会留黑问题
前些天发现了一个蛮有意思的人工智能学习网站,8个字形容一下"通俗易懂,风趣幽默",感觉非常有意思,忍不住分享一下给大家。 👉点击跳转到教程 公司以前的老项目,便出现了这种情况,网上搜索了各种资料…...
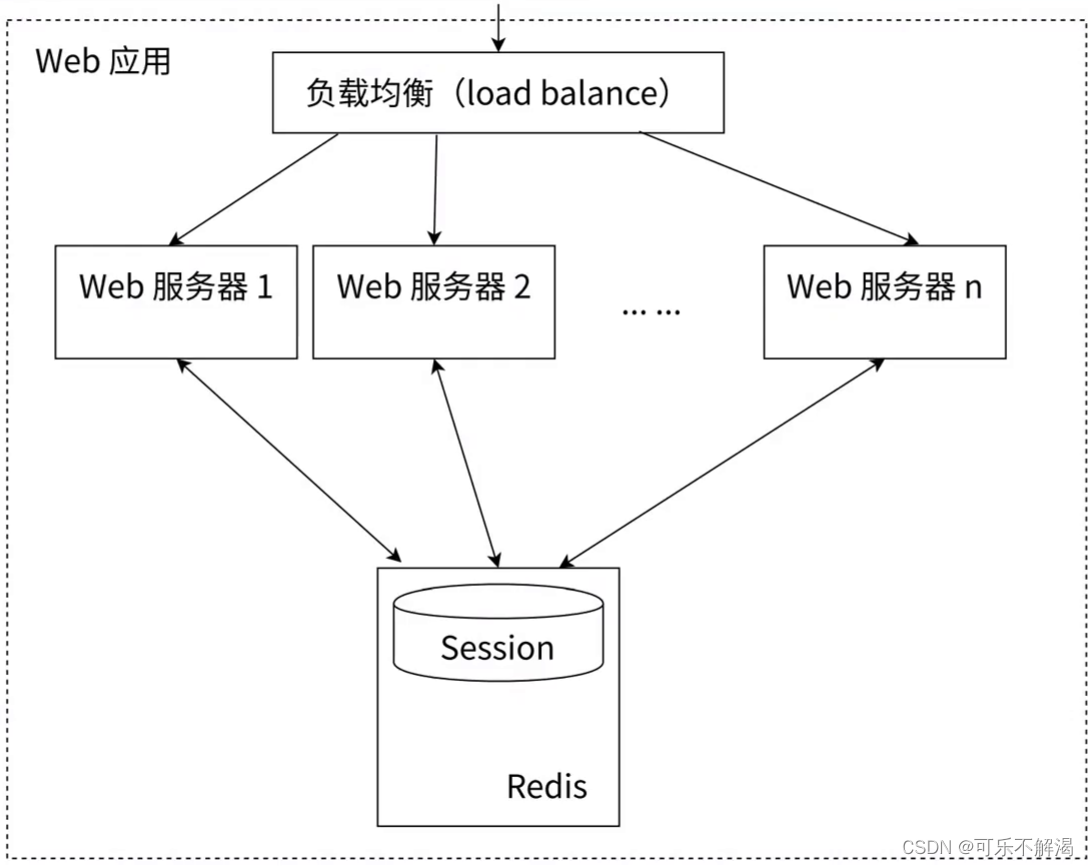
5.Redis-string
string 字符串 字符串类型是 Redis 最基础的数据类型,关于字符串需要特别注意: 1.⾸先Redis中所有 key 的类型都是字符串类型,⽽且其他⼏种数据结构也都是在字符串类似基础上构建的,例如 list 和 set 的元素类型是字符串类型。 2…...
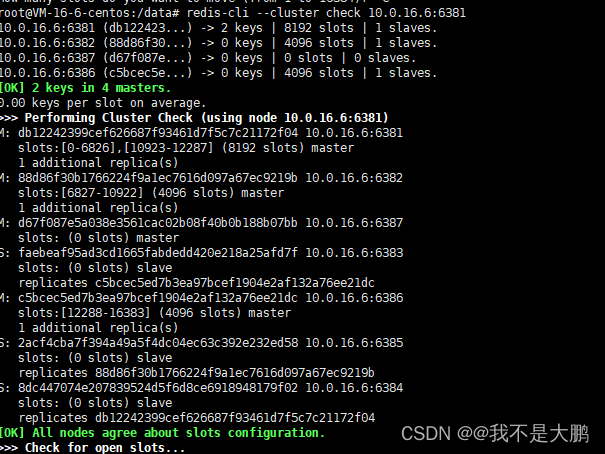
docker高级(redis集群三主三从)
1. 新建6个docker容器redis实例 docker run -d --name redis-node-1 --net host --privilegedtrue -v /redis/share/redis-node-1:/data redis:6.0.8 --cluster-enabled yes --appendonly yes --port 6381docker run -d --name redis-node-2 --net host --privilegedtrue -v /…...
linux 设置与命令基础(二)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、系统基本操作 二、命令类型 三、命令语法 四、命令补齐 五、命令帮助 六、系统基本操作命令 总结 前言 这是本人学习Linux的第二天,今天主…...

ubuntu20.04中ros2安装rosbridge及启动方式
ros2 启动rosbridge: 要启动ROS2中的rosbridge,需要先安装ROS2的rosbridge_suite软件包。使用以下命令安装: sudo apt-get update sudo apt-get install ros-<distro>-rosbridge-suite将<distro>替换为正在使用的ROS2发行版的名…...

TCP之超时重传、流量控制和拥塞控制
一、超时重传 TCP超时重传是TCP协议中的一种机制,用于在发生丢包或数据包未及时确认的情况下,重新发送未确认的数据段。 当发送方发送一个数据段后,会启动一个定时器(称为超时计时器),等待接收方的确认。…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...
