408数据结构考点总结
文章目录
- 第一章 绪论
- 考点 1:时间复杂度与空间复杂度
- 时间复杂度
- 空间复杂度
- 第二章 线性表
- 考点 2:顺序表
- 考点 3:单链表
- 第三章 栈和队列
- 考点 4:栈和队列的基本性质
- 考点5:循环队列
- 考点6:双端队列
- 输出受限的双端队列
- 输入受限的双端队列
- 考点7:栈与队列的应用
- 考点 8:特殊矩阵的存储
- 第四章 串
- 考点 9:串的模式匹配算法
- 第五章 树与二叉树
- 考点 10:树的基本性质
- 考点 11:特殊二叉树的定义与性质
- 特殊二叉树
- 完全二叉树的性质
- 考点 12:二叉树的遍历
- 考点 13:树、森林与二叉树的转换
- 考点 14:线索二叉树
- 考点 15:哈夫曼
- 哈夫曼树
- 哈夫曼编码
- 第六章 图
- 考点 16:图的基本概念
- 基本术语
- 图的基本性质
- 考点 17:图的存储及基本操作
- 邻接矩阵存储法
- 邻接表存储法
- 考点 18:图的遍历
- 广度优先搜索 BFS
- 深度优先搜索 DFS
- 考点 19:最小(代价)生成树
- Prim 算法
- Kruskal 算法
- 考点 20:最短路径
- 最短路径(权值)问题
- Dijkstra 算法
- Floyd 算法
- 考点 21:拓扑排序
- 考点 22:关键路径
- 求关键路径算法
- 第七章 查找
- 考点 23:查找的基本术语
- 考点 24:顺序查找
第一章 绪论
考点 1:时间复杂度与空间复杂度
时间复杂度
定义:将算法中基本运算的执行次数的数量级作为时间复杂度,记为O(n)O(n)O(n)。
计算原则
- 加法法则:T(n)=T1(n)+T2(n)=O(f(n))+O(g(n))=O(max(f(n),g(n)))T(n)=T_{1}(n)+T_{2}(n)=O(f(n))+O(g(n))=O(\max (f(n), g(n)))T(n)=T1(n)+T2(n)=O(f(n))+O(g(n))=O(max(f(n),g(n)))
- 乘法法则:T(n)=T1(n)T2(n)=O(f(n))O(g(n))=O(f(n)g(n))T(n)=T_{1}(n) T_{2}(n)=O(f(n)) O(g(n))=O(f(n) g(n))T(n)=T1(n)T2(n)=O(f(n))O(g(n))=O(f(n)g(n))
计算方法
- 列方程法:用于递推实现的算法中,设基本运算运行xxx次,找出与问题规模nnn之间的方程关系式,解出x=f(n)x=f\left ( n \right )x=f(n),f(n)f\left ( n \right )f(n)的最高次数为kkk,则算法的时间复杂度为O(nk)O\left ( n^{k} \right )O(nk)。
- 递推公式法:用于递归实现的算法中,设T(n)T\left ( n \right )T(n)是问题规模为nnn的算法的时间复杂度,T(n−1)T(n-1)T(n−1)是问题规模为n−1n-1n−1的算法的时间复杂度,建立T(n)T(n)T(n)与T(n−1)T(n-1)T(n−1)[或T(n−2)T(n-2)T(n−2)等]的递推关系式,根据关系式,解出T(n)T(n)T(n)。
空间复杂度
定义:指算法运行过程中所使用的辅助空间的大小,记为S(n)S(n)S(n)。算法原地工作是指算法所需辅助空间是常量,即O(1)O(1)O(1)。
递归算法特性:
- 一个算法直接或间接调用自身,称为递归调用。
- 必须有一个明确的递归结束条件,称为递归出口。
- 实现递归的关键是建立递归调用工作栈。栈的大小也就是递归深度和递归算法空间复杂度的。
第二章 线性表
考点 2:顺序表
定义:指用一组连续的存储单元,依次存储线性表中的各个元素,从而使得逻辑上相邻的元素在物理位置上也相邻,因此可以随机存取(根据首元素地址和元素序号)表中任何一个元素。
基本操作
-
结构
-
插入
若表长为nnn,下标从0开始,则在第iii位置插入元素eee,则从ana_nan到aia_iai都要向后移动一个位置,共需移动n−i+1n-i+1n−i+1个元素,平均时间复杂度为O(n)O(n)O(n)。
//判断1的范围是否有效,否则非法 //判断当前存储空间是否已满,否则不能插入 for(int j=L.length;j>=i;--) //将第1个位置及之后的元素后移L.data[j]=L.data[j-1]; L.data[i-1]=e; //在位置i处放入e,数组从0开始存储 L.length++; //线性表长度加1 -
删除
若表长为nnn,下标从000开始,当删除第i个元素时,则从i个元素时,则从i个元素时,则从ai+1a_{i+1}ai+1 到ana_nan都要向前移动一个位置,共需移动n−in-in−i个元素,平均时间复杂度为O(n)O(n)O(n)。
//判断1的范围是否有效 for(int j=i;j<L.length;j++) //将第i个位置及之后的元素前移L.data[j-1]=L.data[j]; L.length--; //线性表长度减1 -
查找
- 按序号(下标)查找:顺序表具有随机存取(根据首元地址和序号)的特点,时间复杂度为O(1)O(1)O(1)。
- 按值查找:主要运算是比较操作,比较的次数与值在表中的位置和表长有关,平均比较次数为(n+1)/2(n+1)/2(n+1)/2,时间复杂度为O(n)O(n)O(n)。
考点 3:单链表
定义:为了建立元素之间的线性关系,对每个链表结点,除了存放元素自身的信息,还需要存放一个指向其后继的指针。
基本操作
-
查找
只能从表中第一个结点出发顺序查找,顺着指针nextnextnext域逐个往下搜索,直到找到满足条件的结点为止。时间复杂度为O(n)O(n)O(n)。
-
创建
-
头插法:从一个空表开始,然后将新结点插入到当前链表的表头,即头结点之后。
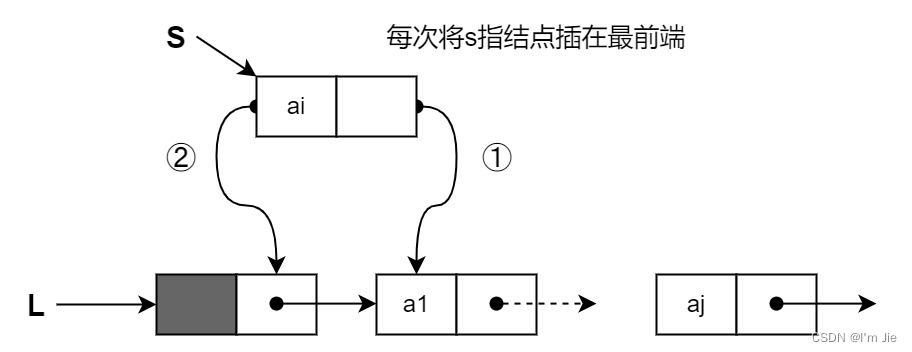
s->next=L->next; //①新结点的指针指向原链表的第一个结点 L->next=s; //②头结点的指针指向新结点,L为头指针 -
尾插法:将新结点插入到当前链表的表尾上,为此必须增加一个尾指针 rrr,使其始终指向当前链表的尾结点。
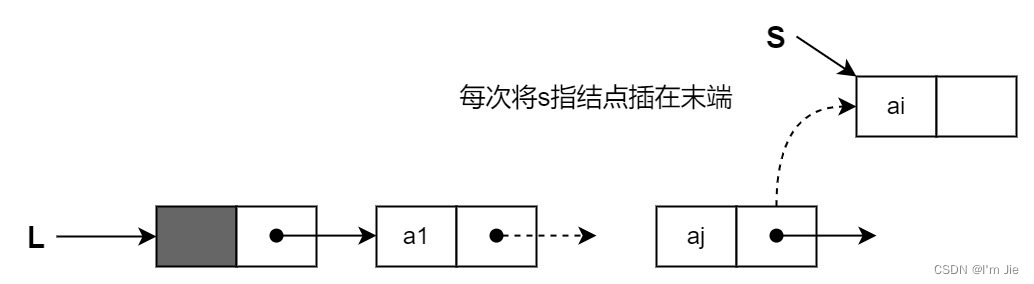
r->next=s; //原链表中的尾结点(r所指)的指针指向新结点 r=s; //r指向新的表尾结点
-
-
插入
将值为xxx的新结点插入到单链表的第iii个位置。先检查插入位置的合法性,然后找到待插入位置的前驱结点,即第i−1i-1i−1 个结点,再在其后插入新结点。
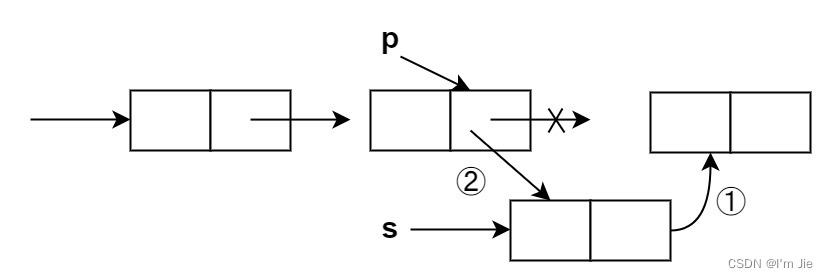
p=GetElem(L,i-1); //查找插入位置的前驱结点 s->next=p->next; //①s的指针指向p的下一结点 p->next-s; //②p的指针指向s -
删除
将单链表的第iii个结点删除。先检查删除位置的合法性,然后查找表中第i−1i-1i−1 个结点,即被删结点的前驱结点,再将其删除。
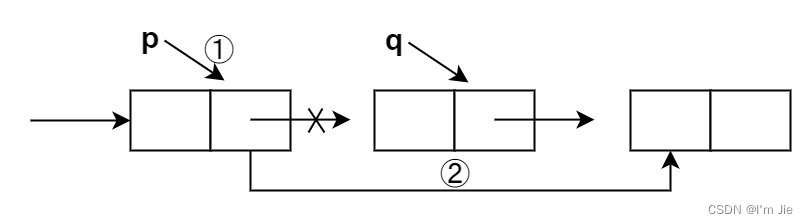
p=GetElem(L,i-1); //查找删除位置的前驱结点 q=p->next; //令q指向被删除结点 p->next=q->next; //将*q结点从链中"断开" delete q; //释放待删结点所占空间 -
求表长
- 不含头结点:从首结点开始依次顺序访问表中的每个结点,为此需要设置一个计数器变量,每访问一个结点,计数器加111,直到访问到NULLNULLNULL为止。
- 不带头结点的单链表的表长时,对空结点需要单独处理。
len=0; //1en表示单链表长度,初值设为0 LNode *p=L->next; //令p指向单链表的第一个结点 while(p) {len++;p=p->next;} //跳出循环时,len的值即为单链表的长度
第三章 栈和队列
考点 4:栈和队列的基本性质
| 术语 | 定义 |
|---|---|
| 栈 | 只允许在表的一端(栈顶)进行插入或删除的线性表。栈的操作特性为先进后出。 |
| 队列 | 只允许在表尾(队尾)插入,表头(队头)删除的线性表。队列的操作特性为先进先出。 |
nnn个不同的元素进栈,则不同出栈序列个数为1n+1C2nn\frac{1}{n+1} C_{2 n}^{n}n+11C2nn。
考点5:循环队列
定义:把顺序存储的队列从逻辑上视为一个环,称为循环队列。通常利用除模取余运算(%)(\%)(%)来实现循环。
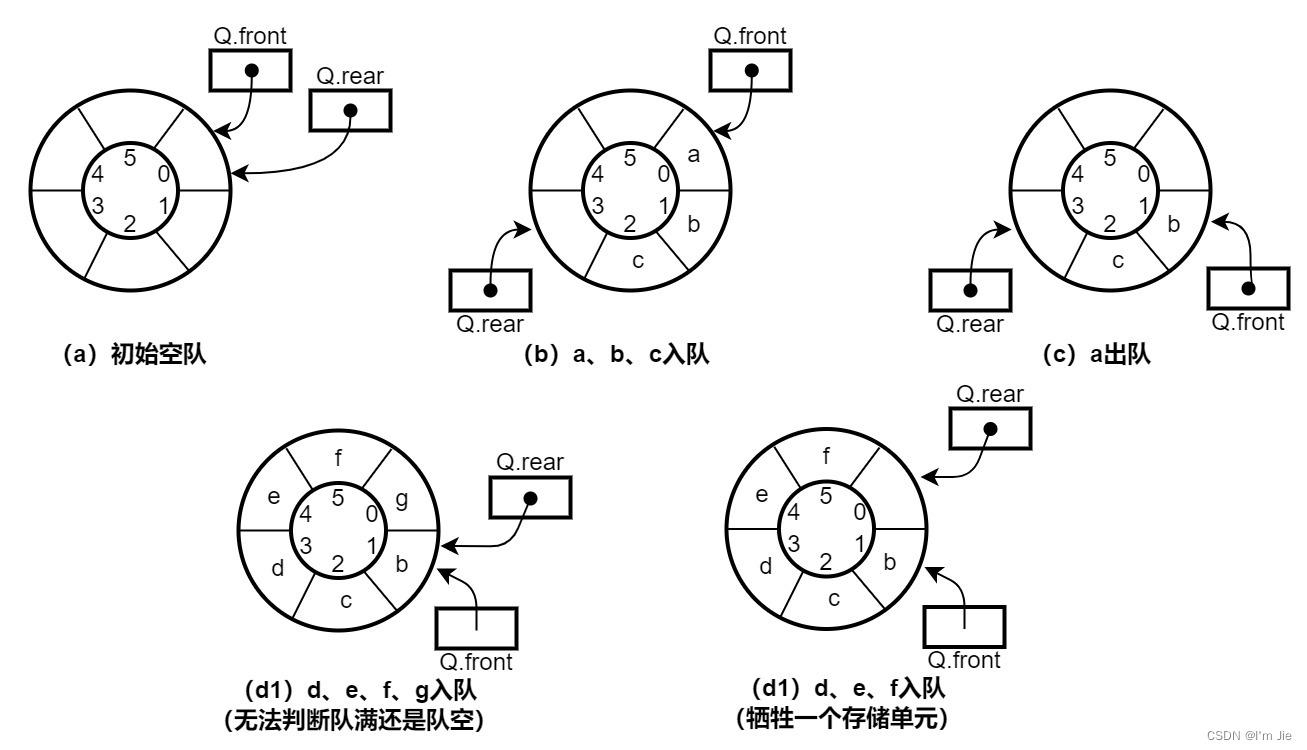
基本操作
-
元素出队:
Q.front=(Q.front+1)%MaxSize -
元素入队:
Q.rear=(Q.rear+l)%MaxSize -
队列长度:
(Q.rear-Q.front+-MaxSize)%MaxSize(frontfrontfront指向第一个元素、rearrearrear指向最后一个元素的下一位置)
为了区分是队空还是队满,通常采用牺牲一个存储单元的方法,约定以“队头指针在队尾指针的下一位置作为队满的标志”。
队满条件:
(Q.rear+1)%MaxSize==Q.front队空条件:
Q.front==Q.rear
考点6:双端队列
定义:允许两端都可以进行入队和出队操作的队列,即每个元素仅有一个前驱结点和一个后继结点(首位元素除外)。将队列的两端分别称为前端和后端。

基本操作
-
进队:前端进的元素排在后端进的元素的前面,后端进的元素排在前端进的元素的后面。
-
出队:无论是前端出队还是后端出队,先出的元素排列在后出的元素的前面。
输出受限的双端队列
定义:允许在一端进行插入和删除,但在另一端只允许插入的双端队列。

输入受限的双端队列
定义:允许在一端进行插入和删除,但在另一端只允许删除的双端队列。

考点7:栈与队列的应用
| 栈的应用 | 队列的应用 |
|---|---|
| 数制转换 | 层序遍历二叉树 |
| 括号匹配 | 缓冲区 |
| 表达式求值 | 进程的就绪队列 |
| 给定进栈和出栈顺序确定该栈的最小容量(最大深度) | 广度优先遍历BFSBFSBFS |
考点 8:特殊矩阵的存储
存储方式
- 按行优先存储
- 按列优先存储
特殊矩阵
-
对称矩阵
存储方式:只存放主对角线和下三角区的元素。
-
三角矩阵
-
下三角矩阵:上三角区的所有元素均为同一常量,存储完下三角区和主对角线上的元素之后,紧接着存储对角线上方的常量一次。

-
上三角矩阵:下三角区的所有元素均为同一常量,存储完上三角区和主对角线上的元素之后,紧接着存储对角线下方的常量一次。

-
第四章 串
考点 9:串的模式匹配算法
-
简单模式匹配算法
算法思想:从主串SSS的第一个字符起,与模式TTT的第一个字符比较,若相等,则继续逐个比较后续字符;否则从主串的下一个字符起,重新和模式的字符比较;以此类推,直至模式TTT中的每个字符依次和主串SSS 中一个连续的字符序列相等,则称匹配成功,否则称匹配不成功。简单模式匹配算法的最坏时间复杂度为O(mn)O(mn)O(mn)。
算法代码
int Index(SString S,SString T){int i=1,j=1;while(i<=S.length && j<=T.length){ if(S.ch[i]==T.ch[j]){ ++1;++j;//继续比较后继字符 }else{ i=i-j+2;j=1;//指针后退重新开始匹配 }}if(j>T.length) return i-T.length;else return 0; } -
KMPKMPKMP 算法
前缀:指除最后一个字符以外,字符串的所有头部子串。
后缀:指除第一个字符外,字符串的所有尾部字串。
部分匹配值:字符串的前缀和后缀的最长相等前后缀长度。
匹配失败时子串需要向后移动的位数:移动位数=已匹配的字符数-最后一位匹配字符对应的部分匹配值。
Next 数组计算
- 计算模式串中每个位置所对应的字串的最长前缀长度(最后一个位置所对应的字串无须计算),记为next1next1next1。
- next1next1next1右移111位,第111位补−1-1−1,得nextnextnext数组。
第五章 树与二叉树
考点 10:树的基本性质
树的基本术语
| 术语 | 定义 |
|---|---|
| 结点的度 | 树中一个结点的子结点个数 |
| 树的度 | 树中结点的最大度数 |
| 分支结点 | 度大于 0 的结点称为分支结点 |
| 叶子结点 | 度等于 0 的结点称为叶子结点 |
| 结点的深度 | 从根结点到该结点的路径上结点的个数之和(根结点深度为 1) |
| 树的高度 | 树中结点的最大层数(根结点为第一层) |
| 路径 | 树中两个结点之间所经过的结点序列 |
| 路径长度 | 路径上所经过的边的条数 |
- 树可以是空树(结点数=0)。
- 森林可以是空森林(树个数=0)。
树的基本性质
- 树中的结点总数等于总度数加 1(结点总数=边总数 +1)。
- 度为mmm的树中第hhh层最多有mh−1m^{h-1}mh−1个结点。
- 高度为hhh的mmm叉树最多有(mk−1)/(m−1)(m^k-1)/(m-1)(mk−1)/(m−1)个结点。
- 具有nnn个结点的mmm叉树的最小高度为⌈logm(n(m−1)+1)⌉\left\lceil\log_{m}{\left(n\left(m-1\right)+1\right)}\right\rceil⌈logm(n(m−1)+1)⌉。
考点 11:特殊二叉树的定义与性质
特殊二叉树
| 术语 | 定义 |
|---|---|
| 满二叉树 | 一棵高度为hhh,并且含有2h−12^h-12h−1个结点的二叉树称为满二叉树。满结点。 |
| 完全二叉树 | 一棵高度为hhh,有nnn个结点的二叉树,仅当其每个结点都与高度为hhh个结点的二叉树,仅当其每个结点都与高度为hhh的满二叉树中编号为1∼n1\sim n1∼n 的结点一一对应,称为完全二叉树。 |
完全二叉树的性质
- 最后一个分支结点(非叶结点)的编号:⌊n/2⌋\left \lfloor n/2 \right \rfloor⌊n/2⌋。
- 叶子结点只可能在层次最大的两层上出现。
- 如果有度为111 的结点,只可能有一个,且该结点只有左孩子。
- 若nnn为奇数,则每个分支结点都有左子女和右子女;若nnn 为偶数,则编号最大的分支结点只有左子女。
- 结点iii所在层次(深度)为⌊log2i⌋+1\left\lfloor\log _{2} i\right\rfloor+1⌊log2i⌋+1。
- 具有nnn个(n>0)(n>0)(n>0)结点的完全二叉树的高度为⌊log2(n+1)⌋\left\lfloor\log _{2} (n+1)\right\rfloor⌊log2(n+1)⌋或⌊log2n⌋+1\left\lfloor\log _{2} n\right\rfloor+1⌊log2n⌋+1。
- 编号为iii的结点的双亲结点的编号为⌊i/2⌋\left \lfloor i/2 \right \rfloor⌊i/2⌋;左孩子编号为2i2i2i;右孩子编号为2i+12i+12i+1。
考点 12:二叉树的遍历
遍历方式
- 先序遍历:先访问根结点,再访问左子树,最后访问右子树。
- 中序遍历:先访问左子树,再访问根结点,最后访问右子树。
- 后序遍历:先访问左子树,再访问右子树,最后访问根结点。
- 层序遍历:按自顶向下、自左向右的顺序来逐层访问树中结点。
构造二叉树
- 中序序列与前序序列。
- 中序序列与后序序列。
- 中序序列与层序序列。
唯一确定一棵二叉树的序列组合(都需要中序序列)
考点 13:树、森林与二叉树的转换
规则:左结点指向孩子结点,右结点指向兄弟结点(左孩子右兄弟)。
考点 14:线索二叉树
结点结构

线索:利用空链域存放指向直接前驱或直接后继的指针。
线索化:对二叉树遍历使其变为线索二叉树。线索化时,若无左子树,则令IchildIchildIchild指向其前驱结点;若无右子树,则令rchildrchildrchild指向其后继结点。两个tagtagtag标志域表明当前指针域所指对象是指向左(右)子结点还是直接前驱(后继)。
ltag ={0,lchild域指示结点的左孩子 1,lchild域指示结点的前驱 rtag={0,rchild域指示结点的右孩子 1,rchild域指示结点的后继 \text { ltag }=\left\{\begin{array}{ll} 0, & \text { lchild域指示结点的左孩子 } \\ 1, & \text { lchild域指示结点的前驱 } \end{array}\right.\operatorname{rtag}=\left\{\begin{array}{ll} 0, & \text { rchild域指示结点的右孩子 } \\ 1, & \text { rchild域指示结点的后继 } \end{array}\right. ltag ={0,1, lchild域指示结点的左孩子 lchild域指示结点的前驱 rtag={0,1, rchild域指示结点的右孩子 rchild域指示结点的后继
在有 N 个结点的二叉树中,有 N+1 个空指针域。
考点 15:哈夫曼
哈夫曼树
树的带权路径长度:树中所有叶结点的带权路径长度之和。wiw_iwi是第iii个叶结点所带的权值;lil_ili是该叶结点到根结点的路径长度。
WPL=∑i=1nwili\mathrm{WPL}=\sum_{i=1}^{n} w_{i} l_{i} WPL=i=1∑nwili
哈夫曼树:带权路径长度最小的二叉树。
构造哈夫曼树
- 构造一个新结点,选取两个权值最小的结点作为新结点的左、右子树,新结点的权值置为左、右子树上根结点的权值之和。
- 从序列中删除刚才选出的两个结点,同时将新结点加入序列。
哈夫曼树特点
- 每个初始结点最终都成为叶结点,并且权值越小的结点到根结点的路径长度越大。
- 哈夫曼树中结点总数为2N−12N-12N−1。
- 哈夫曼树中不存在度为111的结点。
- 同一序列构造的哈夫曼树不唯一,但带权路径长度唯一且最优。
哈夫曼编码
前缀编码:没有一个编码是另一个编码的前缀。
哈夫曼编码构造
-
根据待编码元素构造对应的哈夫曼树。
-
从根至该字符的路径上进行标记,“左孩子”的边标记为000,“右孩子”的边标记为111。
-
从根结点到待编码元素结点的路径形成的000、111序列就是哈夫曼编码。
第六章 图
考点 16:图的基本概念
基本术语
-
无向图 有向图 边:顶点的无序对,记为(v,w)(v,w)(v,w)或(w,v)(w,v)(w,v) 弧:顶点的有序对,记为<v,w><v,w><v,w>,vvv称为弧尾,www 称为弧头 无向图:若EEE是无向边(简称边)的有限集合时,则图GGG为无向图 有向图:若EEE是有向边(也称弧)的有限集合时,则图GGG为有向图 顶点的度:指依附于该顶点的边的数量,记为TD(v)TD(v)TD(v) 顶点的度:入度和出度之和(入度是以vvv为终点的有向边的数目;出度是以vvv为起点的有向边的数目) 连通:从顶点vvv到顶点www有路径存在,则称vvv和www 是连通的 强连通:从顶点vvv到顶点www和从顶点www到顶点vvv之间都有路径,则称vvv和www 是强连通的 连通图:图中任意两个顶点都是连通的,则称图GGG为连通图,否则为非连通图 强连通图:图中任意一对项点都是强连通的,则称此图为强连通图 连通分量:图的极大连通子图称为连通分量 强连通分量:图的极大强连通子图称为有向图的强连通分量 无向完全图:任意两个顶点之间都存在边,共有(n−1)/2(n-1)/2(n−1)/2条边 有向完全图:任意两个顶点之间都存在方向相反的两条弧,共有n(n−1)n(n-1)n(n−1)条有向边
| 术语 | 定义 |
|---|---|
| 生成树 | 连通图的生成树是包含图中全部顶点的一个极小连通子图 |
| 生成森林 | 非连通图的连通分量的生成树构成了非连通图的生成森林 |
| 回路(环) | 第一个顶点和最后一个顶点相同的路径称为回路或环 |
- 极大连通子图:包含了图中尽可能多的顶点以及尽可能多的边
- 极小连通子图:包含图中全部顶点且包含边最少
图的基本性质
- 无向图中任意顶点的入度等于出度。
- 无向图中(无论是否连通),所有顶点的度数之和等于边数的两倍。
- 在有向图中,全部顶点的“入度之和”=“出度之和”=边数。
- 图的邻接矩阵表示中,各顶点的度等于矩阵中该结点对应的行(对应出度)和列(对应入度)的非零元素数量之和。
考点 17:图的存储及基本操作
邻接矩阵存储法
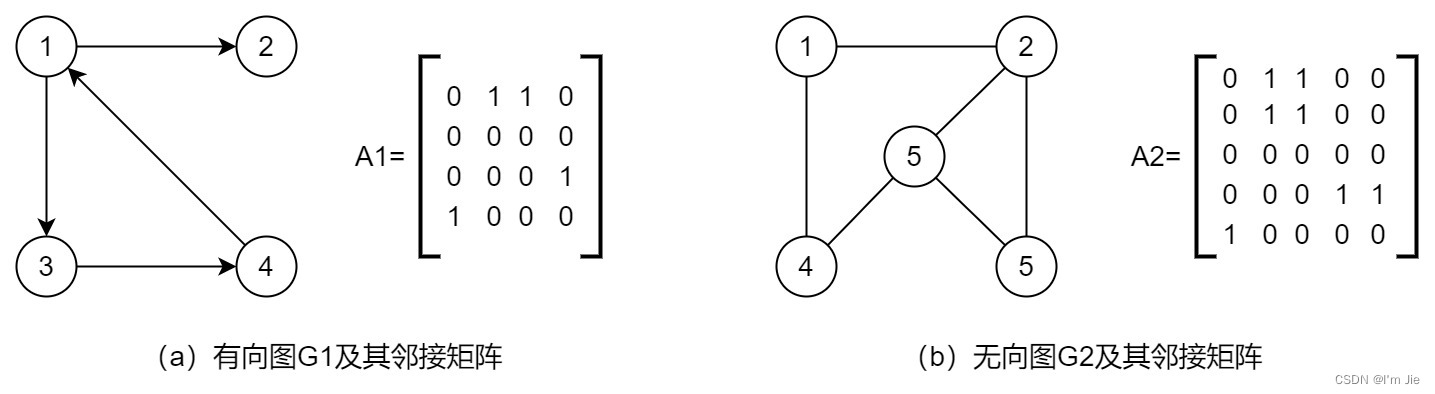
方式:用一个一维数组存储图中顶点的信息,用一个二维数组存储图中边的信息
特点
-
无向图的邻接矩阵一定是一个对称矩阵,可采用压缩存储。有向图的邻接矩阵不一定是对称矩阵,有向完全图的邻接矩阵是对称矩阵。
-
对于无向图,邻接矩阵的第iii行(或第iii列)非零元素(或非∞∞∞元素)的个数正好是第
iii个顶点的度。
-
对于有向图,邻接矩阵的第iii行(或第iii列)非零元素(或非∞∞∞元素)的个数正好是第iii个顶点的出度(或入度)。
-
对于无权图的邻接矩阵AAA(矩阵中各位置的值为000或111),An[i][j]\left.A^{n}[i][j\right]An[i][j]的值表示由顶点iii到顶点jjj的路径长度为nnn的路径的数量。
-
稠密图适合使用邻接矩阵的存储表示。
邻接表存储法
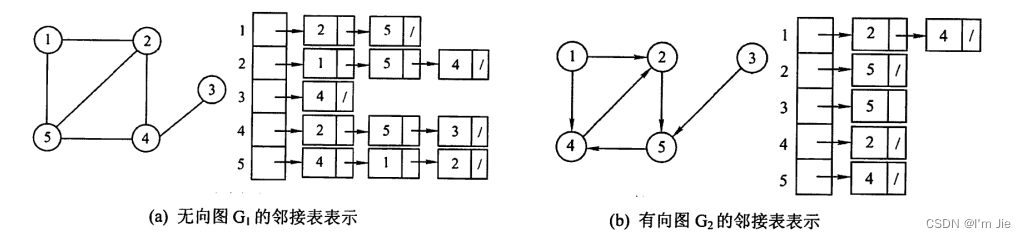
方式
- 将图中所有邻接于顶点vvv的顶点链成一个单链表,这个单链表就称为顶点vvv 的邻接表。
- 将所有顶点的邻接表的表头放到数组中,就构成了图的邻接表。
特点:
-
若无向图有nnn个顶点、eee条边,则其邻接表仅需nnn个头结点和2e2e2e个表结点。
-
对于无向图,顶点viv_ivi的度等于第iii个链表中的结点数;对于有向图,第iii 个链表中的结点数只是顶点viv_ivi的出度,求入度,必须遍历整个邻接表。
-
在邻接表上容易找到任一顶点连接的所有边。但要判定任意两个顶点(viv_ivi和vjv_jvj)之间是否有边或弧相连,则需搜索第iii个或第jjj 个链表,在这方面不及邻接矩阵方便。
-
图的邻接表不唯一,取决于建立邻接表的算法以及边的输入次序。
考点 18:图的遍历
广度优先搜索 BFS
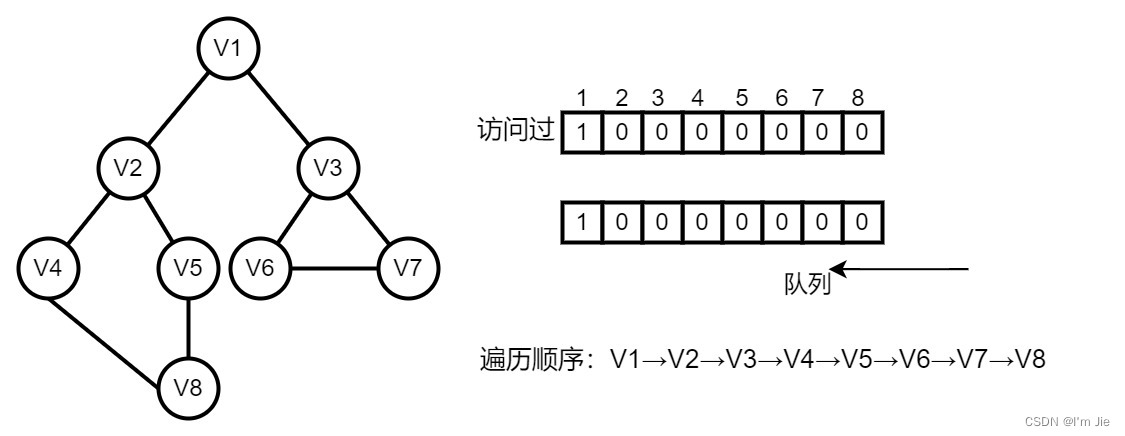
遍历过程
- 访问起始顶点vvv。
- 依次访问顶点vvv未访问过的邻接顶点v2v_2v2,v3v_3v3。直到图中所有和vvv连通的顶点都被访问过为止。
- 另选一个未被访问过的顶点作为起始顶点 vvv,重新开始,直至所有顶点都被访问。
性能分析
- BFSBFSBFS算法需要借助一个辅助队列,空间复杂度为O(∣V∣)O(|V|)O(∣V∣)。
- 邻接矩阵表示时,算法总的时间复杂度为O(∣V∣2)O(|V|^2)O(∣V∣2)。
- 邻接表表示时,算法总的时间复杂度为O(∣V∣+∣E∣)O(|V|+|E|)O(∣V∣+∣E∣)。
深度优先搜索 DFS
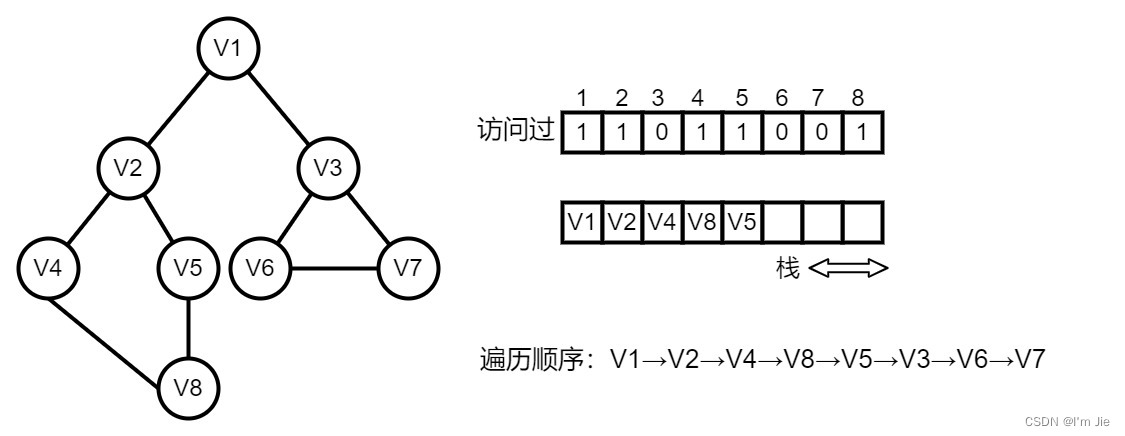
遍历过程
- 访问起始顶点vvv。
- 访问与顶点vvv邻接且未被访问过的任一邻接顶点v2v_2v2。再访问与v2v_2v2邻接且未被访问的任一顶点v3v_3v3。
- 当不能再继续向下访问时,依次退回到最近被访问的顶点,若它还有邻接顶点未被访问,则从该顶点重新开始,直到图中所有顶点均被访问过为止。
性能分析
- DFSDFSDFS算法需要借助一个递归工作栈,空间复杂度为O(∣V∣)O(|V|)O(∣V∣)。
- 邻接矩阵表示时,算法总的时间复杂度为O(∣V∣2)O(|V|^2)O(∣V∣2)。
- 邻接表表示时,算法总的时间复杂度为O(∣V∣+∣E∣)O(|V|+|E|)O(∣V∣+∣E∣)。
对于同一个图,基于邻接矩阵的遍历所得到的DFSDFSDFS序列和BFSBFSBFS序列是唯一的;由于邻接表不唯一,所以基于邻接表的遍历所得到的DFSDFSDFS序列和BFSBFSBFS序列可能不唯一。
考点 19:最小(代价)生成树
定义:所有生成树的集合中边的权值之和最小的那棵生成树。
性质
- 最小生成树不唯一。
- 当图中的各边权值互不相等时,G 的最小生成树唯一。
- 最小生成树所对应的边的权值之和总是唯一的,而且是最小的。
- 最小生成树是一棵无向连通带权图。
Prim 算法
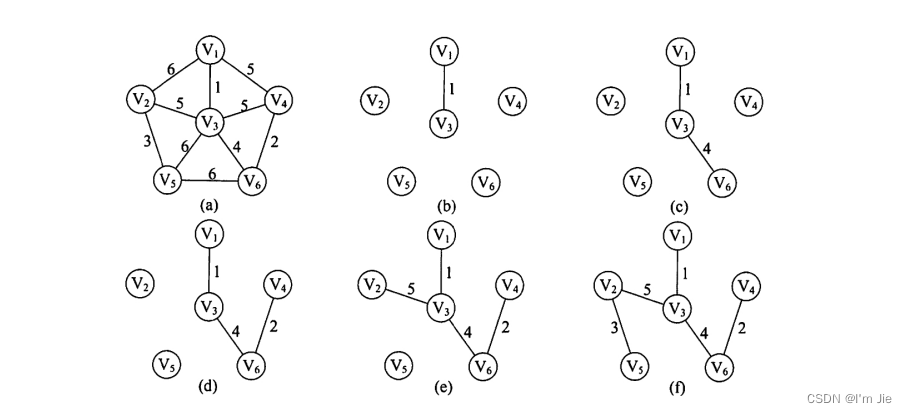
-
每次在已选顶点的邻接边中选权值最小的边加入。
-
PrimPrimPrim算法的时间复杂度为O(∣V∣2)O(|V|^2)O(∣V∣2),不依赖于EEE,适用于边稠密的图。
Kruskal 算法
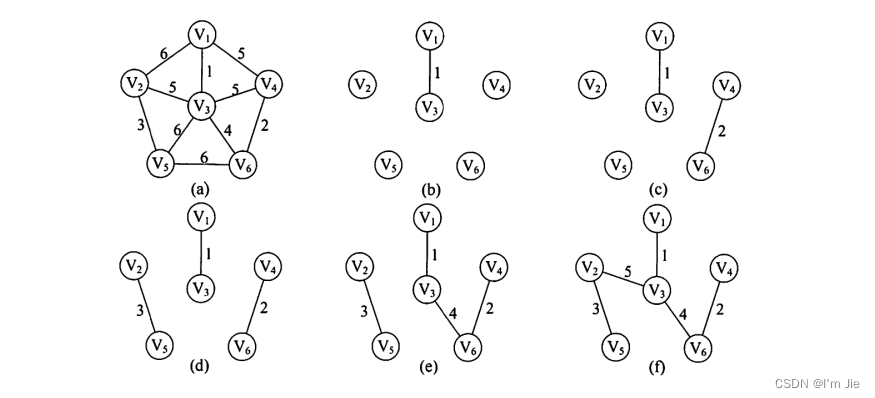
-
不断选取当前未被选取的权值最小的边,若其两个顶点不属于同一顶点集合,则将该边放入生成树的边集,同时将两个顶点所在的集合合并。
-
直到选取了n−1n-1n−1条边为止。
-
KruskalKruskalKruskal算法的时间复杂度为O(∣E∣log2∣E∣)O\left(|E| \log _{2}|E|\right)O(∣E∣log2∣E∣),适用于边稀疏而顶点较多的图。
考点 20:最短路径
最短路径(权值)问题
- 单源最短路径问题:求从给定源点到其他各个顶点的最短路径长度。
- 点对点最短路径问题:求每一对顶点之间的最短路径长度。
Dijkstra 算法
用邻接矩阵arcsarcsarcs表示带权有向图 arcs[i][j]={eij,eij为有向边 <i,j>的权值 ∞,不存在有向边 <i,j>\operatorname{arcs}[i][j]=\left\{\begin{array}{ll} e_{i j}, & e_{i j} \text { 为有向边 }<i, j>\text { 的权值 } \\ \infty, & \text { 不存在有向边 }<i, j> \end{array}\right.arcs[i][j]={eij,∞,eij 为有向边 <i,j> 的权值 不存在有向边 <i,j>
算法过程
-
dist[]dist[]dist[]:记录了从源点v0v_0v0到其他各顶点当前的最短路径长度。
-
集合 SSS 记录已求得的最短路径的顶点,每趟确定一个最短路径。
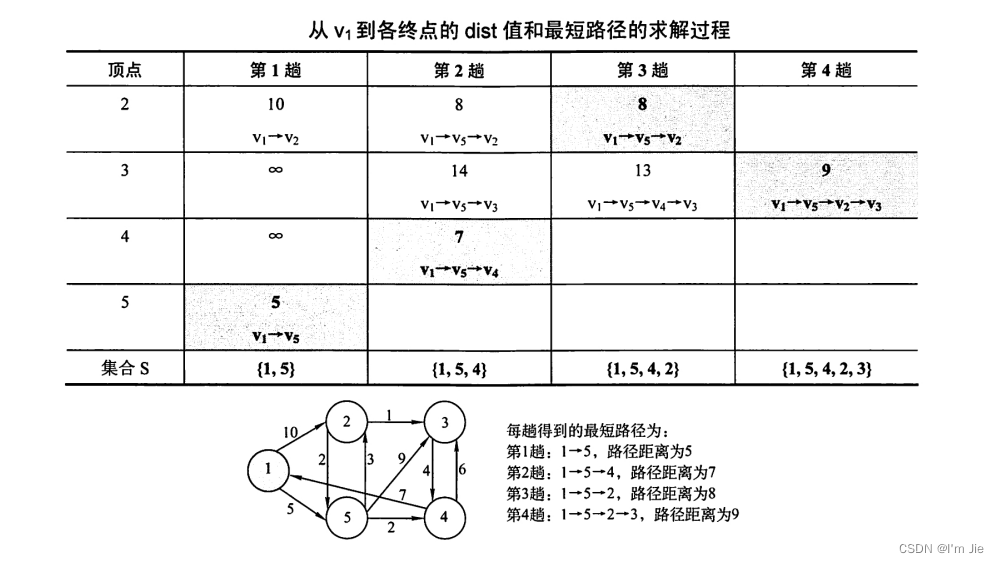
Floyd 算法
算法过程
-
定义一个 n 阶方阵序列:A(−1),A(0),⋯,A(n−1)。A^{(-1)}, A^{(0)}, \cdots, A^{(n-1)}。A(−1),A(0),⋯,A(n−1)。
-
A(−1)[i][j]=arcs[i][j]A^{(-1)}[i][j]=\operatorname{arcs}[i][j]A(−1)[i][j]=arcs[i][j](((arcs[i][j]\operatorname{arcs}[i][j]arcs[i][j]与迪杰斯特拉算法中的定义相同)))。
-
递推产生A(k)[i][j]=Min{A(k−1)[i][j],A(k−1)[i][k]+A(k−1)[k][j]},k=0,1,⋯,n−1A^{(k)}[i][j]=\operatorname{Min}\left\{A^{(k-1)}[i][j], \quad A^{(k-1)}[i][k]+A^{(k-1)}[k][j]\right\}, \quad k=0,1, \cdots, n-1A(k)[i][j]=Min{A(k−1)[i][j],A(k−1)[i][k]+A(k−1)[k][j]},k=0,1,⋯,n−1。
-
A(k)[i][j]A(k)[i][j]A(k)[i][j]是从顶点viv_ivi到到到vjv_jvj、中间顶点的序号不大于kkk的最短路径的长度。
-
经过nnn次迭代后所得到的A(n−1)[i][j]A(n-1)[i][j]A(n−1)[i][j]就是viv_ivi到vjv_jvj 的最短路径长度。
Floyd 算法的时间复杂度为O(∣V∣3)O(|V|^3)O(∣V∣3)。
Floyd 算法允许图中有带负权值的边,但不允许有包含带负权值的边组成的回路。
考点 21:拓扑排序
定义
- 有向无环图的顶点组成的序列。
- 每个顶点出现且只出现一次。
- 每个有向无环图都有一个或多个拓扑序列。
算法过程
- 从有向无环图中选择一个没有前驱的顶点并输出。
- 从图中删除该顶点和所有以它为起点的有向边。
- 直到当前的图为空或当前图中不存在无前驱的项点为止(环)。
拓扑排序的时间复杂度为O(∣V∣+∣E∣)O(|V|+|E|)O(∣V∣+∣E∣)。
考点 22:关键路径
AOE 网:带权有向图以顶点表示事件,有向边表示活动,边上的权值表示完成该活动的开销。
关键路径:AOE 网中从源点到汇点的最大路径长度的路径,关键路径长度是整个工程所需的最短工期。
关键活动:关键路径上的活动。
性质
- 可以通过加快关键活动缩短整个工程的工期。并非关键活动缩短多少工期就缩短多少,因为缩短到一定的程度,该关键活动可能变成非关键活动了。
- 关键路径并不唯一。对于有几条关键路径的网,只提高一条关键路径上的关键活动速度并不能缩短整个工程的工期,只有加快那些包括在所有关键路径上的关键活动才能达到缩短工期的目的。
- 从源点到汇点的路径上,所有具有最大路径长度的路径,都是关键路径。所有“最长路径”(关键路径)上的所有活动,都是关键活动。
求关键路径算法
参数定义
- 事件vkv_kvk的最早发生时间ve(k)ve(k)ve(k):从源点到顶点VkV_kVk的最长路径长度
ve(k)={0,k=0,vk是源点max{ve(j)+Weight(vj,vk)},Weight(vj,vk)表示<vj,vk>上的权值\operatorname{ve}(k)=\left\{\begin{array}{ll}0, & k=0, \mathrm{v}_{k} \text { 是源点} \\\max \left\{\operatorname{ve}(j)+\text {Weight}\left(\mathrm{v}_{j},\mathrm{v}_{k}\right)\right\}, & \text{Weight}\left(\mathrm{v}_{j}, \mathrm{v}_{k}\right) \text {表示}\left.<\mathrm{v}_{j},\mathrm{v}_{k}>\right.\text {上的权值}\end{array}\right. ve(k)={0,max{ve(j)+Weight(vj,vk)},k=0,vk 是源点Weight(vj,vk)表示<vj,vk>上的权值
- 事件vkv_kvk的最迟发生时间vl(k)vl(k)vl(k):从顶点VkV_kVk到汇点的最短路径长度
vl(j)={ve(n−1),j=n−1,vj是汇点 min{vl(k)−Weight(vj,vk)},Weight(vj,vk)表示<vj,vk>的权值\operatorname{vl}(j)=\left\{\begin{array}{ll} \mathrm{ve}(n-1), & j=n-1, \mathrm{v}_{j} \text { 是汇点 } \\ \min \left\{\mathrm{vl}(k)-\operatorname{Weight}\left(\mathrm{v}_{j}, \mathrm{v}_{k}\right)\right\}, & \text { Weight}\left(\mathrm{v}_{j}, \mathrm{v}_{k}\right) \text {表示}<\mathrm{v}_{j}, \mathrm{v}_{k}>\text {的权值} \end{array}\right. vl(j)={ve(n−1),min{vl(k)−Weight(vj,vk)},j=n−1,vj 是汇点 Weight(vj,vk)表示<vj,vk>的权值
- 活动aia_iai的最早开始时间e(i)e(i)e(i):该活动的起点所表示的事件最早发生时间
e(i)=ve(k)e(i)=ve(k) e(i)=ve(k)
- 活动aia_iai的最迟开始时间l(i)l(i)l(i):该活动的终点所表示的事件最迟发生时间与该活动所需时间之差
l(i)=vl(j)−Weight(vk,vj)\mathrm{l}(i)=\operatorname{vl}(j)-\operatorname{Weight}\left(\mathrm{v}_{k}, \mathrm{v}_{j}\right) l(i)=vl(j)−Weight(vk,vj)
算法过程
-
求AOEAOEAOE网中所有事件的最早发生时间ve()ve()ve()
从源点出发,到该顶点的最大长度。
-
求 AOE 网中所有事件的最迟发生时间vl()vl()vl()
事件的最迟发生时间=关键路径长度-从该顶点到汇点的最大长度。
-
求 AOE 网中所有活动的最早开始时间e()e()e()
活动的最早开始时间=该活动的起点所代表的事件的最早发生时间。也就是从源点出发,到这条边的起始点的最大长度。
-
求 AOE 网中所有活动的最迟开始时间l()l()l()
活动的最迟开始时间=关键路径长度-(从这条边的终点到汇点的最大长度 + 这条边的长度)。
-
求 AOE 网中所有活动的差额d()=l()−e()d()=l()-e()d()=l()−e(),找出所有d()=0d()=0d()=0(最早开始时间=最迟开始时间)的活动构成关键路径。若活动的最迟开始时间 > 最早开始时间,则该活动不是关键活动。
第七章 查找
考点 23:查找的基本术语
查找:在数据集合中寻找满足某种条件的数据元素的过程称为查找。查找的结果一般分为查找成功、查找失败。
查找表(查找结构):用于查找的数据集合称为查找表,它由同一类型的数据元素(或记录)组成,可以是一个数组或链表等数据类型。对查找表经常进行的操作一般有444 种:
- 查询某个特定的数据元素是否在查找表中
- 检索满足条件的某个特定的数据元素的各种属性
- 在查找表中插入一个数据元素
- 从查找表中删除某个数据元素
静态查找表:若一个查找表的操作只涉及上述操作 ① 和 ②,则无须动态地修改查找表,此类查找表称为静态查找表;需要动态地插入或删除的查找表称为动态查找表。适合静态查找表的查找方法有顺序查找、折半查找、散列查找等;适合动态查找表的查找方法有二叉排序树的查找、散列查找等。二叉平衡树和 B 树都是二叉排序树的改进。
关键字:数据元素中唯一标识该元素的某个数据项的值,使用基于关键字的查找,查找结果应该是唯一的。
平均查找长度:在查找过程中,一次查找的长度是指需要比较的关键字次数,而平均查找长度则是所有查找过程中进行关键字的比较次数的平均值,其数学定义为
ASL=∑i=1nPiCi\mathrm{ASL}=\sum_{i=1}^{n} P_{i} C_{i} ASL=i=1∑nPiCi
式中,nnn是查找表的长度;PiP_iPi是查找第iii个数据元素的概率,一般认为每个数据元素的查找概率相等,Pi=1/nP_i=1/nPi=1/n;CiC_iCi是找到第iii 个数据元素所需进行的比较次数。平均查找长度是衡量查找算法效率的最主要的指标。
考点 24:顺序查找
算法:逐个比较查找表中的元素,直到找到目标元素或达到查找表的尽头为止,时间复杂度为O(n)O(n)O(n)。
-
一般线性表
- 效率分析
查找成功时,在等概率的情况下,平均查找长度为ASL成功 =∑i=1nPi(n−i+1)=n+12\mathrm{ASL}_{\text {成功 }}=\sum_{i=1}^{n} P_{i}(n-i+1)=\frac{n+1}{2}ASL成功 =∑i=1nPi(n−i+1)=2n+1。
查找不成功时,平均查找长度为ASL不成功 =n+1\mathrm{ASL}_{\text {不成功 }}=n+1ASL不成功 =n+1。
-
算法代码
typedef struct( //查找表的数据结构ElemType *elem; //元素存储空间基址,建表时按实际长度分配,0号单元留空int TableLen; //表的长度}SSTable;int search seq(SSTab1e ST,ElemType key){ST.elem[0]=key;for(i=ST.Tab1eLen;ST.elem[i]!=key;--i);return i; //若表中不存在关键字为key的元素,将查找到i==0时退出for循环}
在算法中,将下标为000的元素当作“哨兵”。引入它的目的是使得Search_SeqSearch\_SeqSearch_Seq内的循环,不必判断数组是否会越界,因为满足i==0i==0i==0 时,循环一定会跳出。
-
有序线性表
-
算法:表内关键字有序的,则查找失败时可以不用再比较到表的另一端就返回查找失败的信息。
-
查找判定树
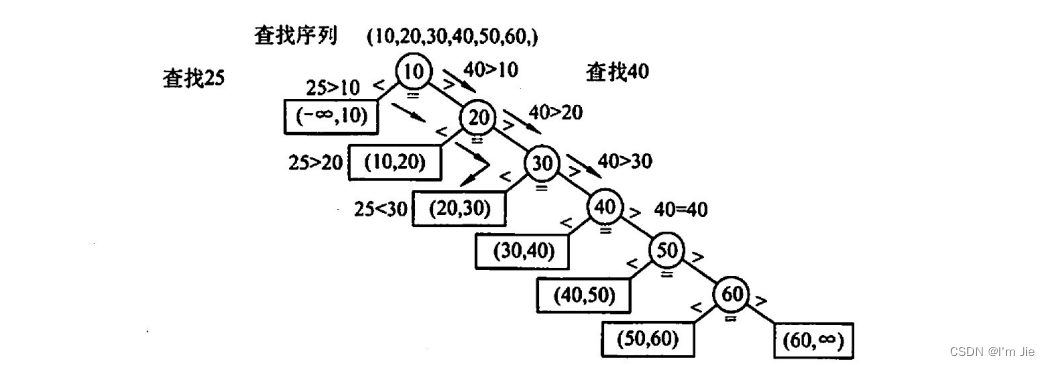
圆形结点表示有序线性表中存在的元素。
矩形结点称为失败结点(若有 n 个结点,则相应地有 n+1 个查找失败结点),描述的是那些不在表中的数据值的集合。
-
效率分析
查找成功时,在等概率的情况下,平均查找长度为ASL成功 =∑i=1nPi(n−i+1)=n+12\mathrm{ASL}_{\text {成功 }}=\sum_{i=1}^{n} P_{i}(n-i+1)=\frac{n+1}{2}ASL成功 =∑i=1nPi(n−i+1)=2n+1。
查找不成功时,平均查找长度为ASL不成功 =1+2+⋯+n+nn+1=n2+nn+1\mathrm{ASL}_{\text {不成功 }}=\frac{1+2+\cdots+n+n}{n+1}=\frac{n}{2}+\frac{n}{n+1}ASL不成功 =n+11+2+⋯+n+n=2n+n+1n。
-
相关文章:

408数据结构考点总结
文章目录第一章 绪论考点 1:时间复杂度与空间复杂度时间复杂度空间复杂度第二章 线性表考点 2:顺序表考点 3:单链表第三章 栈和队列考点 4:栈和队列的基本性质考点5:循环队列考点6:双端队列输出受限的双端队…...

虹科分享 | 网络流量监控 | 你的数据能告诉你什么:解读网络可见性的4种数据类型
要了解网络性能问题的原因,可见性是关键。而这四种数据类型(流、数据包、SNMP和API)都在增强网络可见性方面发挥着重要作用。 流 流是通过网络发送的数据的摘要。流类型不同,可以包括NetFlow, sFlow, jFlow和IPFIX。不同的流类型…...

SpringBoot日志框架使用详解
几种常见的日志级别由低到高分为:TRACE < DEBUG < INFO < WARN < ERROR < FATAL 。如何理解这个日志级别呢?很简单,如果项目中的日志级别设置为INFO ,那么比它更低级别的日志信息 就看不到了,即是TRACE…...
剑指offer-消失的数字、数组中出现的次数
消失的数字 解法一:求和相减 假设nums为[0,1,2,4],消失的数字为3,完整的数组应该是[0,1,2,3,4],则sum101247,sum20123410,我们很容易发现 sum2-sum1 01234 - 0124 3,即为消失的数字。因此,我们可以采用先…...

axios请求配置baseURL选项
在src同级目录创建 (1).env.delelopment : 开发模式时调用 (2).env.production :生产模式时调用 (3).env.testing : 测试模式时调用 # 页面标题 VITE_APP_TITLE 若依管理系统# 生产环境配…...
风储VSG-基于虚拟同步发电机的风储并网系统MATLAB仿真
MATLAB2021b版本仿真模型:风力发电机模块、储能控制模块、功率计算模块、VSG控制模块、电压电流双环控制模块。永磁同步风机输出功率、储能系统输出功率以及逆变器输出功率曲线。直流母线电压波动曲线。逆变器输出电压、电流曲线。完整模型见博主资源!&a…...
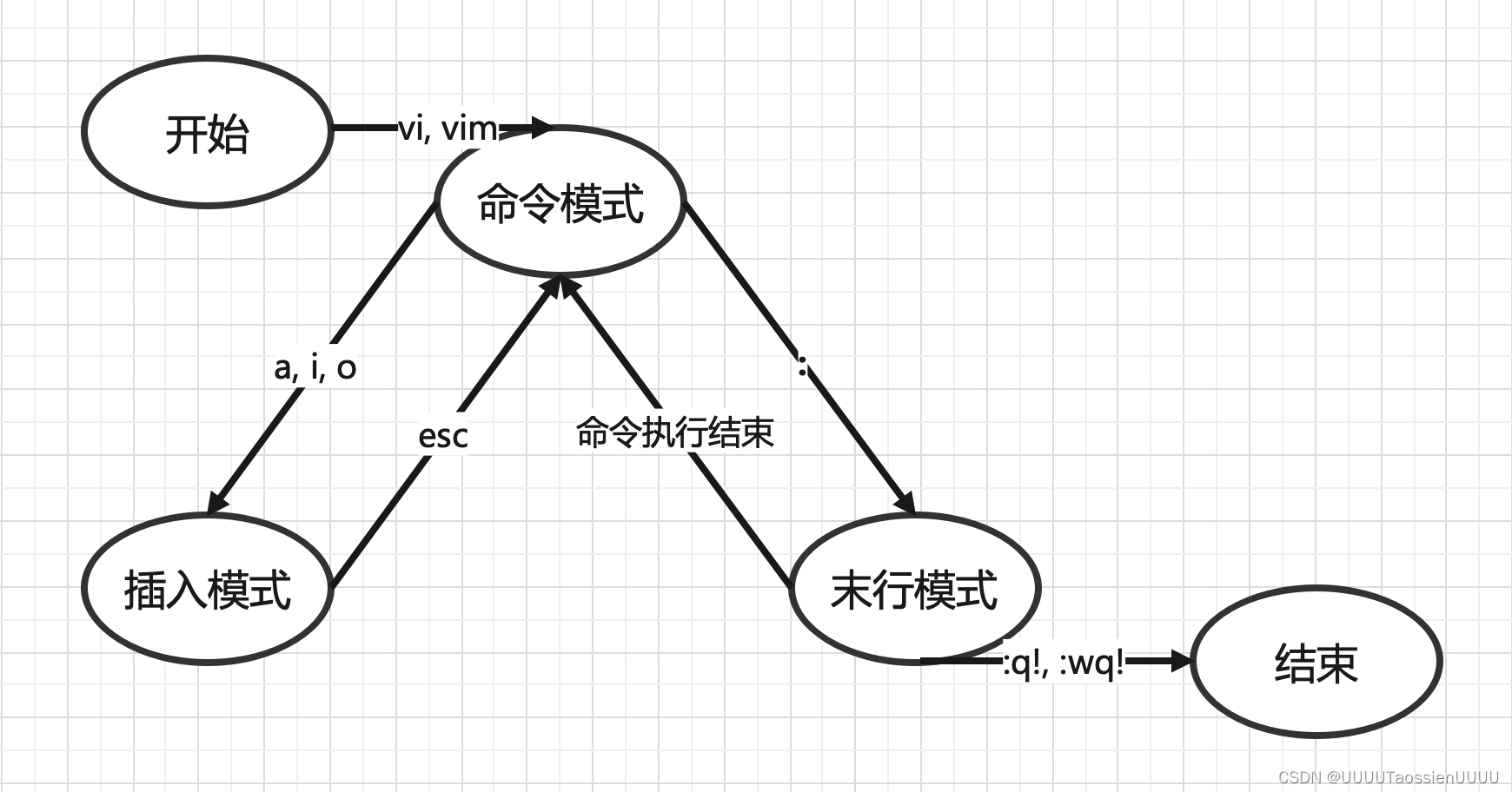
vim常用命令
vim常用三种模式 命令模式(Command mode) 插入模式(Insert mode) 末行模式(Last line mode) (一)进入命令模式 vi 或者 vim(二)命令模式 -> 插入模式 &…...

华为OD机试 - 最差产品奖 | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 简易压缩算法(Python) | 机试题算法思路 【2023】 华为OD机试题 - 获取最大软件版本号(JavaScript) 华为OD机试 - 猜字谜(Python) | 机试题+算法思路 【2023】 华为OD机试 - 删除指定目录(Python) | 机试题算法思路 【2023】 华为OD机试 …...

HR:你会Python数据分析吗?
之前看到一个段子: 以前去面试,HR会问你“精通office吗?” 现在去面试,HR会问你“会Python数据分析吗?” 图片来源:网络 大数据时代,无论是数据分析师、研发,到运营、市场、产品经…...

算法18:LeetCode_链表相关算法题
链表无小事,只要是涉及到链表的算法题,边界值的设定尤为重要,而且及其容易出错误。这就要求我们平时多加练习。但是,我们在面试和笔试的过程中往往会碰到链表相关的题目,所以我们在笔试的时候一般都会借助系统提供的工…...
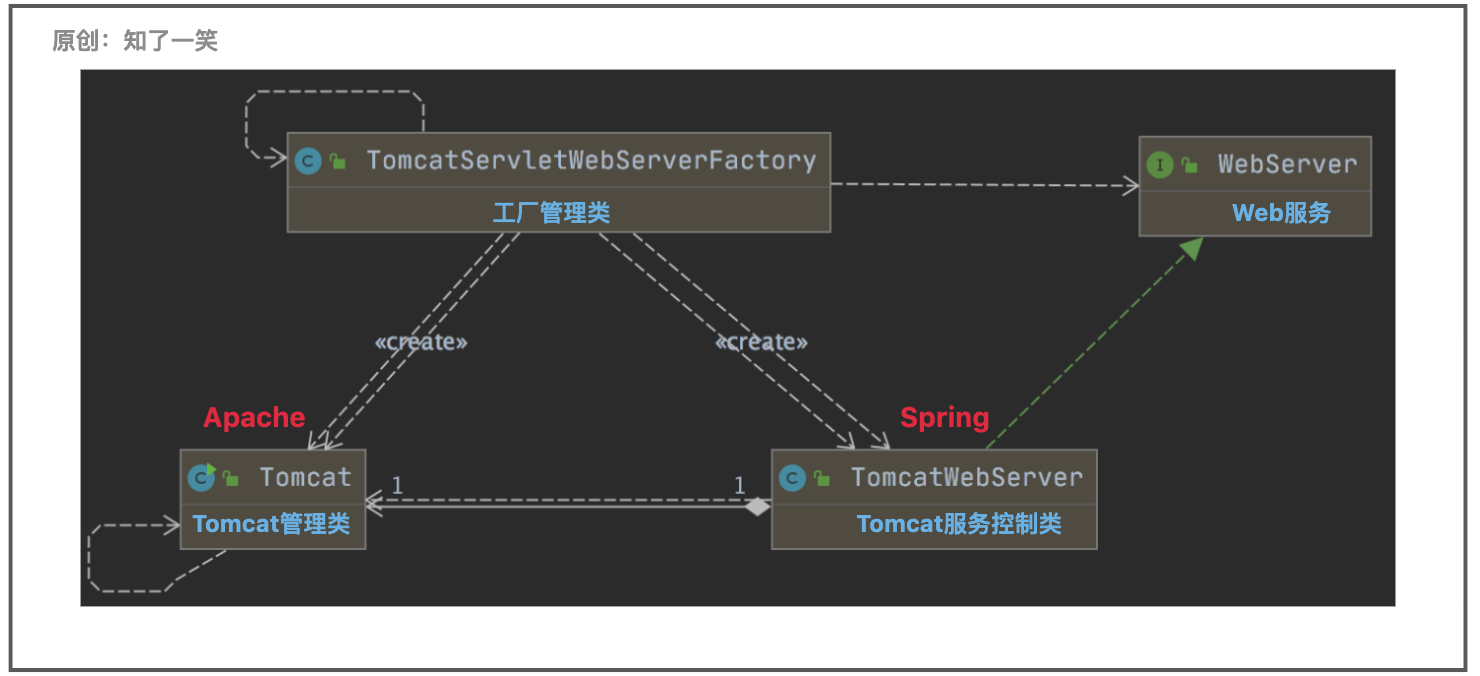
SpringBoot集成Tomcat服务
文章目录一、Tomcat集成1、依赖层级2、自动化配置二、Tomcat架构三、Tomcat配置1、基础配置2、属性配置类3、配置加载分析四、周期管理方法1、控制类2、核心方法使用的成本越低,内部封装越复杂; 一、Tomcat集成 1、依赖层级 在SpringBoot框架的web依赖…...

【机器学习】决策树-C4.5算法
1.C4.5算法 C4.5算法与ID3相似,在ID3的基础上进行了改进,采用信息增益比来选择属性。ID3选择属性用的是子树的信息增益,ID3使用的是熵(entropy, 熵是一种不纯度度量准则),也就是熵的变化值&…...
actipro-winforms-controls-23.1.0 Crack
actipro-winforms一组用于构建漂亮的 Windows 窗体桌面应用程序的 UI 控件,用于构建 IDE 的高级停靠窗口、MDI、属性网格、树控件和文件夹/文件浏览器,用于常见数据类型、自动完成、屏蔽编辑和代码编辑的强大编辑器,功能区、图表、微型图表、…...

适合打游戏用的蓝牙耳机有哪些?吃鸡无延迟的蓝牙耳机推荐
现在手游的兴起,让游戏市场变得更加火爆,各种可以提高玩家体验的外设也越来越多,除了提升操作的外置按键与手柄外,能带来更出色音质与舒心使用的游戏耳机,整体氛围感更好,让玩家在细节上占据优势࿰…...

1000:入门测试题目[不一样的题解][85种写法]【A+B问题】
题目: 1000:入门测试题目 时间限制: 1000 ms 内存限制: 32768 KB 提交数: 262857 通过数: 158152 【题目描述】 求两个整数的和。 【输入】 一行,两个用空格隔开的整数。 【输出】 两个整数的和。 【输入样例】 2 3 【输出样例】…...
FastReport .NET 2023.1.13 Crack
FastReport .NET 使用来自 ADO .NET 数据源的数据。它可以排序和过滤数据行,使用主从关系和查找数据列。一切都可以通过点击几下鼠标来完成。 直接连接到 ADO、MS SQL 或基于 xml 的数据库。其他连接器可作为插件使用。 能够从 IEnumerable 类型的业务对象中获取数…...

unzip: cannot find zipfile directory in one of
下面是执行flutter doctor 后报错内容 End-of-central-directory signature not found. Either this file is not a zipfile, or it constitutes one disk of a multi-part archive. In the latter case the central directory and zipfile comment will be found on the last …...
;CONFIG_CRYPTO_GCM)
RFC4543: Galois Message Authentication Code (GMAC);CONFIG_CRYPTO_GCM
在2010年这个算法被Linux社区加进来:说明算法还是挺重要,普遍使用。 commit 73c89c15b959adf06366722c4be8d2eddec0a529 Author: Tobias Brunner <tobias@strongswan.org> Date: Sun Jan 17 21:52:11 2010 +1100crypto: gcm - Add RFC4543 wrapper for GCMThis patc…...
【YOLOv5】 02-标注图片,训练并使用自己的模型
在上一篇文章中,我们完成了YOLOv5的安装和测试。如果想检测自定义目标,就需要用到LabelImg来对图片打标签,本篇文章介绍了LabelImg安装与使用,以及如何训练并使用自己的模型。一、安装LabelImg输入如下命令进行安装:pi…...
)
2023.2.15日学习内容(用户的增删改查)
1,如果前端时间需要年月日,不需要时分秒,则一般情况下再数据库里面操作即可2.正常情况下,以后所有的查询都不能用* 查询所有列3.删除思路逻辑1)点击删除按钮需要对其进行监听2)对于重要的信息删除应该给用户…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库,基于 mysql 库改进而来,具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点: 支持 Promise / async-await…...
