matlab使用教程(24)—常微分方程(ODE)求解器
1.常微分方程
2.ODE 的类型
3.ODE 方程组
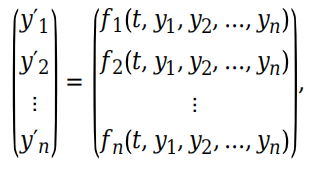
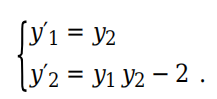
function dy = myODE(t,y)
dy(1) = y(2);
dy(2) = y(1)*y(2)-2;
end4.高阶 ODE
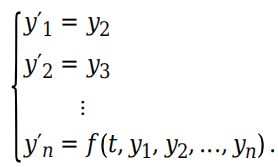
例如,考虑三阶 ODE :y′′′ − y′′y + 1 = 0,并使用代换法
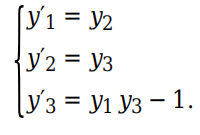
此方程组的代码则为
function dydt = f(t,y)dydt(1) = y(2);dydt(2) = y(3);dydt(3) = y(1)*y(3)-1;
end5.复数 ODE
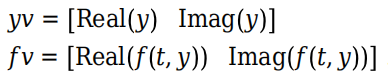
function f = complexf(t,y)
f = y.*t + 2*i;
endfunction fv = imaginaryODE(t,yv)
% Construct y from the real and imaginary components
y = yv(1) + i*yv(2);
% Evaluate the function
yp = complexf(t,y);
% Return real and imaginary in separate components
fv = [real(yp); imag(yp)];
endy0 = 1+i;
yv0 = [real(y0); imag(y0)];
tspan = [0 2];
[t,yv] = ode45(@imaginaryODE, tspan, yv0);y = yv(:,1) + i*yv(:,2);6.基本求解器选择
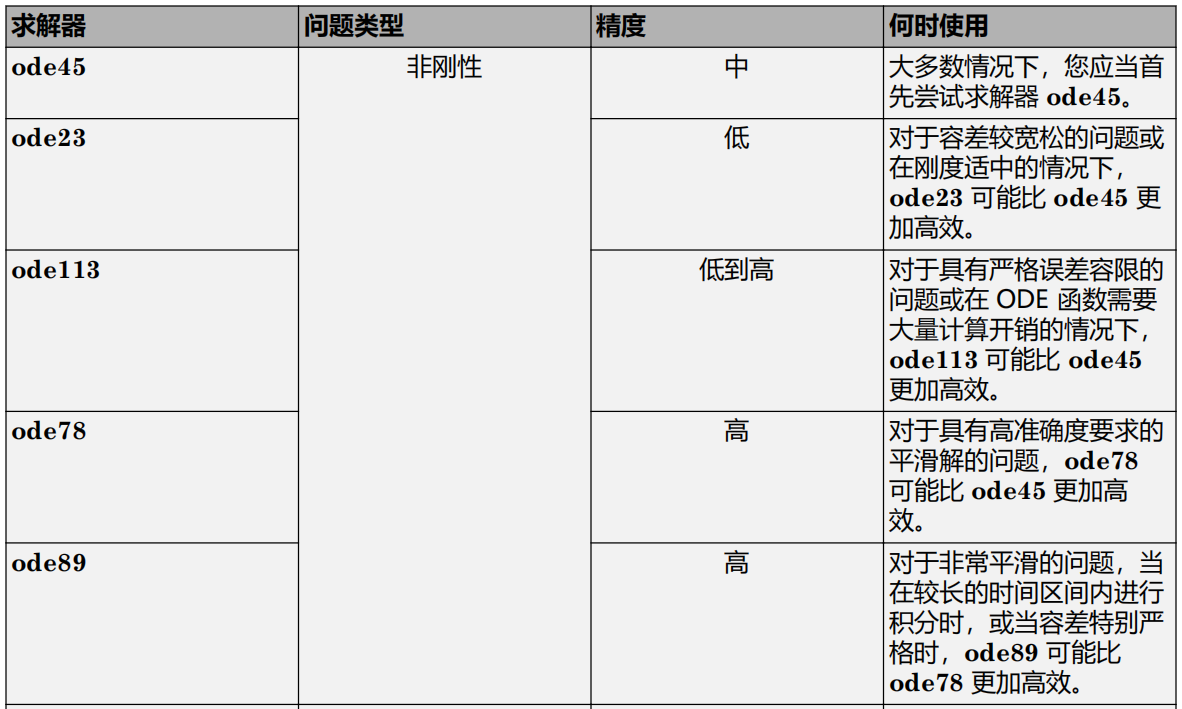
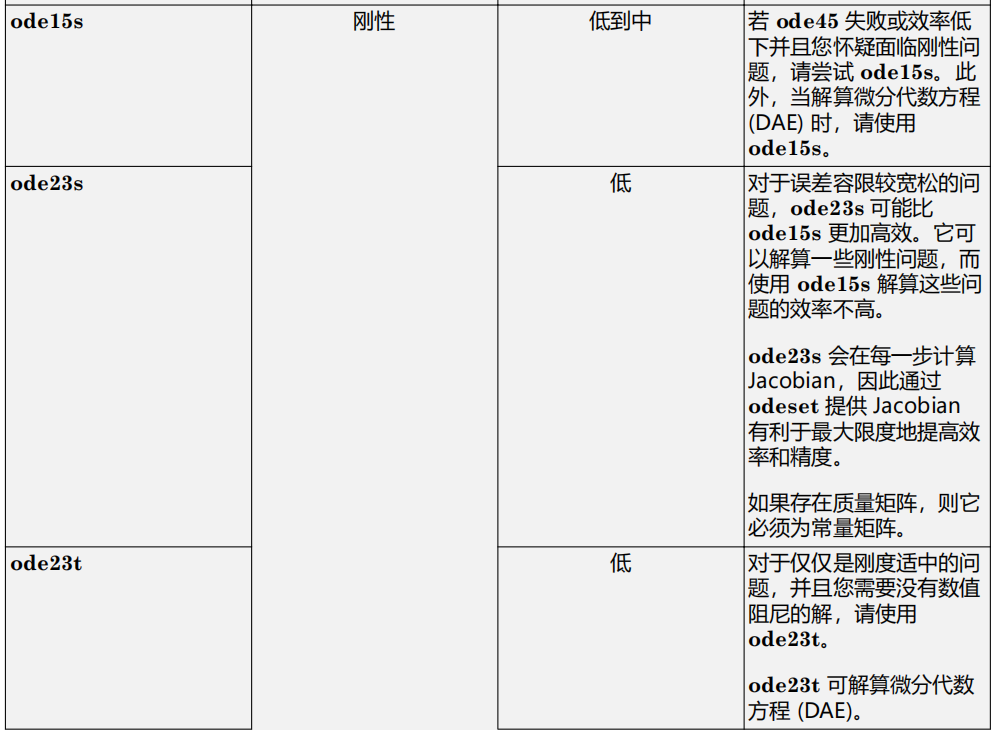

7.ODE 示例和文件摘要
odeexamplesedit exampleFileName.mexampleFileName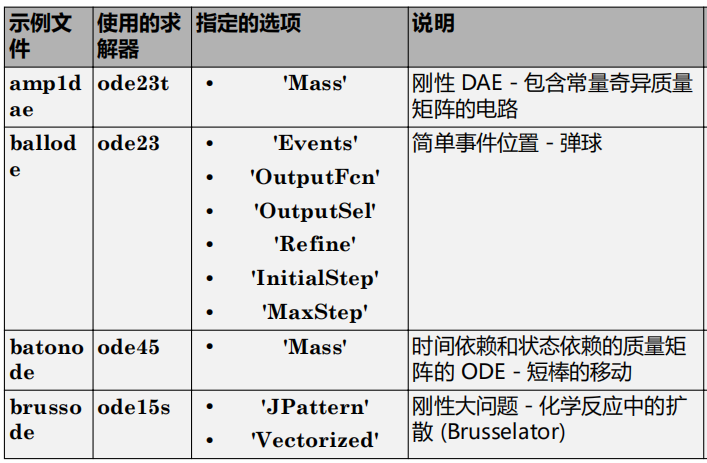
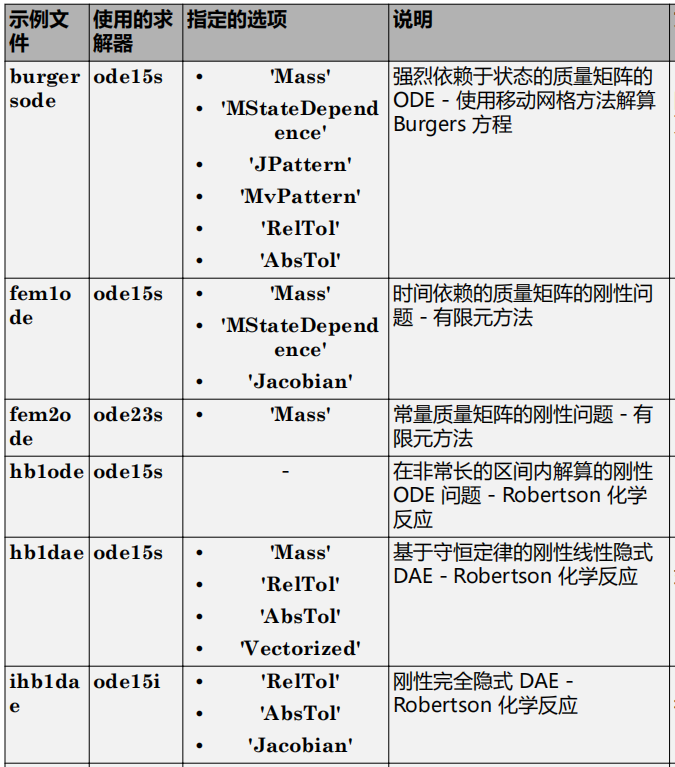

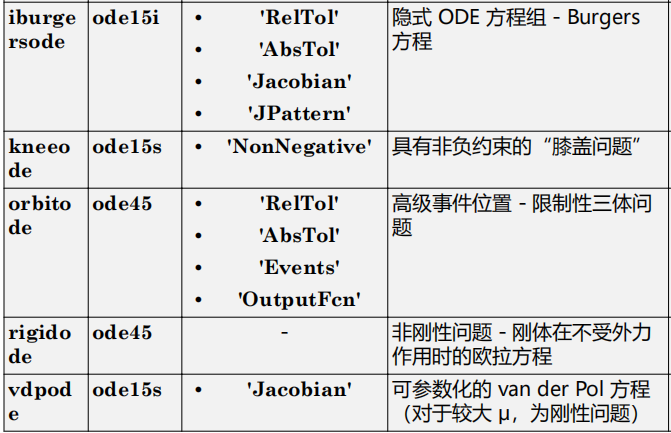
相关文章:

matlab使用教程(24)—常微分方程(ODE)求解器
1.常微分方程 常微分方程 (ODE) 包含与一个自变量 t(通常称为时间)相关的因变量 y 的一个或多个导数。此处用于表示 y 关于 t 的导数的表示法对于一阶导数为 y ′ ,对于二阶导数为 y ′′,依此类推。ODE 的阶数等于 y 在方程中…...

企业级数据共享规模化模式
数据共享正在成为企业数据战略的重要元素。对于公司而言,Amazon Data Exchange 这样的亚马逊云科技服务提供了与其他公司共享增值数据或从这些数据获利的途径。一些企业希望有一个数据共享平台,他们可以在该平台上建立协作和战略方法,在封闭、…...
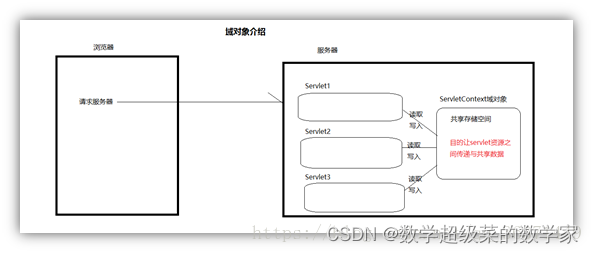
Web服务器-Tomcat详细原理与实现
Tomcat 安装与使用 :MAC 安装配置使用Tomcat - 掘金 安装后本计算机就相当于一台服务器了!!! 方式一:使用本地安装的Tomcat 1、将项目文件移动到Tomcat的webapps目录下。 2、启动Tomcat 3、在浏览器输入想要加载的…...
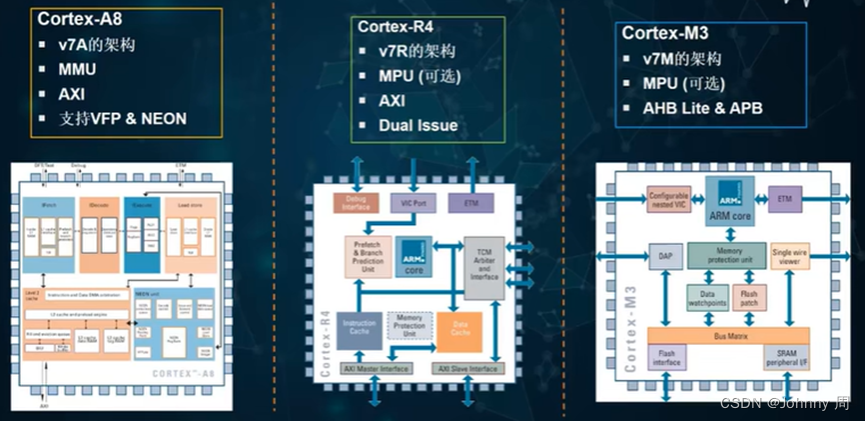
ARM处理器核心概述
一、基于ARM处理器的嵌入式系统 ARM核深度嵌入SOC中,通过JTAG口进行外部调试。计通常既有外部内存又有内部内存,从而支持不通的内存宽度、速度和大小。一般会包含一个中断控制器。可能包含一些Primece外设,需要从ARM公司取得授权。总线使用A…...
万户协同办公平台 ezoffice存在未授权访问漏洞 附POC
文章目录 万户协同办公平台 ezoffice存在未授权访问漏洞 附POC1. 万户协同办公平台 ezoffice简介2.漏洞描述3.影响版本4.fofa查询语句5.漏洞复现6.POC&EXP7.整改意见8.往期回顾 万户协同办公平台 ezoffice存在未授权访问漏洞 附POC 免责声明:请勿利用文章内的相…...
使用ctcloss训练矩阵生成目标字符串
首先我们需要明确 c t c l o s s ctcloss ctcloss是用来做什么的。比如说要生成的目标字符串长度为 l l l,而这个字符串包含 s s s个字符,字符串允许的最大长度为 L L L,这里认为一个位置是一个时间步,就是一拍,记为 T…...
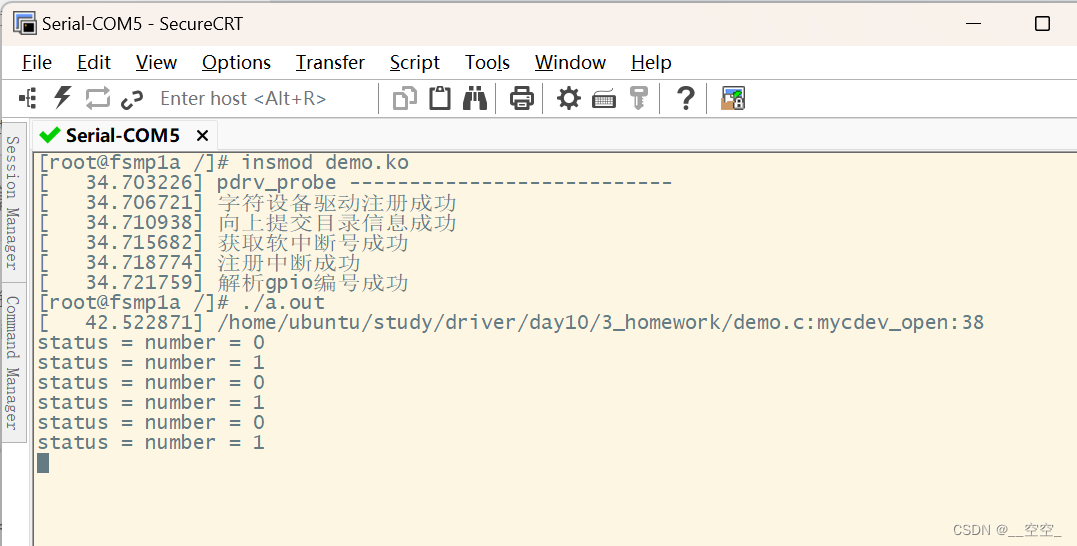
驱动 - 20230829
练习 基于platform实现 在根节点下,增加设备树 myplatform {compatible"hqyj,myplatform";interrupts-extended<&gpiof 9 0>, <&gpiof 7 0>, <&gpiof 8 0>;led1-gpio<&gpioe 10 0>;reg<0x12345678 59>;}…...

数组(个人学习笔记黑马学习)
一维数组 1、定义方式 #include <iostream> using namespace std;int main() {//三种定义方式//1.int arr[5];arr[0] 10;arr[1] 20;arr[2] 30;arr[3] 40;arr[4] 50;//访问数据元素/*cout << arr[0] << endl;cout << arr[1] << endl;cout &l…...

layui表格事件分析实例
在 layui 的表格组件中,区分表头事件和行内事件是通过事件类型(toolbar 和 tool)以及 lay-filter 值来实现的。 我们有一个表格,其中有一个工具栏按钮和操作按钮。我们将使用 layui 的 table 组件来处理这些事件。 HTML 结构&…...

Android NDK JNI与Java的相互调用
一、Jni调用Java代码 jni可以调用java中的方法和java中的成员变量,因此JNIEnv定义了一系列的方法来帮助我们调用java的方法和成员变量。 以上就是jni调用java类的大部分方法,如果是静态的成员变量和静态方法,可以使用***GetStaticMethodID、CallStaticObjectMethod等***。就…...

装备制造企业如何执行精益管理?
导 读 ( 文/ 2358 ) 精益管理是一种以提高效率、降低成本和优化流程为目标的管理方法。装备制造行业具备人工参与度高,产成品价值高,质量要求高的特点。 在装备制造企业中实施精益管理可以帮助企业提高竞争力、提升生产效率并提供高质量的产品。本文将…...

PHP8中自定义函数-PHP8知识详解
1、什么是函数? 函数,在英文中的单词是function,这个词语有功能的意思,也就是说,使用函数就是在编程的过程中,实现一定的功能。即函数就是实现一定功能的一段特定代码。 在前面的教学中,我们已…...

虚拟化技术:云计算发展的核心驱动力
文章目录 虚拟化技术的概念和作用虚拟化技术的优势虚拟化技术对未来发展的影响结论 🎉欢迎来到AIGC人工智能专栏~虚拟化技术:云计算发展的核心驱动力 ☆* o(≧▽≦)o *☆嗨~我是IT陈寒🍹✨博客主页:IT陈寒的博客🎈该系…...

光伏+旅游景区
传统化石燃料可开发量逐渐减少,并且对环境造成的危害日益突出。全世界都把目光投向了可再生能源,希望可再生能源能够改变人类的能源结构。丰富的太阳能取之不尽、用之不竭,同时对环境没有影响,光伏发电是近些年来发展最快…...
)
手搓文本向量数据库(自然语言搜索生成模型)
import paddle import jieba import pandas as pd import numpy as np import os from glob import glob from multiprocessing import Process, Manager, freeze_supportfrom tqdm import tqdm# 首先 确定的是输出的时候一定要使用pd.to_pickle() pd.read_pickle() # 计算的时…...

EVO大赛是什么
价格是你所付出的东西,而价值是你得到的东西 EVO大赛是什么? “EVO”大赛全称“Evolution Championship Series”,是北美最高规格格斗游戏比赛,大赛正式更名后已经连续举办12年,是全世界最大规模的格斗游戏赛事。常见…...

linux中使用clash代理
本机环境:ubuntu16 安装代理工具(这里使用clash) 可以手动下载解压,下载地址:https://github.com/Dreamacro/clash 也可以直接使用命令行,演示如下: userlocalhost:~$ curl https://glados.r…...
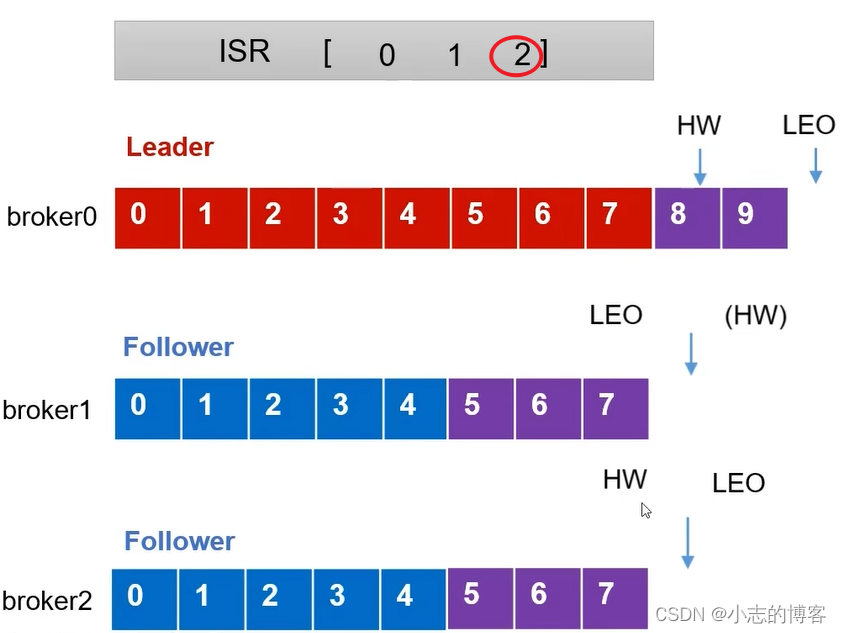
Kafka3.0.0版本——Follower故障处理细节原理
目录 一、服务器信息二、服务器基本信息及相关概念2.1、服务器基本信息2.2、LEO的概念2.3、HW的概念 三、Follower故障处理细节 一、服务器信息 三台服务器 原始服务器名称原始服务器ip节点centos7虚拟机1192.168.136.27broker0centos7虚拟机2192.168.136.28broker1centos7虚拟…...
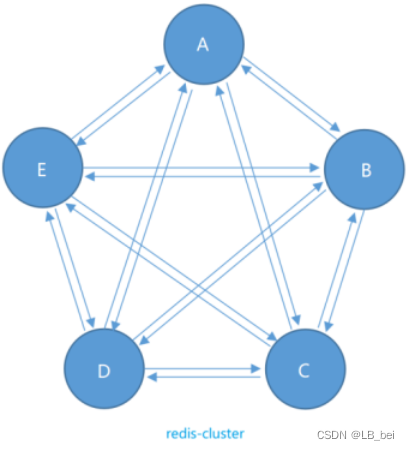
13.redis集群、主从复制、哨兵
1.redis主从复制 主从复制是指将一台redis服务器(主节点-master)的数据复制到其他的redis服务器(从节点-slave),默认每台redis服务器都是主节点,每个主节点可以有多个或没有从节点,但一个从节点…...
linux字符串处理
目录 1 C 截取字符串,截取两个子串中间的字符串2 获取该字符串后面的字符串用 strstr() 函数查找需要提取的特定字符串,然后通过指针运算获取该字符串后面的字符串用 strtok() 函数分割字符串,找到需要提取的特定字符串后,调用 strtok() 传入…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...
