约束优化:约束优化的三种序列无约束优化方法
文章目录
- 约束优化:约束优化的三种序列无约束优化方法
- 外点罚函数法
- L2-罚函数法:非精确算法
- 对于等式约束
- 对于不等式约束
- L1-罚函数法:精确算法
- 内点罚函数法:障碍函数法
- 等式约束优化问题的拉格朗日函数法:Uzawa's Method for convex optimization
- 参考文献
约束优化:约束优化的三种序列无约束优化方法
罚函数法是指将约束作为惩罚项加到目标函数中,从而转化成熟悉的无约束优化问题。
外点罚函数法
简而言之,外点罚函数法是指对于可行域外的点,惩罚项为正,即对该点进行惩罚;对于可行域内的点,惩罚项为0,即不做任何惩罚。因此,该算法在迭代过程中点列一般处于可行域之外,惩罚项会促使无约束优化问题的解落在可行域内。罚函数一般由约束部分乘正系数组成,通过增大该系数,我们可以更严厉地惩罚违反约束的行为,从而迫使惩罚函数的最小值更接近约束问题的可行区域。
L2-罚函数法:非精确算法
对于等式约束


对于不等式约束


对于一般优化问题,则是将上述不等式约束和等式约束的惩罚项加到一起。

什么情况下使用L2-罚函数法?
- 实际优化问题中,等式与不等式约束具有物理意义;
- 约束违背量不要求特别小,在1e-2~1e-3之间可接受就行。例如某优化问题中速度约束v≤10v \leq 10v≤10,解v=10.01v=10.01v=10.01也可以接受。
使用该方法时,可采用如下两种方式:
- 一步到位,即取σ\sigmaσ足够大,直接解无约束罚函数P最优化问题,此时P最优解是个近似解,与实际最优解之间的误差在可接受范围内;
- 序列迭代优化,例如:
σ=1⟹P(x,1)\sigma=1 \implies P(x,1)σ=1⟹P(x,1),解x1∗=x1x^{*}_{1}=x_1x1∗=x1;
σ=10⟹P(x,10)\sigma=10 \implies P(x,10)σ=10⟹P(x,10),上一次迭代x1x_1x1作初值解x2∗=x2x^{*}_{2}=x_2x2∗=x2;
σ=100⟹P(x,100)\sigma=100 \implies P(x,100)σ=100⟹P(x,100),上一次迭代x2x_2x2作初值解x3∗=x3x^{*}_{3}=x_3x3∗=x3;
……直到达到收敛准则。算法伪代码如下:

一般情况下,具体选择何种方式取决于实际工程问题的精度需求和速度需求。
L2-罚函数法的优缺点?
优点:
- 将约束优化问题转化为无约束优化问题,当ci(x)c_i(x)ci(x)光滑时可以调用一般的无约束光滑优化问题算法求解;
- 二次罚函数形式简洁直观而在实际中广泛使用。
缺点:
- 需要σ→∞\sigma \rightarrow \inftyσ→∞,此时海瑟矩阵条件数过大,对于无约束优化问题的数值方法拟牛顿法与共轭梯度法存在数值困难,且需要多次迭代求解子问题;
- 对于存在不等式约束的P(x,σ)P(x,\sigma)P(x,σ)可能不存在二次可微性质,光滑性降低;
- 不精确,与原问题最优解存在距离。
例子:
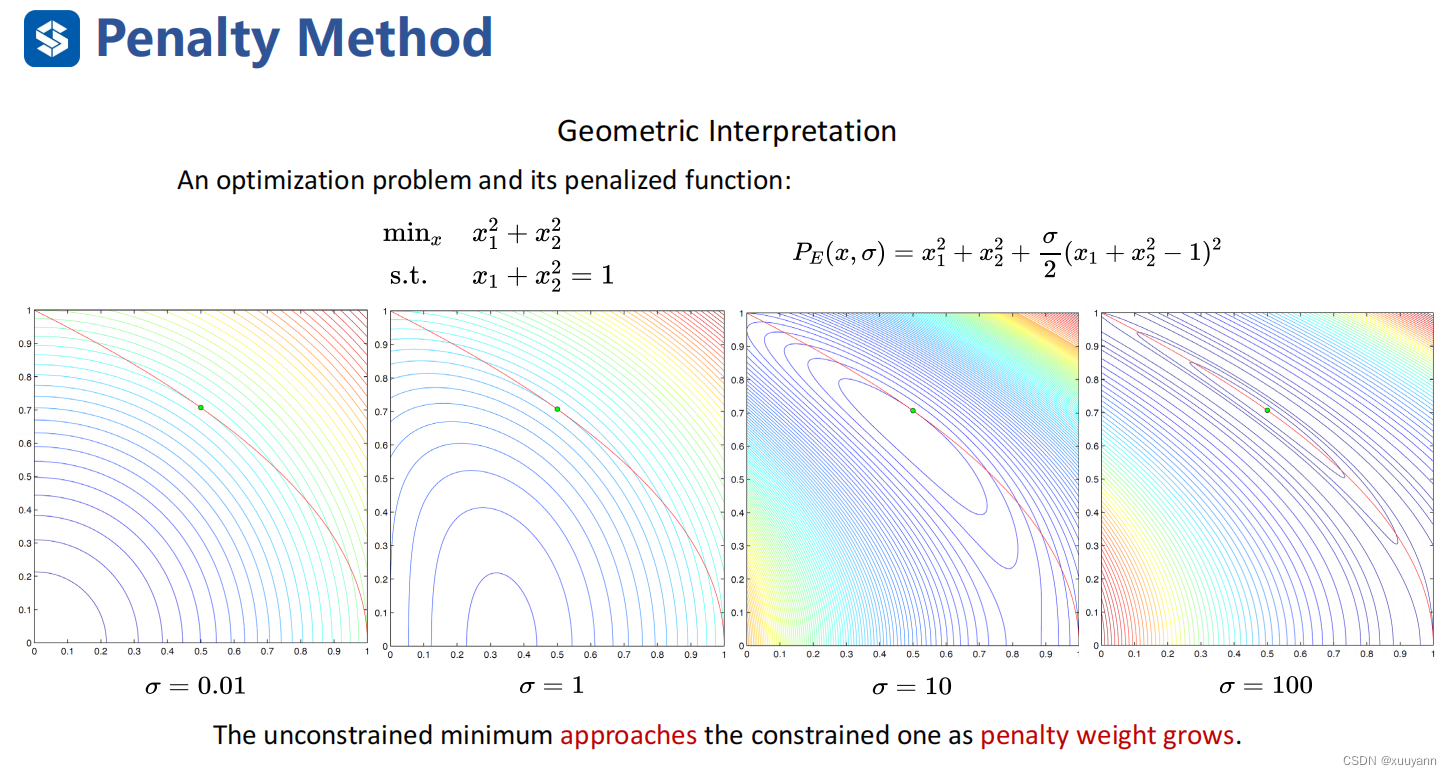
L1-罚函数法:精确算法
由于L2-罚函数法存在数值困难,并且与原问题的解存在误差,因此考虑精确罚函数法。精确罚函数是一种问题求解时不需要令罚因子趋于正无穷(或零)的罚函数。换句话说,若罚因子选取适当,对罚函数进行极小化得到的解恰好就是原问题的精确解。这个性质在设计算法时非常有用,使用精确罚函数的算法通常会有比较好的性质。
由于L1-罚函数非光滑,因此无约束优化问题P的收敛速度无法保证,这实际上就相当于用牺牲收敛速度的方式来换取优化问题P的精确最优解。

内点罚函数法:障碍函数法
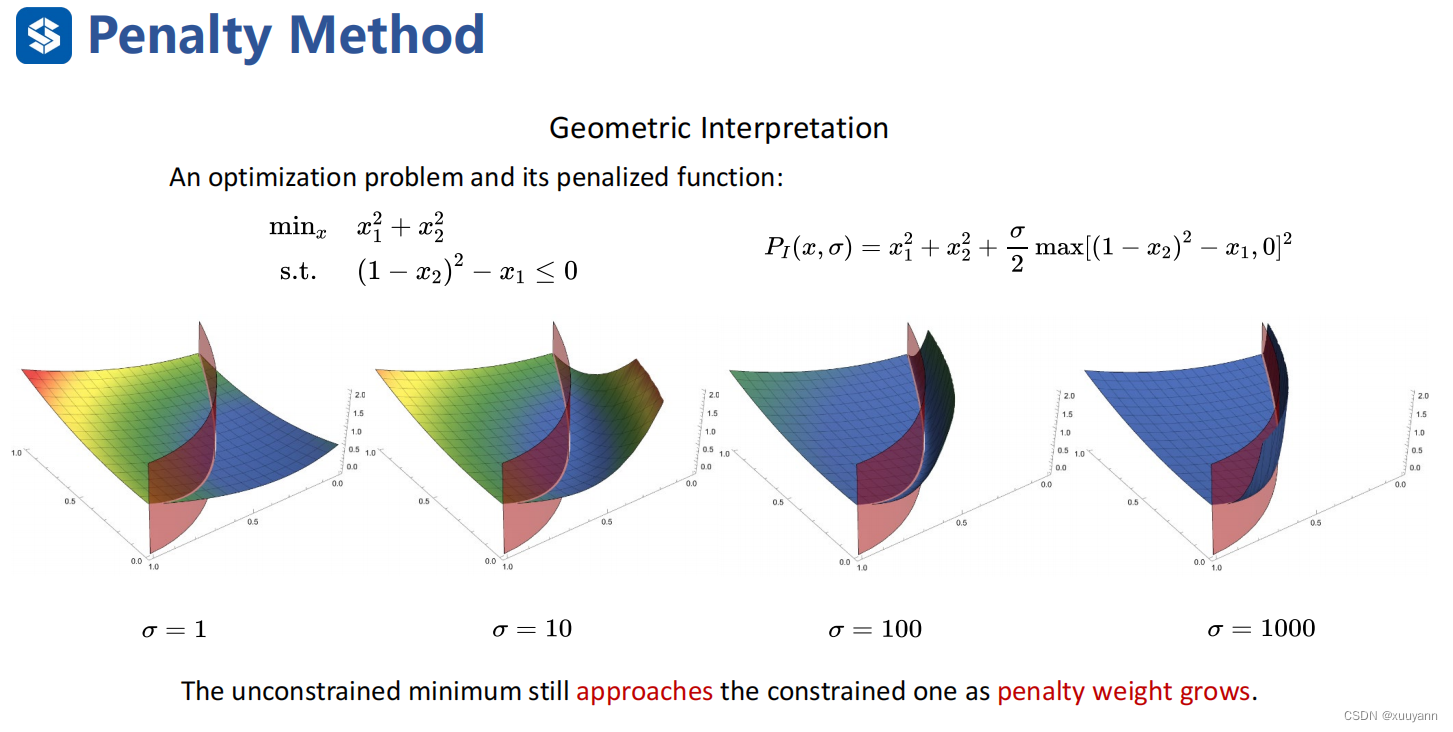
前面介绍的L1和L2罚函数均属于外点罚函数,即在求解过程中允许自变量xxx位于原问题可行域之外,当罚因子趋于无穷时,子问题最优解序列从可行域外部逼近最优解。自然地,如果我们想要使得子问题最优解序列从可行域内部逼近最优解,则需要构造内点罚函数。顾名思义,内点罚函数在迭代时始终要求自变量xxx不能违反约束,因此它主要用于不等式约束优化问题。
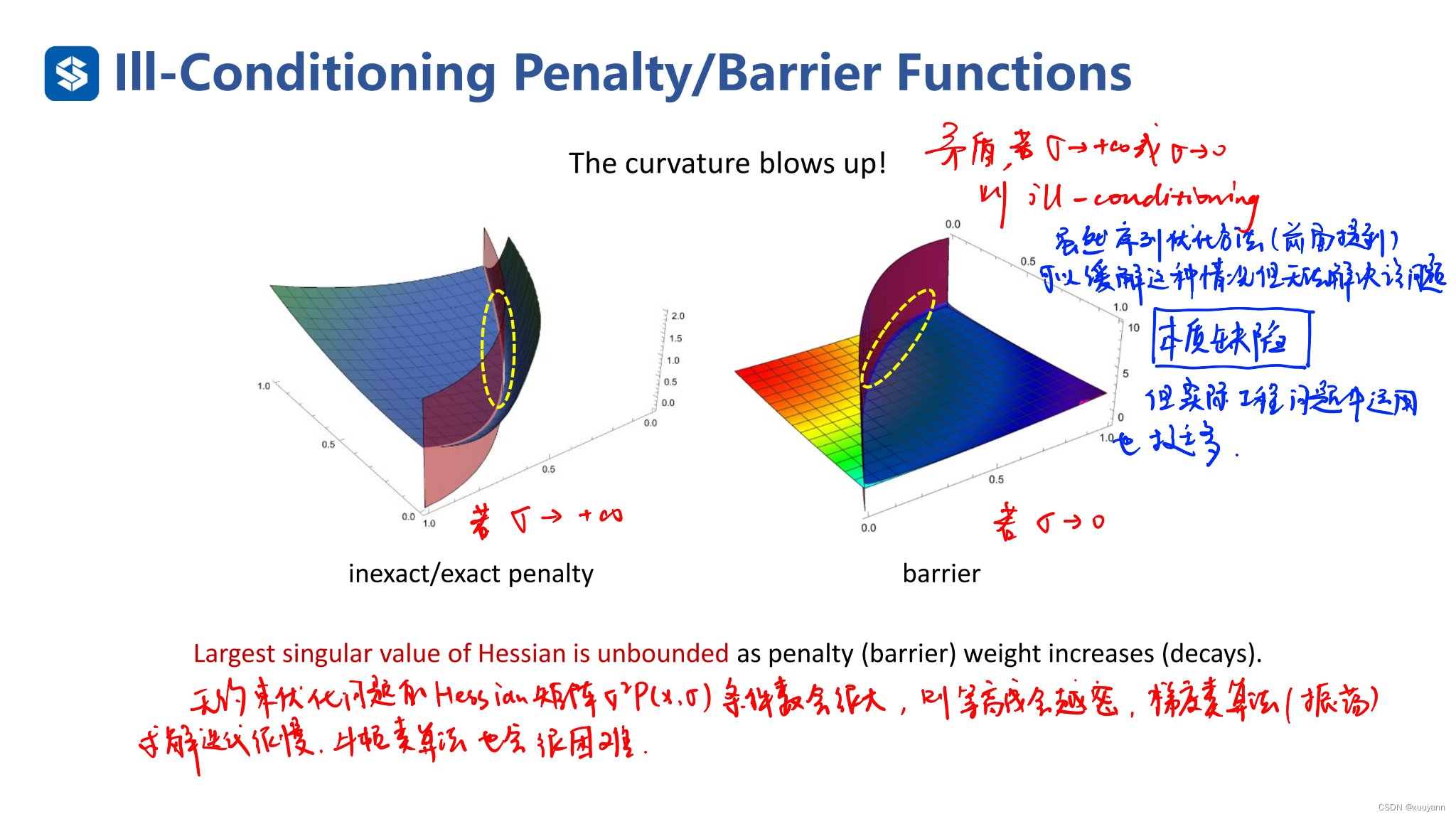
如下图所示,考虑含不等式约束的优化问题,为了使迭代点始终在可行域内,当迭代点趋于可行域边界时,我们需要罚函数趋于正无穷。常见的罚函数有三种:对数罚函数,逆罚函数和指数罚函数。对于原问题,它的最优解通常位于可行域边界,即ci(x)≤0c_i(x) \leq 0ci(x)≤0中至少有一个取到等号,此时需要调整惩罚因子σ\sigmaσ使其趋于0,这会减弱障碍罚函数在边界附近的惩罚效果。

算法伪代码如下:

同样地,内点罚函数法也会有类似外点罚函数法的数值困难,即当σ\sigmaσ趋于0时,子问题P(x,σ)P(x,\sigma)P(x,σ)的海瑟矩阵条件数会趋于无穷,因此对子问题的求解将会越来越困难。
等式约束优化问题的拉格朗日函数法:Uzawa’s Method for convex optimization
基础预备:
凸优化学习笔记(一)
凸优化学习笔记:Lagrange函数、对偶函数、对偶问题、KKT条件
多元函数的极值和鞍点
**若原问题是凸问题,则KKT条件是充要条件。**原问题连续凸则拉格朗日函数严格凸,原问题的最优值p∗p^*p∗与对偶问题的最优值d∗d^*d∗相等,(x∗,λ∗)(x^*,\lambda ^*)(x∗,λ∗)是拉格朗日函数的鞍点,同时也是原问题和对偶问题的最优解。


综上分析,Uzawa’s Method迭代过程分为两个步骤:
{xk+1=argminxL(x,λk)λk+1=λk+α(Axk+1−b)\left\{\begin{array}{l} x^{k+1}=\underset{x}{\operatorname{argmin}} \mathcal{L}\left(x, \lambda^k\right) \\ \lambda^{k+1}=\lambda^k+\alpha\left(A x^{k+1}-b\right) \end{array}\right. {xk+1=xargminL(x,λk)λk+1=λk+α(Axk+1−b)
(1)给定λk\lambda^kλk,求解minxL(x,λk)\min _x \mathcal{L}(x, \lambda^k)minxL(x,λk)无约束优化问题,求解得到xk+1x^{k+1}xk+1;
(2)更新λ\lambdaλ,L(xk+1,λ)L(x^{k+1},\lambda)L(xk+1,λ)关于λ\lambdaλ的梯度为∂L∂λ∣x+1=Axk+1−b\left.\frac{\partial L}{\partial \lambda}\right|_{x+1}=A x^{k+1}-b∂λ∂Lx+1=Axk+1−b,若要求解maxλL(xk+1,λ)\max _\lambda \mathcal{L}(x^{k+1}, \lambda)maxλL(xk+1,λ),则沿着梯度上升方向进入步长迭代,即λk+1=λk+α(Axk+1−b)\lambda^{k+1}=\lambda^k+\alpha\left(A x^{k+1}-b\right)λk+1=λk+α(Axk+1−b),α\alphaα为迭代步长。
该方法的前提就是原函数连续凸,L(x,λ)\mathcal L(x,\lambda)L(x,λ)关于xxx严格凸,则minxL(x,λk)\min _x \mathcal{L}(x, \lambda^k)minxL(x,λk)只存在一个最优解,可求出唯一xk+1x^{k+1}xk+1进而更新λk+1\lambda^{k+1}λk+1,否则xk+1x^{k+1}xk+1会存在多个,不知道选择哪个去更新λ\lambdaλ。因此缺点很明显,该方法要求原函数必须为连续凸函数,梯度上升步长需要调整且收敛速率不能保证。
参考文献
机器人中的数值优化
最优化:建模、算法与理论/最优化计算方法
相关文章:

约束优化:约束优化的三种序列无约束优化方法
文章目录约束优化:约束优化的三种序列无约束优化方法外点罚函数法L2-罚函数法:非精确算法对于等式约束对于不等式约束L1-罚函数法:精确算法内点罚函数法:障碍函数法等式约束优化问题的拉格朗日函数法:Uzawas Method fo…...

RocketMQ快速入门:消息发送、延迟消息、消费重试
一起学编程,让生活更随和! 如果你觉得是个同道中人,欢迎关注博主gzh:【随和的皮蛋桑】。 专注于Java基础、进阶、面试以及计算机基础知识分享🐳。偶尔认知思考、日常水文🐌。 目录1、RocketMQ消息结构1.1…...
FANUC机器人通过KAREL程序实现与PLC位置坐标通信的具体方法示例
FANUC机器人通过KAREL程序实现与PLC位置坐标通信的具体方法示例 在通信IO点位数量足够的情况下,可以使用机器人的IO点传输位置数据,这里以传输机器人的实时位置为例进行说明。 基本流程如下图所示: 基本步骤可参考如下: 首先确认机器人控制柜已经安装了总线通信软件(例如…...

[蓝桥杯 2015 省 B] 移动距离
蓝桥杯 2015 年省赛 B 组 H 题题目描述X 星球居民小区的楼房全是一样的,并且按矩阵样式排列。其楼房的编号为 1,2,3,⋯ 。当排满一行时,从下一行相邻的楼往反方向排号。比如:当小区排号宽度为 6 时,开始情形如下:我们的…...
Pandas库入门仅需10分钟
数据处理的时候经常性需要整理出表格,在这里介绍pandas常见使用,目录如下: 数据结构导入导出文件对数据进行操作 – 增加数据(创建数据) – 删除数据 – 改动数据 – 查找数据 – 常用操作(转置࿰…...

python的socket通信中,如何设置可以让两台主机通过外网访问?
要让两台主机通过外网进行Socket通信,需要在网络设置和代码实现两个方面进行相应的配置。下面是具体的步骤: 确认网络环境:首先要确保两台主机都能够通过外网访问。可以通过ping命令或者telnet命令来测试两台主机之间是否可以互相访问。 确定…...
)
检测数据的方法(回顾)
检测数据类型的4种方法typeofinstanceofconstructor{}.toString.call() 检测数据类型的4种方法 typeof 定义 用来检测数据类型的运算符 返回一个字符串,表示操作值的数据类型(7种) number,string,boolean,object,u…...
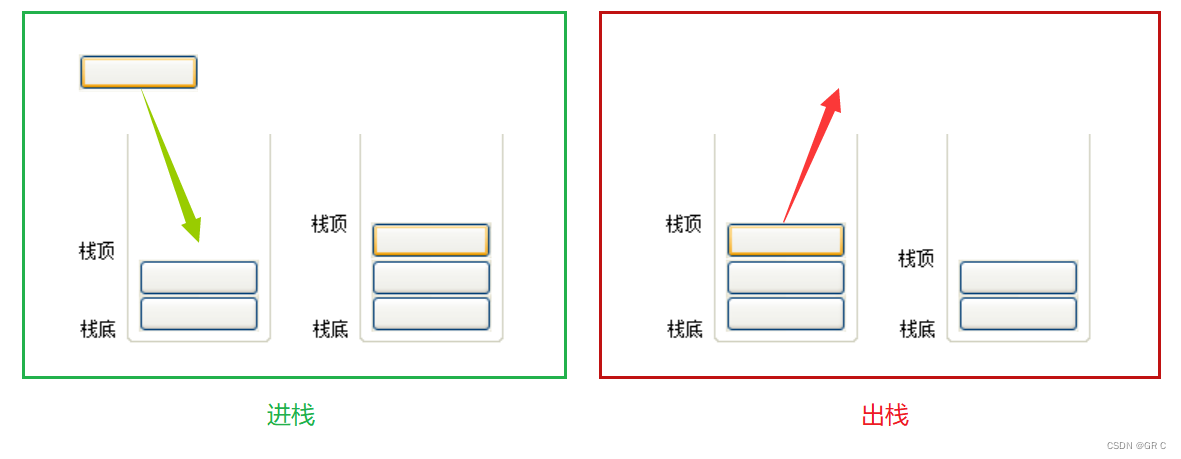
比特数据结构与算法(第三章_上)栈的概念和实现(力扣:20. 有效的括号)
一、栈(stack)栈的概念:① 栈是一种特殊的线性表,它只允许在固定的一端进行插入和删除元素的操作。② 进行数据插入的删除和操作的一端,称为栈顶 。另一端则称为 栈底 。③ 栈中的元素遵守后进先出的原则,即…...
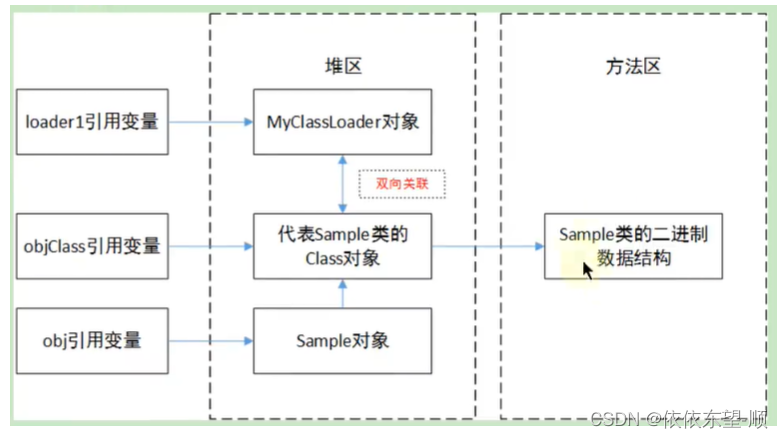
JVM13 类的生命周期
1. 概述 在 Java 中数据类型分为基本数据类型和引用数据类型。基本数据类型由虚拟机预先定义,引用数据类型则需要进行类的加载。 按照 Java 虚拟机规范,从 class 文件到加载到内存中的类,到类卸载出内存为止,它的整个生命周期包…...
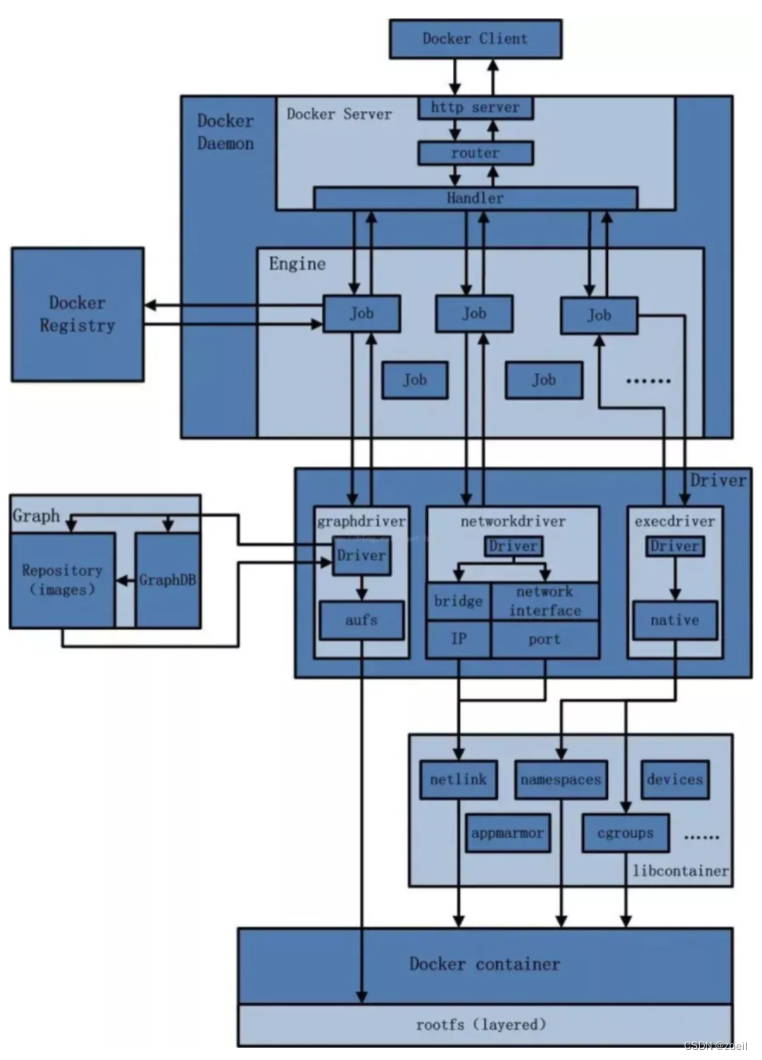
Docker网络模式解析
目录 前言 一、常用基本命令 (一)查看网络 (二)创建网络 (三)查看网络源数据 (四)删除网络 二、网络模式 (一)总体介绍 (二)…...

游山城重庆
山城楼梯多,路都是上坡。 为了赶早上8点从成都到重庆的动车,凌晨5点半就爬起床来,由于昨天喝了咖啡,所以我将尽3点才睡觉,这意味着我只睡了2个多小时。起来简单休息之后,和朋友协商好时间就一起出门了。 …...

Vuex的创建和简单使用
Vuex 1.简介 1.1简介 1.框框里面才是Vuex state:状态数据action:处理异步mutations:处理同步,视图可以同步进行渲染1.2项目创建 1.vue create 名称 2.运行后 3.下载vuex。采用的是基于vue2的版本。 npm install vuex3 --save 4.vu…...

Arduino IDE搭建Heltec开发板开发环境
Arduino IDE搭建Heltec开发板开发环境Heltec开发板开发环境下载与搭建Arduino IDE下载与安装搭建Heltec开发板的开发环境添加package URL方法通过Git的方法安装离线安装Heltec开发板开发环境下载与搭建 Arduino IDE下载与安装 Heltec的ESP系列和大部分的LoRa系列开发板都是用A…...

Using the GNU Compiler Collection 目录翻译
文章目录Introduction1 Programming Languages Supported by GCC2 Language Standards Supported by GCC2.1 C Language3 GCC Command Options3.1 Option Summary4 C Implementation-Defined Behavior6 Extensions to the C Language Family9 Binary Compatibility其他工具10 g…...

使用 OpenCV for Android 进行图像特征检测
android 开发人员,可能熟悉使用activities, fragments, intents以及最重要的一系列开源依赖库。但是,注入需要本机功能的依赖关系(如计算机视觉框架)并不像在 gradle 文件中直接添加实现语句那样简单!今天,将专注于使用 OpenCV 库…...
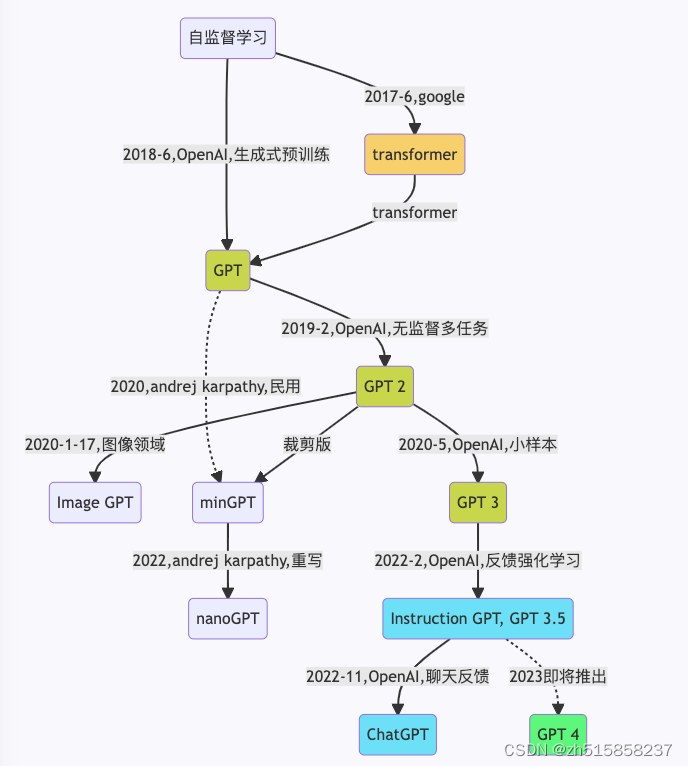
chatGPT笔记
文章目录 一、GPT之技术演进时间线二、chatGPT中的语言模型instructGPT跟传统语言LM模型最大不同点是什么?三、instructGPT跟GPT-3的网络结构是否一样四、GPT和BERT有啥区别五、chatGPT的训练过程是怎样的?六、GPT3在算数方面的能力七、GPT相比于bert的优点是什么八、元学习(…...

这么好的政策和创新基地,年轻人有梦想你就来
周末有空去参观了下一个朋友办的公司。位置和环境真不错,且租金低的离谱,半年租金才2000元,且提供4个工位。这个创新基地真不赖啊,国家鼓励创新创业,助力年轻人实现梦想。场地有办公区,休息区应有尽有&…...
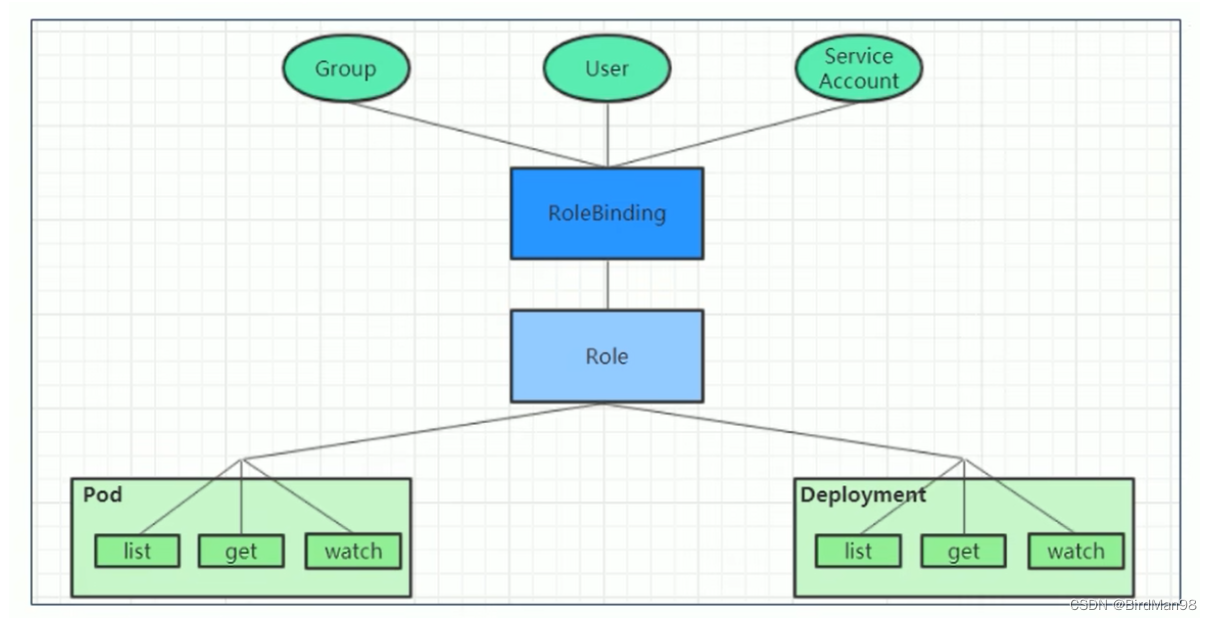
【Kubernetes】【十九】安全认证
第九章 安全认证 本章节主要介绍Kubernetes的安全认证机制。 访问控制概述 Kubernetes作为一个分布式集群的管理工具,保证集群的安全性是其一个重要的任务。所谓的安全性其实就是保证对Kubernetes的各种客户端进行认证和鉴权操作。 客户端 在Kubernetes集群…...

Apache Flink 实时计算在美的多业务场景下的应用与实践
摘要:本文整理自美的集团实时数据负责人、资深数据架构师董奇,在 Flink Forward Asia 2022 主会场的分享。本篇内容主要分为四个部分: 实时生态系统在美的的发展和建设现状 核心传统业务场景 Flink 实时数字化转型实践 新兴业务场景 Flink …...

27 pandas 数据透视
文章目录pivot_table 函数1、index需要聚合的列名,默认情况下聚合所有数据值的列2、values在结果透视的行上进行分组的列名或其它分组键【就是透视表里显示的列】3、columns在结果透视表的列上进行分组的列名或其它分组键4、Aggfunc聚合函数或函数列表(默…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...
