C语言每日一练------Day(5)
本专栏为c语言练习专栏,适合刚刚学完c语言的初学者。本专栏每天会不定时更新,通过每天练习,进一步对c语言的重难点知识进行更深入的学习。
今日练习题关键字:错误的集合 密码检查

💓博主csdn个人主页:小小unicorn
⏩专栏分类:C语言天天练
🚚代码仓库:小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识
Day1
- 题目一:
- 题目描述:
- 解题思路:
- 代码实现:
- 结果情况:
- 题目二:
- 题目描述:
- 解题思路:
- 代码实现:
- 结果情况:
- 总结:
题目一:
题目描述:
题目来源:错误的集合
集合 s 包含从 1 到 n 的整数。不幸的是,因为数据错误,导致集合里面某一个数字复制了成了集合里面的另外一个数字的值,导致集合 丢失了一个数字 并且 有一个数字重复 。
给定一个数组 nums 代表了集合 S 发生错误后的结果。
请你找出重复出现的整数,再找到丢失的整数,将它们以数组的形式返回。

解题思路:
将数组排序之后,比较每对相邻的元素,即可找到错误的集合。
寻找重复的数字较为简单,如果相邻的两个元素相等,则该元素为重复的数字。
寻找丢失的数字相对复杂,可能有以下两种情况:
1.如果丢失的数字大于 111 且小于 nnn,则一定存在相邻的两个元素的差等于 222,这两个元素之间的值即为丢失的数字;
2.如果丢失的数字是 111 或 nnn,则需要另外判断。
为了寻找丢失的数字,需要在遍历已排序数组的同时记录上一个元素,然后计算当前元素与上一个元素的差。考虑到丢失的数字可能是 111,因此需要将上一个元素初始化为 000。
1.当丢失的数字小于 nnn 时,通过计算当前元素与上一个元素的差,即可得到丢失的数字;
2.如果 nums[n−1]≠n则丢失的数字是 nnn。
代码实现:
int cmp(int* a, int* b)
{return *a - *b;
}int* findErrorNums(int* nums, int numsSize, int* returnSize)
{int* errorNums = malloc(sizeof(int) * 2);*returnSize = 2;qsort(nums, numsSize, sizeof(int), cmp);int prev = 0;for (int i = 0; i < numsSize; i++) {int curr = nums[i];if (curr == prev) {errorNums[0] = prev;} else if (curr - prev > 1) {errorNums[1] = prev + 1;}prev = curr;}if (nums[numsSize - 1] != numsSize) {errorNums[1] = numsSize;}return errorNums;
}结果情况:
符合题目要求,问题得到解决。
题目二:
题目描述:
题目来源:密码检查
小明同学最近开发了一个网站,在用户注册账户的时候,需要设置账户的密码,为了加强账户的安全性,小明对密码强度有一定要求:
- 密码只能由大写字母,小写字母,数字构成;
- 密码不能以数字开头;
- 密码中至少出现大写字母,小写字母和数字这三种字符类型中的两种;
- 密码长度至少为8
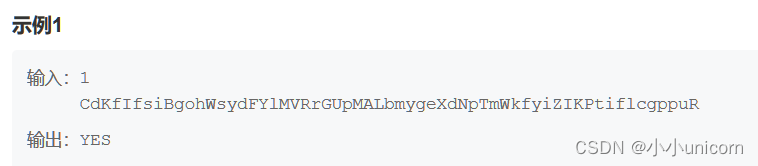
现在小明受到了n个密码,他想请你写程序判断这些密码中哪些是合适的,哪些是不合法的。
输入描述:
输入一个数n,接下来有n(n≤100)行,每行一个字符串,表示一个密码,输入保证字符串中只出现大写字母,小写字母和数字,字符串长度不超过100。
输出描述:
输入n行,如果密码合法,输出YES,不合法输出NO
解题思路:
这道题的关键就是判断字符串长度和首元素即可。
代码实现:
#include<stdio.h>
#include<string.h>int main()
{char arr[101] = { 0 };int n = 0;scanf("%d", &n);int i = 0;int j = 0;//控制总输入次数for (i = 0; i < n; i++){int flag = 0;int flag1 = 0;int flag2 = 0;scanf("%s", arr);int sz = strlen(arr);//判断字符串长度和首元素if(arr[0] >= '0' && arr[0] <= '9' || sz < 8){printf("NO\n");continue;}//判断条件1,3for (j = 0; j < sz; j++){if (arr[j] >= 'a' && arr[j] <= 'z')flag = 1;else if (arr[j] >= 'A' && arr[j] <= 'Z')flag1 = 1;else if (arr[j] >= '0' && arr[j] <= '9')flag2 = 1;else{printf("NO\n");continue;}}if (flag + flag1 + flag2 >= 2)printf("YES\n");}return 0;
}
结果情况:
符合题目要求,问题得到解决。
总结:
文章到这里就要告一段落了,有更好的想法或问题,欢迎评论区留言。
希望今天的练习能对您有所收获,咱们下期见!
相关文章:

C语言每日一练------Day(5)
本专栏为c语言练习专栏,适合刚刚学完c语言的初学者。本专栏每天会不定时更新,通过每天练习,进一步对c语言的重难点知识进行更深入的学习。 今日练习题关键字:错误的集合 密码检查 💓博主csdn个人主页:小小u…...
(Windows )本地连接远程服务器(Linux),免密码登录设置
在使用VScode连接远程服务器时,每次打开都要输入密码,以及使用ssh登录或其它方法登录,都要本地输入密码,这大大降低了使用感受,下面总结了免密码登录的方法,用起来巴适得很,起飞。 目录 PowerSh…...

Python 面试:异常处理机制
格式: 继承Exception实现自定义异常。 注意:这里是继承Exception类,而不是BaseException类,因为继承BaseException可能会导致捕获不到自定义异常。 class MyException(Exception):passtry:raise MyException(my salary is too…...

Matlab图像处理-水平镜像
镜像变换 镜像变换又常称为对称变换,它可以分为水平对称、垂直对称等多种变换。对称变换后,图像的宽和高不变。 图像的镜像分为两种垂直镜像和水平镜像。 水平镜像即将图像左半部分和右半部分以图像竖直中轴线为中心轴进行对换; 竖直镜像…...
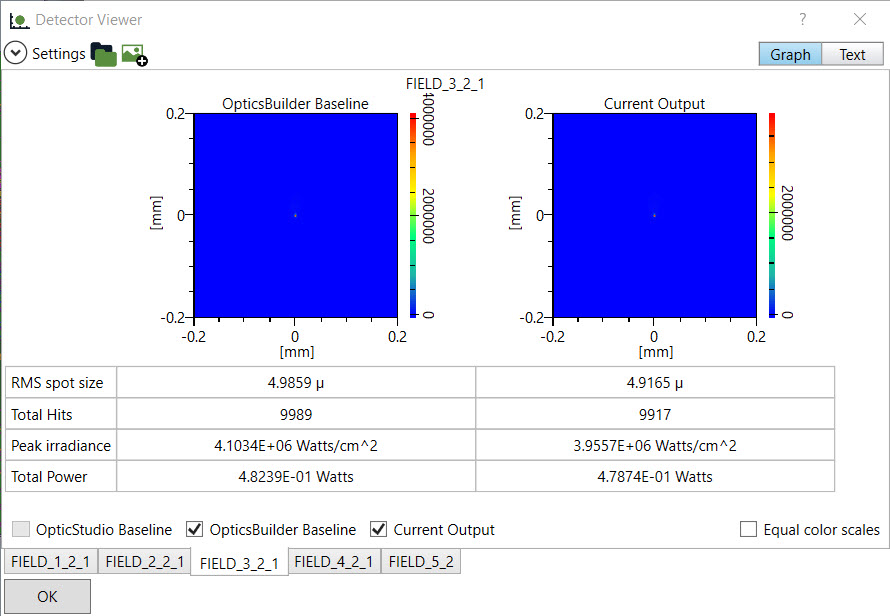
Ansys Zemax | 手机镜头设计 - 第 2 部分:使用 OpticsBuilder 实现光机械封装
本文是3篇系列文章的一部分,该系列文章将讨论智能手机镜头模块设计的挑战,从概念、设计到制造和结构变形的分析。本文是三部分系列的第二部分。概括介绍了如何在 CAD 中编辑光学系统的光学元件以及如何在添加机械元件后使用 Zemax OpticsBuilder 分析系统…...

【GPT,Flask】用Python Flask结合OpenAI的GPT API构建一个可自主搭建的内容生成应用网站
【背景】 自己构建模型并进行训练需要很高的知识,技能和资源门槛。如今,通过OpenAI提供的API,则可以快速通过GPT能力构建可以提供内容生成服务的在线网站。这套框架可以提供给用户,用户可以利用该框架在自己的环境(比如自己的公司内)构建内容生成服务。你也可以自己上线…...

vue + electron
node 版本 v14.19.3 npm 版本 6.14.17 要是node-sass报错执行命令: npm uninstall node-sass sass-loader npm i node-sass4.14.1 sass-loader7.3.1 --save -dev首先安装依赖 npm install electron npm install electron-packagerelectronRun.js放在根目录下 con…...

spring中LocalDateTime 转成字符串的时候注意事项
ApiOperation("查询课程发布信息") ResponseBody GetMapping("/r/coursepublish/{courseId}") public CoursePublish getCoursepublish(PathVariable("courseId") Long courseId) { CoursePublish coursePublish coursePublishService.getC…...

vue数组对象中按某一字段排序
给下列数组字段中的month排序 第一步:methods中写一个方法如下: sortBy(attr, rev) {//第二个参数没有传递 默认升序排列if(rev undefined) {rev 1;} else {rev (rev) ? 1 : -1;}return function(a, b) {a a[attr];b b[attr];if(a < b) {retu…...

yolov5和yolov7部署的研究
1.结论 onnx推理比torch快3倍, openvino比onnx快一丢丢。 | yolov7.pt 转 onnx python export.py --weights best_31.pt --grid --end2end --simplify --topk-all 10 --iou-thres 0.65 --conf-thres 0.65 --img-size 320 320 --max-wh 200可以看到yolov7的 onnx是包括nms…...
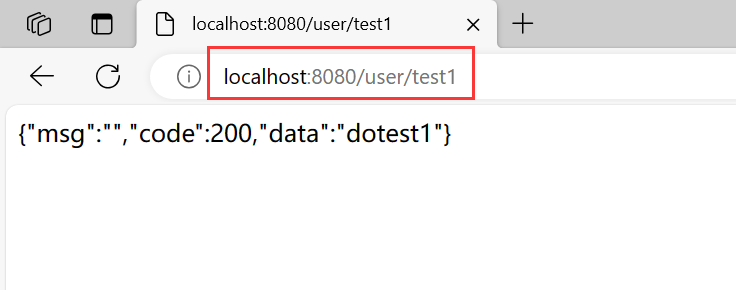
【JavaEE进阶】拦截器与统一功能处理
文章目录 一. 用户登录权限效验1. 最初用户登录验证2. Spring AOP 用户统一登录的验证3. Spring拦截器3.1 自定义拦截器3.2 将自定义拦截器设置到当前的项目中 4. 拦截器实现的原理 二. 统一的异常处理1. 统一的异常处理优点2. 统一的异常处理实现 三. 统一数据返回格式1. 统一…...
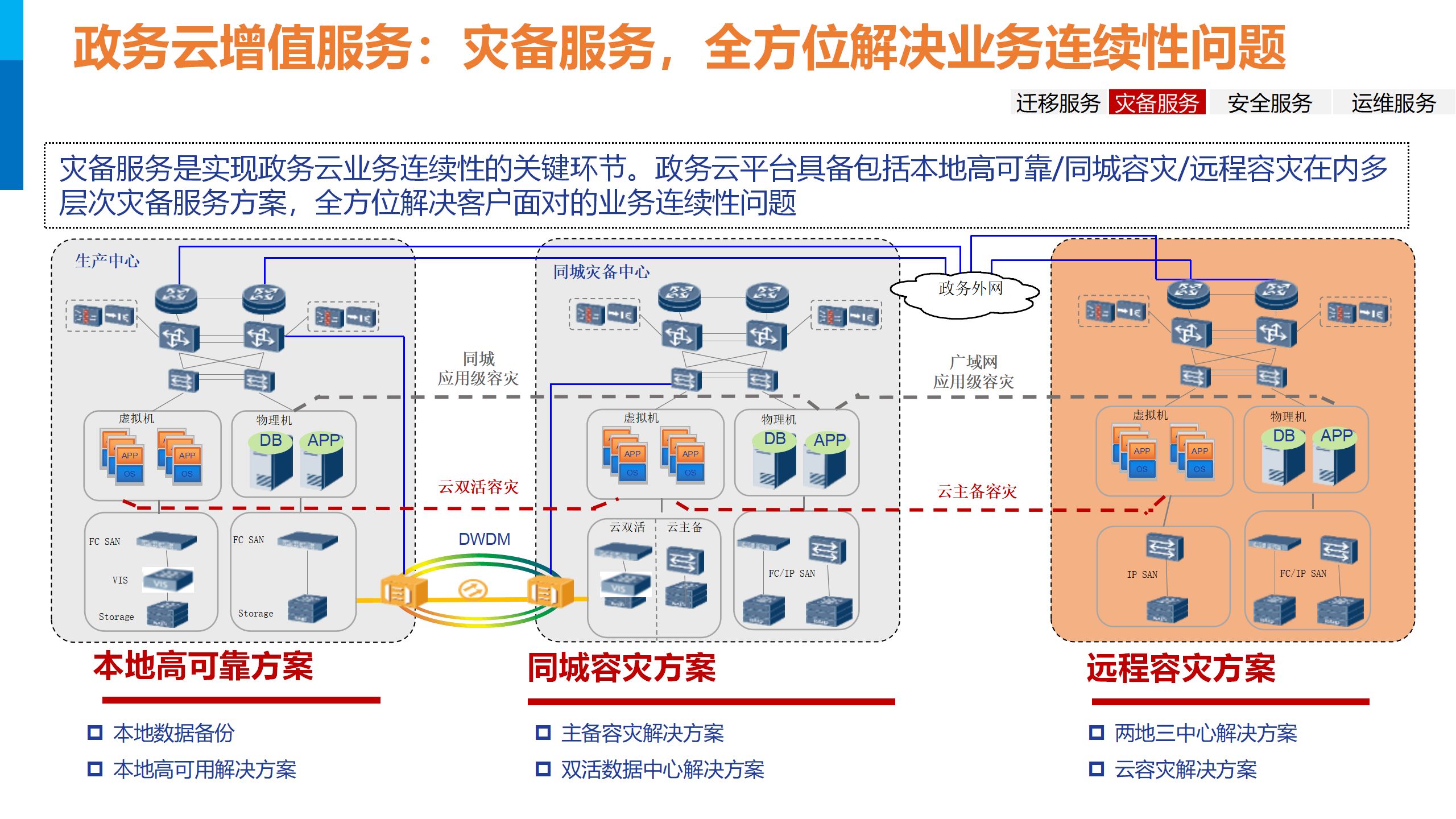
2023年智慧政务一网通办云平台顶层设计与建设方案PPT
导读:原文《2023年智慧政务一网通办云平台顶层设计与建设方案PPT》(获取来源见文尾),本文精选其中精华及架构部分,逻辑清晰、内容完整,为快速形成售前方案提供参考。 部分内容: 喜欢文章&#…...
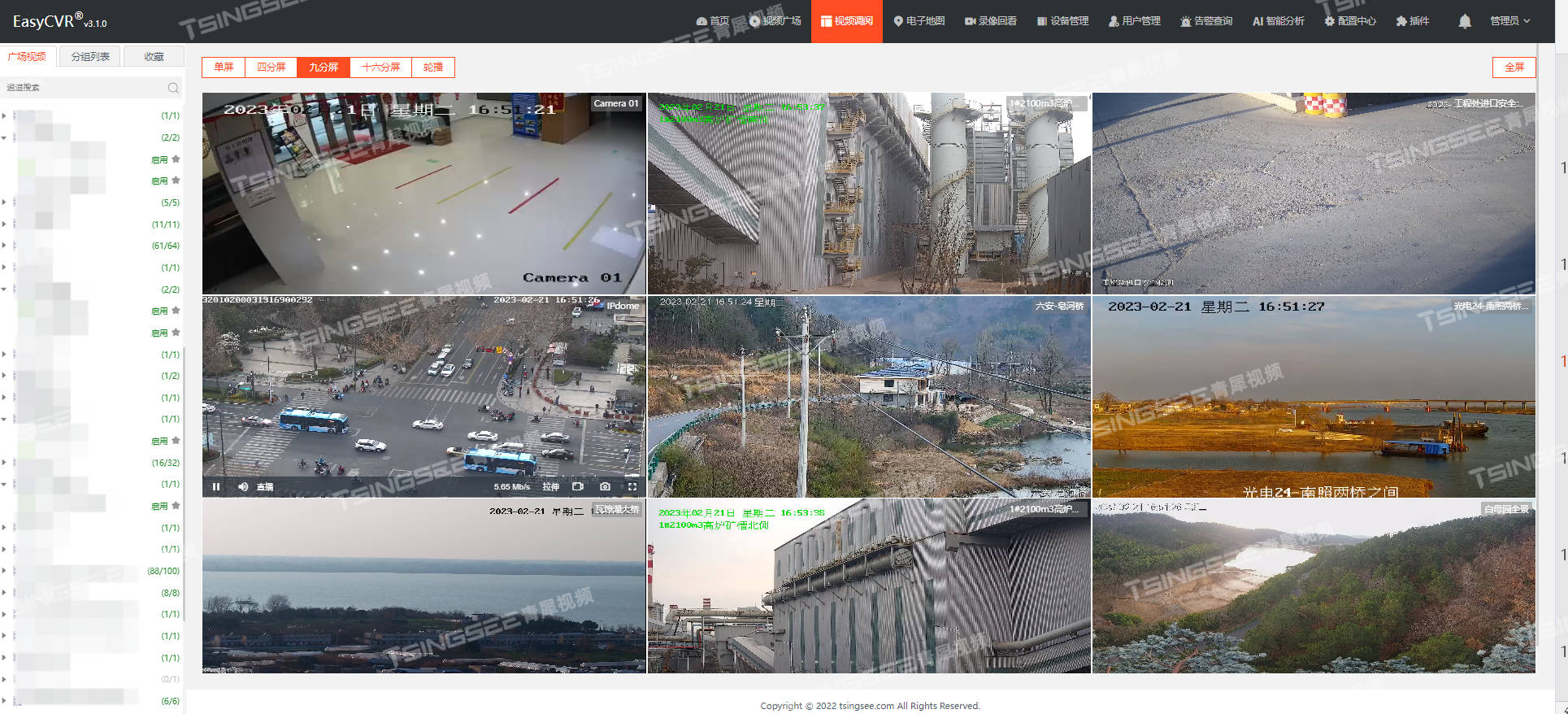
安防监控/视频汇聚平台EasyCVR调用rtsp地址返回的IP不正确是什么原因?
安防监控/云存储/磁盘阵列存储/视频汇聚平台EasyCVR可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有GB28181、RTSP/Onvif、RTMP等,以及厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等,能对外分发RTSP、RT…...

媒体服务器与视频服务器有什么区别
媒体服务器与视频服务器有什么区别 流媒体服务器用在远程教育,视频点播、网络电台、网络视频等方面。 直播过程中就需要使用流媒体服务器,一个完整的直播过程,包括采集、处理、编码、封包、推流、传输、转码、分发、解码、播放等过程…...
:循环语句)
菜鸟教程《Python 3 教程》笔记(11):循环语句
菜鸟教程《Python 3 教程》笔记(11) 11 循环语句11.1 while 循环11.1.1 while 循环使用 else 语句 11.2 for 语句11.2.1 for...else 11.3 break 和 continue 语句及循环中的 else 子句 11 循环语句 出处: 菜鸟教程 - Python3 循环语句 11.1…...
【DevOps视频笔记】8. Jenkins 配置
一、Jenkins 入门配置 1. 工具 / 插件 介绍 二、插件和工具配置 1. 配置 JDK 和 Maven Stage 1:将服务器中 JDK 和 Maven 映射到 jenkins 容器中 Stage 2:jenkins 全局配置中 -- 指定JAVA_HOME目录 Stage 3:jenkins 全局配置中 -- 指定…...

C# 在Color[] colorTable中快速找到Color的索引位置
C# 在Color[] colorTable中快速找到Color的索引位置 第一种方法: 如果您需要在Color[] colorTable中快速查找特定Color的索引位置,可以使用C#的Array.FindIndex方法。这个方法接受一个回调函数作为参数,该函数定义了如何判断数组元素是否与…...

go学习笔记 炒土豆丝
今天的主菜是土豆,就来个土豆丝吧。我的大致流程如下: 1.挑选白瓤土豆,洗它 2.土豆去皮 3.土豆切片,切丝,丝要粗细均匀 4.清洗几遍土豆丝,去除上面的淀粉,在清水中泡一小会 5.起锅,放…...

FPGA VR摄像机-拍摄和拼接立体 360 度视频
本文介绍的是 FPGA VR 相机的第二个版本,第一个版本是下面这样: 第一版地址: ❝ https://hackaday.io/project/26974-vr-camera-fpga-stereoscopic-3d-360-camera ❞ 本文主要介绍第二版本,第二版本的 VR 摄像机,能够以…...
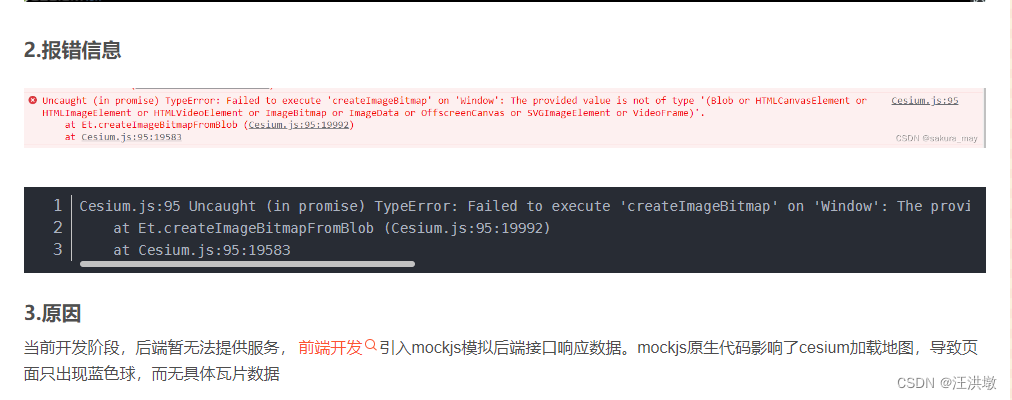
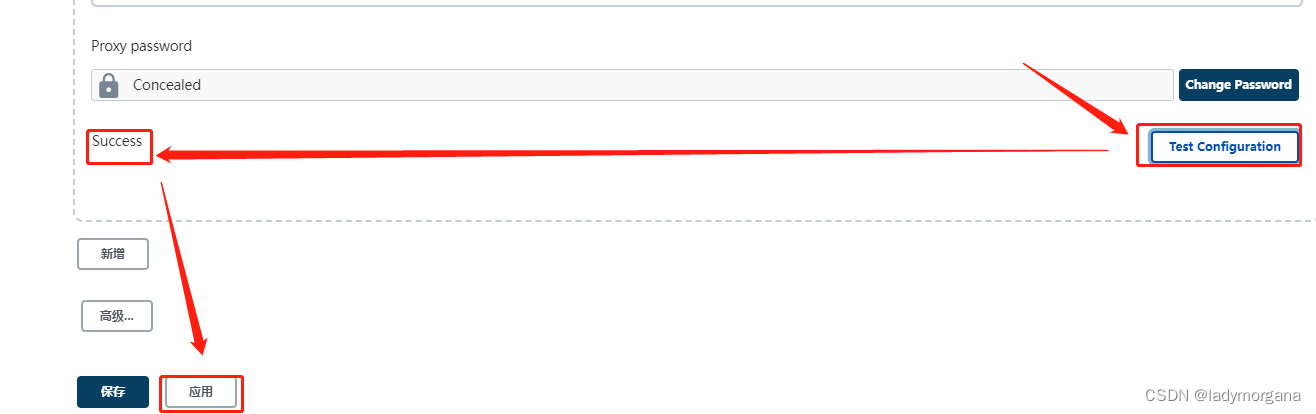
vue集成mars3d后,basemaps加不上去
首先: <template> <div id"centerDiv" class"mapcontainer"> <mars-map :url"configUrl" οnlοad"onMapload" /> </div> </template> <script> import MarsMap from ../component…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...
