范德波尔方程详细介绍与Python实现(附说明)
引言:
在研究真空管放大器的过程中,写下了一个振动微分方程。当时人们并没有混沌或是对初始条件敏感的概念。不过,当混沌理论有一定发展后,人们重新回顾这个方程时发现它其实是个混沌方程。当时,范德波尔在 Nature 杂志报告了基于这个微分方程的霓虹灯实验,发现当驱动信号具有某种自然频率时,会听到毫无规律的“噪音”。然而方程如下所示,其中并没有随机噪声项:
他当时不明白这种无规律的振荡从何而来,后来才被搞清楚是混沌波动。多年之后,英国数学家玛丽·卡特赖特和李特尔伍德继续研究范德波尔电路。他们发现参数的不适当选择会导致方程解的不稳定性,而且变得不可预测。这就是后来弄明白了的所谓的“蝴蝶效应”。
范德波尔方程详细介绍与Python实现(附说明)
- 1. 范德波尔方程
- 1.1 范德波尔方程形式
- 1.2 范德波尔方程的作用
- 2. Python测试
- 2.1 测试函数说明
- 2.2 代码实现
1. 范德波尔方程
1.1 范德波尔方程形式
范德波尔方程是单自由度线性振动系统附加非线性阻尼项的动力学方程。是最基本的自激振动方程,为典型的振动方程之一,又称为范德波尔振子或范德波尔系统。
相关文章:
)
范德波尔方程详细介绍与Python实现(附说明)
引言: 在研究真空管放大器的过程中,写下了一个振动微分方程。当时人们并没有混沌或是对初始条件敏感的概念。不过,当混沌理论有一定发展后,人们重新回顾这个方程时发现它其实是个混沌方程。当时,范德波尔在 Nature 杂志报告了基于这个微分方程的霓虹灯实验,发现当驱动信号…...
常用的GPT插件
0.简介 随着chatgpt爆火,这玩意并不对国内用户开放,如果想要使用的话还要需要进行翻墙以及国外手机号才能进行注册。 对于国内来说有很多国内免费的方法,这里就整理一下,方便大家开发 1. 网站类型 下面的网站无需注册即可免费…...

智慧校园用电安全解决方案
随着科技的不断发展,智慧校园建设逐渐成为了教育行业的一大趋势。在这个过程中,电力系统作为校园基础设施的重要组成部分,其安全、稳定、高效的运行显得尤为重要。下面小编来为大家介绍下智慧校园用电安全解决方案吧! 一、智慧校园电力系统现…...
【教程】DGL中的子图分区函数partition_graph讲解
转载请注明出处:小锋学长生活大爆炸[xfxuezhang.cn] 目录 函数形式 函数作用 函数内容 函数入参 函数返参 使用示例 实际上官方的函数解释中就已经非常详细了。 函数形式 def partition_graph(g, graph_name, num_parts, out_path, num_hops1, part…...

关于layui table回显以及选择下一页时记住上一页数据的问题
代码如下 <div class"layui-form-item"><label class"layui-form-label">选择商品</label><div class"layui-input-inline"><input type"text" name"keyword" id"keyword" placehold…...
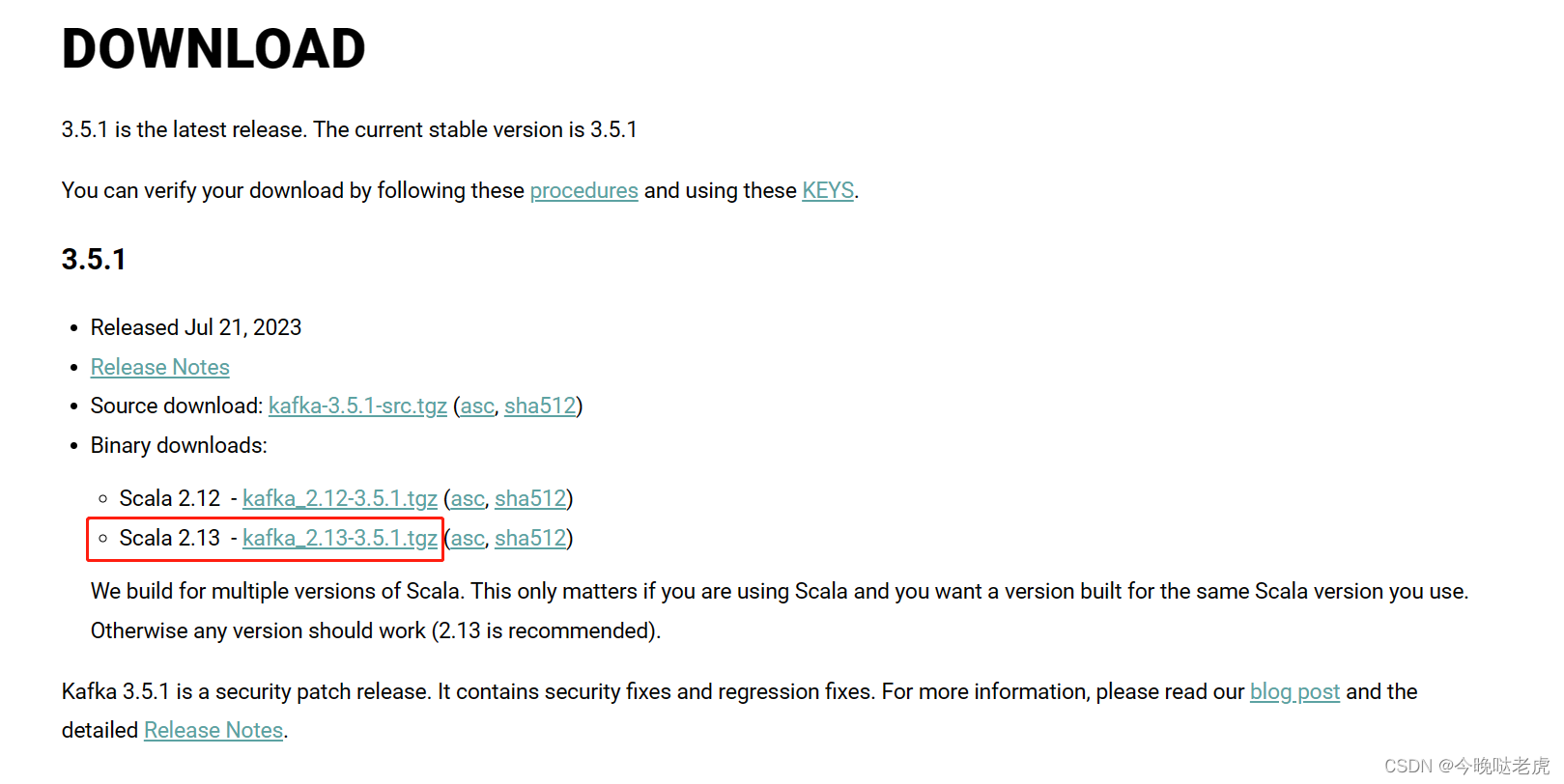
kafka消息系统实战
kafka是什么? 是一种高吞吐量的、分布式、发布、订阅、消息系统 1.导入maven坐标 <dependency><groupId>org.apache.kafka</groupId><artifactId>kafka-clients</artifactId><version>2.4.1</version></dependency&…...

Kafka3.0.0版本——Leader故障处理细节原理
目录 一、服务器信息二、服务器基本信息及相关概念2.1、服务器基本信息2.2、LEO的概念2.3、HW的概念 三、Leader故障处理细节 一、服务器信息 三台服务器 原始服务器名称原始服务器ip节点centos7虚拟机1192.168.136.27broker0centos7虚拟机2192.168.136.28broker1centos7虚拟机…...
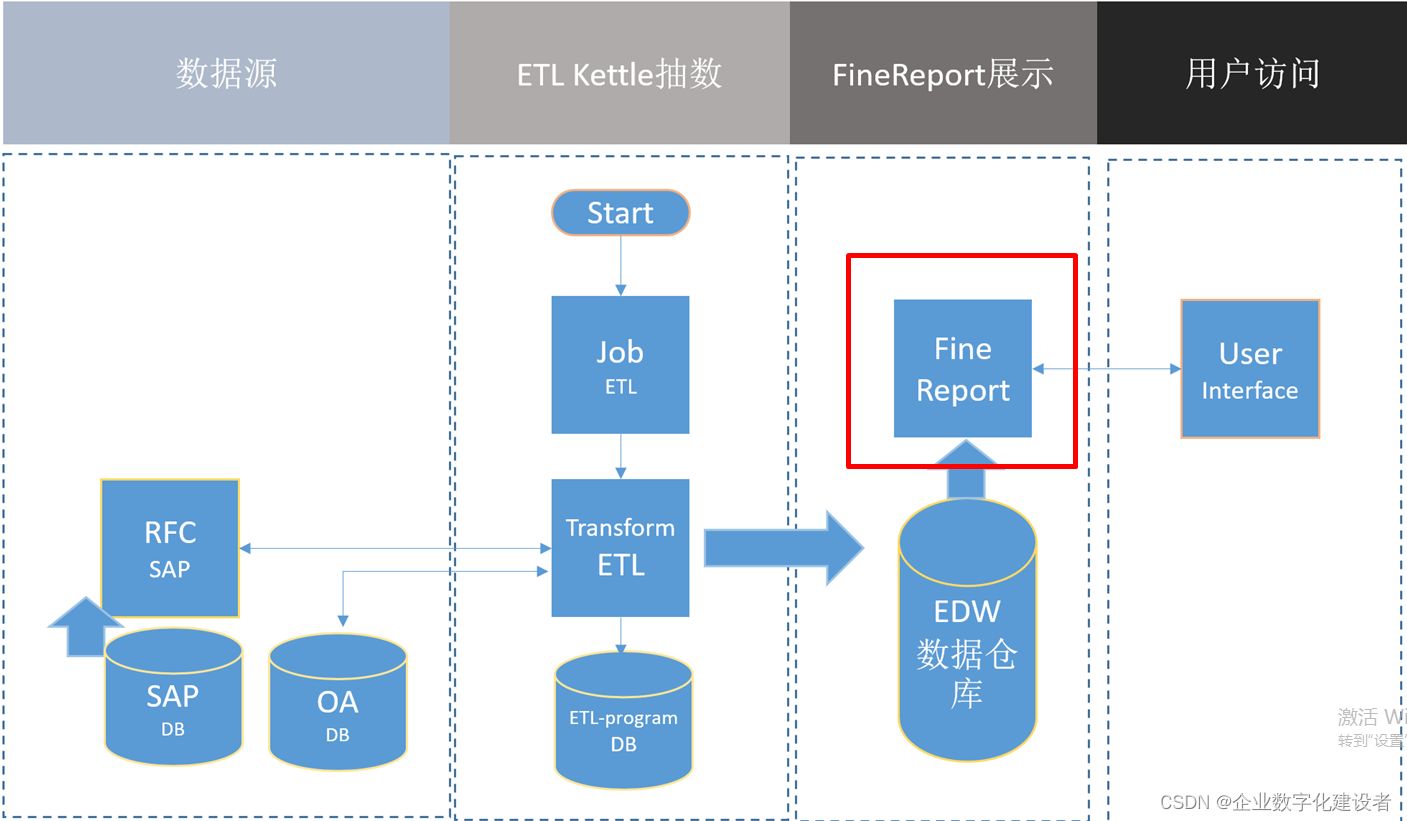
BI系统框架模型
一 技术架构 二 数据源 主数据 :组织|岗位|人员|大区|三大主数据(客户、物料、供应商)财务主数据(科目|成本中心|利润中心|资产)|工作中心|工艺路线 业务数据 :线索|业务机会|合同|订单|采购|生产|发…...
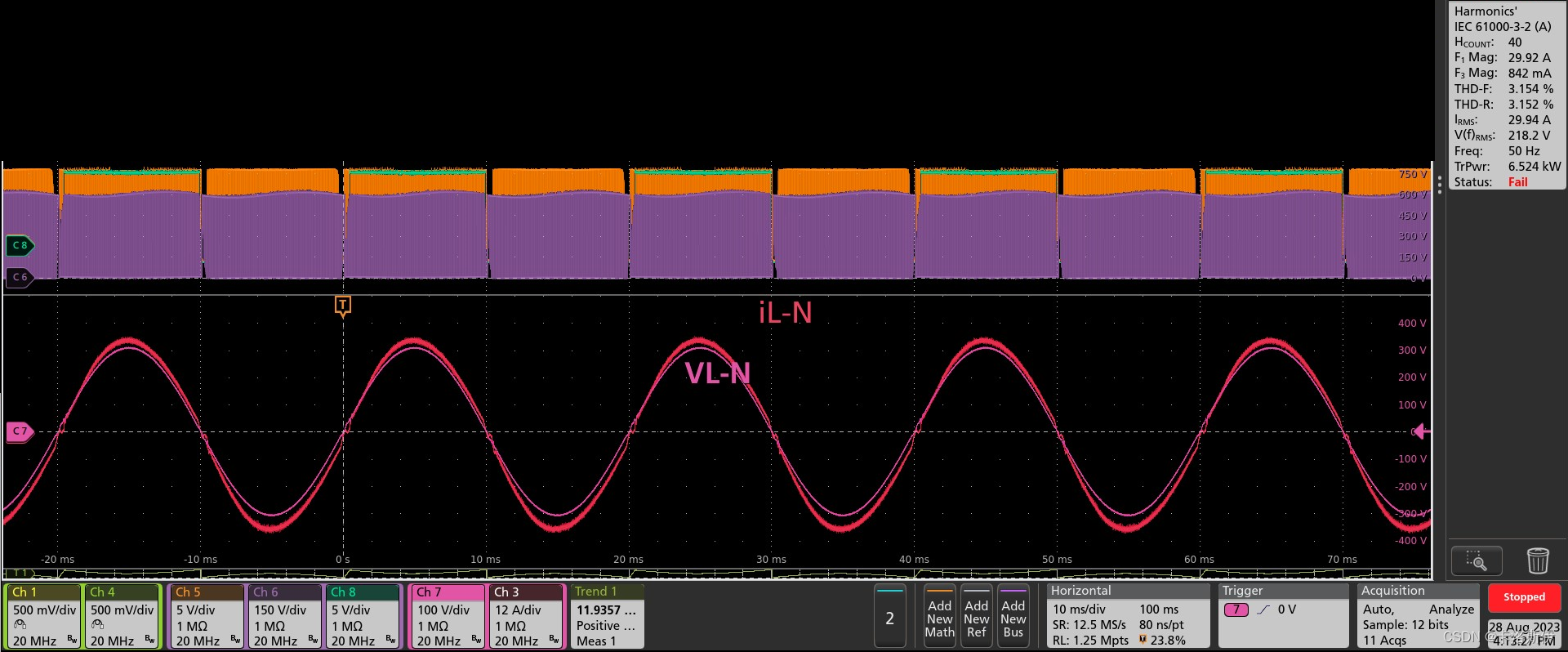
双向交错CCM图腾柱无桥单相PFC学习仿真与实现(3)硬件功能实现
前言 前面介绍了双向交错CCM图腾柱的系统设计仿真实现,仿真很理想 双向交错CCM图腾柱无桥单相PFC学习仿真与实现(1)系统问题分解_卡洛斯伊的博客-CSDN博客 然后又介绍了SOG锁相环仿真实现的原理 双向交错CCM图腾柱无桥单相PFC学习仿真与实…...

微软用 18 万行 Rust 重写了 Windows 内核
微软正在使用 Rust 编程语言重写其核心 Windows 库。 5 月 11 日——Azure 首席技术官 Mark Russinovich 表示,最新的 Windows 11 Insider Preview 版本是第一个包含内存安全编程语言 Rust 的版本。 “如果你参加了 Win11 Insider 环,你将在 Windows 内…...
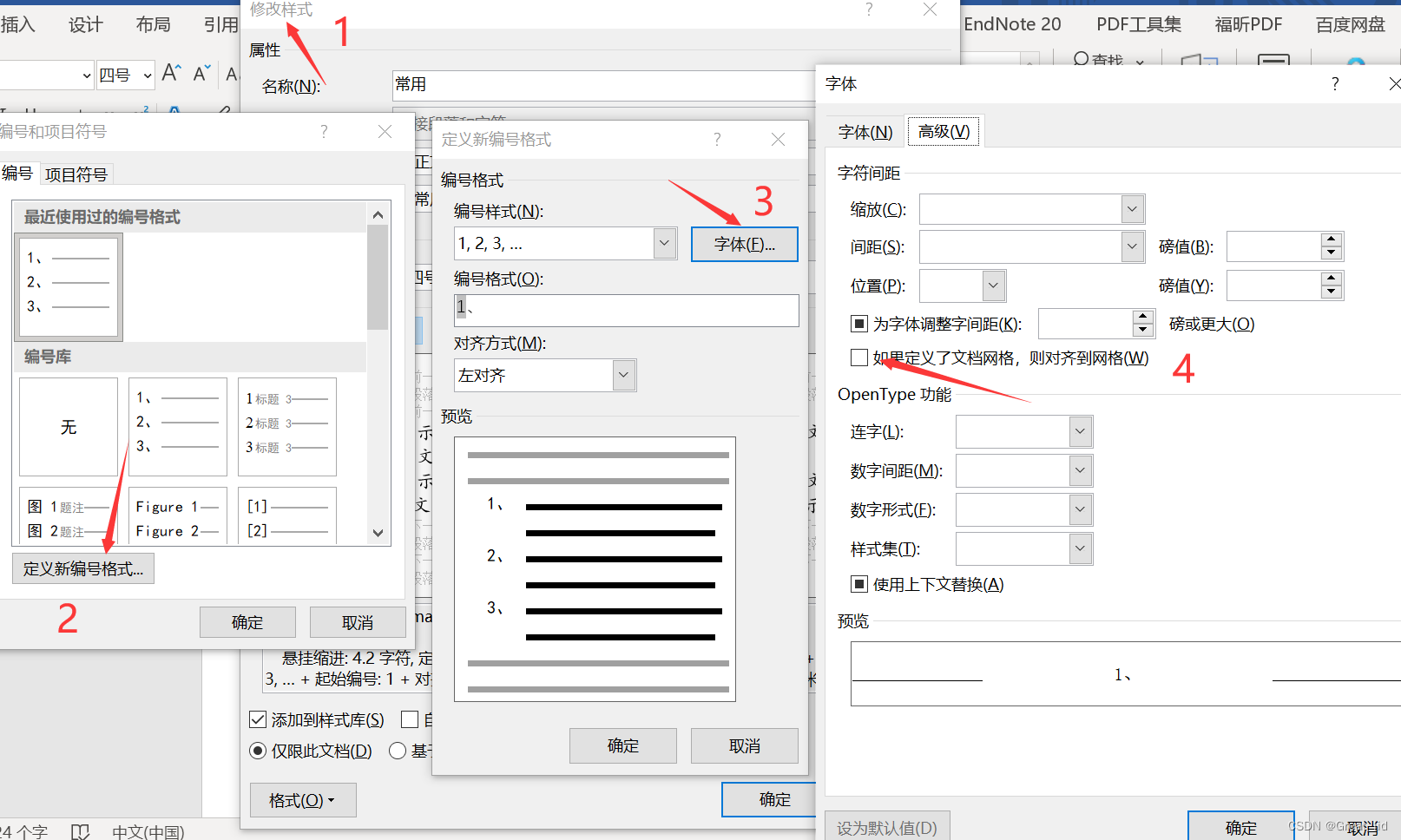
word 调整列表缩进
word 调整列表缩进的一种方法,在试了其他方法无效后,按下图所示顺序处理,编号和文字之间的空白就没那么大了。 即右键word上方样式->点击修改格式->定义新编号格式->字体->取消勾选 “……对齐到网格”->确定...

nginx学习
一、nginx常用版本 Nginx开源版: http://nginx.org/ nginx plus商业版本(好像功能支持更多) https://www.nginx.com/ openresty (免费,用的也是这个) https://openresty.org/cn/ Tengine https://tengine.…...
python+TensorFlow实现人脸识别智能小程序的项目(包含TensorFlow版本与Pytorch版本)(一)
pythonTensorFlow实现人脸识别智能小程序的项目(包含TensorFlow版本与Pytorch版本)(一) 一:TensorFlow基础知识内容部分(简明扼要,快速适应)1、下载Cifar10数据集,并进行…...

ChatGPT怎么用于政府和公共服务?
将ChatGPT用于政府和公共服务领域是一种创新的应用方式,可以改善政府与公众之间的互动,提升公共服务的效率和质量。ChatGPT作为一个自然语言处理模型,可以在政府信息传递、公共参与、服务支持等方面发挥积极作用。以下将详细探讨ChatGPT如何用…...
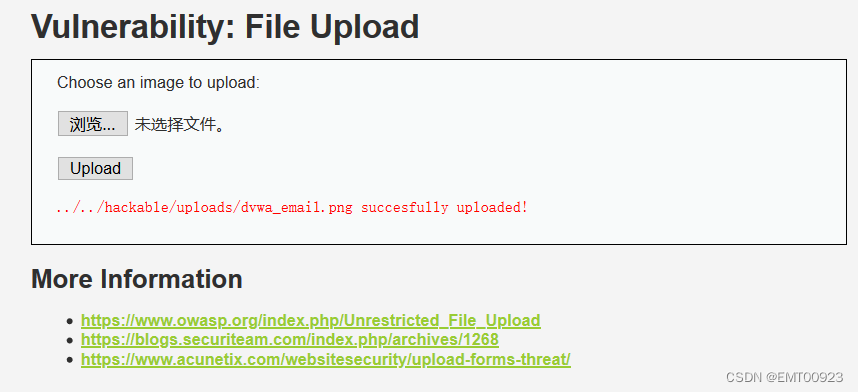
dvwa文件上传通关及代码分析
文章目录 low等级medium等级high等级Impossible等级 low等级 查看源码: <?phpif( isset( $_POST[ Upload ] ) ) {// Where are we going to be writing to?$target_path DVWA_WEB_PAGE_TO_ROOT . "hackable/uploads/";$target_path . basename( …...
数字孪生:重塑政府决策与公共服务
在之前的文章中为大家分享了数字孪生在很多行业的应用场景,本文和大家一起探讨一下数字孪生在政务管理方面能有哪些应用,以及其对公共服务提供的积极影响。 1)城市规划方面 数字孪生技术可用于模拟城市的发展和规划。政府可以建立城市的虚拟…...

Leetcode:【448. 找到所有数组中消失的数字】题解
题目 给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。 难度:简单 题目链接:448. 找到所有数组中消失的数字 示例1 输入&…...

2023年中,量子计算产业现状——
2023年上半年,量子计算(QC)领域取得了一系列重要进展和突破,显示出量子计算技术的快速发展和商业应用的不断拓展。在iCV TAnk近期发表的一篇报告中,团队从制度进步、产业生态、投融资形势、总结与展望四个方面对量子计…...

微信小程序智慧流调微信小程序设计与实现
摘 要 自从2020年新冠疫情爆发以来,对全国人民的健康和全国各地区的经济发展都带来了很大的影响,并且新冠肺炎对各个领域带来的影响还未完全消除。近三年以来,全国各地区多次爆发新的疫情,导致许多人被隔离,也导致全国…...

分布式集群框架——有关zookeeper的面试考点
3.掌握Zookeeper的概念 当涉及到大规模分布式系统的协调和管理时,Zookeeper是一个非常重要的工具。 1. 分布式协调服务:Zookeeper是一个分布式协调服务,它提供了一个高可用和高性能的环境,用于协调和同步分布式系统中的各个节点…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...
