当前位置： 首页 > news >正文

Facebook message tag 使用攻略

news 2025/9/16 0:11:07

e427678f5274f34dfa85a7805b471b96.jpeg

Messenger 讯息传不出去？无法发送FB 讯息给非好友？ 2020年3月，Facebook 为了防止用户被过多的推广或垃圾讯息困扰而更新使用条款，现在商家要用FB传讯息给所有人（包括非好友），应该使用 Facebook Message Tag，以免被封锁导致 FB messenger 无法传送讯息。

Facebook message tag 是什么？

简单而言，message tag 是Facebook 讯息的标签，用途是让商家在一般的24小时对话限制外（24小时由顾客开启对话开始倒数），发送重要资讯或1:1更新给顾客。同时，Facebook官方会透过标签，得知讯息类型。

换言之，message tag 不能用作推广用途。商家不可以在讯息上加上推广、优惠、折扣等相关标签。


那facebook message tag 到底又什么好处？其实 Message tag 是和顾客互动的工具，以下是建议使用message tag 的好时机。

message tag 更新活动资讯 

  • 确认预约或活动出席
  • 提醒顾客即将来临的活动
  • 通知顾客活动的最新安排

message tag 更新售后资讯

  • 发送收据
  • 更新付款详情
  • 更新物流详情
  • 通知紧急订单变动，如付款失败、延迟寄货


5个 Facebook Message Tag 信息避雷

请切记不要滥用 message tag 来发送以下内容，以避免 FB messenger 无法传送讯息：

  • 推广内容（优惠、折扣）
  • 已经发生的活动回顾
  • 顾客未有报名参与的活动资讯
  • 问卷、评价、投票邀请
  • 推荐更高单价或其他类型的产品（cross-selling/upselling）


Facebook 专页发讯息的方法

Facebook 专页发讯息有24小时限制——只有在顾客回应商家后的24小时内，可以传送讯息给对方。那要怎么主动出击，让顾客找上你聊天呢？这边推荐使用 Click-to-Messenger Ads，对方一点击广告就会被带到 Messenger，精准找到目标客户。不过每当客户越来越多，我们就不得不使用其他工具来帮我们管理客户，我推荐的是SaleSmartly，一款全渠道集成聊天管理工具。

bcdc3bcdfd29c6a5b89fb1608eca70a8.jpeg

您所有的多渠道消息，集中在一个地方，通过在线聊天（Livechat）、Messenger、 WhatsApp、Telegram、 Instagram、Line、Emai、WeChatl等无缝销售、营销或服务，以获得统一的客户体验。

相关文章：

Facebook message tag 使用攻略

Messenger 讯息传不出去？无法发送FB 讯息给非好友？ 2020年3月，Facebook 为了防止用户被过多的推广或垃圾讯息困扰而更新使用条款，现在商家要用FB传讯息给所有人（包括非好友），应该使用 Facebook …...

编程日记 2023/8/30 11:58:43

气传导耳机哪个品牌比较好？综合表现很不错的气传导耳机推荐

​气传导耳机不仅能够提升幸福感还能听到周围环境声，大大提高安全性。如果你在寻找一款高品质的气传导耳机，又不知从何入手时，不要担心，我已经为你精心挑选了四款市面上综合表现很不错的气传导耳机，让你享受更好的音质…...

编程日记 2023/8/30 11:57:42

Rabbitmq的消息转换器

Spring会把你发送的消息序列化为字节发送给MQ，接收消息的时候，还会把字节反序列化为Java对象 ,只不过，默认情况下Spring采用的序列化方式是JDK序列化。众所周知，JDK序列化存在下列问题： 数据体积过大 有安全漏洞 可读…...

编程日记 2023/8/30 11:56:40

nvidia-docker的使用

拉取镜像 docker pull nvidia/cuda可能出现的问题 问题描述 Error response from daemon: manifest for nvidia/cuda:latest not found: manifest unknown: manifest解决方法： 为找到正确且合适的docker镜像版本 在supported-tags中找到与自己系统对应的cuda版本…...

编程日记 2023/8/30 11:55:38

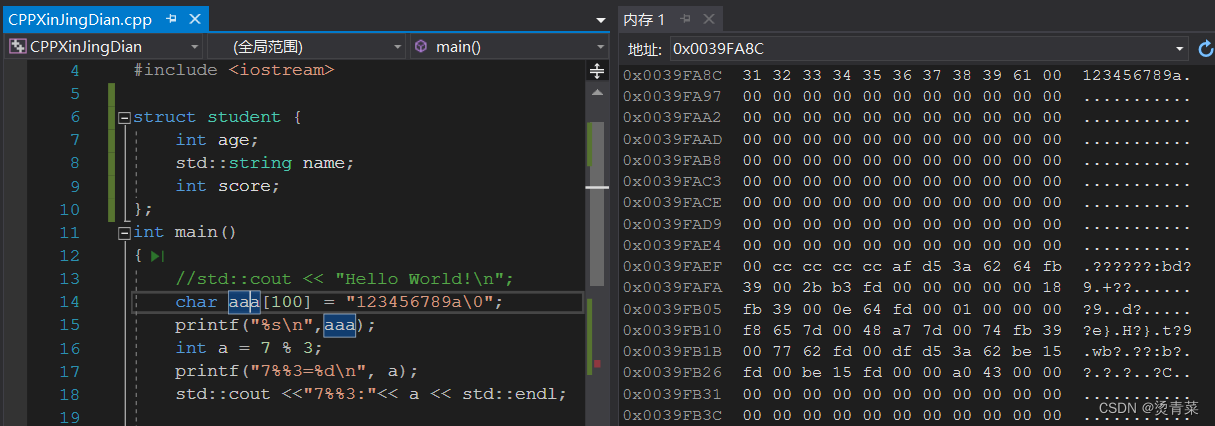
C++新经典 | C语言

目录 一、基础之查漏补缺 1.float精度问题 2.字符型数据 3.变量初值问题 4.赋值&初始化 5.头文件之<> VS " " 6.逻辑运算 7.数组 7.1 二维数组初始化 7.2 字符数组 8.字符串处理函数 8.1 strcat 8.2 strcpy 8.3 strcmp 8.4 strlen 9.函数 …...

编程日记 2023/8/30 11:54:37

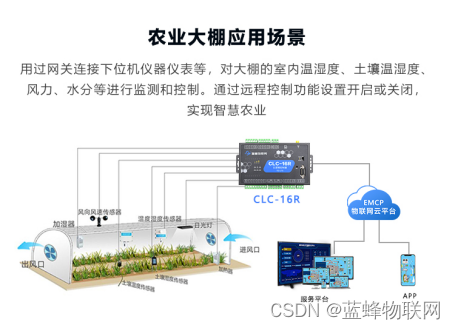
物联网智慧种植农业大棚系统

一、项目背景 智慧农业是是将物联网技术和农业生产箱管理的新型农业&#xff0c;依托部署在农业生产现场的各种传感节点&#xff0c;以物联网网关为通道形成数据传输网络&#xff0c;可以实现控制柜、环境监测传感器、气象监测机器等设备的远程监控&#xff0c;达到及时高校的…...

编程日记 2023/8/30 11:53:34

TabBar组件如何跳转页面？

1、先引入 2、假数据 const tabs [{key: home,title: 首页,icon: <AppOutline />,badge: Badge.dot,},{key: todo,title: 待办,icon: <UnorderedListOutline />,badge: 5,},{key: message,title: 消息,icon: (active: boolean) >active ? <MessageFill /&…...

编程日记 2023/8/30 11:52:33

Vue.js中，router和route

<div class"search">{{$route.params.things}}<van-nav-bar fixed title"商品列表" left-arrow click-left"$router.go(-1)" /><van-searchreadonlyshape"round"background"#ffffff"value"手机"sh…...

编程日记 2023/8/30 11:51:32

【微服务】07-缓存

文章目录 为不同的场景设计合适的缓存策略1. 缓存是什么2. 缓存的场景3. 缓存的策略4. 缓存位置5. 缓存实现的要点6. 注意问题7. 使用的组件8. 内存缓存和分布式缓存区别 总结 为不同的场景设计合适的缓存策略 1. 缓存是什么 缓存是计算结果的“临时”存储和重复使用缓存本质…...

编程日记 2023/8/30 11:50:30

权限校验中的“双token”方案

1. 双Token中的两个token分别是什么&#xff1f; 1.1 access_token 1.2 fresh_token 2. 为什么需要双token&#xff1f;一个token不行吗&#xff1f; 答&#xff1a; 两个token的职责不同。其中&#xff0c;access_token是在每次请求的时候携带给后端进行权限校验&#xff…...

编程日记 2023/8/30 11:49:28

TensorFlow的基本概念

TensorFlow 是由 Google 开发的开源机器学习框架&#xff0c;其基本概念如下&#xff1a; 1. 张量&#xff08;Tensor&#xff09;&#xff1a;TensorFlow 中最基本的数据结构&#xff0c;是多维数组&#xff0c;可以理解为向量或矩阵的推广。常见的张量有常量张量、变量张量和…...

编程日记 2023/8/30 11:48:25

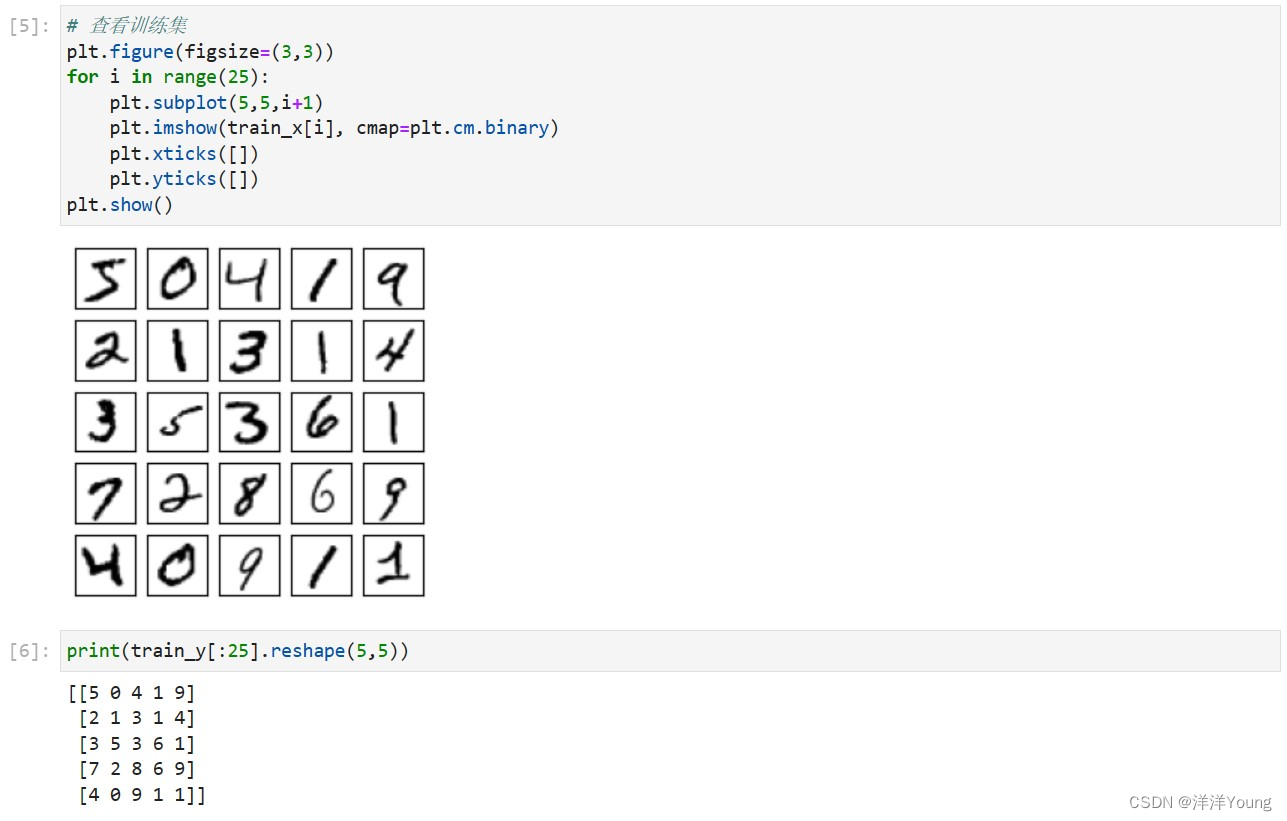
【卷积神经网络】MNIST 手写体识别

LeNet-5 是经典卷积神经网络之一&#xff0c;1998 年由 Yann LeCun 等人在论文 《Gradient-Based Learning Applied to Document Recognition》中提出。LeNet-5 网络使用了卷积层、池化层和全连接层&#xff0c;实现可以应用于手写体识别的卷积神经网络。TensorFlow 内置了 MNI…...

编程日记 2023/8/30 11:47:24

Ansible学习笔记2

Ansible是Python开发的自动化运维工具&#xff0c;集合了众多运维工具&#xff08;Puppet、cfengine、chef、func、fabric&#xff09;的优点&#xff0c;实现了批量系统配置&#xff0c;批量程序部署、批量运行命令等功能。 特点&#xff1a; 1&#xff09;部署简单&#xff…...

编程日记 2023/8/30 11:46:23

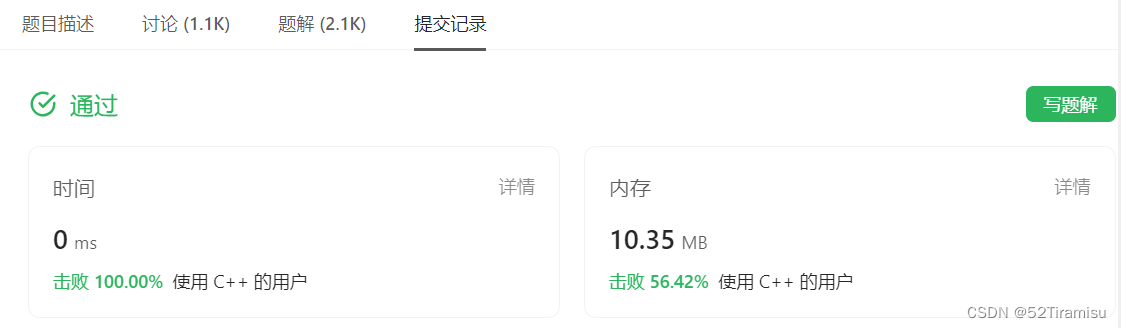
80. 删除有序数组中的重复项 II

【中等题】 题目&#xff1a; 给你一个有序数组 nums &#xff0c;请你 原地 删除重复出现的元素&#xff0c;使得出现次数超过两次的元素只出现两次 &#xff0c;返回删除后数组的新长度。 不要使用额外的数组空间&#xff0c;你必须在 原地 修改输入数组 并在使用 O(1) 额…...

编程日记 2023/8/30 11:45:21

CVE-2023-36874 Windows错误报告服务本地权限提升漏洞分析

CVE-2023-36874 Windows错误报告服务本地权限提升漏洞分析 漏洞简介 Windows错误报告服务在提交错误报告前会创建wermgr.exe进程&#xff0c;而攻击者使用特殊手法欺骗系统创建伪造的wermgr.exe进程&#xff0c;从而以system权限执行代码。 影响版本 Windows10 1507 * Wind…...

编程日记 2023/8/30 11:44:20

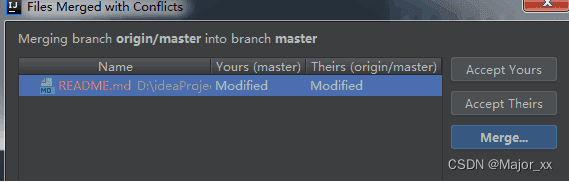
IDEA遇到 git pull 冲突的几种解决方法

1 忽略本地修改&#xff0c;强制拉取远程到本地 主要是项目中的文档目录&#xff0c;看的时候可能多了些标注&#xff0c;现在远程文档更新&#xff0c;本地的版本已无用&#xff0c;可以强拉 git fetch --all git reset --hard origin/dev git pull关于commit和pull的先后顺…...

编程日记 2023/8/30 11:43:19

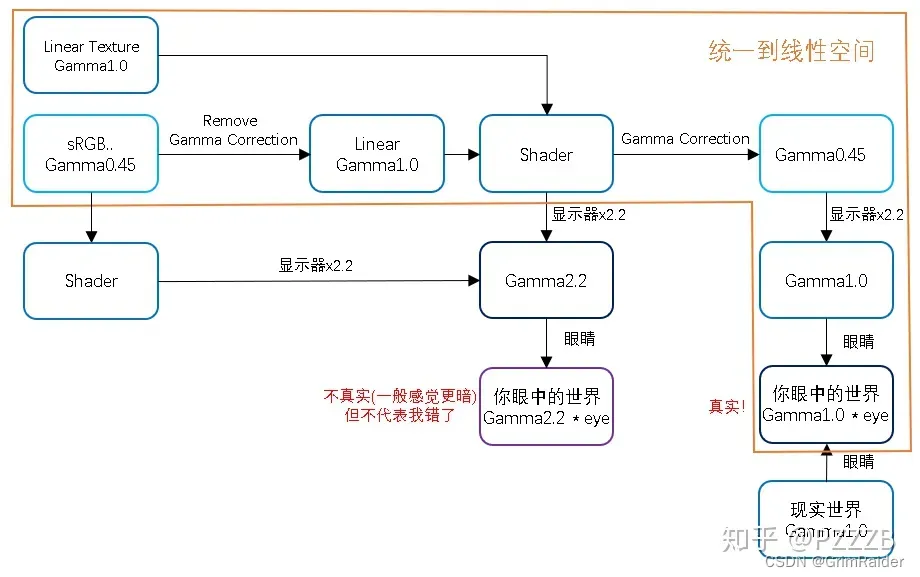
[Unity]UI和美术出图效果不一致

问题描述&#xff1a;美术使用PS在Gamma空间下设计的UI图&#xff0c;导入到Unity&#xff0c;因为Unity使用的是线性空间&#xff0c;导致半透明的UI效果和美术设计的不一致。 解决方案&#xff1a; &#xff08;一&#xff09;让美术在线性空间下工作 &#xff08;二&…...

编程日记 2023/8/30 11:42:18

SpringBoot整合JPA和Hibernate框架

Springboot整合JPAHibernate框架【待完成】 随着MybatisPlus技术的发展&#xff0c;JPA和Hibernate技术已经逐步淘汰 JPA遵循了Hibernate框架规则&#xff0c;目前使用的不多 1、添加依赖 <!--jpa--> <dependency><groupId>org.springframework.boot</…...

编程日记 2023/8/30 11:41:16

Java中文件的创建(三种方式)，文件常用的方法

文件的创建 方式1&#xff1a; new File(String pathName) 根据路径构建一个File对象方式2&#xff1a; new File(File parent,String child) 根据父目录文件子路径构建方式3&#xff1a; new File(String parent,String child) 根据父目录子路径构建 代码&#xff1a; //方…...

编程日记 2023/8/30 11:40:15

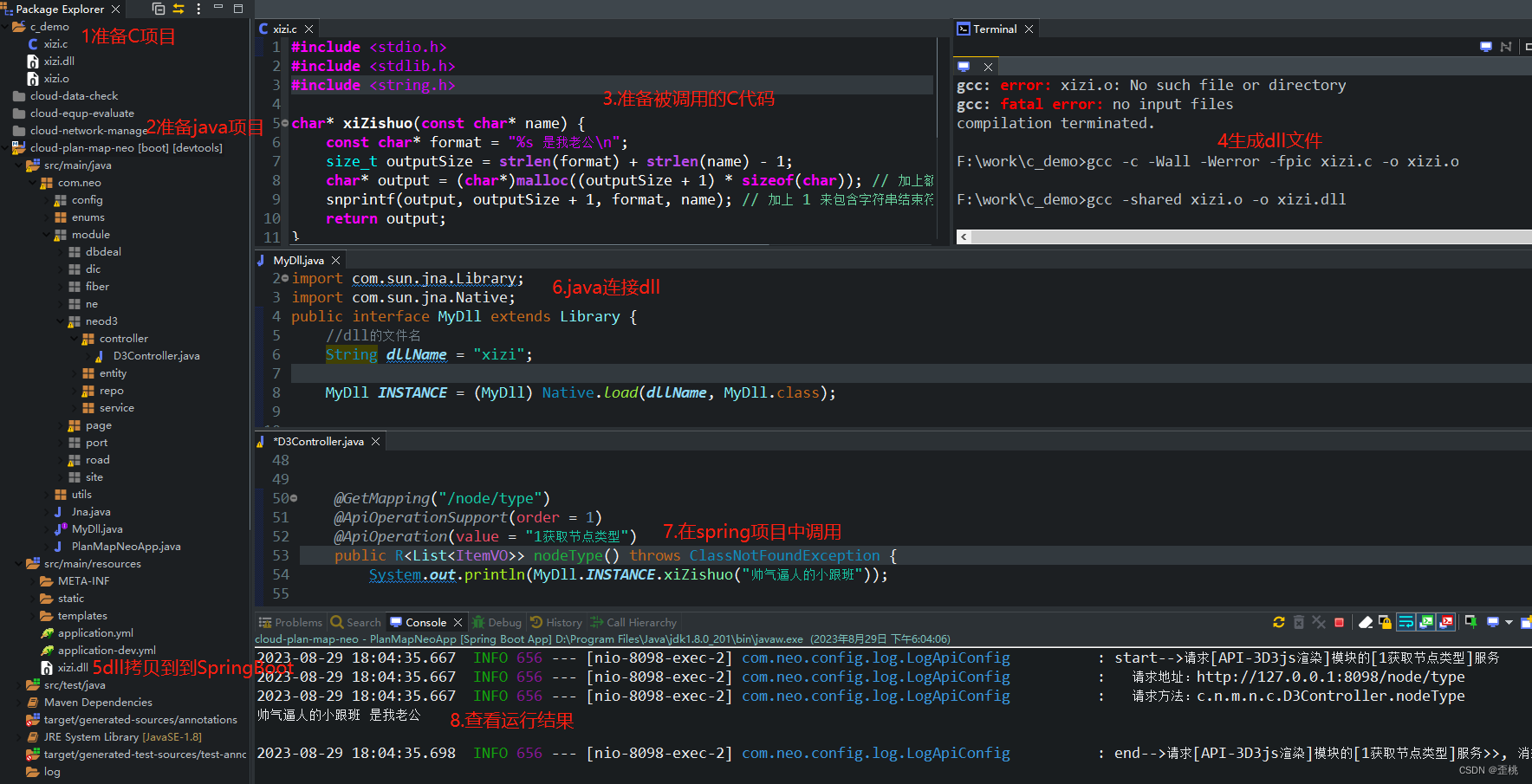
Spring boot中调用C/C++（dll）

添加JNA依赖 <dependency><groupId>net.java.dev.jna</groupId><artifactId>jna</artifactId><version>5.5.0</version> </dependency>准备C代码/C代码 如下是C代码&#xff0c;文件名&#xff1a;xizi.c #include <std…...

编程日记 2023/8/30 11:39:14

pam_env.so模块配置解析

在PAM&#xff08;Pluggable Authentication Modules&#xff09;配置中&#xff0c; /etc/pam.d/su 文件相关配置含义如下&#xff1a; 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块&#xff0c;负责验证用户身份&am…...

编程新知 2025/8/21 21:33:01

《用户共鸣指数（E）驱动品牌大模型种草：如何抢占大模型搜索结果情感高地》

在注意力分散、内容高度同质化的时代&#xff0c;情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现&#xff0c;消费者对内容的“有感”程度&#xff0c;正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中&#xff0…...

编程新知 2025/9/14 12:35:12

Unit 1 深度强化学习简介

Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库&#xff0c;例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体&#xff0c;比如 SnowballFight、Huggy the Do…...

编程新知 2025/7/31 23:29:01

MySQL中【正则表达式】用法

MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现&#xff08;两者等价&#xff09;&#xff0c;用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例&#xff1a; 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

编程新知 2025/9/13 11:37:54

ios苹果系统，js 滑动屏幕、锚定无效

现象&#xff1a;window.addEventListener监听touch无效&#xff0c;划不动屏幕&#xff0c;但是代码逻辑都有执行到。 scrollIntoView也无效。 原因&#xff1a;这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作&#xff0c;从而会影响…...

编程新知 2025/9/12 23:22:17

docker 部署发现spring.profiles.active 问题

报错&#xff1a; org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

编程新知 2025/9/8 9:55:21

Pinocchio 库详解及其在足式机器人上的应用

Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库&#xff0c;专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性&#xff0c;并提供了一个通用的框架&…...

编程新知 2025/8/27 0:04:53

AGain DB和倍数增益的关系

我在设置一款索尼CMOS芯片时&#xff0c;Again增益0db变化为6DB&#xff0c;画面的变化只有2倍DN的增益&#xff0c;比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析&#xff1a; 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

编程新知 2025/7/8 0:38:36

力扣热题100 k个一组反转链表题解

题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

编程新知 2025/9/14 8:32:04

​​企业大模型服务合规指南：深度解析备案与登记制度​​

伴随AI技术的爆炸式发展&#xff0c;尤其是大模型&#xff08;LLM&#xff09;在各行各业的深度应用和整合&#xff0c;企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者&#xff0c;还是积极拥抱AI转型的传统企业&#xff0c;在面向公众…...

编程新知 2025/9/15 5:17:28