【卷积神经网络】MNIST 手写体识别
LeNet-5 是经典卷积神经网络之一,1998 年由 Yann LeCun 等人在论文 《Gradient-Based Learning Applied to Document Recognition》中提出。LeNet-5 网络使用了卷积层、池化层和全连接层,实现可以应用于手写体识别的卷积神经网络。TensorFlow 内置了 MNIST 手写体数据集,可以很方便地读取数据集,并应用于后续的模型训练过程中。本文主要记录了如何使用 TensorFlow 2.0 实现 MNIST 手写体识别模型。
目录
1 数据集准备
2 模型建立
3 模型训练
1 数据集准备
TensorFlow 内置了 MNIST 手写体数据集,安装 TensorFlow 之后,使用如下代码就可以加载 MNIST 数据集:
import tensorflow as tfmnist = tf.keras.datasets.mnist
(train_x, train_y), (test_x, test_y) = mnist.load_data()使用 Matplotlib 查看前 25 张图片,并打印对应的标签。
from matplotlib import pyplot as plt# 查看训练集
plt.figure(figsize=(3,3))
for i in range(25):plt.subplot(5,5,i+1)plt.imshow(train_x[i], cmap=plt.cm.binary)plt.xticks([])plt.yticks([])
plt.show()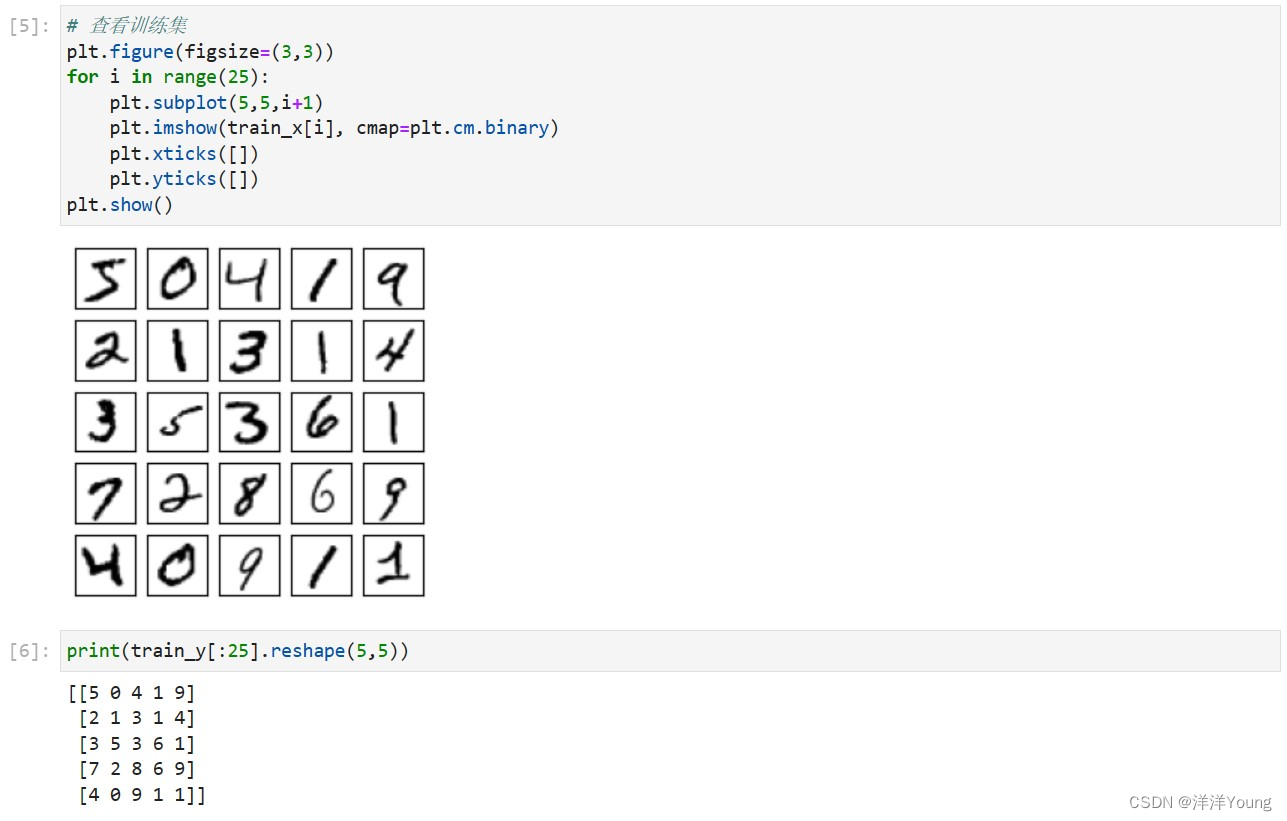
接着,使用 tf.one_hot() 函数,对图像的标签进行独热码编码。
# 预处理
train_y = tf.one_hot(train_y, depth=10)
test_y = tf.one_hot(test_y, depth=10)2 模型建立
MNIST 手写体数据集中,每张图像的大小是 28 × 28 × 1,按照 LeNet-5 模型的思路,构建卷积神经网络模型。选择 5 × 5 的卷积核,卷积层之后是 2 × 2 的平均池化,激活函数选择 sigmoid(除了最后一层)。
# the first layer can receive an 'input_shape' argument
model = tf.keras.models.Sequential([tf.keras.layers.Conv2D(filters=6,kernel_size=5,padding='valid',activation='sigmoid',input_shape=(28,28,1)),tf.keras.layers.AveragePooling2D(pool_size=(2,2),strides=2,padding='valid'),tf.keras.layers.Conv2D(filters=16,kernel_size=5,padding='valid',activation='sigmoid'),tf.keras.layers.AveragePooling2D(pool_size=(2,2),strides=2,padding='valid'),tf.keras.layers.Flatten(),tf.keras.layers.Dense(120,activation='sigmoid'),tf.keras.layers.Dense(84,activation='sigmoid'),tf.keras.layers.Dense(10,activation='softmax')
])使用 model.summary() 查看模型信息。
model.summary()Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d (Conv2D) (None, 24, 24, 6) 156
average_pooling2d (AverageP (None, 12, 12, 6) 0
ooling2D)
conv2d_1 (Conv2D) (None, 8, 8, 16) 2416
average_pooling2d_1 (Averag (None, 4, 4, 16) 0
ePooling2D)
flatten (Flatten) (None, 256) 0
dense (Dense) (None, 120) 30840
dense_1 (Dense) (None, 84) 10164
dense_2 (Dense) (None, 10) 850
=================================================================
Total params: 44,426
Trainable params: 44,426
Non-trainable params: 0
_________________________________________________________________
3 模型训练
使用 compile() 函数配置模型,优化算法为 Adam 算法,学习率为 0.001,损失函数为交叉熵损失函数。
# 模型配置
model.compile(optimizer=tf.keras.optimizer.Adam(learning_rate=1e-3),loss=tf.keras.losses.CategoricalCrossentropy(),metrics=['accuracy']
)# 模型训练
model.fit(x=train_x,y=train_y,validation_split=0.0,epochs=10
)Epoch 1/10
1875/1875 [==============================] - 72s 38ms/step - loss: 0.5806 - accuracy: 0.8206
Epoch 2/10
1875/1875 [==============================] - 70s 37ms/step - loss: 0.1254 - accuracy: 0.9620
Epoch 3/10
1875/1875 [==============================] - 75s 40ms/step - loss: 0.0870 - accuracy: 0.9735
Epoch 4/10
1875/1875 [==============================] - 82s 43ms/step - loss: 0.0699 - accuracy: 0.9785
Epoch 5/10
1875/1875 [==============================] - 69s 37ms/step - loss: 0.0604 - accuracy: 0.9809
Epoch 6/10
1875/1875 [==============================] - 68s 36ms/step - loss: 0.0530 - accuracy: 0.9833
Epoch 7/10
1875/1875 [==============================] - 72s 38ms/step - loss: 0.0477 - accuracy: 0.9854
Epoch 8/10
1875/1875 [==============================] - 70s 38ms/step - loss: 0.0436 - accuracy: 0.9863
Epoch 9/10
1875/1875 [==============================] - 70s 37ms/step - loss: 0.0399 - accuracy: 0.9873
Epoch 10/10
1875/1875 [==============================] - 68s 36ms/step - loss: 0.0357 - accuracy: 0.9883
<keras.callbacks.History at 0x20a56b65660>
相关文章:

【卷积神经网络】MNIST 手写体识别
LeNet-5 是经典卷积神经网络之一,1998 年由 Yann LeCun 等人在论文 《Gradient-Based Learning Applied to Document Recognition》中提出。LeNet-5 网络使用了卷积层、池化层和全连接层,实现可以应用于手写体识别的卷积神经网络。TensorFlow 内置了 MNI…...
Ansible学习笔记2
Ansible是Python开发的自动化运维工具,集合了众多运维工具(Puppet、cfengine、chef、func、fabric)的优点,实现了批量系统配置,批量程序部署、批量运行命令等功能。 特点: 1)部署简单ÿ…...
80. 删除有序数组中的重复项 II
【中等题】 题目: 给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。 不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额…...

CVE-2023-36874 Windows错误报告服务本地权限提升漏洞分析
CVE-2023-36874 Windows错误报告服务本地权限提升漏洞分析 漏洞简介 Windows错误报告服务在提交错误报告前会创建wermgr.exe进程,而攻击者使用特殊手法欺骗系统创建伪造的wermgr.exe进程,从而以system权限执行代码。 影响版本 Windows10 1507 * Wind…...
IDEA遇到 git pull 冲突的几种解决方法
1 忽略本地修改,强制拉取远程到本地 主要是项目中的文档目录,看的时候可能多了些标注,现在远程文档更新,本地的版本已无用,可以强拉 git fetch --all git reset --hard origin/dev git pull关于commit和pull的先后顺…...
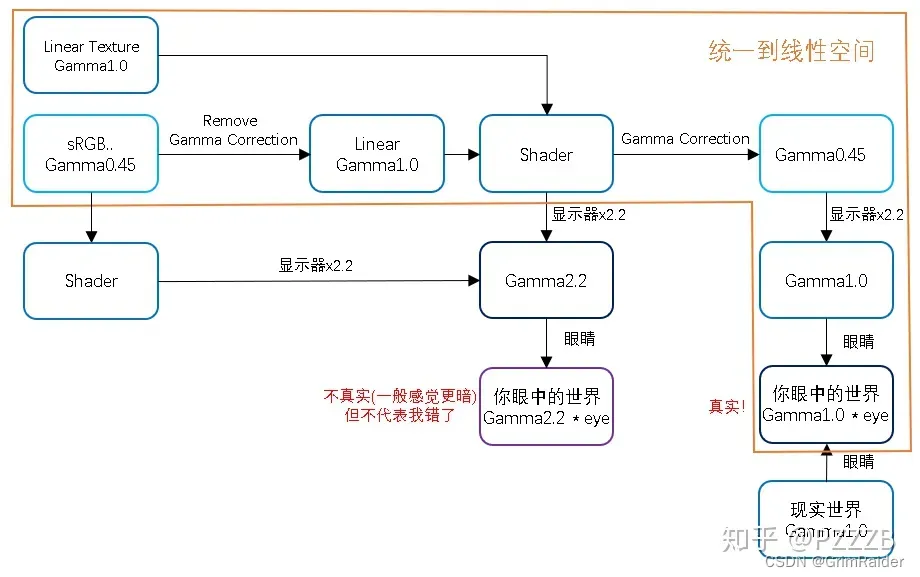
[Unity]UI和美术出图效果不一致
问题描述:美术使用PS在Gamma空间下设计的UI图,导入到Unity,因为Unity使用的是线性空间,导致半透明的UI效果和美术设计的不一致。 解决方案: (一)让美术在线性空间下工作 (二&…...

SpringBoot整合JPA和Hibernate框架
Springboot整合JPAHibernate框架【待完成】 随着MybatisPlus技术的发展,JPA和Hibernate技术已经逐步淘汰 JPA遵循了Hibernate框架规则,目前使用的不多 1、添加依赖 <!--jpa--> <dependency><groupId>org.springframework.boot</…...
,文件常用的方法)
Java中文件的创建(三种方式),文件常用的方法
文件的创建 方式1: new File(String pathName) 根据路径构建一个File对象方式2: new File(File parent,String child) 根据父目录文件子路径构建方式3: new File(String parent,String child) 根据父目录子路径构建 代码: //方…...
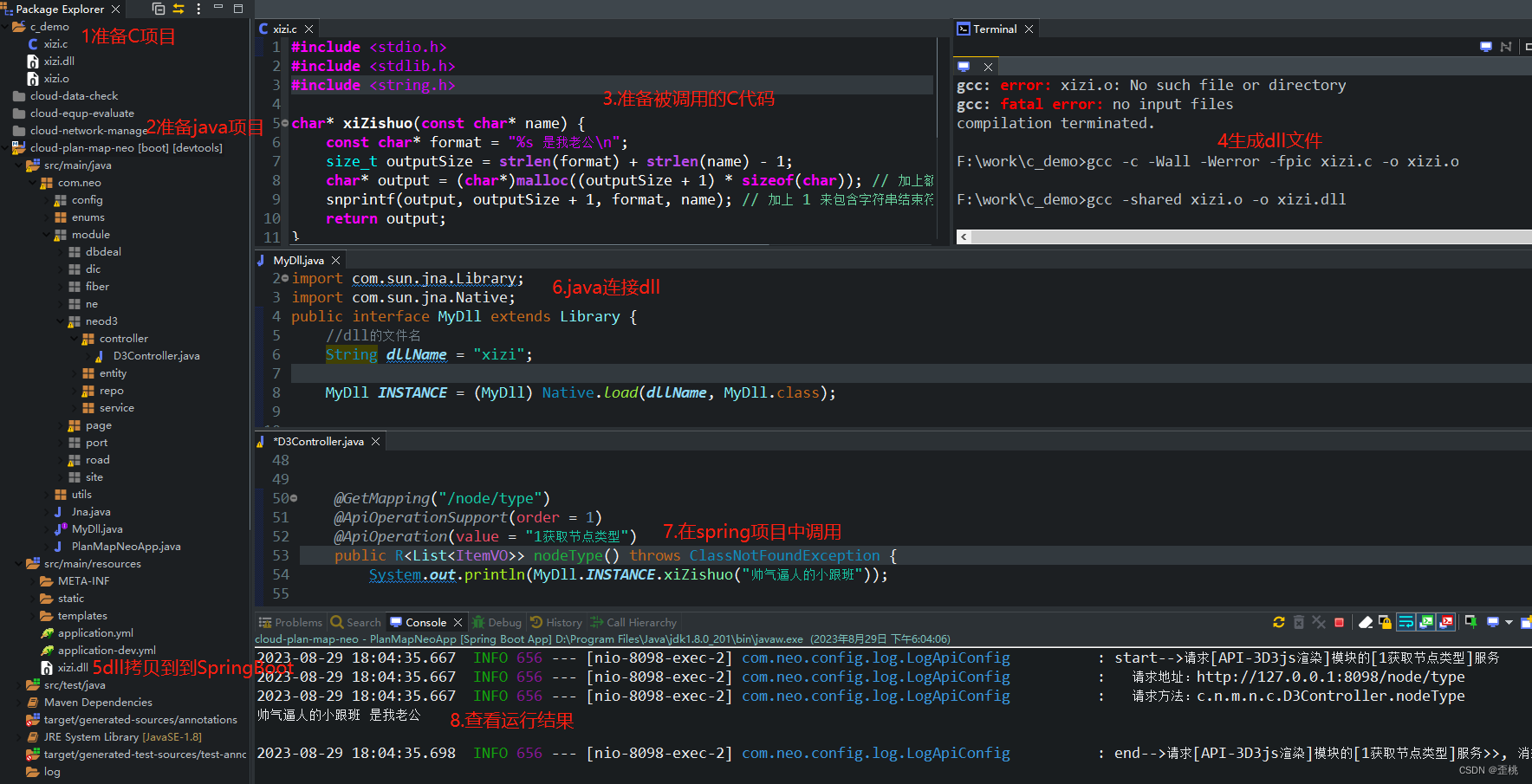
Spring boot中调用C/C++(dll)
添加JNA依赖 <dependency><groupId>net.java.dev.jna</groupId><artifactId>jna</artifactId><version>5.5.0</version> </dependency>准备C代码/C代码 如下是C代码,文件名:xizi.c #include <std…...

【Apollo学习笔记】——规划模块TASK之PATH_DECIDER
文章目录 前言PATH_DECIDER功能简介PATH_DECIDER相关配置PATH_DECIDER总体流程路径决策代码流程及框架MakeStaticObstacleDecision PATH_DECIDER相关子函数参考 前言 在Apollo星火计划学习笔记——Apollo路径规划算法原理与实践与【Apollo学习笔记】——Planning模块讲到……S…...
)
Lua学习(二)
Lua基础学习 7. lua函数8. lua运算符8.1 算数运算符8.2 关系运算符8.3 逻辑运算符8.4 其他运算符 9. lua字符串9.1 字符串格式化9.2 匹配模式 10. lua数组11. lua迭代器11.1 Lua table 12. lua 模块12.1 加载机制12.2 C 包 接着上一篇的内容。Lua学习(一)…...
制作鲜花商城小程序的详细步骤
如果你是一个新手商家,想要进入鲜花团购市场,但是不知道如何制作一个小程序商城,那么这篇文章就是为你准备的。以下是制作鲜花团购小程序商城的详细步骤: 1. 登录乔拓云平台后台,进入商城管理页面 首先,你需…...
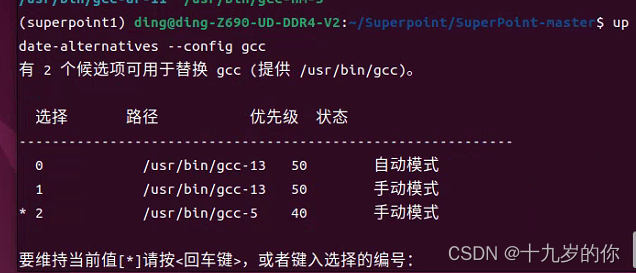
Ubuntu20以上高版本如何安装低版本GCC
安装了Ubuntu 20.04之后,通过命令行 sudo apt-get install build-essential安装gcc,再通过命令行 gcc -v可查看gcc版本为gcc13 如果想用低版本的gcc,比如gcc4.8,尝试输入命令 sudo apt-get install gcc-4.8会提示找不到gcc4.8的…...
context.WithCancel()的使用
“ WithCancel可以将一个Context包装为cancelCtx,并提供一个取消函数,调用这个取消函数,可以Cancel对应的Context Go语言context包-cancelCtx[1] 疑问 context.WithCancel()取消机制的理解[2] 父母5s钟后出门,倒计时,父母在时要学习,父母一走…...
vue3中引入百度地图
话不多说直接开干 1.第一种方式 百度地图地址 打开 https://lbsyun.baidu.com/index.php?title%E9%A6%96%E9%A1%B5 然后点进去地图 然后再这个功能里面选择一个地图,然后跳转页面 然后一直下滑 滑到底部 点击这个 跳转到这个页面 然后点击进入demo这个 然后到这个…...
【Linux-Day8- 进程替换和信号】
进程替换和信号 问题引入 我们发现 终端输入的任意命令的父进程都是bash,这是因为Linux系统是用fork()复制出子进程,然后在子进程中调用替换函数进行进程替换,实现相关命令。 (1) exec 系列替换过程:pcb 使用以前的只…...

日志文件之间关系和介绍及应用
1.常用日志框架代码举例 Log4j: Log4j是Java中广泛使用的日志框架之一。它提供了灵活的配置选项和丰富的功能,支持日志级别、日志输出目标等。Log4j有1.x版本和2.x版本,其中Log4j 2.x是对1.x的升级和扩展。 Logback: Logback是由Log4j创始人设计的Log4…...
mac电脑屏幕录制Berrycast Mac屏幕录制软件
Berrycast是一款为Mac设计的优秀屏幕录制软件,它让屏幕录制变得简单而高效。以下是Berrycast的一些主要特点: 简单的用户界面:Berrycast拥有直观和简洁的用户界面,使得用户可以轻松上手。高质量的视频输出:Berrycast能…...
最优化问题概述)
机器学习笔记之最优化理论与方法(一)最优化问题概述
机器学习笔记之最优化理论与方法——最优化问题概述 引言什么是最优化问题最优化问题的基本形式最优化问题的分类各分类最优化问题的数学表达约束优化VS无约束优化线性规划VS非线性规划连续优化VS离散优化单目标优化VS多目标优化 引言 从本节开始,将对最优化理论与…...

【ES5新特性一】 严格模式语法变化、全局的JSON对象、编码和解码的方法
前言 ECMAScript 和 JavaScript 的关系 一个常见的问题是,ECMAScript 和 JavaScript 到底是什么关系? 要讲清楚这个问题,需要回顾历史。1996 年 11 月,JavaScript 的创造者 Netscape 公司,决定将 JavaScript 提交给标准…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
